2. 新疆水文水资源工程技术研究中心, 乌鲁木齐 830052;
3. 新疆水利工程安全与水灾害防治重点实验室, 乌鲁木齐 830052
2. Xinjiang Hydrology and Water Resources Engineering Research Center, Urumqi 830052, China;
3. Xinjiang Key Laboratory of Hydraulic Engineering Security and Water Disasters Prevention, Urumqi 830052, China
近年来因不合理采矿、季节性强化施肥、干旱和半干旱地区地下水资源超采等造成的硫酸盐(SO42-)污染问题愈加严重, 严重威胁当地生态平衡和居民健康[1 ~ 3]. 准确可靠预测地下水SO42-空间分布可以有效减少地区地下水水质监测所需的经济成本和人力负担, 对评估与SO42-有关的健康风险和实施劣质饮用水防控计划至关重要[4]. 高SO42-地下水形成是一个复杂的过程, 中间涉及非常多的物理、化学和生物作用, 其形成过程可以看作是一定时间尺度下多种因素共同作用的结果, 地理环境[1]、人类活动[5]和土壤条件[6]等都是对其进行空间分布预测时需要考虑的因素. 遥感技术可以将上述影响因素进行量化, 为空间预测模型提供数据基础[7]. 土地覆盖类型在遥感数据中常被用于研究人类活动影响地下水水化学组分空间变化的环境因子, 例如选取区域内农业和城市等土地覆盖类型面积占比作为特征变量结合不同模型预测地下水水化学组分空间变化情况[8 ~ 10]. 数字高程数据(如地形、距河流距离等)[8, 11, 12]和土壤参数数据(如土壤pH值、有机碳)[8, 10, 12]在空间分布预测中也经常被用作影响地下水水化学组分浓度变化的环境因子. 近年来遥感技术的快速发展为机器学习模型提供了丰富的数据资源, 机器学习模型作为数据驱动模型不需要对高SO42-地下水形成过程建模, 对于数据本身的质量要求较低, 可直接挖掘目标与环境因子间的数据关系, 在模拟复杂地下水环境方面更加精确[4, 13], 并且已在砷[14]、氟[15]、碘[16]和硝酸盐[8, 9, 11]等劣质地下水空间分布预测建模中做了较多的研究, 但对于地下水SO42-空间分布预测建模的研究相对较少. 此外, 其在新疆地区的适用性上也有较好的表现, 已有针对天山北坡地下水储量预测[17]和塔里木河流域地下水水位预测[18]的研究, 但在区域内劣质地下水空间分布预测方面尚存在空白.
随机森林(random forests, RF)是一种基于机器学习模型的统计算法, 它能综合多源数据进行预测并且结果具有较高的准确率, 其在劣质地下水空间分布预测建模中已有广泛的应用, 但绝大多数研究在建模过程中并未明确提出模型的超参数, 这是地下水水质建模的重要挑战之一[19]. 超参数是影响机器学习模型预测性能的重要因素之一, 需要在模型训练前进行设置. 贝叶斯优化算法(bayesian optimization algorithm, BOA)是一种高效的智能优化算法, 可以结合实际问题对模型超参数进行优化, 能更加快速、准确地获得问题的最优解[20]. Alibrahim等[21]通过对比网格搜索、贝叶斯优化和遗传算法等3种超参数优化方法对模型性能的提升效果得出贝叶斯优化算法有较好的准确度和运算速度. Sun等[22]利用贝叶斯优化算法分别结合逻辑回归和随机森林对滑坡发生情况建模, 结果表明贝叶斯优化算法对随机森林有着很好的优化效果. 因此, 贝叶斯优化算法在耦合超参数和模型的相互关系, 获得更加精确的空间分布预测结果等方面具有较好的潜力.
地下水流场是影响地下水SO42-迁移的重要因素, 但大尺度区域无法完全掌握地下水流场的变化[9], 因此必须采用简化手段量化取样点的汇水区. 新疆叶尔羌河流域受地形影响, 区域内地下水流向总体呈现出自西南向东北流动的特点[23], 按此特点将取样点汇水方向曲线流型区域设为贡献区, 以贡献区内各土地覆盖类型的面积占比作为人类活动的影响因子, 可以更好地量化土地覆盖类型对地下水参数的影响;其次为弥补每年取样点分布不均、数量不足的缺点, 设计将研究区网格化, 利用地统计插值对单一变量的空间分布预测有较好性能的特点[24], 对每年地下水水质参数数据和环境因子进行插值并提取到网格中心点, 将网格中心点作为辅助样本输入到模型当中. 综上, 本文以新疆叶尔羌河流域平原区为研究区域, 拟通过探索分析研究区多年的土地覆盖数据、土壤参数数据、数字高程数据、地下水pH值与地下水SO42-浓度的相关性, 利用BOA优化随机森林中回归算法(random forests regression, RFR)超参数, 建立融合多源时空数据的地下水SO42-空间分布预测模型, 确定未来高SO42-地下水区域, 减少地下水水质指标监测质量控制所需人力和时间成本, 以期为当地确定地下水改良区域和地下水安全供应提供参考.
1 材料与方法 1.1 研究区概况叶尔羌河流域地理位置介于76°38′~80°45′E, 37°22′~40°29′N, 北临天山山脉, 南靠昆仑山, 西依帕米尔高原, 东接塔克拉玛干沙漠. 流域包括叶尔羌河、提孜那甫河、柯克亚河和乌鲁克河等4条河流, 多年平均径流量为7.58 × 109 m3. 该流域可划分为南部山区和北部平原区, 南部山区主要由元古界、古生界和中生界的变质岩、石灰岩、砂岩、泥岩及砂砾岩组成[25], 北部平原区主要分布第四系冲洪积扇和冲(湖)积平原, 沉积物颗粒由南至北逐渐变细变薄, 厚度为100~300 m[26].
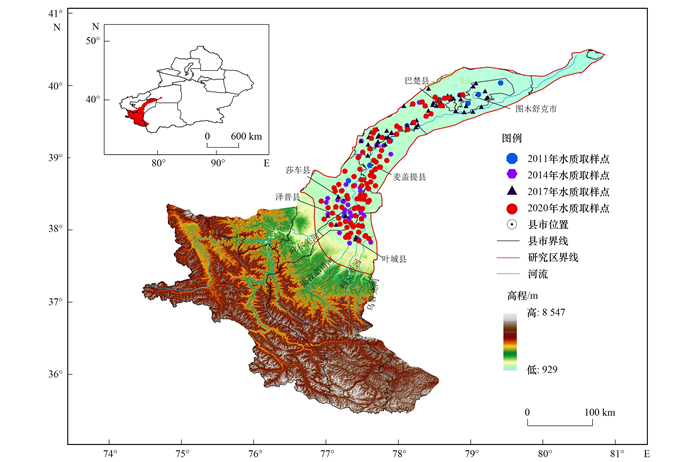
该区域属于典型的温带大陆性干旱气候, 平均气温11.9℃, 年平均降水量52.7 mm, 年平均蒸发量2 454 mm[27]. 平原区的地下水补给主要来源于地表水入渗和山前含水层侧向补给[16], 蒸发、泉排和人为抽取则是该区域地下水的主要排泄方式, 地下水流向与叶尔羌河流向一致, 即自西南向东北流动(见图 1)[23].
|
图 1 研究区位置与地下水取样点分布示意 Fig. 1 Location of the study area and groundwater sampling sites |
本研究需要的数据包括2011、2014、2017和2020年叶尔羌河流域平原区的土地覆盖数据、土壤参数数据、数字高程数据、地下水水化学参数数据(pH值和SO42-浓度). 所有数据利用地下水监测井空间分布数据进行掩膜, 并叠加叶尔羌河流域平原区界线, 经栅格计算, 获得每个监测井的变量值.
1.2.1 土地覆盖数据本研究利用中国年度土地覆盖数据集[28], 提取出耕地(arable land, ARA)、荒地(bare land, BAR)和草地(green land, GRE)等3种土地覆盖(land cover, LC)类型作为预测模型的特征变量.
为了量化LC类型并分析其对地下水SO42-浓度的影响, 需要确定取样点的贡献区(contributing area, CA). 贡献区的定义为相对于一口井的区域, LC类型对一口井中地下水质量有显著影响[29]. 前人提出了很多方法来确定井的贡献区, 例如圆形[30]、半圆形[31]、扇形[9]和探照灯型[32]等, 然而, 以上方法有的忽略了含水层水流流动方向的影响, 有的仅考虑地下水渗流场中存在直流线的情况. 在本研究中, 考虑到地下水系统的流线是典型的曲线, 故采用曲线流形[29]来确定研究区采样点和网格点的贡献区面积. 根据He等[29]的研究结论, 按地下水汇水方向将贡献区的长度和宽度分别设定为750 m和500 m, 然后计算每个LC类型在取样点的贡献区面积中的占比, 以此作为该LC类型在训练集和测试集中的特征变量.
1.2.2 土壤参数数据本研究采用中国寒区旱区科学数据中心网站(http://data.casnw.net/portal/)下载的基于世界土壤数据库(HWSD)(V1.1)的中国土壤数据集. 土壤数据库由表土和底土两层组成, 分别代表上部和下部土壤. 分别选取表土和底土中的容重(topsoil/subsoil bulk density, TBD/SBD)、有机碳(topsoil/subsoil organic carbon, TOC/SOC)、pH(H2O)[topsoil/subsoil pH(H2O), TpH/SpH]、CaSO4(topsoil/subsoil calcium sulfate, TCAS/SCAS)和盐分(topsoil/subsoil salinity, TECE/SECE)等5种土壤参数作为预测模型特征变量.
1.2.3 数字高程数据来源于“地理空间数据云(http://www.gscloud.cn/)”提供的“ASTER GDEM”数据集, 栅格尺寸为30 m × 30 m. 从数据集中提取出监测井的地面高程(ground elevation, GE), 并计算监测井的地表坡度(ground surface slope, GSS)及距叶尔羌河距离(distance to the Yarkant River, DISY), 将以上3种地理信息参数为预测模型特征变量.
1.2.4 地下水水化学参数数据本研究已获取叶尔羌河流域平原区2011年19组、2014年53组、2017年89组和2020年33组的地下水水质检测数据(图 1), 包含地下水pH值(作为预测模型的特征变量)和SO42-浓度(作为预测模型的响应变量)等. 为保证地下水取样点的代表性, 其均来自当地居民生活用水和灌溉用水井, 取样时间为每年的6~8月.
1.3 研究方法 1.3.1 贝叶斯优化算法(BOA)贝叶斯优化算法(BOA)被广泛用于确定模型的最优超参数值, 其能够快速获得最优值[33]. 贝叶斯定理是贝叶斯优化算法的基础, 其表达式为:
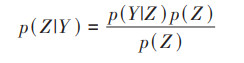
|
(1) |
式中, p(Z|Y)表示Z在给定Y条件下的后验概率分布;p(Y|Z)表示Y在给定Z条件下的似然概率分布;p(Z)表示Z的先验概率分布;p(Y)表示边际化Z的边际似然概率分布[20].
BOA由概率代理模型(probabilistic surrogate model, PSM)和采集函数(acquisition function, ACF)组成, 式中Z表示概率代理模型, p(Z|Y)表示采集函数. BOA是一种交互式算法, 通过不断迭代, PSM拟合目标函数并寻找最优解, 高斯过程(gaussian processes, GP)是应用最为广泛的PSM. GP作为代理黑箱函数时, 能够仅通过一致连续或利普希茨连续(Lipschitzcontinuity)等局部平滑假设, 即可得到满意结果, 局部平滑性等弱假设更符合实际问题, 并且能够使贝叶斯优化有效地利用局部邻近信息进行更准确地判断, 从而更准确地选择最优解[20].
1.3.2 随机森林回归(RFR)随机森林是Breiman于2001年提出的一种集成机器学习算法, 用来克服使用单一决策树时过拟合和不稳定的缺点[34]. 其基本概念是在原始训练数据集的随机子集上独立构建多个决策树, 通过这些独立决策树预测的平均值提高算法的泛化能力和鲁棒性[35].
将各年份的特征变量数据和地下水SO42-浓度数据进行集成, 共同构成BOA-RFR模型的样本数据集. 为了生成更大尺寸的RF训练集和测试集, 同时弥补每年取样点分布不均、数量不足的缺点, 将研究区网格化, 网格单元大小2 km, 运用ArcGIS地统计插值功能, 将特征变量(3个环境因子中的16个变量和地下水pH值)和响应变量(地下水SO42-浓度)赋值到网格中心点, 作为辅助样本, 实测样本与辅助样本共同组成BOA-RFR模型原始样本集.
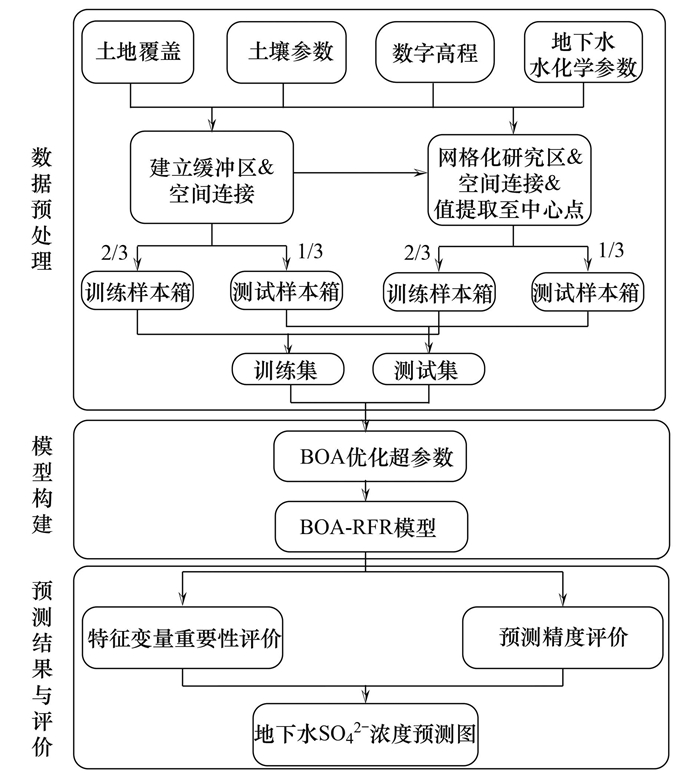
为确保实测样本和辅助样本合理分布在BOA-RFR模型的训练集和测试集中, 设计以下抽样程序:设置两个样本箱, 分别为训练样本箱和测试样本箱. 将每年的实测样本和辅助样本均随机分为两部分, 其中2/3放入训练样本箱, 1/3放入测试样本箱, 将实测样本和辅助样本的训练样本箱和测试样本箱分别合并, 组成新的训练集和测试集. 本文构建地下水SO42-预测模型流程如图 2所示.
|
图 2 模型设计流程 Fig. 2 Flow of model designs |
土地覆盖、土壤参数和数字高程等时空数据值的提取均由ArcGIS 10.8实现, 运用Python 3.10语言中1.1.2版本的Scikit-learn包实现RFR.
1.3.3 特征变量重要度评价RFR可以对多个特征变量进行变量重要度分析、奇异值检测等[36], 能够分析其对响应变量的影响. 通过BOA-RFR模型对特征变量的重要度进行评价, 分析不同环境因子对地下水SO42-浓度的影响程度. 其通过加入噪声影响, 通过袋外样本(out of bag, OOB)计算模型准确度降低程度, 直接评价每种特征变量对模型预测准确率的影响, 模型特征变量重要度计算公式为:
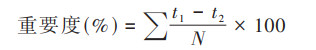
|
(2) |
式中, t1表示RFR中每棵决策树的OOB误差;t2表示添加噪声干扰后, 随即改变样本值得出的OOB误差;N表示RFR中决策树棵树[36]. 某个特征变量因随机加入噪声影响后, OOB误差大幅度降低, 则说明这个特征变量重要度较高, 对模型预测结果具有较大影响.
1.3.4 模型预测精度评价采用地下水SO42-浓度实测值和预测值之间的平均绝对误差(MAE)、均方根误差(RMSE)和决定系数(R2)等3个机器学习模型回归预测常用度量评估模型性能[9], 各指标的计算公式如下:
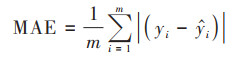
|
(3) |
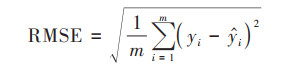
|
(4) |
式中, yi和
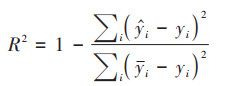
|
(5) |
式中, 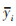
R2评价模型拟合能力, MAE和RMASE评价模型预测值和实测值离散程度. R2越接近1, 模型的拟合优度越高;MAE和RMSE越接近于0, 模型的预测精度越高.
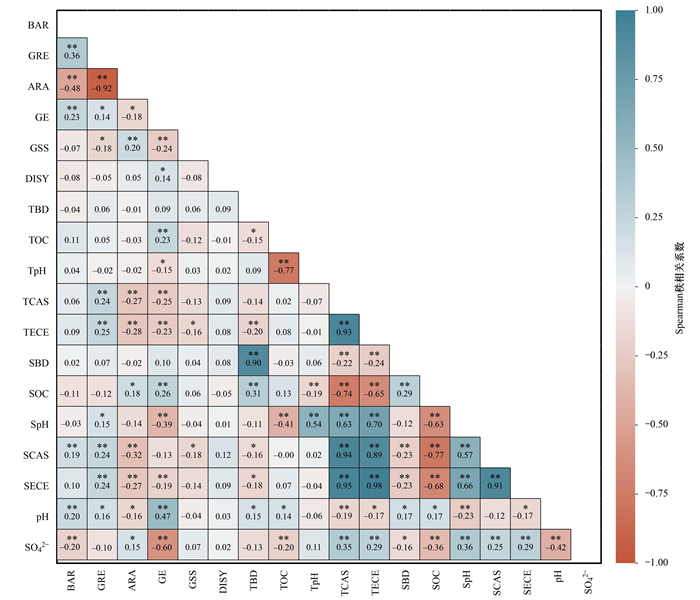
2 结果与分析 2.1 特征变量相关性分析用于模型预测的特征变量多为非正态分布、具有相关离散值的数据, 故采用Spearman秩相关系数法研究特征变量与地下水SO42-浓度之间的关系[37](图 3), 结果表明地下水SO42-浓度与特征变量间均存在着不同程度的相关性. 土地覆盖数据中, 地下水SO42-浓度与BAR呈极显著负相关(r = -0.20), 与ARA呈显著正相关(r = 0.15), 与GRE无相关性;数字高程数据中, 仅GE与地下水SO42-浓度为极显著负相关(r = -0.60), GSS和DISY均无相关性;土壤参数数据中, TCAS、TECE、SpH、SCAS和SECE与地下水SO42-浓度呈极显著正相关, r分别为0.35、0.29、0.36、0.25和0.29, TOC和SOC与之呈极显著负相关, r分别为-0.20和-0.36, SBD与之呈显著负相关(r = -0.16), 而TBD和TpH均无明显相关性. pH值作为影响地下水理化性质的重要因素, 与地下水SO42-浓度呈极显著负相关(r = -0.42). 总体上, 土地覆盖数据、土壤参数数据和数字高程数据均有与地下水SO42-浓度存在相关性的参数, 3种时空数据均对地下水SO42-浓度有一定程度影响.
|
*表示P≤0.05, 为显著;**表示P≤0.01, 为极显著 图 3 特征变量与地下水SO42-浓度相关性分析 Fig. 3 Correlation analysis between characteristic variables and groundwater SO42- concentration |
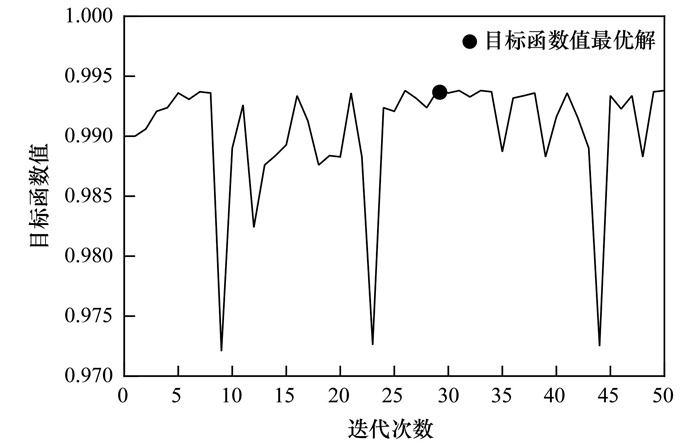
利用Python 3.10语言中1.3.1版本的Bayesian-optimization包实现BOA算法, 对王焰新等[19]提出的决策树的最大深度、拆分内部节点所需的最少样本数和决策树棵树等RFR算法的3个核心超参数进行优化(表 1);随即状态值(random_state)设为定值, 其余参数设为默认值, 通过5折交叉验证确定BOA算法优化结果. 通过多次验证迭代次数, 最优解一般在50次以内, 故设置迭代次数为50. BOA在运行过程中主动寻优, 每次仅产生一个样本点, 且依靠代理模型产生下一个样本点, 故收敛过程呈波动状态(图 4). BOA在第29次迭代确定采集函数最优相关系数为0.993 8, 此时的max_depth、min_samples_split和n_estimators等3个超参数值分别为35.0、2.6和239, 总运行时间为3 174 s. BOA较短时间内就可找到模型的最优超参数, 极大减少了模型调参所需时间, 提高了模型构建效率.
|
|
表 1 RFR参数空间范围 Table 1 Space range of parameters of random forest regression |
|
图 4 模型优化过程中BOA算法的最优目标函数值 Fig. 4 Optimal objective function value of the BOA in the process of optimizing models |
利用BOA-RFR模型计算特征变量的重要性, 按照模型准确率降低程度对特征变量进行量化, 综合考虑4年特征变量对模型准确率降低程度由大到小排序(图 5). 结果表明, pH值、GE和BAR对地下水SO42-浓度的重要性远大于其他因素, 重要度均超过25%, 说明除了地下水本身的理化性质外, 地形和人类活动对地下水SO42-浓度的影响也非常大. 其次是土壤参数SBD, 重要度为12.87%, 说明土壤也是影响地下水SO42-浓度的重要环境因子. 其余环境因子参数均对地下水SO42-浓度重要度较低, 重要度均小于4%.

|
图 5 特征变量重要度排序 Fig. 5 Importance ranking chart of characteristic variables |
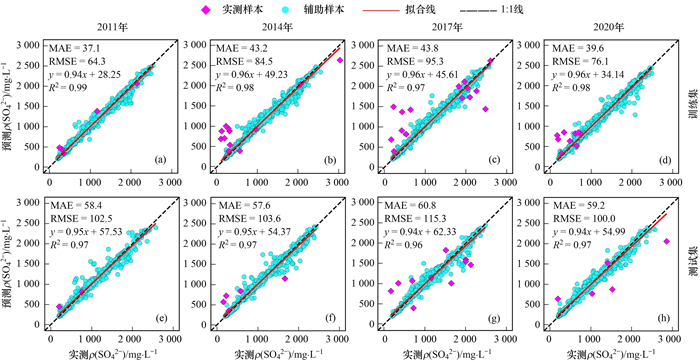
基于4 a的训练集和测试集样本分别构建BOA-RFR模型, 其中训练集样本和测试集样本分别为总样本数的2/3和1/3(图 6). 由图 6可知, 基于4年训练集和测试集样本构建的BOA-RFR模型的拟合优度均较高, R2均为0.96以上. 其中基于训练集数据建模的BOA-RFR模型预测精度较高, RMSE分别为64.3、84.5、95.3和76.1 mg·L-1, MAE分别为37.1、43.2、43.8和39.6 mg·L-1, 对比基于测试集样本构建的BOA-RFR模型, RMSE分别减小了38.2、19.1、20.0和23.9 mg·L-1, MAE分别减小了21.3、14.4、17.0和19.6 mg·L-1, 训练集加入了更多的地统计插值样本为BOA-RFR模型提供了更多的学习材料, 提高了预测精度. 对比4年数据分别构建的BOA-RFR模型, 2011年和2020年的预测精度要优于2014年和2017年, 这可能是因为2014年与2017年的实测样本数据值离散程度大于2011年与2020年实测样本. 因此, 当研究区取样困难、模型无法通过现有样本输出理想效果时, 地统计插值方法可以作为辅助手段, 通过对现有样本进行插值预测生成辅助样本, 增加训练样本数以提高模型的预测精度, 一定程度上可弥补数据本身存在的不足, 获得更好的预测结果.
|
图 6 2011、2014、2017和2020年基于训练集和测试集BOA-RFR建模结果对比 Fig. 6 Comparison of BOA-RFR modeling results based on training set and test set in 2011, 2014, 2017, and 2020 |
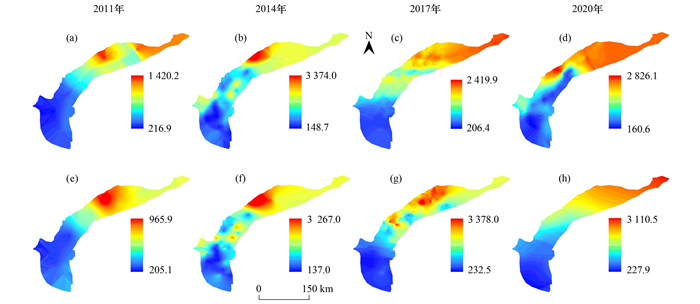
使用BOA-RFR模型分别对4年的地下水SO42-浓度进行预测, 并与实测的地下水SO42-浓度图进行对比(图 7). 2011年和2014年高浓度地下水SO42-区域有一定程度的压缩, 但预测的最大值、最小值均增大, 实测样本高值点集中分布于研究区东北部, 其余地区高值点零星分布, 因为在建模过程中使用了地统计插值方法生成的辅助样本, 且2011年和2014年75%地下水样本ρ(SO42-)均小于2000 mg·L-1(图 8), 高浓度SO42-样本的缺少致使插值过程中高浓度地下水SO42-区域受到周边低浓度地下水SO42-影响, 降低了模型的预测性能, 所以高浓度地下水SO42-预测区域减小, He等[8]的研究中也出现了类似的偏差. 2017年和2020年高浓度地下水SO42-区域变化情况, 预测结果较为相似, 呈现出西南部区域减小, 东北部区域增多, 向地势趋于平缓, 人口密度较大的平原区东北部富集趋势. 2017年和2020年预测的地下水ρ(SO42-)最大值分别为2 419.9 mg·L-1和2 826.1 mg·L-1, 最小值分别为206.4 mg·L-1和160.6 mg·L-1, 比实测样本的最大值分别减小了958.1 mg·L-1和284.4 mg·L-1, 最小值分别减小了26.1 mg·L-1和67.3 mg·L-1. 一方面可能由于灌溉过程中, 低浓度SO42-地表水入渗补给地下水, 造成地下水SO42-降低[38], 但模型缺少地表水灌溉水量等方面的特征变量, 导致预测产生误差. 另一方面每年地下水SO42-浓度样本分布也影响了模型预测精度, 从训练集和测试集地下水SO42-浓度直方图和箱线图可以看出(图 8), 研究区0~1 500 mg·L-1的SO42-样本数量较多, 2017年和2020年地下水SO42-样本最大值对比2014年减小, 且2017年训练集与测试集地下水SO42-样本最大值有较大偏差, 2020年地下水SO42-浓度值中位线对比2014年减小. 从降水输入角度分析, 根据美国国家海洋和大气管理局(https://www.noaa.gov/)公布的气象数据计算得出, 研究区2011、2014、2017和2020年的年总降水量分别为21、21、20和36 mm, 设计时间尺度的年总降水量均较小, 且变化量最大为16 mm, 所以基本排除降水输入SO42-的影响.
|
(a)~(d)为SO42-浓度预测值, (e)~(h)为SO42-浓度实测值;色柱表示浓度, 单位为mg·L-1 图 7 2011、2014、2017和2020年地下水SO42-浓度实测与预测空间分布对比 Fig. 7 Spatial distribution of measured and projected groundwater SO42- concentrations in 2011, 2014, 2017, and 2020 |

|
(a)训练集和测试集地下水SO42-浓度分布区间, (b)2011、2014、2017和2020年地下水SO42-浓度箱线图 图 8 2011、2014、2017和2020年地下水SO42-浓度分布 Fig. 8 Distribution of groundwater SO42- concentrations in 2011, 2014, 2017, and 2020 |
由于受到环境因素与人类活动的影响, 地下水SO42-浓度预测存在一定的不确定性, 因此在考虑地下水SO42-浓度与影响因子之间关系的基础上, 探讨不同预测模型及改进优化方法在环境复杂区域地下水SO42-预测的适用性, 对提高地下水SO42-浓度预测精度, 绘制更加精准的预测图, 对当地有关部门更加高效的地下水资源应用于管理具有重要意义.
3.1 环境因子的有效性本研究选取的部分环境因子与地下水SO42-浓度具有一定程度的相关性. 对于数字高程数据来说, 地表高程(GE)与地下水SO42-浓度呈强负相关, 叶尔羌河流域山地丘陵区天然状态下地下水ρ(SO42-)环境背景值最低, 最大为464.5 mg·L-1, 而作为研究区的平原区, 环境背景值最大为1 422.5 mg·L-1, 远超过《地下水质量标准》(GB/ T 14848-2017)Ⅲ类限值[39], 并且模型输入取样点最大高程差为337 m, 地表高程的变化会引起地下水流场和地下水溶质运移过程发生变化[40], 导致地下水SO42-富集. 一方面是地下水流动过程中矿物溶解并携带SO42-从山区聚集到平原区[41], 另一方面是南部山区的地下水补给区和山前冲洪积平原的地下水径流区地下水流动条件好、蒸发排泄作用相对较小, 导致地下水SO42-含量较低;研究区北部的冲湖积平原排泄区, 地下水径流滞缓, 蒸发盐岩的溶解较剧烈, 地下水SO42-含量升高[42]. 叶尔羌河附近地下水会受到河流入渗补给的影响, 但是在本研究区域距叶尔羌河距离(DISY)、地表坡度(GSS)与地下水SO42-浓度没有相关性, 这可能是因为研究区地处平原区, 地表变化较小, 地表水无法长距离影响地下水, 且叶尔羌河下游径流量大幅度减少, 地表水入渗减少, 平原区采用地表水和地下水混合用水方式, 一定程度上减小了地表水对地下水SO42-浓度的影响[43]. 但GSS和DISY参数可以作为辅助环境因子优化地下水SO42-浓度预测模型, 减少特殊地理环境对模型精度的影响.
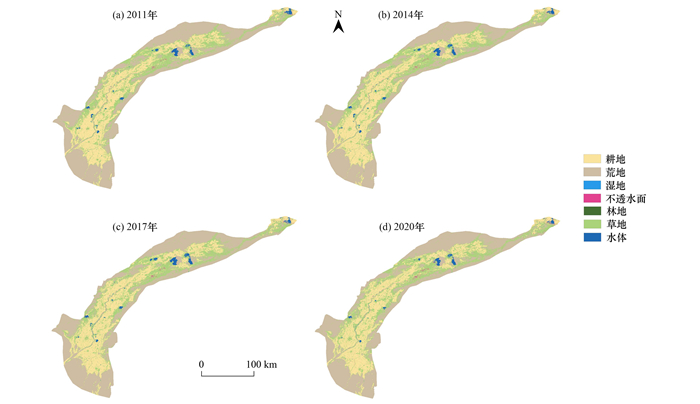
有研究表明, 农业化肥的过量施用是造成地下水SO42-污染的重要原因之一[5, 44, 45], 相关性分析结果表明, ARA与地下水SO42-浓度表现为显著正相关, 这与前人研究结果相同. BAR与地下水SO42-浓度表现为极显著负相关, 主要原因是荒地人类活动较弱, 对地下水扰动作用小, 荒地的大面积占比有效减少了地下水中SO42-的输入. 从遥感影像中提取研究区LC类型进行分析(图 9), 结果表明研究区主要的土地覆盖类型为荒地和耕地, 2011年和2020年荒地面积在叶尔羌河流域平原区面积占比分别46.1%和45.2%, 耕地面积占比分别为27.7%和28.5%, 土地覆盖参数面积占比变化较小, 但荒地的大面积占比使其对模型的预测效果影响较大, 而耕地面积占比较小对模型预测效果影响也较小. 土地利用参数可以在一定程度上优化研究区地下水SO42-高值区域的预测效果, 为模型提供更加丰富的学习经验.
|
图 9 研究区2011、2014、2017和2020年土地覆盖类型 Fig. 9 Land cover patterns in 2011, 2014, 2017, and 2020 |
土壤是地表水、生活污水和大气降水等因素影响地下水水质的媒介, 土壤中的有机硫降解和矿化也是地下水中SO42-的重要来源之一[6]. 对于土壤参数来说, TCAS和SpH与地下水SO42-浓度呈中等正相关. 这表明碱性土壤和高硫酸钙含量有助于地下水SO42-富集. 一方面SO42-是土壤盐碱化过程的主要溶质指示物, 大量蒸发盐岩风化致使土壤碱性增强, 灌溉用水、降水和生活污水会携带蒸发盐和土壤硫酸钙进入地下水, 导致地下水SO42-浓度升高[46, 47];另一方面地下水水位变动, 影响SO42-在土壤剖面上的纵向迁移, 使之向地下水中富集[48]. SOC与地下水SO42-浓度呈中等负相关, 可能是由于有机碳是良好的吸附剂, 吸附了部分流经土壤的SO42-[49].
pH值是地下水重要的指标, 影响蒸发盐岩溶解和生物有效性. 相关性分析结果表明, 地下水pH值与地下水SO42-浓度呈中等负相关, 原因可能是叶尔羌河流域平原区浅层地下水pH值变化范围为6.85~8.60, 含SO42-矿物在溶解过程中降低了地下水pH值, 酸性或弱碱性的地下水环境表明含SO42-矿物溶解作用强, 导致地下水SO42-浓度升高;随着碱性增强, 含SO42-矿物溶解作用减弱, 地下水SO42-浓度降低[47].
本研究考虑的影响因子仍有一定的局限性, 可在后续的研究中增加更多环境因子, 有研究将地质、地下水位、气象数据、Ca2+和Mg2+等因素作为优化模型的协变量[50 ~ 52], 并且取得了不错的预测精度, 如Yesilnacar等[53]的研究利用地下水水位和Ca2+等因子构建人工神经网络预测地下水SO42-浓度, 结果表明模型预测精度好且稳定性高;Lischeid[54]的研究选取空气温度和融雪指标作为辅助变量, 采用人工神经网络模型预测径流内SO42-变化趋势, 结果表明上述气象因子对模型的优化效果较好.
3.2 预测精度分析相比手工搜索、网格搜索和随机搜索, 贝叶斯优化有着更好的性能, 极大地提高了模型的运算效率和预测精度, 不同优化算法对模型性能有着不同的影响, 后期研究将对比遗传算法、贝叶斯优化算法和网格搜索等在随机森林算法优化方面的优缺点, 设计出更加适合模型的优化算法[21, 22, 55].
本研究中受到了一些不确定性的困扰, 其中一个问题是LC类型粗糙的时空分辨率和较少的分类, 可能无法真实地反映人类活动对于地下水SO42-浓度的影响[56, 57]. 特别是LC类型中缺少建筑用地类型, 没有生活污水对地下水SO42-浓度的影响进行量化, 导致在县市周围地下水SO42-浓度预测图精度出现不同程度下降, 因此, 如果要提高遥感数据在地下水水质预测中的作用, 高分辨率时空连续数据是非常重要的;另一个问题是地下水SO42-监测井位置大部分位于平原区东北部, 南部山区数量较少, 导致2011年和2014年地下水SO42-浓度预测图在研究区西南部预测精度下降, 所以科学布设监测井对于地下水SO42-预测同样重要.
随机森林在预测地下水水化学组分变化上具有很大的潜力, 但其他算法在地下水水化学组分预测方面也有优势, 后期研究将对比神经网络、逻辑回归等机器学习算法在地下水水化学组分预测的优缺点, 解决算法对于人类活动和多变气候等多源条件下的适用性[51, 58, 59].
4 结论(1) pH值、GE和BAR作为影响地下水水化学组分的重要参数, 其与地下水SO42-浓度均呈现极显著负相关, 在地下水SO42-浓度预测特征变量重要性分析中, 重要性远大于其他因子, 重要度均大于25%, 而土壤参数的重要性相对较低, 重要度均低于15%.
(2) 添加地统计插值样本的BOA-RFR模型, 提升了模型构建效率及预测精度, 模型的R2均为0.96以上. 利用训练集样本构建的BOA-RFR模型RMSE最大值为95.3 mg·L-1, MAE最大值为43.8 mg·L-1, 较基于测试集样本构建的BOA-RFR模型相同评价指标的最小值分别降低了4.7%和23.8%, 表明地统计插值方法可以作为空间分布预测建模的辅助方法, 其生成的辅助样本可以一定程度上弥补数据本身存在的不足, 增加模型预测精度.
(3) 基于BOA-RFR模型生成地下水SO42-浓度预测图, 预测图表明, 高SO42-地下水主要集中于叶尔羌河流域平原区东北部, 且面积呈扩大趋势, 2017年和2020年预测的地下水SO42-浓度最大值最小值均有所减小, 但高SO42-浓度区域扩大, 对比实测样本的最大值分别减小了958.1 mg·L-1和284.4 mg·L-1, 最小值分别减小了26.1 mg·L-1和67.3 mg·L-1. 地下水SO42-浓度预测图可为确定需要进行地下水监测和改良的地区提供参考.
| [1] | Zak D, Hupfer M, Cabezas A, et al. Sulphate in freshwater ecosystems: A review of sources, biogeochemical cycles, ecotoxicological effects and bioremediation[J]. Earth-Science Reviews, 2021, 212. DOI:10.1016/j.earscirev.2020.103446 |
| [2] | Kinnunen P, Kyllönen H, Kaartinen T, et al. Sulphate removal from mine water with chemical, biological and membrane technologies[J]. Water Science and Technology, 2018(1): 2017-205. |
| [3] | Zhang J, Jin M G, Cao M D, et al. Sources and behaviors of dissolved sulfate in the Jinan karst spring catchment in northern China identified by using environmental stable isotopes and a Bayesian isotope-mixing model[J]. Applied Geochemistry, 2021, 134. DOI:10.1016/j.apgeochem.2021.105109 |
| [4] | Haggerty R, Sun J X, Yu H F, et al. Application of machine learning in groundwater quality modeling–a comprehensive review[J]. Water Research, 2023, 233. DOI:10.1016/j.watres.2023.119745 |
| [5] | Torres-Martínez J A, Mora A, Knappett P S K, et al. Tracking nitrate and sulfate sources in groundwater of an urbanized valley using a multi-tracer approach combined with a Bayesian isotope mixing model[J]. Water Research, 2020, 182. DOI:10.1016/j.watres.2020.115962 |
| [6] | Zhang D, Li X D, Zhao Z Q, et al. Using dual isotopic data to track the sources and behaviors of dissolved sulfate in the western North China Plain[J]. Applied Geochemistry, 2015, 52: 43-56. DOI:10.1016/j.apgeochem.2014.11.011 |
| [7] | Das M, Ghosh S K. Data-driven approaches for spatio-temporal analysis: a survey of the state-of-the-arts[J]. Journal of Computer Science and Technology, 2020, 35(3): 665-696. DOI:10.1007/s11390-020-9349-0 |
| [8] | He S, Wu J H, Wang D, et al. Predictive modeling of groundwater nitrate pollution and evaluating its main impact factors using random forest[J]. Chemosphere, 2022, 290. DOI:10.1016/j.chemosphere.2021.133388 |
| [9] | Knoll L, Breuer L, Bach M. Large scale prediction of groundwater nitrate concentrations from spatial data using machine learning[J]. Science of the Total Environment, 2019, 668: 1317-1327. DOI:10.1016/j.scitotenv.2019.03.045 |
| [10] | DeSimone L A, Pope J P, Ransom K M. Machine-learning models to map pH and redox conditions in groundwater in a layered aquifer system, Northern Atlantic Coastal Plain, eastern USA[J]. Journal of Hydrology: Regional Studies, 2020, 30. DOI:10.1016/j.ejrh.2020.100697 |
| [11] | Rahmati O, Choubin B, Fathabadi A, et al. Predicting uncertainty of machine learning models for modelling nitrate pollution of groundwater using quantile regression and UNEEC methods[J]. Science of the Total Environment, 2019, 688: 855-866. DOI:10.1016/j.scitotenv.2019.06.320 |
| [12] | Bindal S, Singh C K. Predicting groundwater arsenic contamination: Regions at risk in highest populated state of India[J]. Water Research, 2019, 159: 65-76. DOI:10.1016/j.watres.2019.04.054 |
| [13] |
杜尚海, 古成科, 张文静. 随机森林理论及其在水文地质领域的研究进展[J]. 中国环境科学, 2022, 42(9): 4285-4295. Du S H, Gu C K, Zhang W J. A review on the progresses in random forests theory and its applications in hydrogeology[J]. China Environmental Science, 2022, 42(9): 4285-4295. DOI:10.3969/j.issn.1000-6923.2022.09.036 |
| [14] | Mukherjee A, Sarkar S, Chakraborty M, et al. Occurrence, predictors and hazards of elevated groundwater arsenic across India through field observations and regional-scale AI-based modeling[J]. Science of the Total Environment, 2021, 759. DOI:10.1016/j.scitotenv.2020.143511 |
| [15] | Podgorski J, Berg M. Global analysis and prediction of fluoride in groundwater[J]. Nature Communications, 2022, 13(1). DOI:10.1038/s41467-022-31940-x |
| [16] | Liu H X, Li J X, Cao H L, et al. Prediction modeling of geogenic iodine contaminated groundwater throughout China[J]. Journal of Environmental Management, 2022, 303. DOI:10.1016/j.jenvman.2021.114249 |
| [17] |
王宗侠, 刘苏峡. 1990-2020年天山北坡地下水储量估算及其时空演变规律[J]. 地理学报, 2023, 78(7): 1744-1763. Wang Z X, Liu S X. Estimation and spatiotemporal evolution of groundwater storage on the northern slope of the Tianshan Mountains over the past three decades[J]. Acta Geographica Sinica, 2023, 78(7): 1744-1763. |
| [18] | Liu Q, Gui D W, Zhang L, et al. Simulation of regional groundwater levels in arid regions using interpretable machine learning models[J]. Science of the Total Environment, 2022, 831. DOI:10.1016/J.SCITOTENV.2022.154902 |
| [19] |
王焰新, 曹海龙, 谢先军, 等. 基于树的机器学习方法预测地质成因劣质地下水空间分布[J]. 安全与环境工程, 2022, 29(5): 58-64, 77. Wang Y X, Cao H L, Xie X J, et al. Predicting the spatial distribution of geogenic contaminated groundwater using Tree-based machine learning methods[J]. Safety and Environmental Engineering, 2022, 29(5): 58-64, 77. |
| [20] |
崔佳旭, 杨博. 贝叶斯优化方法和应用综述[J]. 软件学报, 2018, 29(10): 3068-3090. Cui J X, Yang B. Survey on Bayesian optimization methodology and applications[J]. Journal of Software, 2018, 29(10): 3068-3090. |
| [21] | Alibrahim H, Ludwig S A. Hyperparameter optimization: Comparing genetic algorithm against grid search and Bayesian optimization[A]. In: 2021 IEEE Congress on Evolutionary Computation (CEC)[C]. Kraków, Poland: IEEE, 2021. 1551-1559. |
| [22] | Sun D L, Xu J H, Wen H J, et al. Assessment of landslide susceptibility mapping based on Bayesian hyperparameter optimization: A comparison between logistic regression and random forest[J]. Engineering Geology, 2021, 281. DOI:10.1016/j.enggeo.2020.105972 |
| [23] | 刘斌, 于德胜, 门国发, 等. 塔里木盆地地下水勘查[M]. 北京: 地质出版社, 2009. |
| [24] | Ahmad M, Chand S, Rafique H M. Predicting the spatial distribution of sulfate concentration in groundwater of Jampur-Pakistan using geostatistical methods[J]. Desalination and Water Treatment, 2016, 57(58): 28195-28204. DOI:10.1080/19443994.2016.1182076 |
| [25] | Saha N, Bodrud-Doza M, Islam A R M T, et al. Hydrogeochemical evolution of shallow and deeper aquifers in central Bangladesh: arsenic mobilization process and health risk implications from the potable use of groundwater[J]. Environmental Earth Sciences, 2020, 79(20). DOI:10.1007/s12665-020-09228-4 |
| [26] | Zhang J, Zhou J L, Zhou Y Z, et al. Hydrogeochemical characteristics and groundwater quality assessment in the plain area of Yarkant River Basin in Xinjiang, P.R. China[J]. Environmental Science and Pollution Research, 2021, 28(24): 31704-31716. DOI:10.1007/s11356-021-12851-8 |
| [27] |
闫志雲, 曾妍妍, 周金龙, 等. 叶尔羌河流域平原区地下水污染风险评价[J]. 环境科学, 2023, 44(6): 3237-3246. Yan Z Y, Zeng Y Y, Zhou J L, et al. Groundwater pollution risk assessment in plain area of the Yarkant River Basin[J]. Environmental Science, 2023, 44(6): 3237-3246. |
| [28] | Yang J, Huang X. The 30 m annual land cover dataset and its dynamics in China from 1990 to 2019[J]. Earth System Science Data, 2021, 13(8): 3907-3925. DOI:10.5194/essd-13-3907-2021 |
| [29] | He S, Wu J H. Relationships of groundwater quality and associated health risks with land use/land cover patterns: a case study in a loess area, Northwest China[J]. Human and Ecological Risk Assessment: An International Journal, 2019, 25(1-2): 354-373. DOI:10.1080/10807039.2019.1570463 |
| [30] | Johnson T D, Belitz K. Assigning land use to supply wells for the statistical characterization of regional groundwater quality: correlating urban land use and VOC occurrence[J]. Journal of Hydrology, 2009, 370(1-4): 100-108. DOI:10.1016/j.jhydrol.2009.02.056 |
| [31] | Bawa R, Dwivedi P. Impact of land cover on groundwater quality in the Upper Floridan Aquifer in Florida, United States[J]. Environmental Pollution, 2019, 252: 1828-1840. DOI:10.1016/j.envpol.2019.06.054 |
| [32] | Knoll L, Breuer L, Bach M. Nation-wide estimation of groundwater redox conditions and nitrate concentrations through machine learning[J]. Environmental Research Letters, 2020, 15(6). DOI:10.1088/1748-9326/ab7d5c |
| [33] | Garrido-Merchán E C, Hernández-Lobato D. Dealing with categorical and integer-valued variables in Bayesian optimization with Gaussian processes[J]. Neurocomputing, 2020, 380: 20-35. DOI:10.1016/j.neucom.2019.11.004 |
| [34] | Breiman L. Random forest[J]. Machine Learning, 2001, 45(1): 5-32. DOI:10.1023/A:1010933404324 |
| [35] | Wu C, Fang C, Wu X, et al. Health-risk assessment of arsenic and groundwater quality classification using random forest in the yanchi region of northwest China[J]. Exposure and Health, 2020, 12(4): 761-774. DOI:10.1007/s12403-019-00335-7 |
| [36] | Nembrini S, König I R, Wright M N. The revival of the Gini importance?[J]. Bioinformatics, 2018, 34(21): 3711-3718. DOI:10.1093/bioinformatics/bty373 |
| [37] | Schober P, Boer C, Schwarte L A. Correlation coefficients: Appropriate use and interpretation[J]. Anesthesia & Analgesia, 2018, 126(5): 1763-1768. |
| [38] | Zhang J, Zhou J L, Chen Y F, et al. Identifying the factors controlling surface water and groundwater chemical characteristics and irrigation suitability in the Yarkant River Basin, northwest China[J]. Environmental Research, 2023, 223. DOI:10.1016/j.envres.2023.115452 |
| [39] |
康宁, 唐欢, 陈硕, 等. 叶尔羌河流域地下水环境背景值研究[J]. 地下水, 2016, 38(5): 80-82. Kang N, Tang H, Chen S, et al. Study on groundwater environmental background values in Yarkant River Basin[J]. Ground Water, 2016, 38(5): 80-82. DOI:10.3969/j.issn.1004-1184.2016.05.030 |
| [40] | Xiao T Y, Muhammad A M, Pan X, et al. Spatial distribution and risk identification of arsenic contamination in water and soil through GIS-based interpolation techniques in Jianghan Plain, Central China[J]. Frontiers in Environmental Science, 2022, 10. DOI:10.3389/fenvs.2022.1001862 |
| [41] |
张杰, 周金龙, 乃尉华, 等. 新疆叶尔羌河流域平原区浅层地下水咸化空间分布及成因[J]. 农业工程学报, 2019, 35(23): 126-134. Zhang J, Zhou J L, Nai W H, et al. Spatial distribution and cause of salinization of shallow groundwater in plain terrain of the Yarkant River Basin, Xinjiang[J]. Transactions of the Chinese Society of Agricultural Engineering, 2019, 35(23): 126-134. DOI:10.11975/j.issn.1002-6819.2019.23.016 |
| [42] |
张杰. 叶尔羌河流域平原区地下水水质演化及其形成机理研究[D]. 乌鲁木齐: 新疆农业大学, 2021. Zhang J. Evolution of groundwater quality and its formation mechanism in plain area of Yarkant River Basin[D]. Urumqi: Xinjiang Agricultural University, 2021. |
| [43] |
张杰, 周金龙, 曾妍妍, 等. 新疆叶尔羌河流域地表水水化学特征及控制因素[J]. 环境科学, 2021, 42(4): 1706-1713. Zhang J, Zhou J L, Zeng Y Y, et al. Hydrochemical characteristic and their controlling factors in the Yarkant River Basin of Xinjiang[J]. Environmental Science, 2021, 42(4): 1706-1713. |
| [44] | Vitòria L, Otero N, Soler A, et al. Fertilizer characterization: isotopic data (N, S, O, C, and Sr)[J]. Environmental Science & Technology, 2004, 38(12): 3254-3262. |
| [45] | Kivi S T, Bailey R T. Modeling sulfur cycling and sulfate reactive transport in an agricultural groundwater system[J]. Agricultural Water Management, 2017, 185: 78-92. DOI:10.1016/j.agwat.2017.02.002 |
| [46] | Wang H Y, Guo H M, Xiu W, et al. Indications that weathering of evaporite minerals affects groundwater salinity and as mobilization in aquifers of the northwestern Hetao Basin, China[J]. Applied Geochemistry, 2019, 109. DOI:10.1016/j.apgeochem.2019.104416 |
| [47] | Craw D, Rufaut C, Pillai D, et al. Geochemical evolution of high-pH sodic salt pans in Central Otago, New Zealand[J]. New Zealand Journal of Geology and Geophysics, 2022, 1. DOI:10.1080/00288306.2022.2076701 |
| [48] |
张杰. 浅层地下水位波动对沙地土壤氮素运移的影响[D]. 北京: 中国地质大学, 2021. Zhang J. Effects of fluctuation of shallow groundwater level on soil nitrogen transport in sandy land[D]. Beijing: China University of Geosciences, 2021. |
| [49] | Kim P G, Tarafdar A, Kwon J H. Effect of soil pH on the sorption capacity of soil organic matter for polycyclic aromatic hydrocarbons in unsaturated soils[J]. Pedosphere, 2023, 33(2): 365-371. DOI:10.1016/j.pedsph.2022.06.049 |
| [50] | Ransom K M, Nolan B T, Stackelberg P E, et al. Machine learning predictions of nitrate in groundwater used for drinking supply in the conterminous United States[J]. Science of the Total Environment, 2022, 807. DOI:10.1016/j.scitotenv.2021.151065 |
| [51] | Wang P L, Zhang D, Tao X, et al. A parsimonious model for predicting the NO3 - [J]. Journal of Hydrology, 2023, 619. DOI:10.1016/j.jhydrol.2023.129356 |
| [52] | El Bilali A, Taleb A, Brouziyne Y. Groundwater quality forecasting using machine learning algorithms for irrigation purposes[J]. Agricultural Water Management, 2021, 245. DOI:10.1016/j.agwat.2020.106625 |
| [53] | Yesilnacar M I, Sahinkaya E. Artificial neural network prediction of sulfate and SAR in an unconfined aquifer in southeastern Turkey[J]. Environmental Earth Sciences, 2012, 67(4): 1111-1119. DOI:10.1007/s12665-012-1555-9 |
| [54] | Lischeid G. Investigating short-term dynamics and long-term trends of SO4 in the runoff of a forested catchment using artificial neural networks[J]. Journal of Hydrology, 2001, 243(1-2): 31-42. DOI:10.1016/S0022-1694(00)00399-1 |
| [55] | Turner R, Eriksson D, McCourt M, et al. Bayesian optimization is superior to random search for machine learning hyperparameter tuning: Analysis of the Black-Box optimization challenge 2020[A]. In: Proceedings of the NeurIPS 2020 Competition and Demonstration Track[C]. Vancouver: PMLR, 2021. 3-26. |
| [56] | Penny J, Ordens C M, Barnett S, et al. Small-scale land use change modelling using transient groundwater levels and salinities as driving factors-An example from a sub-catchment of Australia's Murray-Darling Basin[J]. Agricultural Water Management, 2023, 278. DOI:10.1016/j.agwat.2023.108174 |
| [57] | Salem A, Abduljaleel Y, Dezső J, et al. Integrated assessment of the impact of land use changes on groundwater recharge and groundwater level in the Drava floodplain, Hungary[J]. Scientific Reports, 2023, 13. DOI:10.1038/s41598-022-21259-4 |
| [58] | Sumdang N, Chotpantarat S, Cho K H, et al. The risk assessment of arsenic contamination in the urbanized coastal aquifer of Rayong groundwater basin, Thailand using the machine learning approach[J]. Ecotoxicology and Environmental Safety, 2023, 253. DOI:10.1016/J.ECOENV.2023.114665 |
| [59] | Kumar S, Pati J. Machine learning approach for assessment of arsenic levels using physicochemical properties of water, soil, elevation, and land cover[J]. Environmental Monitoring and Assessment, 2023, 195(6). DOI:10.1007/S10661-023-11231-8 |
 2024, Vol. 45
2024, Vol. 45


