环境科学  2024, Vol. 45 Issue (5): 2516-2524   PDF    
引用本文
符传博, 林建兴, 唐家翔, 丹利. 海口市臭氧浓度统计预报模型的构建与效果评估[J]. 环境科学, 2024, 45(5): 2516-2524.
FU Chuan-bo, LIN Jian-xing, TANG Jia-xiang, DAN Li. Establishment and Effective Evaluation of Haikou Ozone Concentration Statistical Prediction Model[J]. Environmental Science, 2024, 45(5): 2516-2524.
海口市臭氧浓度统计预报模型的构建与效果评估
符传博1,2, 林建兴3, 唐家翔3, 丹利4     
1. 海南省气象科学研究所, 海口 570203;
2. 海南省南海气象防灾减灾重点实验室, 海口 570203;
3. 海南省气象台, 海口 570203;
4. 中国科学院大气物理研究所东亚区域气候-环境重点实验室, 北京 100029
收稿日期: 2023-06-05; 修订日期: 2023-08-06
基金项目: 国家自然科学基金项目（42065010, 42141017）；海南省重大科技计划项目（ZDKJ202007）；海南省自然科学基金项目（422RC802, 421QN0967）；海南省院士创新平台科研项目（YSPTZX202143）
作者简介: 符传博（1985~）, 男, 硕士, 正高级工程师, 主要研究方向为大气环境与大气污染, E-mail：hnfuchuanbo@163.com
通信作者: 林建兴, E-mail：ljx_1015_9332515@163.com
摘要: 主要利用2015 ~ 2020年海口市臭氧（O3）浓度资料和ERA5再分析资料, 基于污染物浓度控制方程挑选出海口市O3-8h浓度（日最大8 h滑动平均）的15个关键预报因子, 构建了多元线性回归模型（MLR）、支持向量机模型（SVM）和BP神经网络模型（BPNN）, 并对2021年海口市O3-8h浓度进行预测和效果检验. 结果表明, O3-8h浓度与关键预报因子的相关系数绝对值主要分布在0.2 ~ 0.507之间, 其中1 000 hPa的相对湿度（RH1000）和风向（WD1000）, 875 hPa的经向风（v875）的相关系数绝对值超过了0.4, 具有较好的指示作用. 3个预报模型基本能预报出海口市O3-8h浓度冬半年偏高, 夏半年偏低的变化趋势, 其中BPNN模型的标准误差（RMSE）数值最小（22.29 μg·m-3）. 实测值与3个统计模型预报值的相关系数从大到小排列为：0.733（BPNN） > 0.724（SVM） > 0.591（MLR）, 均通过了99.9%的信度检验. O3-8h浓度等级预报的结果检验表明, 3个预报模型的TS评分均随着O3-8h浓度等级的上升而下降, 而漏报率（PO）和空报率（NH）随着O3-8h浓度等级的上升而上升. SVM和BPNN模型在3个等级预报中TS评分均略高于MLR模型, 特别是在轻度污染等级, TS评分还维持在70%以上, 具有较好的预报性能.
关键词: 臭氧（O3）      多元线性回归      支持向量机      BP神经网络      预报评估      海口市     
Establishment and Effective Evaluation of Haikou Ozone Concentration Statistical Prediction Model
FU Chuan-bo1,2 , LIN Jian-xing3 , TANG Jia-xiang3 , DAN Li4     
1. Hainan Institute of Meteorological Science, Haikou 570203, China;
2. Key Laboratory of South China Sea Meteorological Disaster Prevention and Mitigation of Hainan Province, Haikou 570203, China;
3. Hainan Meteorological Observatory, Haikou 570203, China;
4. Key Laboratory of Regional Climate-Environment Research for Temperate East Asia, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029, China
Abstract: This study selected 15 key predictors of the maximum of 8-hour averaged ozone (O3) concentration (O3-8h), using the O3 concentration of Haikou and ERA5 reanalysis data from 2015 to 2020, and constructed a multiple linear regression (MLR) model, support vector machine (SVM) model, and BP neural network (BPNN) model, to predict and test the O3-8h concentration of Haikou in 2021. The results showed that the absolute value of correlation coefficients between the O3-8h and related key prediction factors was mainly among 0.2 and 0.507. The 1 000 hPa relative humidity (RH1000), wind direction (WD1000), and 875 hPa meridional wind (v875) showed a good indicative effect on the O3-8h, with the absolute correlation value exceeding 0.4. The three prediction models could predict the seasonal variation in the O3-8h in Haikou, which was larger in the winter half year and smaller in the summer half year. The root mean square error(RMSE) was the smallest (22.29 μg·m-3) in the BPNN model. The correlation coefficients between the predicted values of three statistical models and observations were ranked as 0.733 (BPNN) > 0.724 (SVM) > 0.591 (MLR), all passing the 99.9% significance test. For the prediction of the O3-8h level, we found that TS scores of these three prediction models decreased with the increase in O3-8h concentration level. Relatively, the point over rate and not hit rate increased with the rise in O3-8h concentration level. TS scores of the SVM and BPNN model were relatively larger than those of MLR, especially in the light pollution level with TS scores remaining above 70%, indicating a better prediction capability.
Key words: ozone (O3)      multiple linear regression      support vector machine      BP neural network      assessment of forecast results      Haikou City     

近年来, 随着《大气污染防治行动计划》等一系列大气治理工作的开展和落实, 以及产业结构调整的持续推进, 我国PM2.5和PM10等一次污染物已经得到有效控制, 但臭氧（O3）等二次污染物的治理并未得到有效改善[1, 2]. 根据生态环境部门的监测数据显示[3], 2021年京津冀及周边地区、长三角地区和汾渭平原以O3为首要污染物的超标天数占总超标天数分别为41.8%、55.4%和39.3%, 而全国339个地级及以上城市, 以O3为首要污染物的超标天数占总超标天数的比例只为34.7%, 表明O3已经成为影响我国重要区域大气环境的首要污染物, 其形成机制更为复杂, 污染防控难度更大[4, 5]. O3作为一种极其不稳定的有毒气体, 其浓度上升会严重影响公众健康和社会形象[6, 7], 准确预报城市O3污染状况有助于建立有效的大气污染预警机制和采取灵活的控制政策减轻大气污染[8].

目前空气污染预报方法主要分为潜势预报、统计预报和数值预报这3种[9]. 潜势预报是对影响空气中污染物的聚集、扩散等气象条件和背景场进行预报, 属于定性预报. 这一方法比较单一, 仅分析气象条件或气象因子等要素, 缺乏污染源和其他相关因素的结合分析, 预报结果可能存在较大偏差[10, 11]. 近年来, 大量学者对潜势预报的研究升级为各种大气污染物指数的研究, 如静稳指数[12]、PLAM指数[13]、大气自净能力系数[14]和大气扩散能力指数[15]等, 对大气的静稳情况有一定的指示意义. 统计预报和数值预报是可以直接给出大气污染物浓度预报结果, 属于定量预报. 数值预报以大气动力学理论为基础, 通过数值求解物质守恒数学模型或其在各种近似条件下的简化形式, 进而得到各种污染过程演变特征, 解析污染物的来源和去向, 模拟预测应急控制效果等[16]. 目前大气环境数值模型先后发展出了三代, 第一代为拉格朗日轨迹模型[17], 在局地范围内少数污染物的预报应用较为广泛；第二代为欧拉网格模型[18], 包括城市大气质量模型（uban airshed model, UAM）、区域酸沉降模型（regional acid deposition model, RADM1和RADM2）和区域氧化物模型（regional oxidant model, ROM）；第三代为区域多尺度空气质量模型（Model-3/CMAQ）[19], 由美国环保局1998年提出, 随后做了进一步完善. 数值预报具有较为完善的理论基础, 能够定量给出区域内不同大气污染物的传输、扩散、转化以及沉降过程, 但同时要求也较高, 如气象背景场需要相对准确, 排放源清单尽可能完备, 污染物扩散过程的物理化学模型相对合理等, 这一定程度上对数值预报方法的广泛应用形成了限制[20]. 统计预报是指利用长期气象与污染物浓度变化资料, 针对特定区域或城市建立影响因子与污染物浓度之间定量或半定量的关系. 与数值预报不同, 统计预报不涉及太多的大气化学和大气动力学理论, 只需分析影响要素与污染物发展规律就可完成预报[21]. 早期的统计预报主要分为3类：回归模型、分类法和趋势外推法[22], 其中回归模型在空气质量预报领域应用较为广泛, 如沈劲等[23]利用气象因子聚类与多元线性回归方法（multiple linear regression, MLR）, 开发了可以较好模拟顺德区多种环境要素的预报模型. 李颖若等[24]采用MLR方法, 定量评估了气象条件和空气污染控制措施对APEC期间北京空气质量的影响, 结果表明基于气象因子建立的MLR模型效果较好. 近十几年, 随着大数据时代的来临, 基于统计学和人工智能发展而来的机器学习快速崛起并得到广泛应用[25], 常见的机器学习方法包括支持向量机（multiple linear regression, SVM）、BP神经网络（BP neural network, BPNN）和贝叶斯网络等[26]. 苏筱倩等[27]利用SVM方法预报了南京2016年5月高污染期间O3浓度, 发现该方法比MLR方法具有明显优势. 朱媛媛等[28]评估了BPNN方法在京津冀地区O3浓度预报效果, 发现BPNN方法在O3超标情况多发的月份预报效果较好.

海口市位于海南岛北部, 气候暖热湿润, 环境优美[29]. 近年来随着社会经济的快速增长, O3污染事件也时有发生[30, 31], O3已经成为制约海口市空气质量持续改善的主要大气污染物. 一方面, 海口市地处热带, 常年气温较高, 日照时间长, 太阳辐射强, 气象条件较有利于光化学反应的发生；另一方面海口市毗邻珠三角地区, 冬季风携带而来的北方O3及其前体物进一步增加了海口市O3污染的复杂性[32]. 目前对于海口市O3浓度预报的方法研究, 主要集中于数值预报模式[33], 而基于统计模型的O3浓度预报的研究较少. 为了更好地实现海口市乃至全省气象部门和生态环境部门O3浓度预报工作的开展和预报质量的提高, 本文利用2015 ~ 2020年海口市最大8 h滑动平均的O3逐日数据（O3-8h）和同期的EAR5再分析资料, 基于污染物浓度控制方程, 在考虑垂直边界层内各气象要素后对预报因子进行筛选, 并利用MLR[34, 35]、SVM[27]和BPNN算法[28, 32, 36]构建海口市O3浓度预报模型, 利用观测数据对2021年的预报结果进行了检验, 以期为海口市行之有效的O3污染防治提供依据和参考.

1 材料与方法 1.1 数据资料

本文主要采用了海口市2015 ~ 2021年环境监测中心站监测的包括海南大学站、海南师范大学站、龙华区环保局宿舍站和秀英区海南医院站, 共4个国控站, 数据分辨率为1 h, 数据有效率均在99.9%以上, 站点位置信息可参考文献[37]. O3浓度超标值参考标准为《环境空气质量指数（AQI）技术规定》（HJ 633-2012）和《环境空气质量标准》（GB 3095-2012）, ρ（O3-8h）等级标准：0 ~ 100 μg·m-3为优；101 ~ 160 μg·m-3为良；161 ~ 215 μg·m-3为轻度污染；216 ~ 265 μg·m-3为中度污染；266 ~ 800 μg·m-3为重度污染. 其中大于160 μg·m-3时, 为O3超标日. 为了将垂直边界层内各气象要素作为预报因子纳入统计模型中, 再分析资料使用了ECMWF发布的第5代资料（ERA5）[38], 数据源自哥白尼气候变化服务中心数据库（https://cds.climate.copernicus.eu）, 时间分辨率为1 h, 空间分辨率为0.25°× 0.25°, 要素包括1 000 ~ 850 hPa的气温、相对湿度和水平风向风速等, 以及近地面的边界层高度、地面气压、总降水量、总云量和地表太阳辐射.

1.2 研究方法

本文的基本思路是利用2015 ~ 2020年挑选出来的海口市气象因子和O3-8h浓度资料进行MLR建模, 同时进行SVM和BPNN方法训练, 最后利用2021年的O3-8h浓度观测值对3个统计模型的预报结果进行检验. 具体步骤如下.

（1）根据污染物浓度控制方程, 首先挑选出海口市不同层次的气象因子作为预选因子, 包括与O3-8h浓度相关的1 000 ~ 850 hPa高空因子和地面因子.

（2）分别计算出海口市2015 ~ 2020年逐日的O3-8h浓度与各个预选因子的相关系数, 根据相关系数绝对值大小进行排序, 且基于预报因子的多元性原则, 挑选数值较大的气象因子作为预报因子, 同时尽量避免同种因子相邻气压层或同一高度相似气象因子被挑选.

（3）基于2015 ~ 2020年挑选出来的数据, 构建MLR方程并对2021年海口市O3-8h浓度进行预报. SVM和BPNN的做法是随机抽取2015 ~ 2020年中70%的数据作为训练数据集, 剩余的30%用作验证数据集并对各个参数权重进行调试. 其中SVM模型核函数为RBF, 核函数系数为4.1, 错误项的惩罚因子为100, 训练的标准误差（root mean square error, RMSE）为14.72 μg·m-3, 测试的RMSE为19.29 μg·m-3. BPNN本文采用了3层隐含层, 为了抑制过拟合, 加入Dropout函数, 丢弃率设置为0.05, 采用前馈神经网络运算, 其中激励函数采用Relu, 学习率为0.01. 最后基于稳定的SVM和BPNN模型, 将2021年的预报因子代入模型并进行预报. 此外, 为避免各因子间数量级差异造成的预报误差, 所有的气象因子都进行了归一化处理.

在对3个统计模型2021年海口市O3-8h浓度预报结果进行评估时, 本文主要选择标准误差（RMSE）、平均偏差（mean bias, MB）、归一化偏差（mean normalized bias, MNB）和相关系数（R）来进行. RMSE能反映出预报值和观测值的差值, MB的大小主要表示样本总体预报值比观测值偏大或偏小的数值, MNB反映的是预报值比观测值偏大或偏小的程度, 而相关系数R表示了预报值与观测值相关关系的密切程度[33]. 此外对O3-8h浓度等级评估时, 本文主要采用的是TS评分、漏报率（point over, PO）、空报率（not hit, NH）和预报偏差（bias, B）来进行检验, 具体公式为：

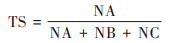
(1)
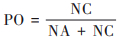
(2)
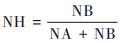
(3)
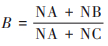
(4)

式中, NA、NB和NC的物理意义见表 1. TS（%）评分数值越大表示O3-8h浓度等级的预报准确性越高, 其区间在0 ~ 1之间. PO（%）和NH（%）表示的是漏报次数和空报次数与观测次数的比值, 其区间也分布在0 ~ 1之间, 数值越小反映该模型对O3-8h浓度等级的预报的准确率越高. B（%）的数值区间在0 ~ ±∞之间, B大于1时表示O3-8h浓度等级在预报中出现的次数偏多于实际出现的次数；反之, B小于1时则表示模型对O3-8h浓度等级少报.

表 1 O3-8h浓度等级预报检验分类 Table 1 Classification of O3-8h level forecast verification

2 结果与讨论 2.1 O3-8h浓度与关键气象因子的确立

为了给出海口市不同层次气象因子对O3-8h浓度的影响, 进而确定关键性气象因子, 并用于预报方程的构建和预报效果检验. 本文首先采用污染物浓度控制方程[39]：

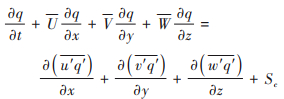
(5)

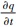
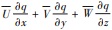
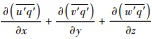
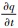
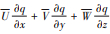
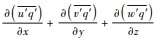
式中, 为污染物浓度的局地变化, 为污染物的平流输送, 为污染物的湍流输送, Sc为污染物的体源项. 从中可知, 污染物浓度的局地变化主要受污染物的平流输送、湍流输送以及体源项Sc影响. 体源项Sc包括排放源, 干湿沉降和化学反应. 考虑到污染物主要集中在边界层内, 其浓度主要受边界层内气象因子的共同作用影响, 因此O3-8h浓度预选因子如下.

（1）平流输送项, 主要与风速大小和污染物浓度梯度有关, 由于难于获得瞬时O3浓度梯度, 因此本文只选取了1 000 ~ 850 hPa高度上各个风速（WS）和风向（WD）作为预选因子之一.

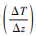
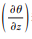
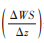
（2）湍流输送项, 包括热力湍流和动力湍流两种, 可分别用逆温强度及热力稳定度和风切变表示, 本文选取了相邻两气压层间风速差、位温差和温度差作为预选因子之一.

（3）对流层O3是一种光化学反应产物, 属于二次污染物, 因此本文中不考虑O3的排放源.

（4）植被气孔沉降过程是大气中O3干沉降最重要的过程之一[40], 而本文主要基于气象要素进行模型构建, 因此不考虑干沉降的影响, 只考虑不同水汽条件下的光化学分解效应等, 故引入相对湿度（RH）及相对湿度差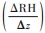作为预选因子.

（5）边界层高度（PBLH）决定了污染物扩散的大气环境容量和有效空气体积. 通常边界层较低时, 由于垂直扩散条件受到抑制, 致使边界层内污染物浓度升高. 海口市PBLH数据从ERA5中直接获得.

（6）地表通风系数（SVC）, 其可表示边界层内污染物的水平扩散和输送的能力, 一般值越小越不利于污染物扩散. 其大小可用大气边界层高度乘以边界层高度内平均风速表示[41]. 计算公式见式（6）：

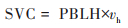
(6)

式中, SVC为地表通风系数, vh为1 000 hPa平均风速. 此外, 本文地面气象要素还考虑了地面气压（SP）、总降水量（TP）、总云量（TCC）和地表太阳辐射（SSRD）, 数据直接从ERA5中获得.

本文中位温（θ）由温度（T）经公式（7）计算得到：

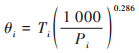
(7)

式中, i表示为气压高度, Pi为对应高度的大气压强.

风向（WD）由u和v经公式（8）得到：

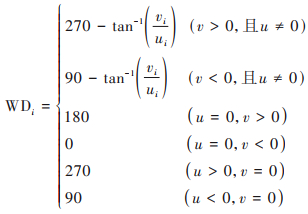
(8)

式中, i表示气压高度, ui和vi分别为对应高度的水平u风速和水平v风速, WD表示风的来向.

表 2给出了O3-8h浓度预报因子的所有预选因子. 包括1 000 ~ 850 hPa共7个层次的温度（T）、位温（θ）、相对湿度（RH）、垂直速度（W）、水平速度（u）、水平速度（v）、风速（WS）和风向（WD）, 还有相邻气压间的温度差（ΔT）、位温差（Δθ）、相对湿度差（ΔRH）和风速差（ΔWS）, 最后是地面的边界层高度（PBLH）、地表通风系数（SVC）、地面气压（SP）、总降水量（TP）、总云量（TCC）和地表太阳辐射（SSRD）, 共86个预选因子.

表 2 O3-8h浓度预选预报因子 Table 2 Preselected prediction factors of O3-8h

计算2015 ~ 2020年逐日的O3-8h浓度与86个预选因子的相关系数, 综合考虑相关系数绝对值大小和基于预报因子的多元性原则, 避免同种因子相邻气压层或同一高度相似气象因子被挑选, 最后共选出15个预报因子见表 3所示. 从中可以清楚发现, 海口市O3-8h浓度与T850、θ850、RH1000、W1000、u875、v875、WD1000、ΔRH975-950和TCC呈负相关关系, 与ΔT975-950、Δθ975-950、ΔWS1000-975、PBLH、SVC和SP呈正相关关系, 其中边界层下层的相对湿度RH1000和风向WD1000, 上层的经向风v875与O3-8h浓度的相关系数绝对值超过了0.4, 具有较好的指示作用. RH1000与光化学反应有关, RH偏高时, 大气中水汽含量偏大, 一方面会减弱太阳紫外辐射；另一方面会与O3发生化学反应, 进而降低对流层O3浓度[34]. WD1000和v875因子与外源输送有关, 说明合适的风向有利于北方气流携带O3及其前体物输送至海口市, 影响O3浓度的变化. 边界层上层的温度和位温（T850和θ850）、下层的温度差和位温差（ΔT975-950和Δθ975-950）和地面气压（SP）与O3-8h浓度的相关系数绝对值在0.3 ~ 0.4之间, 也有较好的指示作用. 这些因子主要与天气形势的变化相关, 海口市O3-8h浓度超标多与冷空气南下有关[32], 冷高压控制会引起地面气压升高, 气温下降, 配合上下层逆温层的出现, 有利于地面污染物浓度上升. 此外, 海口市O3-8h浓度还与边界层下层风速（W1000）、上层纬向风（u875）、下层的相对湿度差（ΔRH975-950）和风速差（ΔWS1000-975）, 以及边界层高度（PBLH）、地表通风系数（SVC）和总云量（TCC）有关, 相关系数绝对值均在0.3以下, 有一定的指示作用. 这些因子涉及影响O3浓度的水汽、天空状况、水平输送和垂直扩散条件等, 体现了海口市O3污染的复杂性.

表 3 O3-8h浓度与入选的预报因子相关系数1） Table 3 Correlation coefficient between O3-8h and selected forecast factors

2.2 O3-8h浓度预报效果检验

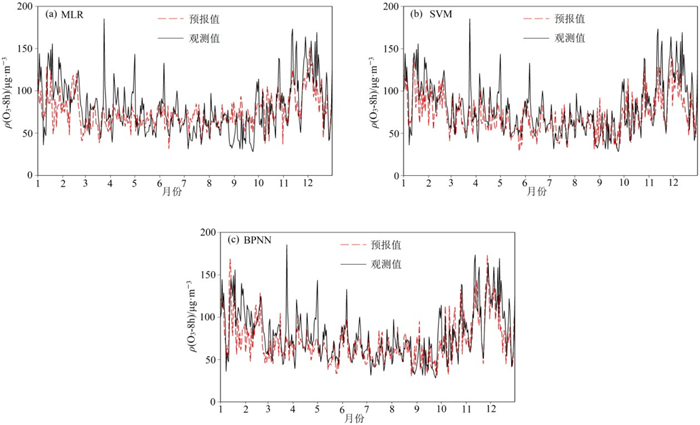
本小节利用前面挑选出来的15个气象因子, 首先构建海口市O3-8h浓度的MLR预报模型, 并利用2021年的气象因子进行预报；其次利用2015 ~ 2020年中15个气象因子和O3-8h浓度资料随机选择70%数据作为训练数据集, 剩余30%的数据作验证数据集并对SVM和BPNN模型的各个参数权重进行调试, 待模型稳定后将2021年的预报因子代入两个模型并进行预报. 最后得出MLR、SVM和BPNN模型的2021年O3-8h浓度预报结果并与观测值进行对比分析, 结果如图 1所示. 从中可知, 3个模型基本能预报出海口市O3-8h浓度的变化趋势, 即2021年O3-8h浓度呈现冬半年偏高, 夏半年偏低的变化特征, 与观测值的基本一致. 对比而言, MLR模型预报值总体偏低于观测值, 且变化幅度偏小. 特别是春季的3月和4月, 秋季的10月和11月, 冬季的12月和1月, O3-8h浓度观测值偏高时段预报值明显偏低, 而在夏季的7月和8月, 预报值又略偏高于观测值. 与MLR模型不同, SVM和BPNN模型的预报值变化基本一致, 同时与实测值较为接近. 除了春季的3月和4月, 冬季的12月和1月两个模型的预报值略偏低, 部分O3-8h浓度峰值没有预报出来外, 其余时段基本预报出了O3-8h浓度观测值的变化趋势. 进一步计算O3-8h浓度观测值与3个统计模型预报值的相关系数（表 4）分别为0.591（MLR）、0.724（SVM）和0.733（BPNN）, 均通过了99.9%的信度检验, 其中SVM和BPNN模型相关系数明显偏高于MLR模型, 表明机器学习方法预报结果优于传统的回归模型.

图 1 2021年海口市O3-8h浓度3个统计模型预报值和观测值对比 Fig. 1 Comparisons between three predicted statistical models and observation for O3-8h in Haikou in 2021

表 4 3个模型O3-8h浓度预报结果检验1） Table 4 Verification of O3-8h prediction results of three models

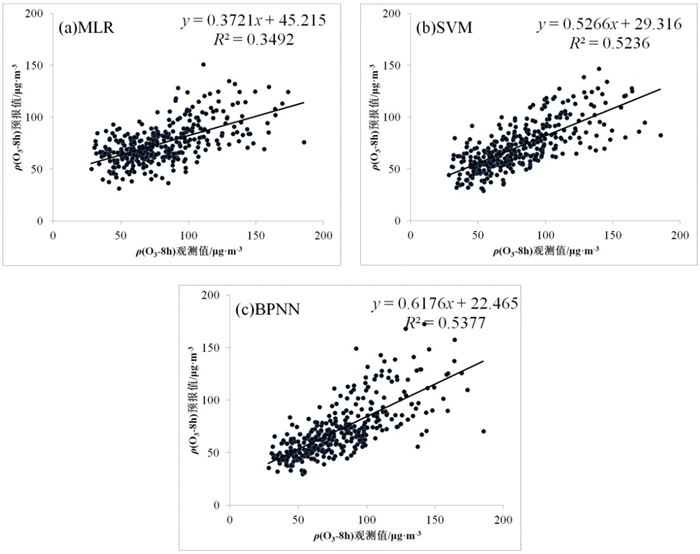
图 2进一步给出了2021年3个模型的O3-8h浓度预报值和观测值的相关性分布. 从中可知, MLR模型预报值基本偏低于观测值, 这与前面的分析一致；SVM和BPNN模型离散点分布较为一致, 在O3-8h浓度小于100 μg·m-3时段基本分布在趋势线附近, 而在O3-8h浓度大于100 μg·m-3时段分布相对较为分散, 表明两个模型对于O3-8h浓度偏大的预报均存在明显误差. 表 4给出了3个模型预报值与观测值的标准误差（RMSE）、平均偏差（MB）和归一化偏差（MNB）. 从3个模型的RMSE值来看, BPNN模型最小, 只为22.29 μg·m-3, SVM次之, 为22.48 μg·m-3, MLR最大, 为24.88 μg·m-3, 表明BPNN模型预报值与观测值最为接近, SVM模型偏差最大. 从MB值上看, 3个模型的MB值均为负值, 分布在-4.73 ~ -8.34 μg·m-3之间, 3个统计模型预报值均偏低于观测值. 其中SVM模型偏低最明显, MB值为-8.34 μg·m-3, 这可能与2021年春季和冬季的预报值偏低有关. 从MNB值上看, SVM和BPNN模型为负值, 而MLR模型MNB值为正值, 与MB值不同. 结合图 1和图 2可判断, MLR模型预报值总体比观测值小, 因而MB值为负值, 但由于个别时段预报值偏大, 致使MNB值为正值.

图 2 2021年海口市O3-8h浓度3个统计模型预报值和观测值的相关性分布 Fig. 2 Correlations between three predicted statistical models and observation for O3-8h in Haikou in 2021

2.3 O3-8h浓度等级预报效果检验

为了进一步检验2021年3个统计模型O3-8h浓度等级预报值与观测值的结果, 本小节首先统计了海口市O3-8h浓度不同等级天数和占比如表 5所示. 从中可见, 2021年海口市总体空气质量较好, O3-8h浓度等级只有3个等级, 分别是优、良和轻度污染, 没有中度污染及其以上等级出现. 大部分天数以优和良为主, 分别为284 d和76 d, 占了全年天数的77.81%和20.82%. 2021年海口市共有5 d O3-8h浓度达到轻度污染等级, 占比为1.37%. 近年来随着海口市人口规模的扩大和经济建设的加强, O3污染问题也呈现愈发严重的趋势[33, 37].

表 5 2021年海口市O3-8h等级天数和占比 Table 5 Statistical summary for O3-8h levels and proportion over Haikou City in 2021

TS评分在气象部门中广泛应用于对定量降水预报准确率的评分标准, 本小节也采用TS评分对3个统计模型的O3-8h浓度等级预报结果进行评分, 方法包括TS评分、漏报率（PO）、空报率（NH）和预报偏差（B）等, 具体公式见1.2节. 表 6给出了2021年3个模型O3-8h浓度等级预报效果. 从中可知, 海口市O3-8h浓度等级为优时, MLR、SVM和BPNN预报模型TS评分均在80%以上, 其中SVM模型的TS评分最高, 为83.94%, BPNN次之, 为82.62%, MLR最小, 只为81.85%, 同时SVM模型的PO值偏小于其余两个模型, 为2.46%. 而BPNN模型的NH值最小, 只为13.97%. 3个模型的B值均略偏高于100%, 表明对于优等级, 3个模型都略多报, 其中MLR的B值最大. 对于良等级, SVM的TS评为74.70%, 明显偏高于其余两个模型, 而PO值和NH值均最小, 分别为13.89%和15.07%, 表明SVM模型在良等级漏报和空报均最少. 3个模型的B值均略偏高于100%, 与优等级一致. 对于轻度污染等级, 3个模型TS评分均有所下降, 其中MLR模型下降至70%以下, SVM和BPNN模型在70%以上, 其中SVM模型为73.81%, 而PO值和NH值均为15.07%, 偏低于MLR和BPNN, 3个预报模型B值均为100%. 总体而言, 3个预报模型TS评分均随着O3-8h浓度等级的上升而下降, 而PO值和NH值随着O3-8h浓度等级的上升而上升, 特别是轻度污染等级, 主要是由于海口市属于空气质量较好地区, O3-8h浓度超标属于低概率事件, 2021年也只有5 d达到轻度污染等级, 因此预报难度大, 命中率较低, 导致TS评分偏低, PO和NH较高. 对比而言, SVM和BPNN模型预报效果优于MLR模型, 特别是轻度污染等级, SVM和BPNN模型的TS评分还能维持在70%以上, 表明2个模型在该等级还有一定的预报能力.

表 6 2021年3个模型O3-8h浓度等级预报结果/% Table 6 Verification of level prediction of O3-8h in three models in 2021/%

需要指出的是, 文中3个模型预报效果的检验输入的是ERA5再分析资料的气象要素结果, 后续业务应用时需使用模式气象要素的预报, 可能会对预报结果产生影响.

3 结论

（1）基于污染物浓度控制方程, 综合考虑相关系数绝对值大小和预报因子的多元性原则后, 筛选出2015 ~ 2020年逐日的海口市O3-8h浓度的15个预报因子, O3-8h浓度与T850、θ850、RH1000、W1000、u875、v875、WD1000、ΔRH975-950和TCC呈负相关关系, 与ΔT975-950、Δθ975-950、ΔWS1000-975、PBLH、SVC和SP呈正相关关系, 相关系数绝对值主要分布在0.2 ~ 0.507之间, 其中边界层下层的相对湿度RH1000和风向WD1000、上层的经向风v875与O3-8h浓度的相关系数绝对值超过了0.4, 具有较好的指示作用.

（2）利用归一化后的15个预报因子, 构建了MLR、SVM和BPNN统计模型并对2021年海口市O3-8h浓度的预报结果进行检验, 发现3个模型基本能预报出海口市O3-8h浓度冬半年偏高, 夏半年偏低的变化趋势. 其中BPNN模型的RMSE数值最小, 只为22.29 μg·m-3. 实测值与3个统计模型预报值的相关系数从大到小排列为：0.733（BPNN） > 0.724（SVM） > 0.591（MLR）, 均通过了99.9%的信度检验.

（3）对2021年3个统计模型O3-8h浓度等级预报的结果检验表明, 3个预报模型的TS评分均随着O3-8h浓度等级的上升而下降, 而PO值和NH值随着O3-8h浓度等级的上升而上升. SVM和BPNN模型在3个O3-8h浓度等级的预报中, TS评分均略高于MLR模型, 特别是轻度污染等级, TS评分还能维持在70%以上, 而MLR模型TS评分小于70%, 体现了SVM和BPNN模型均具有较好的预报性能.

参考文献
[1] Wang T, Xue L K, Brimblecombe P, et al. Ozone pollution in China: a review of concentrations, meteorological influences, chemical precursors, and effects[J]. Science of the Total Environment, 2017, 575: 1582-1596. DOI:10.1016/j.scitotenv.2016.10.081
[2] 符传博, 周航. 中国城市臭氧的形成机理及污染影响因素研究进展[J]. 中国环境监测, 2021, 37(2): 33-43.
Fu C B, Zhou H. Research progress on the formation mechanism and impact factors of urban ozone pollution in China[J]. Environmental Monitoring in China, 2021, 37(2): 33-43.
[3] 中华人民共和国生态环境保护部. 2021年中国生态环境状况公报[EB/OL]. https://www.mee.gov.cn/hjzl/sthjzk/zghjzkgb/202205/P020220527581962738409.pdf, 2022-09-24.
[4] Yu R L, Lin Y L, Zou J H, et al. Review on atmospheric ozone pollution in China: formation, spatiotemporal distribution, precursors and affecting factors[J]. Atmosphere, 2021, 12(12). DOI:10.3390/atmos12121675
[5] Li Y S, Yin S S, Yu S J, et al. Characteristics of ozone pollution and the sensitivity to precursors during early summer in central plain, China[J]. Journal of Environmental Sciences, 2021, 99: 354-368. DOI:10.1016/j.jes.2020.06.021
[6] Chen K, Zhou L, Chen X D, et al. Acute effect of ozone exposure on daily mortality in seven cities of Jiangsu Province, China: no clear evidence for threshold[J]. Environmental Research, 2017, 155: 235-241. DOI:10.1016/j.envres.2017.02.009
[7] Wang P, Shen J Y, Xia M, et al. Unexpected enhancement of ozone exposure and health risks during national day in China[J]. Atmospheric Chemistry and Physics, 2021, 21(13): 10347-10356. DOI:10.5194/acp-21-10347-2021
[8] 陈辰, 洪莹莹, 谭浩波, 等. 佛山臭氧浓度预报方程的建立与应用[J]. 环境科学, 2022, 43(10): 4316-4326.
Chen C, Hong Y Y, Tan H B, et al. Establishment and application of Foshan ozone concentration forecast equation[J]. Environmental Science, 2022, 43(10): 4316-4326.
[9] 任万辉, 苏枞枞, 赵宏德. 城市环境空气污染预报研究进展[J]. 环境保护科学, 2010, 36(3): 9-11.
Ren W H, Su C C, Zhao H D. Research progress of air pollution forecasting in urban area[J]. Environmental Protection Science, 2010, 36(3): 9-11. DOI:10.3969/j.issn.1004-6216.2010.03.004
[10] 黄晓娴, 王体健, 江飞. 空气污染潜势—统计结合预报模型的建立及应用[J]. 中国环境科学, 2012, 32(8): 1400-1408.
Huang X X, Wang T J, Jiang F. An air pollution potential forecast model combined with statistical method and its application[J]. China Environmental Science, 2012, 32(8): 1400-1408. DOI:10.3969/j.issn.1000-6923.2012.08.009
[11] 张莹, 王式功, 贾旭伟, 等. 华北地区冬半年空气污染天气客观分型研究[J]. 环境科学学报, 2018, 38(10): 3826-3833.
Zhang Y, Wang S G, Jia X W, et al. Study on an objective synoptic typing method for air pollution weather in North China during winter half year[J]. Acta Scientiae Circumstantiae, 2018, 38(10): 3826-3833.
[12] 张敏, 蔡子颖, 韩素芹. 天津静稳指数建立及在环境气象预报和评估中的应用[J]. 环境科学学报, 2020, 40(12): 4453-4460.
Zhang M, Cai Z Y, Han S Q. Establishment of stable weather index of Tianjin and its application in environmental weather forecast and assessment[J]. Acta Scientiae Circumstantiae, 2020, 40(12): 4453-4460.
[13] 王继志, 杨元琴, 王亚强, 等. PLAM指数跟踪方法对中国沙尘天气过程及其波动变化特征的研究[J]. 气象与环境学报, 2013, 29(5): 92-97.
Wang J Z, Yang Y Q, Wang Y Q, et al. Sand dust weather and its variation in China based on PLAM index tracking method[J]. Journal of Meteorology and Environment, 2013, 29(5): 92-97. DOI:10.3969/j.issn.1673-503X.2013.05.015
[14] 朱蓉, 张存杰, 梅梅. 大气自净能力指数的气候特征与应用研究[J]. 中国环境科学, 2018, 38(10): 3601-3610.
Zhu R, Zhang C J, Mei M. The climate characteristics of atmospheric self-cleaning ability index and its application in China[J]. China Environmental Science, 2018, 38(10): 3601-3610. DOI:10.3969/j.issn.1000-6923.2018.10.001
[15] 毛敏娟, 杜荣光, 齐冰. 浙江省大气扩散能力的时空分布特征[J]. 热带气象学报, 2019, 35(5): 644-651.
Mao M J, Du R G, Qi B. The spatiotemporal distribution of atmospheric diffusion capacity in Zhejiang Province[J]. Journal of Tropical Meteorology, 2019, 35(5): 644-651.
[16] 王自发, 庞成明, 朱江, 等. 大气环境数值模拟研究新进展[J]. 大气科学, 2008, 32(4): 987-995.
Wang Z F, Pang C M, Zhu J, et al. IAP Progress in atmospheric environment modeling research[J]. Chinese Journal of Atmospheric Sciences, 2008, 32(4): 987-995. DOI:10.3878/j.issn.1006-9895.2008.04.23
[17] 裴成磊, 牟江山, 张英南, 等. 广州市臭氧污染溯源: 基于拉格朗日光化学轨迹模型的案例分析[J]. 环境科学, 2021, 42(4): 1615-1625.
Pei C L, Mu J S, Zhang Y N, et al. Source apportionment of ozone pollution in Guangzhou: Case study with the application of Lagrangian photochemical trajectory model[J]. Environmental Science, 2021, 42(4): 1615-1625. DOI:10.3969/j.issn.1000-6923.2021.04.014
[18] Genc D D, Yesilyurt C, Tuncel G. Air pollution forecasting in Ankara, Turkey using air pollution index and its relation to assimilative capacity of the atmosphere[J]. Environmental Monitoring and Assessment, 2010, 166(1-4): 11-27. DOI:10.1007/s10661-009-0981-y
[19] Arnold J R, Dennis R L, Tonnesen G S. Diagnostic evaluation of numerical air quality models with specialized ambient observations: testing the community multiscale air quality modeling system (CMAQ) at selected SOS 95 ground sites[J]. Atmospheric Environment, 2003, 37(9-10): 1185-1198. DOI:10.1016/S1352-2310(02)01008-7
[20] 高雅, 刘杨, 吕佳佩. 空气质量模型研究进展综述[J]. 环境污染与防治, 2022, 44(7): 939-943.
Gao Y, Liu Y, Lyu J P. A review of air quality models research progress[J]. Environmental Pollution & Control, 2022, 44(7): 939-943.
[21] 李颖若, 韩婷婷, 汪君霞, 等. ARIMA时间序列分析模型在臭氧浓度中长期预报中的应用[J]. 环境科学, 2021, 42(7): 3118-3126.
Li Y R, Han T T, Wang J X, et al. Application of ARIMA model for mid-and long-term forecasting of ozone concentration[J]. Environmental Science, 2021, 42(7): 3118-3126.
[22] 姜有山, 陈飞, 班欣, 等. 连云港市城市空气质量预报方法研究[J]. 气象科学, 2007, 27(2): 220-225.
Jiang Y S, Chen F, Ban X, et al. The research of analysis and predication of air quality in Lianyungang City[J]. Scientia Meteorologica Sinica, 2007, 27(2): 220-225. DOI:10.3969/j.issn.1009-0827.2007.02.015
[23] 沈劲, 钟流举, 何芳芳, 等. 基于聚类与多元回归的空气质量预报模型开发[J]. 环境科学与技术, 2015, 38(2): 63-66.
Shen J, Zhong L J, He F F, et al. Development of air quality forecast model based on clustering and multiple regression[J]. Environmental Science & Technology, 2015, 38(2): 63-66.
[24] 李颖若, 汪君霞, 韩婷婷, 等. 利用多元线性回归方法评估气象条件和控制措施对APEC期间北京空气质量的影响[J]. 环境科学, 2019, 40(3): 1024-1034.
Li Y R, Wang J X, Han T T, et al. Using multiple linear regression method to evaluate the impact of meteorological conditions and control measures on air quality in Beijing during APEC 2014[J]. Environmental Science, 2019, 40(3): 1024-1034.
[25] 魏煜, 徐起翔, 赵金帅, 等. 基于机器学习算法的新冠疫情管控对河南省空气质量影响的模拟分析[J]. 环境科学, 2021, 42(9): 4126-4139.
Wei Y, Xu Q X, Zhao J S, et al. Simulation analysis of the impact of COVID-19 pandemic control on air quality in Henan Province based on machine learning algorithm[J]. Environmental Science, 2021, 42(9): 4126-4139.
[26] 芦华, 谢旻, 吴钲, 等. 基于机器学习的成渝地区空气质量数值预报PM2.5订正方法研究[J]. 环境科学学报, 2020, 40(12): 4419-4431.
Lu H, Xie M, Wu Z, et al. Adjusting PM2.5 prediction of the numerical air quality forecast model based on machine learning methods in Chengyu region[J]. Acta Scientiae Circumstantiae, 2020, 40(12): 4419-4431.
[27] 苏筱倩, 安俊琳, 张玉欣, 等. 支持向量机回归在臭氧预报中的应用[J]. 环境科学, 2019, 40(4): 1697-1704.
Su X Q, An J L, Zhang Y X, et al. Application of support vector machine regression in ozone forecasting[J]. Environmental Science, 2019, 40(4): 1697-1704.
[28] 朱媛媛, 刘冰, 桂海林, 等. 京津冀臭氧污染特征、气象影响及基于神经网络的预报效果评估[J]. 环境科学, 2022, 43(8): 3966-3976.
Zhu Y Y, Liu B, Gui H L, et al. Characteristics of ozone pollution, meteorological impact, and evaluation of forecasting results based on a neural network model in Beijing-Tianjin-Hebei region[J]. Environmental Science, 2022, 43(8): 3966-3976.
[29] 王春乙. 海南气候[M]. 北京: 气象出版社, 2014.
[30] 赵蕾, 吴坤悌, 陈明. 2013—2016年海口市空气质量特征及典型个例污染物来源分析[J]. 气象与环境学报, 2019, 35(5): 63-69.
Zhao L, Wu K T, Chen M. Characteristics of air quality in Haikou from 2013 to 2016 and pollutant source analysis during typical pollution events[J]. Journal of Meteorology and Environment, 2019, 35(5): 63-69.
[31] 符传博, 丹利, 唐家翔, 等. 2017年10月海南省一次臭氧污染特征及输送路径与潜在源区分析[J]. 环境科学研究, 2021, 34(4): 863-871.
Fu C B, Dan L, Tang J X, et al. Potential source contributions and transported routes in Hainan Province during ozone polluted episode in October 2017[J]. Research of Environmental Sciences, 2021, 34(4): 863-871.
[32] 符传博, 丹利, 唐家翔, 等. 海南省城市臭氧污染特征及气象学成因[M]. 北京: 气象出版社, 2021.
[33] 符传博, 唐家翔, 丹利, 等. 2014-2016年海口市空气质量概况及预报效果检验[J]. 环境科学学报, 2019, 39(1): 270-278.
Fu C B, Tang J X, Dan L, et al. Verification of air quality forecasted by CUACE model in Haikou City during 2014 to 2016[J]. Acta Scientiae Circumstantiae, 2019, 39(1): 270-278.
[34] 符传博, 徐文帅, 丹利, 等. 2015 ~ 2020年海南省臭氧时空变化及其成因分析[J]. 环境科学, 2022, 43(2): 675-685.
Fu C B, Xu W S, Dan L, et al. Temporal and spatial variations in ozone and its causes over Hainan Province from 2015 to 2020[J]. Environmental Science, 2022, 43(2): 675-685.
[35] 步巧利, 余乐福, 陈辰. 广州2014—2019年气象条件对O3污染影响的定量评估[J]. 干旱气象, 2022, 40(2): 266-274.
Bu Q L, Yu L F, Chen C. Quantitative assessment of influence of meteorological conditions on ozone pollution in Guangzhou during 2014-2019[J]. Journal of Arid Meteorology, 2022, 40(2): 266-274.
[36] 沈路路, 王聿绚, 段雷. 神经网络模型在O3浓度预测中的应用[J]. 环境科学, 2011, 32(8): 2231-2235.
Shen L L, Wang Y X, Duan L. Application of artificial neural networks on the prediction of surface ozone concentrations[J]. Environmental Science, 2011, 32(8): 2231-2235.
[37] 宋娜, 徐虹, 毕晓辉, 等. 海口市PM2.5和PM10来源解析[J]. 环境科学研究, 2015, 28(10): 1501-1509.
Song N, Xu H, Bi X H, et al. Source apportionment of PM2.5 and PM10 in Haikou[J]. Research of Environmental Sciences, 2015, 28(10): 1501-1509.
[38] 朱景, 袁慧珍. ERA再分析陆面温度资料在浙江省的适用性[J]. 气象科技, 2019, 47(2): 289-298.
Zhu J, Yuan H Z. Applicability of ERA reanalysis data of land surface temperature in Zhejiang Province[J]. Meteorological Science and Technology, 2019, 47(2): 289-298.
[39] 蒋维楣, 孙鉴泞, 曹文俊, 等. 空气污染气象学教程[M]. 北京: 气象出版社, 2004.
[40] 耿一超, 田春艳, 陈晓阳, 等. 珠江三角洲秋季臭氧干沉降特征的数值模拟[J]. 中国环境科学, 2019, 39(4): 1345-1354.
Geng Y C, Tian C Y, Chen X Y, et al. Numerical simulation of ozone dry deposition characteristics in autumn over the Pearl River delta region, China[J]. China Environmental Science, 2019, 39(4): 1345-1354. DOI:10.3969/j.issn.1000-6923.2019.04.001
[41] 陈璇, 王晓玲, 陈赛男, 等. 不同天气型下武汉城市圈PM2.5污染及大气层结特征分析[J]. 环境科学学报, 2022, 42(8): 52-63.
Chen X, Wang X L, Chen S N, et al. Characteristics of PM2.5 pollution and atmospheric stratification in Wuhan metropolitan area under different weather types[J]. Acta Scientiae Circumstantiae, 2022, 42(8): 52-63.