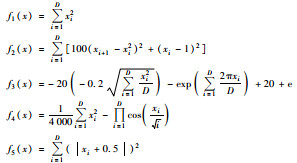2. 湖北经济学院工商管理学院, 武汉 430205;
3. 中南财经政法大学工商管理学院, 武汉 430073
2. School of Business Administration, Hubei University of Economics, Wuhan 430205, China;
3. School of Business Administration, Zhongnan University of Economics and Law, Wuhan 430073, China
当前, 人类社会正面临前所未有的能源危机与气候变化问题, 如何保证能源安全和应对气候治理, 实现可持续发展, 已成为全球建设人类命运共同体的光荣使命.改革开放至今, 我国在取得举世瞩目经济成就的同时, 已成为全球能源消费与碳排放量最大的国家[1, 2].我国政府对能源危机及气候治理问题的应对策略及政策力度, 短期内能源消费及碳排放规模如何, 已成为聚焦全世界目光的热点议题[3~7].习近平总书记2020年在75届联合国大会上宣布中国力争2030年前碳达峰, 2060年前碳中和.总体看, 我国的经济体量大、人口多、能源效率低、产业结构偏重和工业化城镇化尚未完全实现, 人们对美好生活向往的期许还在持续增长.这诸多现实因素决定了在未来较长时间内, 我国对能源的需求仍将保持刚性增长, 尤其高碳化的能源消费结构为2030年碳达峰目标带来巨大挑战[8~12].因此, 准确预测能源消费及碳排放量可为我国合理制定能源和碳排政策, 科学有序落实双碳目标提供理论依据, 具有重要研究意义.
截至目前, 国内外学者提出的能源需求预测方法大致可分成3大类: 单一预测方法(灰色模型[13]、自回归模型[14]、支持向量机[15]、模糊理论[16]、贝叶斯方法[17]、情景分析法[18]、神经网络[19]、马尔可夫模型[20]、德尔菲方法[21]、线性回归模型[22]和指数平滑模型[23]等)、组合预测方法[24~27]及基于时序数据“分解-集成”策略的预测方法[28~31].从建模数据集的视角看, 单一预测方法和组合预测方法在待预测时间序列的整体数据尺度上构建模型, 难以全面捕捉能源需求受主导因素影响的趋势成分和具有较强随机性及非线性特征的非趋势成分演化规律, 导致某些情景下预测性能难以取得理想效果.为了有效解决上述问题, 学者们引入一种基于时序数据分解的“分解-集成”策略预测方法: 通过数据分解技术, 将原始复杂时序分解为若干相对简单的细分子序列, 分别建立模型预测, 通过相加集成方法求取能源需求预测值.从文献[28~31]可知: ①“分解-集成”策略将原始复杂预测问题转化为若干相对简单的子序列预测问题, 减少了建模时待预测时序的波动性和非线性, 提升了预测精度; ②与单层“分解-集成”方法相比, 两层“分解-集成”方法通过更深层次的二次分解, 进一步降低了待预测问题的复杂度, 捕捉能源需求演化规律的能力更强, 预测精度更高.然而, 当前“分解-集成”预测模型中数据分解方法存在一些局限性, 导致其提取能源需求数据演化特征的能力受到限制, 以当前应用较为广泛的小波分解和经验模态分解为例进行说明: 小波分解具有多尺度分析能力, 能有效捕捉非线性特征时序演化规律, 但较难精确区分受主导因素影响的趋势项和较强随机性的非趋势项, 且小波函数和分解尺度难以确定, 导致某些场景下预测性能不理想; 经验模态分解是一种快速自适应分解算法, 但容易出现模态混叠问题, 且趋势序列和非趋势序列依然难以区分.针对过往的“分解-集成”预测方法难以有效区分趋势项和非趋势项的问题, 如何合理选择分解方法提取受主导因素影响的趋势项和波动性较强的非趋势项, 有待进一步研究.
基于上述背景和研究现状, 本文提出了一种两层“分解-集成”策略的预测模型, 充分利用了趋势分解(trend decomposition, TD)、经验模态分解(empirical mode decomposition, EMD)、融合位置扰动和模拟退火的改进粒子群算法(improved particle swarm optimization, IPSO)和长短期记忆神经网络(long short-term memory, LSTM)的优点, 预测性能获得显著提升.利用上述模型预测我国2021~2035年能源消费和碳排放量, 寻求落实2030年前碳达峰目标的有效途径, 以期为科学制定我国能源及碳排政策提供决策支持, 对于如期实现碳达峰碳中和“双碳”目标具有重要现实意义.
1 材料与方法 1.1 融合位置扰动和模拟退火的改进粒子群算法IPSO针对标准粒子群算法(particle swarm optimization algorithm, PSO)存在局部最优陷阱问题[32~34], 构建了一种融合位置扰动和模拟退火策略的改进粒子群算法IPSO.假设d维搜索空间中第i个粒子在t次迭代的速度和位置分别为vit=(vi, 1t, vi, 2t, …, vi, dt)和xit=(xi, 1t, xi, 2t, …, xi, dt); n为粒子数; pi, j为第i个粒子当前最优位置; pg, j为整个种群当前最优位置; r1和r2为随机数; fit()为适应度函数; c1和c2为学习因子; ω为惯性权重; t为迭代次数; i=(1, 2, …, n); j=(1, 2, …d); [Di, jLow, Di, jHigh]为搜索边界; γ为粒子位置更新权值(0≤γ≤1); η为退火常数.IPSO算法描述如下.
步骤1: 设置PSO参数, 随机初始化粒子位置和速度.
步骤2: 按照公式(1)调整越界粒子位置.

|
(1) |
粒子在迭代寻优时, 可能会飞出搜索边界.传统处理方法是将越界粒子位置映射到最近边界, 难免导致边界附近聚集大量粒子, 减弱粒子分布多样性, 容易陷入局部最优陷阱.因此, 这里引入公式(1)所示的越界粒子位置镜像映射方法, 有利于减少边界附近粒子聚集, 增强粒子多样性, 提高粒子群全局搜索能力.
步骤3: 根据fit()评价粒子适应值, 将粒子自身最优和种群全局最优存储在pi, j和pg, j.
步骤4: 设置模拟退火初始温度T0=fit(pg, j)/ln 5.
步骤5: 根据公式(2)计算当前温度T下pi, j的适配值TF().
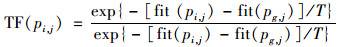
|
(2) |
步骤6: 利用轮盘赌策略从所有pi, j确定替代的全局最优pg, j.如果TF(pi, j)≥TF(pg, j), 则pg, j=pi, j; 如果TF(pi, j) < TF(pg, j), 则按照TF(pi, j)概率接受pg, j=pi, j.模拟退火算法在搜索过程中不但接受好解, 还以受温度参数控制的概率接受差解, 具备一定概率突跳能力, 有利于提高粒子跳出局部最优陷阱的能力.
步骤7: 按照公式(3)更新粒子速度.
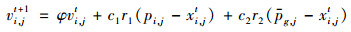
|
(3) |
其中:
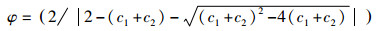
|
步骤8: 按照公式(4)更新粒子位置i, jt+1.
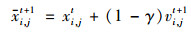
|
(4) |
为了减少粒子搜索步长过大而陷入局部最优陷阱的概率, 这里引入考虑历史位置影响的粒子位置更新权值γ.结合公式(4)和标准PSO的位置更新公式(5), 可推导出公式(6).从公式(6)可知: ① γ表示粒子位置更新过程中当前位置和历史位置的影响程度; ②当γ很小时, 粒子位置更新受历史位置影响较小, 收敛速度接近标准粒子群算法; ③ γ越大, 粒子位置更新受历史位置影响越大, 收敛速度越快; ④当粒子位置更新足够大时, 粒子位置更新受历史位置影响极大, 容易陷入局部最优陷阱.
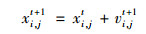
|
(5) |
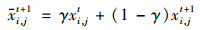
|
(6) |
步骤9: 按照公式(1)调整越界粒子位置.
步骤10: 根据fit()计算各粒子适应值, 若优于历史pi, j, 则用当前值更新pi, j; 比较全部粒子的pi, j和pg, j, 如果存在pi, j优于pg, j, 则更新pg, j.
步骤11: 按照公式(7)实施退火操作.
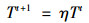
|
(7) |
步骤12: 当全局最优呆滞计数器达到预设阈值时, 重新初始化粒子位置和速度.按照公式(1)调整越界粒子位置, 更新pi, j和pg, j, 增加迭代过程中呆滞粒子的多样性, 有利于提升粒子跳出局部最优陷阱的能力.
步骤13: 若满足预设搜索停止条件, 停止迭代并输出全局最优pg, j, 否则返回步骤5继续下一轮搜索.
为了检验构建的IPSO算法的综合性能, 选取表 1中5个测试函数进行搜索最优值的仿真实验.同时, 选择以下6种竞争粒子群算法作为性能对比: 标准粒子群算法PSO、利用收缩因子调整粒子群收敛趋势的改进算法PSO-CK[35]、具有自适应惯性权值和加速度系数切换延迟的改进算法SDPSO[36]、具有时变加速度系数的改进算法PSO-TVAC[37]、线性递减惯性权重的改进算法PSO-LDIW[38]和利用进化因子自适应选择惯性权重和加速度系数的改进算法SPSO[39].
|
|
表 1 测试函数 Table 1 Test functions |
粒子群算法测试仿真在MATLAB R2019a上连续运行50次, 统计测试函数寻优过程的最优值、平均值、标准差和成功率.IPSO仿真实验参数设置为: 粒子群数n为30; 学习因子c1和c2为2.0; 粒子位置更新权值γ为0.45; 退火常数η为0.3; 全局最优呆滞计数器阈值为500; 目标误差为0.001, 最大寻优迭代次数为20 000.由表 2所示的性能对比可知[35~40]: ① IPSO算法在测试函数优化解的均值、最小值、标准差和成功率方面均优于竞争粒子群算法; ② IPSO融合模拟退火和粒子位置扰动策略, 有效提高了粒子群多样性和分布均匀性, 具有收敛速度快、精度高、稳定性强和全局寻优能力强的特点.
|
|
表 2 不同PSO算法性能对比 Table 2 Different PSO performance comparison results |
1.2 基于两层“分解-集成”策略的预测模型
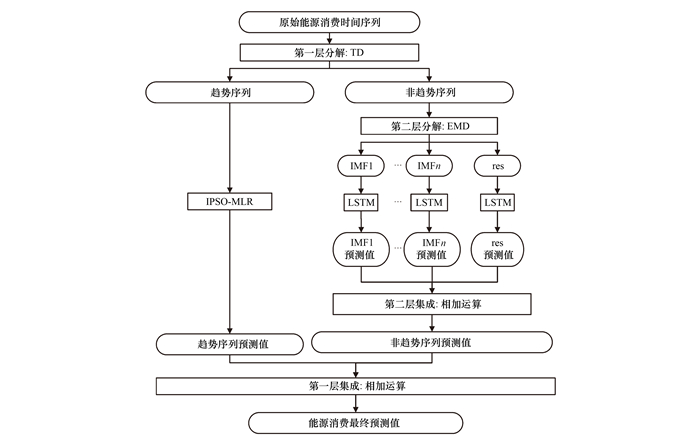
提出了一种基于TD-EMD两层“分解-集成”策略的预测模型(如图 1), 建模步骤如下.
|
图 1 基于TD-EMD两层“分解-集成”策略的IPSO-MLR-LSTM预测模型 Fig. 1 IPSO-MLR-LSTM forecasting model based on two-layer decomposition-ensemble approach using TD-EMD |
考虑到多元线性回归模型(multivariate linear regression, MLR)能有效捕捉时间序列中受主导影响因素决定的变化趋势, 且实施便捷, 这里选用MLR对能源消费时间序列实施趋势分解, 捕捉受主导因素影响的能源消费中趋势成分演化规律, 将能源消费时间序列分解为相对平稳的趋势项和复杂度较高的非趋势项.同时, 利用融合位置扰动和模拟退火的改进粒子群算法IPSO优化求解MLR的回归系数, 以提高求解速度和精度.假设原始能源消费时间序列为Y, 趋势分解后的趋势序列Ytrend和非趋势序列Ynon-trend如公式(8)所示, 公式(9)为能源消费的MLR预测模型.
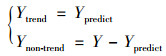
|
(8) |
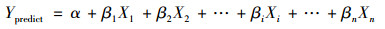
|
(9) |
式中, Xi为MLR自变量, 代表能源消费主要影响因素; n为自变量个数; Ypredict为MLR因变量, 表示能源消费的MLR模型预测值; α和βi为回归系数.
由上述公式可知, 趋势序列为能源消费整体演化趋势, 主要由能源消费结构、经济增长、人均生活能源消费水平、能源效率、产业结构和人口数量等影响因素决定; 非趋势序列为原始能源消费时间序列减去趋势序列后所得到的残差项, 它反映了具有较强波动性和非线性特征的非趋势性变化量.因此, 趋势分解具有比较明确的物理意义, 兼顾了影响因素和趋势项之间的对应关系, 有利于揭示受主要影响因素所决定的能源消费时间序列演化趋势.
1.2.2 利用EMD实现第二层分解在能源消费非趋势项整体数据尺度上建模, 难以充分捕捉具有较强波动性和非线性特征的非趋势成分的数据特征.考虑到EMD是一种快速自适应分解算法, 可实现非线性波动数据的平稳化处理.因此, 通过EMD对非趋势项展开第二层分解, 将其分解成若干个本征模态函数(intrinsic mode functions, IMFs)项和一个残差项res, 进一步降低能源消费非趋势项的复杂度.
1.2.3 预测子序列首先, 利用第一层分解中构建的MLR模型预测能源消费的趋势序列.其次, 鉴于LSTM是一种具有长短期记忆功能的改进循环神经网络, 通过独特的门控机制实现记忆及遗忘, 挖掘时间序列演化发展趋势, 对非线性映射具有较强的深度学习能力和长期依赖处理能力, 因此运用LSTM对第二层分解后的能源消费非趋势子序列独立建模预测.
1.2.4 通过相加集成方法求解最终预测值选择相加方法, 集成趋势项、非趋势项的IMFs项和残差项res预测值, 求取最终能源消费预测值.
1.3 碳排放测算方法碳达峰的“碳”是CO2, 主要指化石能源消费产生的CO2.假设化石能源使用过程中碳完全转化为CO2, 按照《2006年IPCC国家温室气体清单指南》IPCC系数法测算CO2排放量[41], 如公式(10)所示.
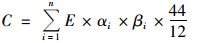
|
(10) |
式中, C为CO2排放量; E为能源消费总量; i为能源类型; n为能源类型数量; αi为第i类能源消费占比; βi为第i类能源的碳排放系数(如表 3).
|
|
表 3 不同种类能源的碳排放系数 Table 3 Carbon emission coefficients of different energy |
1.4 数据来源与处理
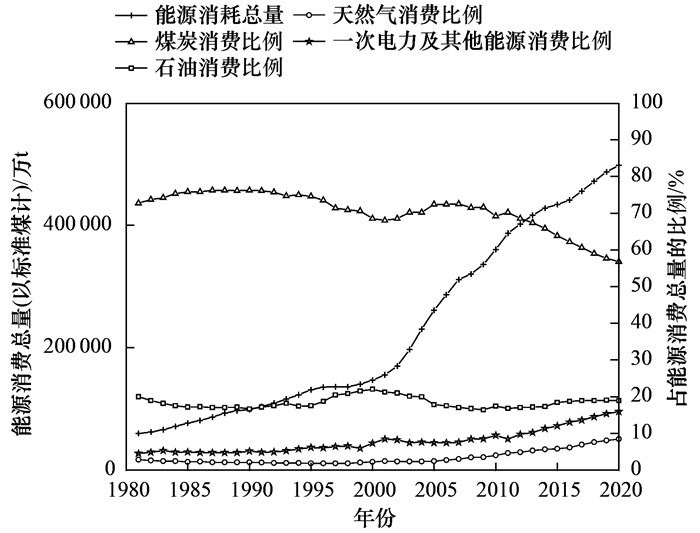
本文数据来源于《中国统计年鉴(2021年)》.从图 2所示的能源消费及构成可知: 在1981~2020年期间, 我国能源消费逐年增长, 能源消费结构以煤炭等化石能源为主, 能源消费时间序列呈现出较强波动性和非线性特征.
|
图 2 我国能源消费及构成 Fig. 2 China's annual energy consumption and energy structure |
根据能源需求演化趋势, 将其大致分成如下4个阶段[42, 43].
(1) 第一阶段(1981~1996年) 党的十一届三中全会拉开了改革开放大幕, 我国启动工业化和城市化进程, 能源消费以年均5.64%增速从1981年59 447万t(以标准煤计, 下同)增长到1996年135 192万t.在此阶段, 我国经济规模相对较小, 能源需求规模较低, 能源消费结构中煤炭和石油占比超过90%, 天然气和非化石能源等清洁能源处于起步阶段.
(2) 第二阶段(1997~2007年) 随着改革开发继续深入, 工业化和城市化进程加速, 我国能源需求迈入规模速度型阶段, 能源消费以年均8.02%增速从1997年135 909万t增长到2007年311 442万t.首先, 1997年爆发的亚洲金融危机导致能源消费年增长率从1996年3.06%下降到1997年0.53%和1998年0.2%.随后, 经济逐渐复苏, 能源需求增长提速.特别是我国2001年12月加入WTO后, 房地产和出口等领域大规模扩张, 能源需求迎来爆发式增长, 2002~2007年能源消费年均增速高达12.32%.在此阶段, 煤炭和石油消费占比依然高达90%左右, 清洁能源占比略有提升.
(3) 第三阶段(2008~2014年) 2008年世界金融危机爆发, 能源需求增速放缓, 能源消费以年均4.55%的增速从2008年320 611万t增长到2014年428 334万t.首先, 经济危机导致能源消费增速从2007年8.72%骤降到2008年2.94%.随后, 我国启动4万亿元经济刺激计划, 能源消费急速攀升, 2011年增速上升至7.32%.此后, 经济刺激影响力趋弱, 能源需求增速放缓, 2014年增速下降至2.74%.在此阶段, 天然气和非化石等清洁能源占比快速攀升.
(4) 第四阶段(2015~2020年) 我国坚持绿色可持续发展理念, 经济增长从以“高能耗、高污染、高排放”支撑的粗放式高速发展阶段转向高质量发展阶段, 能源需求增速放缓, 能源消费以年均2.55%增速从2015年434 112.8万t增长到2020年498 000万t.在此阶段, 为了保障能源安全和应对全球气候变暖问题, 我国能源消费结构中天然气和非化石能源等清洁能源占比显著提升, 煤炭消费占比明显下降, 能源消费结构的低碳清洁化调整提速.
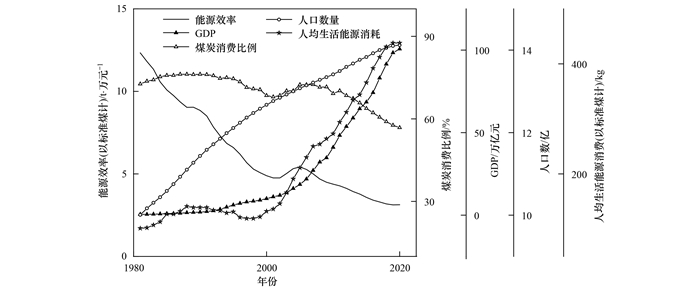
基于上述能源需求演化趋势, 本文建模数据的处理和检验如下: 首先, 对MLR的自变量和因变量取自然对数, 以减少异方差影响.其次, MLR建模的假设前提之一是噪声服从正态分布, 即因变量服从正态分布.经Kolmogorov-Smirnov检验, 能源消费时间序列在95%置信度水平下服从正态分布.然后, 借鉴文献[44, 45]的检验分析, 为了减少候选自变量共线性对MLR模型性能的影响, 选择能源消费结构(以煤炭消费比例代替)、国内生产总值(gross domestic product, GDP)、人口数量、能源效率(以万元国内生产总值能源消费量代替)和人均生活能源消费作为自变量(如图 3).
|
图 3 能源消费MLR模型的自变量 Fig. 3 Independent variables of energy consumption MLR model |
选择平均绝对值百分比误差MAPE、均方根误差RMSE和Theil不等系数TIC作为模型预测性能的评价指标, 如公式(11)~(13)所示.MAPE、RMSE和TIC越小, 表示预测精度越高和稳定性越好.
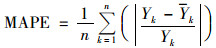
|
(11) |
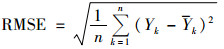
|
(12) |
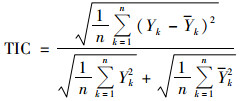
|
(13) |
式中, Yk为k时刻的能源消费真实值; k为k时刻的能源消费预测值; n为样本数; k为采样时刻.
1.5 预测情景构建 1.5.1 情景1情景1为基准情景, 根据我国“十四五”规划、《“十四五”现代能源体系规划》和《2030年前碳达峰行动方案》, 情景1设置如表 4~6所示.
|
|
表 4 情景1的变量年均增长率/% Table 4 Annual mean growth rate of variables under scenarios 1/% |
|
|
表 5 情景1的能源消费结构在2025、2030和2035年取值/% Table 5 Energy consumption structure at 2025, 2030 and 2035 under scenarios 1/% |
|
|
表 6 情景1的其它变量在2025、2030和2035年取值 Table 6 Other variables at 2025, 2030 and 2035 under scenarios 1 |
(1) 能源消费结构我国正大力推进非化石能源替代煤炭消费, 合理调控油气消费, 加快能源绿色低碳转型.《2030年前碳达峰行动方案》和《“十四五”现代能源体系规划》提出非化石能源消费比例在2025年和2030年达到20%和25%左右, 2035年继续大幅提高.考虑到我国“富煤、贫油、少气”的资源格局, 石油和天然气对外依赖程度较高, 从石油和天然气进口渠道安全可靠性考虑, 按2020年水平设置2021~2035年石油和天然气消费比例.
(2) 经济增长我国经济增长由高速增长阶段转向高质量发展阶段, 设置GDP在2021~2025、2026~2030和2031~2035期间年均增速为6%、5%和4%.
(3) 人口数鉴于育龄妇女人数逐渐减少, 生育年龄相对推后和养育成本日益提升等原因, 我国人口增长率已处于逐年下降趋势, 但暂未达到峰值, 仍将在未来一段时期内保持增长.因此, 设置人口在2021~2025、2026~2030和2031~2035期间年均增速为0.15%、0.1%和0.08%.
(4) 能源效率提升能源效率是降低能源消耗和碳排放的重要举措之一, 《2030年前碳达峰行动方案》提出, 单位GDP能源消耗2025年比2020年下降13.5%.早期能源效率偏低, 提升相对容易, 但在能源效率达到一定高度后, 进一步提升就比较困难.因此, 假设单位GDP能源消耗2025年比2020年下降13.5%, 则该阶段年均增速为-3.478%, 设置2026~2030和2031~2035期间年均增速为-2%和-1.5%.
(5) 人均生活能源消费一方面, 人民日益增长的美好生活需要促使人均生活能源消费量持续增长; 另一方面, 节能减排增效的绿色生活方式对人均生活能源消费量增长有抑制功能.设置人均生活能源消费在2021~2025、2026~2030和2031~2035期间年均增速为5%、3%和1%.
1.5.2 情景2在基准情景基础上, 按表 7设置GDP年均增速分别提高0.25%、0.5%、0.75%和1%.
|
|
表 7 情景2的GDP年均增长率/% Table 7 Annual mean growth rate of GDP under scenarios 2/% |
1.5.3 情景3
在基准情景基础上, 按表 8设置非化石能源消费比例年均增速分别提高0.1%、0.2%、0.3%和0.4%.
|
|
表 8 情景3的非化石能源消费比例年均增长率/% Table 8 Annual mean growth rate of the proportion of non-fossil energy consumption under scenarios 3/% |
1.5.4 情景4
在基准情景基础上, 按表 9设置人口数年均增速分别提高0.025%、0.05%、0.075%和0.1%.
|
|
表 9 情景4的人口数年均增长率/% Table 9 Annual mean growth rate of population under scenarios 4/% |
1.5.5 情景5
在基准情景基础上, 按表 10设置能源效率年均增速分别提高0.1%、0.2%、0.3%和0.4%.
|
|
表 10 情景5的能源效率年均增长率/% Table 10 Annual mean growth rate of energy efficiency under scenarios 5/% |
1.5.6 情景6
在基准情景基础上, 按表 11设置人均生活能源消费年均增速分别提高0.1%、0.2%、0.3%和0.4%.
|
|
表 11 情景6的人均生活能源消费年均增长率/% Table 11 Annual mean growth rate of household energy consumption per capita under scenarios 6/% |
2 结果与讨论 2.1 预测模型性能分析
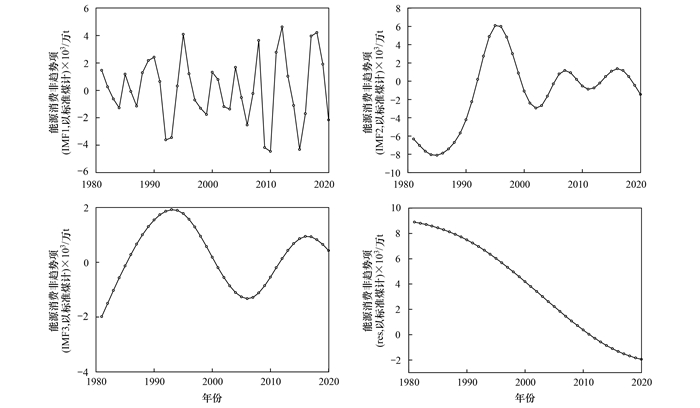
基于TD-EMD两层“分解-集成”策略的能源消费预测模型的实现: ①选择能源消费结构、GDP、人口数、能源效率和人均生活能源消费作为MLR自变量, 通过IPSO优化求解MLR回归系数(如表 12), 利用IPSO-MLR实施第一层TD分解, 将能源消费分解成趋势项和非趋势项(如图 4); ②对非趋势项实施第二层EMD分解, 将其进一步分解成3个本征模态函数项IMF1、IMF2、IMF3和残差项res(如图 5); ③利用IPSO-MLR预测能源消费趋势项, 运用LSTM对IMF1、IMF2、IMF3和res独立建模预测(LSTM采用输入层、隐含层和输出层的拓扑结构, 神经元数分别为1、32和1); ④选用相加集成上述子序列预测值, 求取最终能源消费预测值.
|
|
表 12 MLR回归系数 Table 12 MLR regression coefficients |

|
图 4 能源消费的TD分解结果 Fig. 4 TD results of energy consumption |
|
图 5 能源消费非趋势项的EMD分解结果 Fig. 5 EMD results of energy consumption non-trend subseries |
为了验证上述模型的有效性, 选取我国1981~2015年能源消费数据作为训练集构建模型, 2016~2020年能源消费数据作为测试集检验模型预测性能.同时, 选择单一预测模型(IPSO-MLR, LSTM), 组合预测模型(基于最优权值构建的IPSO-MLR和LSTM组合模型, 记为CM), 基于TD单层“分解-集成”策略的预测模型(趋势项用IPSO-MLR预测, 非趋势项在整体数据尺度上构建LSTM模型预测)作为参照模型.根据表 13汇总的上述不同模型预测能源消费的统计结果, 可得如下内容.
|
|
表 13 不同模型预测性能 Table 13 Prediction performance using different models |
(1) 单一预测模型IPSO-MLR和LSTM, 组合预测模型CM, 基于TD单层“分解-集成”策略的预测模型、基于TD-EMD两层“分解-集成”策略的预测模型MAPE分别为0.612%、1.595%、0.595%、0.554%和0.29%, 这表明上述模型均有较高预测精度, 能够较好预测能源消费.
(2) 组合预测模型CM的性能优于单一预测模型(IPSO-MLR, LSTM), 这表明组合模型能够更全面地利用各个单一模型所提供的有效信息, 捕捉能源消费时间序列演化趋势的能力更强, 预测精度得以提升.
(3)“分解-集成”模型性能优于单一模型和组合模型, 这说明“分解-集成”利用时序分解技术, 将复杂能源消费预测问题转化为若干相对简单子序列预测问题, 降低了问题复杂度, 提升了预测性能.
(4) 与单层TD“分解-集成”方法在能源消费非趋势项整体数据尺度上建模相比, 两层TD-EMD“分解-集成”方法采用了更深层次的二次分解策略, 将复杂的非趋势项经EMD分解为相对更简单的子序列, 进一步降低了非趋势项的复杂性和非平稳性, 捕捉能源消费非趋势项特征的能力更强.另外, 单层TD模型和两层TD-EMD模型预测非趋势项的Theil不等系数TIC分别为0.652和0.177, 这验证了上述结论.
(5) 与参照模型相比, 基于TD-EMD两层“分解-集成”策略的预测模型性能最优, 更全面地捕捉到能源消费趋势项和非趋势项演化趋势, 预测性能得以有效提升, 将其应用于能源消费预测是可行且有效的.
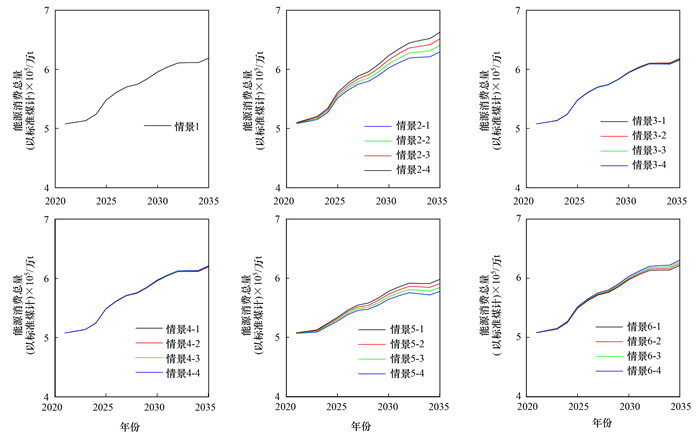
2.2 能源消费预测结果与分析按照构建的预测情景, 利用基于TD-EMD两层“分解-集成”策略的IPSO-MLR-LSTM模型, 预测我国2021~2035年能源消费总量(如图 6), 从预测结果可知如下内容.
|
图 6 中国能源消费预测(2021~2035年) Fig. 6 China's energy consumption prediction results from 2021 to 2035 |
(1) 对于全部情景, 我国能源消费总量在2021~2035年期间呈现持续增长态势.
(2) 作为基准情景的情景1, 能源消费(以标准煤计, 下同)从2020年的498 000万t增加到2035年的618 782.8万t, 2021~2035期间年均增速为1.458%, 低于2006~2020期间年均增速4.39%.随着碳达峰碳中和行动扎实推进, 我国经济增长从高速发展阶段转向高质量发展阶段, 通过合理控制能源消费总量, 推动能源消费革命, 能源消费增速放缓.
(3) 情景2的2-1~2-4中, 随着GDP年均增速按0.25%步长提高, 能源消费年均增速分别为1.575%、1.691%、1.808%和1.924%, 经济增长推动能源消费需求增长.
(4) 情景3的3-1~3-4中, 随着非化石能源消费比例年均增速按0.1%步长提高, 能源消费年均增速分别为1.45%、1.442%、1.433%和1.424%, 能源低碳转型对能源消费有抑制作用.
(5) 情景4的4-1~4-4中, 随着人口数年均增速按0.025%步长提高, 能源消费年均增速分别为1.465%、1.471%、1.478%和1.485%, 人口增长对能源消费有拉动效应.
(6) 情景5的5-1~5-4中, 随着能源效率年均增速按0.1%步长提高, 能源消费年均增速分别为1.225%、1.147%、1.068%和0.99%, 能源效率提升促进能源消费总量控制.
(7) 情景6的6-1~6-4中, 随着人均生活能源消费年均增速按0.1%步长提高, 能源消费年均增速分别为1.491%、1.523%、1.555%和1.587%.我国人口基数大, 人均生活能源消费水平增长会导致能源消费需求增长.
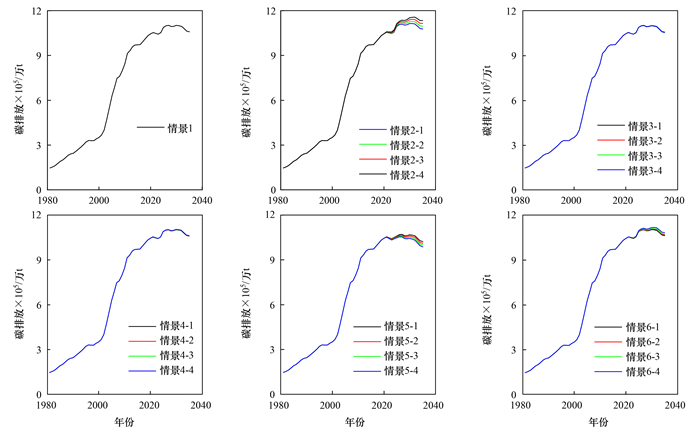
2.3 碳排放预测结果与分析不同情景下我国2021~2035年CO2排放量变化情况如图 7所示, 表 14描述了碳排放年均增速、碳达峰时间和峰值. 根据碳排放预测结果可知如下内容.
|
图 7 中国碳排放预测(2021~2035年) Fig. 7 China's carbon emission prediction results from 2021 to 2035 |
|
|
表 14 不同情景下碳达峰时间和峰值 Table 14 Carbon peak time and peak value under different scenarios |
(1) 在碳达峰碳中和的重大战略决策下, 我国能源消费产生的CO2排放量在本文构建的绝大多数情景中实现了2030年前碳达峰目标, 仅情景2-2~2-4和情景6-4的碳达峰时间在2030年之后.
(2) 作为基准情景的情景1, 碳达峰时间为2027年, CO2排放量峰值为1 101 450万t.碳排放年均增速从2011~2015年的2.9%下降到2021~2025年的0.83%、2026~2030年的-0.23%和2031~2035年的-0.77%.随着碳达峰贯穿于经济社会发展的全过程, 碳排放得到合理控制, 增速放缓.
(3) 情景2的2-1~2-4碳达峰时间和CO2排放量峰值分别为2030年和1 113 874万t、2031年和1 127 582万t、2031年和1 141 684万t、2032年和1 156 714万t.与基准情景相比, 随着GDP增速提高, 在一定程度上推迟了碳达峰时间, 增加了峰值, 经济增长对碳排放增长有拉动效应.
(4) 情景3的3-1~3-4中, 随着非化石能源消费比例年均增速按0.1%幅度提高, 碳达峰时间为2027年, 峰值与基准情景相比有所下降.加快实施低碳能源特别是非化石能源替代煤炭消费, 有望提前碳达峰时间窗口和降低碳达峰峰值.
(5) 情景4的4-1~4-4中, 碳达峰时间为2027年, 随着人口数量的增长, 碳达峰峰值上升.
(6) 情景5的5-1~5-4的碳达峰时间和CO2排放量峰值分别为2027年和1 070 689万t、2027年和1 064 926万t、2026年和1 059 413万t、2026年和1 054 504万t.节能增效是降低碳排放的重要途径, 能效水平的进一步提高有利于我国更顺利的实现碳达峰碳中和目标.
(7) 情景6的6-1~6-4的碳达峰时间和CO2排放量峰值分别为2030年和1 104 719万t、2030年和1 108 186万t、2030年和1 111 660万t、2031年和1 118 864万t.合理控制人均生活能源消费水平有利于实现碳达峰.
(8) 我国立足新发展阶段, 贯彻新发展理念, 选择科学有序“削峰”的碳达峰路径, 服务和融入新发展格局, 符合推动我国高质量发展战略的内在要求.
3 政策建议推进碳达峰碳中和是党中央和国务院的重要战略决策, 符合我国经济社会高质量发展的内在要求.结合本文研究工作, 提出以下助力实现2030年前碳达峰目标的政策建议.
(1) 推进能源绿色低碳高质量发展.立足富煤贫油少气的基本国情, 我国能源结构绿色低碳调整不可能一蹴而就, 能源消费结构在未来一段时期内仍将以煤炭为主, 应推动煤炭清洁高效利用, 发展可再生能源.因此, 在保障国家能源安全和经济发展底线的前提下, 合理加快煤炭减量步伐, 大力发展风电和太阳能发电等新能源, 规范推动水电开发, 稳妥发展生物质发电和核电等清洁能源, 有序增加天然气消费, 提高非化石能源消费比例.坚持先立后破的原则, 传统化石能源有序退出需要建立在新能源安全可靠替代的基础之上, 科学有序地推进我国能源绿色低碳转型平稳过渡.
(2) 推动产业结构优化升级.严格控制“三高”行业, 加速淘汰低端落后产能, 提高第三产业比例, 合理降低第二产业比例, 大力发展大数据、云计算、量子技术、工业互联网、区块链、边缘计算、人工智能、高端技术制造、生物技术、新材料及新能源等战略性新兴产业, 加快推动传统产业结构绿色低碳转型和高质量发展.当然, 产业结构优化调整是一个复杂且长期的任务, 应该稳妥有序推动产业结构升级, 坚持绿色可持续发展理念, 在经济社会高质量发展中促进产业结构绿色低碳转型, 在产业结构绿色低碳转型中实现经济社会更高质量发展.
(3) 提高经济增长质量.党的十九大报告作出了我国经济增长进入“调速换挡期”, 力争提质增效, 已由高速增长阶段转向高质量发展阶段的重大判断.因此, 将碳达峰碳中和目标全面融入我国经济社会发展全局之中, 统筹好发展与减排, 在资源高效利用和绿色低碳发展的基础之上推动经济社会发展.同时, 在保持经济持续平稳健康增长的同时也应综合考虑资源环境约束, 坚持经济社会发展与资源生态环境和谐共生, 走生态优先和绿色低碳可持续高质量发展道路.
(4) 推广节能降碳增效.把节能降碳增效贯穿于我国经济社会发展的全过程, 分领域实施节能降碳增效行动, 完善能源消费总量和能源消耗强度的双控制度, 落实节约优先原则, 提升节能减排管理水平; 推进煤电、有色金属、钢铁、石化石油、建材等重要行业节能减排增效升级改造, 提高能源利用效率; 采取更加严格的能效标准和节能要求, 提升泵、风机、锅炉等重点耗能设备的能效水平; 发挥科技创新的支撑引领作用, 强化节能减排增效领域基础研究, 加快关键核心技术和装备的科技攻关, 促进相关先进适用技术成果推广和应用.
(5) 推进绿色低碳全民行动.开展碳达峰碳中和宣传教育, 树立全民绿色低碳意识和生态文明理念, 增强节约意识, 遏制浪费和不合理消费, 倡导节约用能和减排, 大力发展绿色消费, 推广绿色低碳文明健康的生活方式.当前, 我国仍处于工业化城市化后期深化发展阶段, 人民日益增长的美好生活需要使得人均生活能源消费还有较大提升空间, 推进全民绿色低碳行动可有效降低全民终端能源消费和碳排放强度.同时, 全民绿色低碳生活方式对企业有重要导向作用, 引导企业低碳绿色转型, 推进节能降碳.
4 结论(1) 提出了一种融合位置扰动和模拟退火的IPSO算法, 增加了粒子群的多样性、分布均匀性和自适应跳动性, 有效克服了传统粒子群算法局部最优陷阱问题, 提高了收敛速度和精度.
(2) 构建了一种基于TD-EMD两层“分解-集成”策略的IPSO-MLR-LSTM预测模型, 将复杂预测问题转化为若干相对简单的子序列预测问题, 有效捕捉了能源消费演化规律, 提高了预测精度.
(3) 预测了不同情景下我国2021~2035年能源消费和碳排放量, 预测结果表明: ①能源消费总量维持增长态势, 增速明显放缓, 能源绿色低碳转型和节能降碳增效对能源消费有抑制作用; ②CO2排放量年均增速减缓, 坚持绿色可持续发展道路, 提高经济增长质量, 加快能源绿色低碳转型, 优化产业结构, 推广节能降碳增效, 引导全民绿色低碳生活, 有利于推动碳达峰时间窗口提前和峰值降低.
| [1] |
黄震, 谢晓敏, 张庭婷. "双碳"背景下我国中长期能源需求预测与转型路径研究[J]. 中国工程科学, 2022, 24(6): 8-18. Huang Z, Xie X M, Zhang T T. Medium-and long-term energy demand of China and energy transition pathway toward carbon neutrality[J]. Strategic Study of Chinese Academy of Engineering, 2022, 24(6): 8-18. |
| [2] |
刘华军, 石印, 郭立祥, 等. 新时代的中国能源革命: 历程、成就与展望[J]. 管理世界, 2022, 38(7): 6-23. Liu H J, Shi Y, Guo L X, et al. China's energy reform in the new era: process, achievements and prospects[J]. Journal of Management World, 2022, 38(7): 6-23. |
| [3] |
李辉, 庞博, 朱法华, 等. 碳减排背景下我国与世界主要能源消费国能源消费结构与模式对比[J]. 环境科学, 2022, 43(11): 5294-5304. Li H, Pang B, Zhu F H, et al. Comparative energy consumption structure and mode between China and major energy-consuming countries under the background of carbon emission reduction[J]. Environmental Science, 2022, 43(11): 5294-5304. DOI:10.13227/j.hjkx.202112065 |
| [4] |
宋苑震, 曾坚, 王森, 等. 中国县域碳排放时空演变与异质性[J]. 环境科学, 2023, 44(1): 549-559. Song Y Z, Zen J, Wang S, et al. Spatial-temporal evolution and heterogeneity of carbon emissions at county-level in China[J]. Environmental Science, 2023, 44(1): 549-559. DOI:10.13227/j.hjkx.202202137 |
| [5] |
蒋昀辰, 钟苏娟, 王逸, 等. 全国各省域碳达峰时空特征及影响因素[J]. 自然资源学报, 2022, 37(5): 1289-1302. Jiang Y C, Zhong S J, Wang Y, et al. Spatio-temporal characteristics and influencing factors of carbon emission peak by province of China[J]. Journal of Natural Resources, 2022, 37(5): 1289-1302. |
| [6] |
禹湘, 娄峰, 谭畅. 基于CIE-CEAM模型的中国工业"双碳"路径模拟[J]. 中国人口. 资源与环境, 2022, 32(7): 49-56. Yu X, Lou F, Tan C. A simulation study of the pathway of achieving the 'dual carbon' goals in China's industrial sectors based on the CIE-CEAM model[J]. China Population Resources and Environment, 2022, 32(7): 49-56. |
| [7] |
杨柏, 秦广鹏, 邬钦. "双碳"目标下中国省域碳排放核算分析[J]. 环境科学, 2022, 43(12): 5840-5849. Yang B, Qin G P, Wu Q. Analysis of provincial CO2emission accounting in China under the carbon peaking and carbon neutrality goals[J]. Environmental Science, 2022, 43(12): 5840-5849. |
| [8] |
岳立, 曹雨暄, 王宇. 能源政策的区域碳减排效应[J]. 资源科学, 2022, 44(6): 1105-1118. Yue L, Cao Y X, Wang Y. Effect of energy policies on regional carbon emission reduction[J]. Resources Science, 2022, 44(6): 1105-1118. |
| [9] |
薛英岚, 张静, 刘宇, 等. "双碳"目标下钢铁行业控煤降碳路线图[J]. 环境科学, 2022, 43(10): 4392-4400. Xue Y L, Zhang J, Liu Y, et al. Roadmap of coal control and carbon reduction in the steel industry under the carbon peak and neutralization target[J]. Environmental Science, 2022, 43(10): 4392-4400. |
| [10] |
王兴民, 吴静, 白冰, 等. 中国CO2排放的空间分异与驱动因素——基于198个地级及以上城市数据的分析[J]. 经济地理, 2020, 40(11): 29-38. Wang X M, Wu J, Bai B, et al. Spatial differentiation and driving factors of CO2 emissions: analysis based on 198 cities at prefecture level and above in China[J]. Economic Geography, 2020, 40(11): 29-38. |
| [11] |
张悦, 王晶晶, 程钰. 中国工业碳排放绩效时空特征及技术创新影响机制[J]. 资源科学, 2022, 44(7): 1435-1448. Zhang Y, Wang J J, Cheng Y. Spatiotemporal characteristics of China's industrial carbon emission performance and influence mechanism of technological innovation[J]. Resources Science, 2022, 44(7): 1435-1448. |
| [12] |
刘燕华, 李宇航, 王文涛. 中国实现"双碳"目标的挑战、机遇与行动[J]. 中国人口·资源与环境, 2021, 31(9): 1-5. Liu Y H, Li Y H, Wang W T. Challenges, opportunities and actions for China to achieve the targets of carbon peak and carbon neutrality[J]. China Population, Resources and Environment, 2021, 31(9): 1-5. |
| [13] | Duan H M, Jiang X C, He X Q, et al. A novel multivariate grey model of energy consumption under carbon trading background and its application[J]. Energy Reports, 2022, 8: 11952-11964. DOI:10.1016/j.egyr.2022.09.038 |
| [14] | Xu W Q, Peng H, Zeng X Y, et al. Deep belief network-based AR model for nonlinear time series forecasting[J]. Applied Soft Computing, 2019, 77: 605-621. DOI:10.1016/j.asoc.2019.02.006 |
| [15] | Xu L, Hou L, Zhu Z Y, et al. Mid-term prediction of electrical energy consumption for crude oil pipelines using a hybrid algorithm of support vector machine and genetic algorithm[J]. Energy, 2021, 222. DOI:10.1016/j.energy.2021.119955 |
| [16] | Torrini F C, Souza R C, Oliveira F L C, et al. Long term electricity consumption forecast in Brazil: a fuzzy logic approach[J]. Socio-Economic Planning Sciences, 2016, 54: 18-27. DOI:10.1016/j.seps.2015.12.002 |
| [17] | Yuan X C, Sun X, Zhao W G, et al. Forecasting China's regional energy demand by 2030: a Bayesian approach[J]. Resources, Conservation and Recycling, 2017, 127: 85-95. DOI:10.1016/j.resconrec.2017.08.016 |
| [18] | Hao H, Liu Z W, Zhao F Q, et al. Scenario analysis of energy consumption and greenhouse gas emissions from China's passenger vehicles[J]. Energy, 2015, 91: 151-159. DOI:10.1016/j.energy.2015.08.054 |
| [19] | Tian Y, Yu J Q, Zhao A J. Predictive model of energy consumption for office building by using improved GWO-BP[J]. Energy Reports, 2020, 6: 620-627. |
| [20] | Munkhammar J, Van Der Meer D, Widén J. Very short term load forecasting of residential electricity consumption using the Markov-chain mixture distribution (MCM) model[J]. Applied Energy, 2021, 282. DOI:10.1016/j.apenergy.2020.116180 |
| [21] | Varho V, Rikkonen P, Rasi S. Futures of distributed small-scale renewable energy in Finland-a Delphi study of the opportunities and obstacles up to 2025[J]. Technological Forecasting and Social Change, 2016, 104: 30-37. DOI:10.1016/j.techfore.2015.12.001 |
| [22] | Ciulla G, D'Amico A. Building energy performance forecasting: a multiple linear regression approach[J]. Applied Energy, 2019, 253. DOI:10.1016/j.apenergy.2019.113500 |
| [23] | Maçaira P M, Souza R C, Oliveira F L C. Modelling and forecasting the residential electricity consumption in Brazil with Pegels exponential smoothing techniques[J]. Procedia Computer Science, 2015, 55: 328-335. DOI:10.1016/j.procs.2015.07.057 |
| [24] | Li J R, Wang R, Wang J Z, et al. Analysis and forecasting of the oil consumption in China based on combination models optimized by artificial intelligence algorithms[J]. Energy, 2018, 144: 243-264. DOI:10.1016/j.energy.2017.12.042 |
| [25] | Zhang Y C, Le J, Liao X B, et al. A novel combination forecasting model for wind power integrating least square support vector machine, deep belief network, singular spectrum analysis and locality-sensitive hashing[J]. Energy, 2019, 168: 558-572. DOI:10.1016/j.energy.2018.11.128 |
| [26] | Dong Y Q, Wang J Z, Wang R, et al. Accurate combination forecasting of wave energy based on multiobjective optimization and fuzzy information granulation[J]. Journal of Cleaner Production, 2023, 386. DOI:10.1016/j.jclepro.2022.135772 |
| [27] | Yuan Z, Wang W Q, Wang H Y, et al. Combination of cuckoo search and wavelet neural network for midterm building energy forecast[J]. Energy, 2020, 202. DOI:10.1016/j.energy.2020.117728 |
| [28] | Xia C, Wang Z. Drivers analysis and empirical mode decomposition based forecasting of energy consumption structure[J]. Journal of Cleaner Production, 2020, 254. DOI:10.1016/j.jclepro.2020.120107 |
| [29] |
谢小瑜, 周俊煌, 张勇军, 等. 基于W-BiLSTM的可再生能源超短期发电功率预测方法[J]. 电力系统自动化, 2021, 45(8): 175-184. Xie X Y, Zhou J H, Zhang Y J, et al. W-BiLSTM based ultra-short-term generation power prediction method of renewable energy[J]. Automation of Electric Power Systems, 2021, 45(8): 175-184. |
| [30] |
陈锦鹏, 胡志坚, 陈纬楠, 等. 二次模态分解组合DBiLSTM-MLR的综合能源系统负荷预测[J]. 电力系统自动化, 2021, 45(13): 85-94. Chen J P, Hu Z J, Chen W N, et al. Load prediction of integrated energy system based on combination of quadratic modal decomposition and deep bidirectional long short-term memory and multiple linear regression[J]. Automation of Electric Power Systems, 2021, 45(13): 85-94. |
| [31] | Liu H, Mi X W, Li Y F. Comparison of two new intelligent wind speed forecasting approaches based on wavelet packet decomposition, complete ensemble empirical mode decomposition with adaptive noise and artificial neural networks[J]. Energy Conversion and Management, 2018, 155: 188-200. DOI:10.1016/j.enconman.2017.10.085 |
| [32] | Xing Z Y, Zhu J L, Zhang Z Y, et al. Energy consumption optimization of tramway operation based on improved PSO algorithm[J]. Energy, 2022, 258. DOI:10.1016/j.energy.2022.124848 |
| [33] | Song B Y, Wang Z D, Zou L. An improved PSO algorithm for smooth path planning of mobile robots using continuous high-degree Bezier curve[J]. Applied Soft Computing, 2021, 100. DOI:10.1016/j.asoc.2020.106960 |
| [34] | Chen G G, Liu L L, Song P Z, et al. Chaotic improved PSO-based multi-objective optimization for minimization of power losses and L index in power systems[J]. Energy Conversion and Management, 2014, 86: 548-560. DOI:10.1016/j.enconman.2014.06.003 |
| [35] | Clerc M, Kennedy J. The particle swarm-explosion, stability, and convergence in a multidimensional complex space[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(1): 58-73. DOI:10.1109/4235.985692 |
| [36] | Zeng N Y, Wang Z D, Zhang H, et al. A novel switching delayed PSO algorithm for estimating unknown parameters of lateral flow immunoassay[J]. Cognitive Computation, 2016, 8(2): 143-152. DOI:10.1007/s12559-016-9396-6 |
| [37] | Ratnaweera A, Halgamuge S K, Watson H C. Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients[J]. IEEE Transactions on Evolutionary Computation, 2004, 8(3): 240-255. DOI:10.1109/TEVC.2004.826071 |
| [38] | Shi Y H, Eberhart R C. Parameter selection in particle swarm optimization[A]. Proceedings of the 7th International Conference on Evolutionary Programming[C]. San Diego: Springer, 1998.591-600. |
| [39] | Tang Y, Wang Z D, Fang J A. Parameters identification of unknown delayed genetic regulatory networks by a switching particle swarm optimization algorithm[J]. Expert Systems with Applications, 2011, 38(3): 2523-2535. DOI:10.1016/j.eswa.2010.08.041 |
| [40] |
王闯, 张勇, 李学贵, 等. 改进粒子群优化算法及其在聚类分析中应用[J]. 系统仿真学报, 2020, 32(8): 1577-1587. Wang C, Zhang Y, Li X G, et al. An improved particle swarm optimization algorithm and its application in clustering analysis[J]. Journal of System Simulation, 2020, 32(8): 1577-1587. DOI:10.16182/j.issn1004731x.joss.19-0006 |
| [41] |
郝瑞军, 魏伟, 刘春芳, 等. 中国能源消费碳排放的空间化与时空动态[J]. 环境科学, 2022, 43(11): 5305-5314. Hao R J, Wei W, Liu C F, et al. Spatialization and spatio-temporal dynamics of energy consumption carbon emissions in China[J]. Environmental Science, 2022, 43(11): 5305-5314. DOI:10.13227/j.hjkx.202112066 |
| [42] | Ma X J, Wang C X, Dong B Y, et al. Carbon emissions from energy consumption in China: Its measurement and driving factors[J]. Science of the Total Environment, 2019, 648: 1411-1420. DOI:10.1016/j.scitotenv.2018.08.183 |
| [43] | Wang Q, Song X X, Liu Y. China's coal consumption in a globalizing world: Insights from multi regional input-output and structural decomposition analysis[J]. Science of the Total Environment, 2020, 711. DOI:10.1016/j.scitotenv.2019.134790 |
| [44] |
柴建, 郭菊娥, 卢虎, 等. 基于Bayes误差修正的我国能源消费需求组合预测研究[J]. 中国人口·资源与环境, 2008, 18(4): 50-55. Chai J, Guo J E, Lu H, et al. Application of path analysis and combining forecasting in the forecast of energy demand in China[J]. China Population, Resources and Environment, 2008, 18(4): 50-55. |
| [45] |
张祖欣. 基于多变量误差修正模型与改进灰色理论的我国能源需求预测研究[J]. 华东电力, 2012, 40(10): 1685-1689. Zhang Z X. China's energy demand forecast based on multivariate error correction model and improved gray theory[J]. East China Electric Power, 2012, 40(10): 1685-1689. |
 2023, Vol. 44
2023, Vol. 44