环境科学  2021, Vol. 42 Issue (12): 5602-5615   PDF    
引用本文
吴宇宏, 杜宁, 王莉, 蔡宏, 周彬, 吴磊, 敖逍. 基于iLME+Geoi-RF模型的四川省PM2.5浓度估算[J]. 环境科学, 2021, 42(12): 5602-5615.
WU Yu-hong, DU Ning, WANG Li, CAI Hong, ZHOU Bin, WU Lei, AO Xiao. Estimation of PM2.5 Concentration in Sichuan Province Based on Improved Linear Mixed Effect Model and Geo-intelligent Random Forest[J]. Environmental Science, 2021, 42(12): 5602-5615.
基于iLME+Geoi-RF模型的四川省PM2.5浓度估算
吴宇宏, 杜宁, 王莉, 蔡宏, 周彬, 吴磊, 敖逍     
贵州大学矿业学院, 贵阳 550025
收稿日期: 2021-02-05; 修订日期: 2021-05-27
基金项目: 国家自然科学基金项目（41901225）
作者简介: 吴宇宏(1997~), 男, 硕士研究生, 主要研究方向为资源与环境遥感, E-mail: 1092254967@qq.com
通信作者: 杜宁, E-mail: ndu1@gzu.edu.cn
摘要: 高分辨率PM2.5空间分布数据对动态监测和控制PM2.5污染具有重要意义.选取Himawari-8气溶胶光学厚度（AOD）、ERA5气象再分析资料、DEM、土地利用数据、夜光遥感数据、增强型植被指数和人口数据等作为估算变量，使用改进的重采样法进行数据匹配，并提出改进的线性混合模型（iLME）结合地理智能随机森林（Geoi-RF）构建组合模型估算PM2.5浓度.结果表明：①在选取的估算变量中，气溶胶光学厚度、气压、温度、相对湿度和边界层高度是影响2016年四川省PM2.5浓度的重要因素，其相关系数分别为0.65、0.58、0.55、0.54和0.35.②iLME+Geoi-RF模型精度相较其他模型有较大提升，模型拟合R2、RMSR和MAE分别为0.98、3.25 μg·m-3和1.98 μg·m-3，交叉验证R2、RMSR和MAE分别为0.89、7.95 μg·m-3和4.81 μg·m-3.该模型可获取更高精度的四川省PM2.5时空分布特征，为区域空气质量评估、人体暴露风险评价和环境污染治理提供更加合理地科学参考.③2016年四川省PM2.5浓度存在显著的季节性差异，各季节PM2.5浓度大小关系为：冬季>秋季>春季>夏季.2016年四川省月均PM2.5浓度总体上呈先降后升的"Ⅴ"型趋势，最小值在6月，最大值在12月，8月和11月有微小起伏.在空间分布上四川省PM2.5浓度总体上呈东高西低和局部污染程度较高的特点，高值区主要分布在城市快速发展和人口密集的东部地区，低值区主要分布在经济发展落后和人口稀疏的西部地区.④虽然不同模型估算出的PM2.5浓度整体分布基本一致，但iLME+Geoi-RF模型能更准确有效地估算本研究区污染的空间分布.
关键词: PM2.5      Himawari-8 AOD      重采样      共线性诊断      iLME+Geoi-RF模型      时空变化     
Estimation of PM2.5 Concentration in Sichuan Province Based on Improved Linear Mixed Effect Model and Geo-intelligent Random Forest
WU Yu-hong , DU Ning , WANG Li , CAI Hong , ZHOU Bin , WU Lei , AO Xiao     
Mining College, Guizhou University, Guiyang 550025, China
Abstract: High-resolution PM2.5 spatial distribution data is of great significance for the dynamic monitoring and control of PM2.5 pollution. Himawari-8 AOD data, ERA5 meteorological reanalysis data, DEM, land-use data, and luminous remote-sensing data were selected as estimating variables, using an improved resampling method for data matching and an improved linear mixed model (iLME) combined with a Geo-intelligent random forest model to build the combined model for estimating PM2.5 concentration. The results showed that: ① Among the estimated variables selected, AOD, SP, TEMP, RH, and BLH were important factors affecting the PM2.5 concentration of Sichuan Province in 2016, and their correlation coefficients were 0.65, 0.58, 0.55, 0.54, and 0.35, respectively. ② The prediction accuracy of the iLME+Geoi-RF model was greatly improved compared to that of other models. The model-fitted R2, RMSR, and MAE were 0.94, 5.72 μg·m-3, and 3.92 μg·m-3, and the cross-validated R2, RMSR, and MAE were 0.82, 10.20 μg·m-3, and 6.44 μg·m-3, respectively. The model can obtain more accurate spatial and temporal distribution characteristics of PM2.5 in Sichuan Province and provide a more reasonable scientific reference for regional air quality assessment, human exposure risk assessment, and environmental pollution control. ③ There was a significant seasonal difference in PM2.5 concentration in Sichuan Province, with the highest concentration of PM2.5 in winter, followed by spring and autumn, with the concentration of PM2.5 in summer being the lowest. In 2016, the monthly average PM2.5 concentration in Sichuan Province showed a V shape that first decreased and then increased, with the minimum value in June, the maximum value in December, and slight fluctuations in August and November. In terms of spatial distribution, the PM2.5 concentration in the eastern area of Sichuan Province was generally higher than that in the west, and the local pollution level was relatively high. The high-valued areas were mainly distributed in the eastern region, where the cities have been developing rapidly and the population was densely distributed, whereas the low-valued areas were mainly distributed in the western region, where it is sparsely populated with backward economic development. ④ Although the overall distribution of PM2.5 concentration estimated by the different models was essentially the same, the iLME+Geoi-RF model could more accurately and effectively estimate the spatial distribution of pollution in this study area.
Key words: PM2.5      Himawari-8 AOD      resampling      collinearity diagnosis      iLME+Geoi-RF model      temporal and spatial changes     

细颗粒物(PM2.5)指空气动力学直径小于或等于2.5μm的颗粒[1], PM2.5对气候变化和人体健康等方面有许多不利影响[2], 已成为全社会关注的热点问题.中国建立地面空气质量监测网络监测PM2.5浓度, 但由于站点数量有限且分布不均, 无法获取连续的PM2.5浓度空间分布情况.与传统地面监测方法相比, 遥感监测具有覆盖率高和成本低等优点, 能有效弥补地面监测站点的不足, 可获得大区域尺度的污染物分布情况, 已被广泛用于PM2.5估算.

AOD是表征大气柱状气溶胶累积的基本参数[3], 已有研究表明AOD与PM2.5之间具有较高的相关性, 因此国内外许多学者利用AOD估算PM2.5浓度[4].①在数据处理方面, 需对不同空间分辨率的估算变量进行时空匹配, 目前大多采用最邻近插值[5]、双线性插值[6]、反距离权重插值[7]和克里格插值[8]等方法进行重采样, 但传统的插值往往会改变数据的真实信息.②在选取AOD数据方面, 目前大多研究使用MODIS传感器的AOD数据, 但MODIS每天仅能提供2次瞬时观测的AOD数据[9, 10], 较低的时间分辨率难以反映气溶胶光学厚度的真实分布.③在构建PM2.5估算模型方面, 早期利用AOD估算近地面PM2.5浓度多基于简单线性回归模型.比如Xin等[11]的研究建立简单线性回归模型拟合AOD-PM2.5之间的关系, 决定系数(R2)为0.49.考虑到AOD和PM2.5之间关系的时空异质性, 一些学者提出时空模型估算PM2.5浓度, 如线性混合(LME)模型[12]、地理加权回归(GWR)模型[13]和地理时间加权回归(GTWR)模型[14]等.为进一步研究AOD与PM2.5之间的非线性关系, 机器学习已取得丰富成果[15, 16].Hu等[17]的研究应用随机森林(RF)模型预测美国的PM2.5暴露水平. Chen等[18]的研究使用多元线性回归模型堆叠的3个机器学习子模型(AdaBoost、XGBoost和随机森林)估算中国中部和东部逐小时PM2.5浓度.但时空模型无法反映AOD与PM2.5间的非线性关系, 而机器学习对AOD-PM2.5关系的时空异质性考虑欠缺[19].

综上所述, 传统的PM2.5估算存在如下问题: ①插值方法会改变数据的真实信息.②从极轨卫星获取的AOD受到观测频率的限制, 不足以反映AOD的真实分布.③大多模型仅考虑AOD与PM2.5之间关系的时空异质性或非线性关系.针对以上问题, 本文以四川省为研究区域, 选取Himawari-8 AOD数据、ERA5气象再分析资料、土地利用数据、夜光遥感数据和增强型植被指数等作为估算变量, 使用改进的重采样法进行数据匹配, 并提出iLME结合Geoi-RF构建PM2.5估算模型, 估算了2016年季均和月均PM2.5浓度, 以期为区域空气质量评估、人体暴露风险评价和环境污染治理提供科学参考.

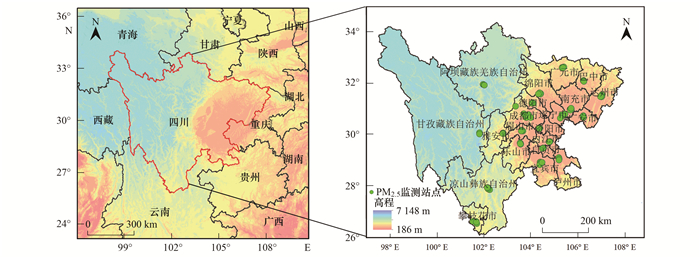
1 材料与方法 1.1 研究区域概况

四川省位于青藏高原和长江中下游平原的过渡地带, 总面积约48.6万km2, 介于97°~108°E和26°~34°N之间, 地势西高东低, 因其独特的地理位置, 风向受反气旋控制明显, 易形成明显的“回水区”或静风现象, 不利于污染物扩散, 加之四川盆地(主要包括四川省的成都、绵阳、泸州、南充、自贡、德阳、广元、遂宁、内江、乐山、宜宾、广安、达州、雅安、巴中、眉山和资阳, 贵州省的遵义和毕节, 云南省的昭通和重庆市等)边缘山地对空气的冷却作用, 使冷空气沿盆周向底部运动, 容易在盆地底部聚集, 形成典型的地形逆温现象, 造成污染物不断累积, 使得四川省中东部成为污染较为严重的地区.研究区域如图 1所示.

图 1 研究区域及地面监测站分布示意 Fig. 1 Research area and distribution of ground monitoring stations

1.2 数据来源及处理 1.2.1 PM2.5站点数据

PM2.5浓度数据来自2016年四川省94个空气质量监测站点实时发布的24 h连续监测数据, 通过中国国家环境监测中心(CNEMC, http://106.37.208.233:20035/)下载.经筛选后获得32 123个有效数据, 其中不包括异常数据(PM2.5>1 000 μg·m-3及PM2.5 < 0 μg·m-3).PM2.5监测站点分布见图 1.

1.2.2 Himawari-8 AOD数据

Himawari-8于2015年7月7日开始运行, 卫星覆盖范围为80°E~160°W和60°N~60°S, 每10 min进行1次观测[20], Zang等[21]的研究将Himawari-8 AOD与中国及其周边地区的42个AERONET站点的地面观测结果进行分析, 结果表明Himawari-8 AOD与AERONET实测AOD具有较高的相关性.故Himawari-8 AOD产品可用于地面PM2.5估算.Himawari-8 AOD产品包含4个置信度标识, 分别为“非常好”、“好”、“一般”和“不可靠”, 本文仅使用置信度为“非常好”的Level-3逐时AOD产品, 通过日本宇航局的P-Tree系统(http://www.eorc.jaxa.jp/ptree/)下载了2016年8784景影像.

1.2.3 气象数据

已有研究表明气象数据(如温度、风速、边界层高度和相对湿度)能有效提高AOD-PM2.5关联模型的精度[22].从欧洲中期天气预报中心(ECMWF)最新发布的ERA5再分析数据集(https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era5)获取2016年四川省一系列与PM2.5相关的气象数据, 包括边界层高度(BLH)、低植被覆盖指数(CVL)、气压(PS)、温度(TEMP)、总降水量(RAIN)、高植被覆盖指数(CVH)、10 m风速u分量(u10)、10 m风速v分量(v10)和相对湿度(RH).

1.2.4 其他数据

已有研究表明地理因素、植被指数、人口和城市经济因素是影响PM2.5浓度的重要因素[23].本文使用的2016年四川省土地利用数据、增强型植被指数及火点数据均来源于MODIS(https://ladsweb.modaps.eosdis.nasa.gov), 夜间灯光能较好地表征人类活动强度和能源消费状况, 是影响PM2.5浓度的重要因素, 夜光遥感数据来源于VIIRS(https://www.ngdc.noaa.gov/eog/viirs/download_dnb_composites.html), 人口数据来源于Gridded Population of the World, Version 4(GPWv4, http://sedac.ciesin.columbia.edu/data/collection/gpw-v4).DEM数据来源于航天飞机雷达地形任务(SRTM, http://srtm.csi.cgiar.org/srtmdata/).估算变量的具体信息见表 1.

表 1 估算变量的具体信息 Table 1 Specific information about estimated variables

1.2.5 数据匹配

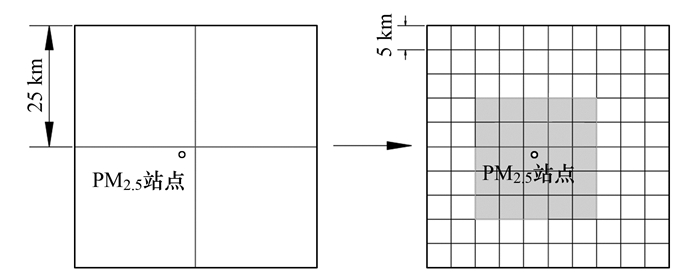
用于构建模型的数据集必须保持时间和空间上的一致性.时间上, 取卫星拍摄时刻前后1 h的PM2.5浓度均值与Himawari-8 AOD值进行匹配, 取与AOD拍摄时刻最邻近的ERA5数据作为Himawari-8拍摄时刻的气象数据.空间上, 以PM2.5监测站点为基准, 取像元中心位置距离监测站点最近的AOD像元为中心像元, 取中心像元25 km×25 km范围内的AOD均值代表卫星气溶胶.对于空间分辨率小于5 km的数据, 定位PM2.5站点所在的中心像元, 取中心像元25 km×25 km范围内的均值; 对于空间分辨率大于5 km的气象数据, 使用改进的重采样法对气象数据做降尺度处理, 再求取中心像元25 km×25 km范围内的平均值(如图 2).具体步骤: ①将空间分辨率为25 km的像元划分为5 km的25个像元; ②将原始像元值赋予新划分的像元; ③定位PM2.5站点所在的中心像元, 求取中心像元25 km×25 km范围内的均值.

图 2 改进的重采样示意 Fig. 2 Improved resampling diagram

1.3 模型构建与验证 1.3.1 共线性诊断

估算变量间的多重共线性会影响模型的性能, 故建模前应将存在多重共性的变量剔除.方差膨胀因子(VIF)是衡量自变量间多重共线性的重要指标[24], 其计算公式见式(1):

(1)

式中, Rμ2为自变量μ与其余自变量回归的相关系数.当VIF>10说明变量间存在多重共线性问题[25].各变量的VIF值见表 2, 其中SP(VIF=126.70)、TEMP(VIF=193.75)和RH(VIF=22.16)表现出严重的多重共线性, 经逐步回归后发现剔除TEMP和RH后, 其他变量的VIF值均小于5(表 2), 故除TEMP和RH外, 其他变量均加入iLME模型拟合.而机器学习具有强大的非线性映射能力, 无需考虑变量间的多重共线性问题, 故将TEMP和RH加入Geoi-RF模型拟合.

表 2 多重共线性检验结果 Table 2 Multicollinearity test results

1.3.2 改进的LME模型(ILME)

LME模型是线性回归模型的扩展, 由固定效应和随机效应组成.固定效应是常规的线性回归部分, 随机效应与随机抽取的实验个体相关.随机效应具有先验的正态分布, 均值为零且方差恒定[26, 27]. LME模型通过将共同的随机效应和具有相同水平的分组变量的观测值相关联来表示与数据分组有关的协方差结构.

但LME模型未考虑AOD与PM2.5之间关系的空间异质性, 不同的地理位置受到各种污染源、气象条件和人口密度等的影响, 都会影响LME模型的回归效果.考虑到AOD和PM2.5的关系在时间和空间上都会发生变化, 本文提出改进的LME模型, 在LME模型中嵌套包含地理加权系数的固定效应和随机效应, 以解释AOD和PM2.5之间关系的时空异质性, 其公式见式(2):

(2)

式中, PM2.5, i, j为第i天在第j个站点的PM2.5的平均浓度值; AODi, j、BLHi, j、CVLi, j、PSi, j、RAINi, j、CVHi, j、u10, i, j、v10, i, j、DEMi, j、LUCCi, j、NLi, j、EVIi, j、FPIi, j和POPi, j分别为第i天在第j个站点对应像元的气溶胶光学厚度、边界层高度、低植被覆盖指数、气压、降水量、高植被覆盖指数、10 m风速u分量、10 m风速v分量、高程、土地利用、夜间灯光指数、增强型植被指数、火点数量和人口密度; α0为固定截距; β0为固定斜率; α1~α14为随机截距; β1~β14为随机斜率; ε为误差项.w为地理加权系数, 其公式见式(3):

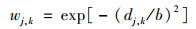
(3)

式中, dj, k为站点j和站点k之间的距离, b为描述权重与距离之间函数关系的非负衰减参数, 称为带宽.

1.3.3 地理智能随机森林(GEOI-RF)

随机森林通过bootstrap重采样技术, 从原始训练样本集中有放回地重复随机抽取样本生成新的训练样本集合进行决策树建模, 然后组合多棵决策树组成随机森林.与其他机器学习算法相比, 随机森林算法能处理高维度数据, 并且无需做特征选择, 具有对数据集的适应力强、实现简单、精度高和抗过拟合能力强等优势[28].

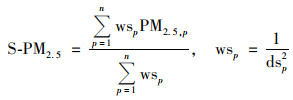
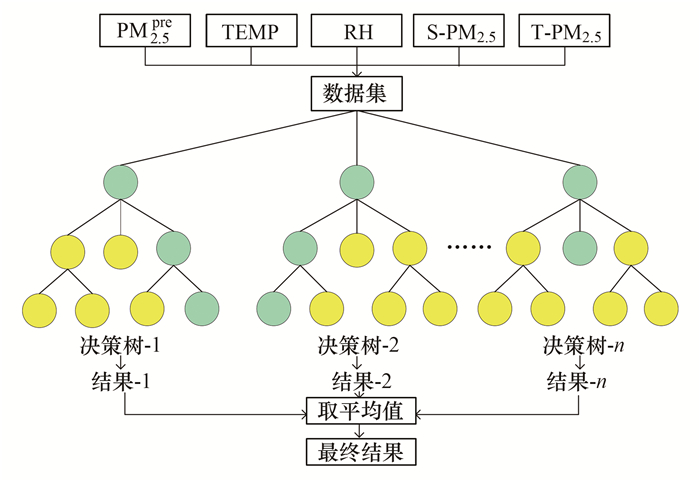
考虑到PM2.5在大气中的传输过程及其具有时间自相关的特性, PM2.5监测站点附近n个站点和同一站点前m天的PM2.5观测值对于估算PM2.5具有参考意义.用于估算PM2.5的Geoi-RF示意见图 3.输入变量为iLME模型的估算值、TEMP、RH和时空信息.其中时空信息项表示为:

(4)
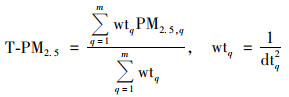
(5)
图 3 Geoi-RF示意 Fig. 3 Schematic of Geoi-RF

式中, S-PM2.5和T-PM2.5分别为空间信息项和时间信息项, m和n均为3; PM2.5, p为在空间上靠近该站点的第p个站点的PM2.5观测值; PM2.5, q为同一站点之前第q天的PM2.5观测值; wsp和wtq分别为空间上靠近该站点的第p个站点的距离加权系数和同一站点之前第q天的时间加权系数; dsp和dtq分别为空间上靠近该站点的第p个站点与该站点的空间距离和同一站点之前第q天与该站点观测时刻的时间间隔.

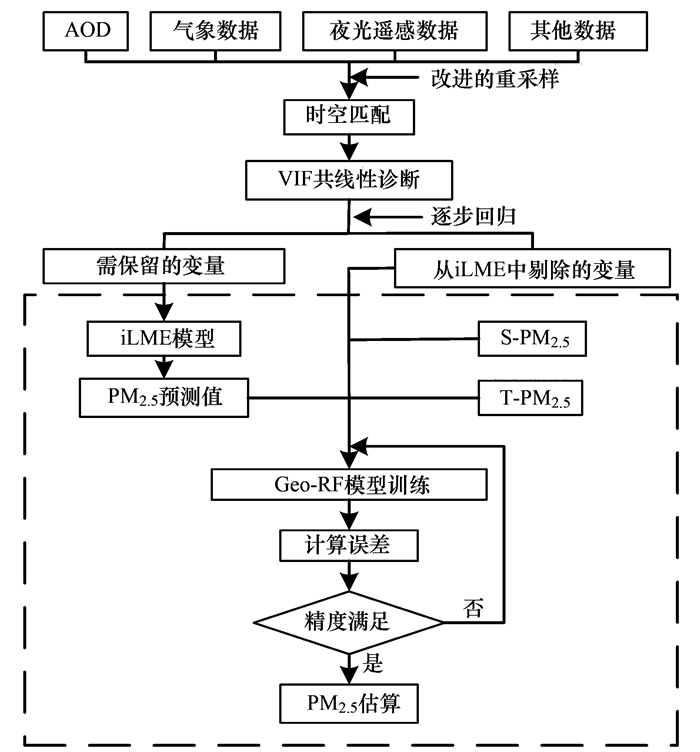
1.3.4 模型构建

iLME+Geoi-RF模型建模包括3个步骤, 即时空匹配、变量筛选和模型构建, 具体流程如图 4所示.

图 4 模型构建过程 Fig. 4 Model building process

按1.2.5节所述进行时空匹配, 计算所有变量的VIF值, 经逐步回归后得出需保留在iLME模型中的变量和需从iLME模型中剔除的变量, 需保留的变量加入iLME模型拟合, 从iLME模型中剔除的变量加入Geoi-RF进行拟合, 再利用iLME+Geoi-RF模型估算2016年四川省的PM2.5浓度空间分布.

1.3.5 模型验证

为全面客观地评价模型的估算精度, 采用决定系数(R2)、均方根误差(RMSE)和平均绝对误差(MAE)来比较地理神经网络加权回归(GNNWR)模型[29]、LME模型、iLME+BP模型、地理智能深度学习(Geoi-DBN)模型[30]、LME+Geoi-DBN模型、iLME+Geoi-DBN模型、LME+Geoi-RF模型和iLME+Geoi-RF模型的拟合效果, 并利用十折交叉验证[31]对所提出的模型进行验证, 各指标计算见式(6):

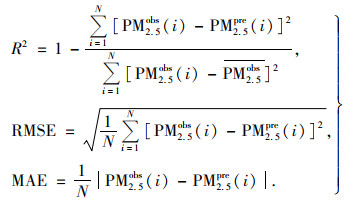
(6)

式中, N为样本总数; PM2.5obs为实测PM2.5浓度; PM2.5pre为估算PM2.5浓度; 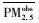为实测PM2.5浓度的平均值.

2 结果与讨论 2.1 PM2.5与估算变量的相关性分析

对16个估算变量和地面实测PM2.5进行时空匹配, 共获得10 007条有效数据, 按日进行分割求取平均值后得到3607条数据.表 3为估算变量的描述性统计, 其中2016年四川省参与建模数据的PM2.5浓度最大值为246.50 μg·m-3, 最小值为1.17 μg·m-3, 均值为24.88 μg·m-3, 年均PM2.5浓度远高于中国环境空气质量标准(GB 3095-2012)一级限值(15.00 μg·m-3)[32], 表明四川省PM2.5污染程度较高.

表 3 估算变量的描述性统计1) Table 3 Descriptive statistics of estimated variables

PM2.5与AOD、PS、TEMP、RH、BLH、CVL、u10、v10、POP、CVH、NL、RAIN和FPI呈正相关关系, 其中PM2.5与AOD密切相关, 皮尔逊相关系数高达0.65, 因为AOD为表征大气浑浊度的物理量, 其值越高表明大气污染越严重.气压、温度、相对湿度和边界层高度是影响PM2.5稀释和扩散的重要因素, 皮尔逊相关系数分别为0.58、0.55、0.54和0.35.气压升高能促使高压中心的气流下沉阻碍PM2.5扩散[33].温度的升高降低了空气流动速率, 大量污染物颗粒飘浮于空气中, 不利于大气污染物稀释和扩散[34].相对湿度的增加有助于PM2.5中的部分可溶性粒子的吸水性较强, 造成吸湿加重[35].大气中污染物的扩散和输送很大程度上依赖边界层结构, 边界层越高, 湍流作用使颗粒物和气体混合越充分.风速与PM2.5呈正相关主要因为四川省全年平均风速在0.46 m·s-1左右, 该风速对地表PM2.5的稀释和扩散能力非常弱, 却有利于大气污染物间的混合.

PM2.5与EVI、LUCC和DEM呈负相关关系, 植被是大气中PM2.5有效的清除机制之一, 大气颗粒物经植物叶片气孔进入植物体内, 参与植物代谢反应达到净化空气的目的[36].海拔高的地区受人类干扰相对较小, 人为因素产生的排放污染物也较少.

2.2 模型拟合及交叉验证

使用全数据集进行训练考察模型的拟合效果, 通过十折交叉验证考察模型的估算与泛化能力.

2.2.1 模型拟合结果

按1.2.5节所述进行时空匹配后, 按日求取平均值获得3607条数据, 将全数据集输入iLME+Geoi-RF模型进行拟合, 并与GNNWR模型、LME模型、iLME+BP模型、Geoi-DBN模型、LME+Geoi-DBN模型、iLME+Geoi-DBN模型和LME+Geoi-RF模型进行对比, 图 5和表 4为模型拟合值和地面监测站点实测值的回归分析结果.

图 5 模型拟合结果对比 Fig. 5 Comparison of model fitting results

表 4 模型拟合及交叉验证结果对比1) Table 4 Comparison of model fitting and cross-validation results

由图 5可知GNNWR模型、LME模型和Geoi-DBN模型分别能解释PM2.5浓度80%、89%和91%的变异, 在相同的条件下, 组合模型相较于单个模型拟合效果更佳, iLME+BP模型、LME+Geoi-DBN模型和LME+Geoi-RF模型分别能解释PM2.5浓度94%、92%和97%的变异, 在LME中嵌套包含地理加权系数的固定效应和随机效应后, iLME+Geoi-DBN模型和iLME+Geoi-RF模型相较于LME+Geoi-DBN模型和LME+Geoi-RF模型分别提高3%和1%的解释变异的效果.总体来看, iLME+Geoi-RF模型解释PM2.5浓度变异能力最强, 整体上具有估算PM2.5浓度的优异性.

表 4可知GNNWR模型拟合能力较差, R2、RMSR和MAE分别为0.80、10.80 μg·m-3和6.50 μg·m-3; LME模型考虑到AOD-PM2.5之间关系的时间异质性其拟合结果更理想, R2、RMSR和MAE分别为0.89、8.12 μg·m-3和4.95 μg·m-3; 考虑到PM2.5在大气中的传输过程及其具有时间自相关的特性引入时空项后, Geoi-DBN模型的拟合表现更好, R2、RMSR和MAE分别为0.91、7.42 μg·m-3和4.79 μg·m-3; 将iLME模型与BP神经网络组合后, iLME+BP模型精度明显提升, R2、RMSR和MAE分别为0.94、5.82 μg·m-3和3.91 μg·m-3; 将组合模型的BP神经网络换为Geoi-DBN后, iLME+Geoi-DBN模型效果更佳, R2、RMSR和MAE分别为0.95、5.35 μg·m-3和3.59 μg·m-3; 进一步将Geoi-RF替换Geoi-DBN后, iLME+Geoi-RF模型拟合精度进一步提高, R2、RMSR和MAE分别为0.98、3.25 μg·m-3和1.98 μg·m-3.说明iLME+Geoi-RF模型估算PM2.5浓度与地面实测PM2.5浓度符合程度更高, 误差更小, 具有更佳的拟合能力.

2.2.2 模型交叉验证结果

使用十折交叉验证用于8种模型的验证.图 6和表 4为交叉验证中模型交叉验证值和地面站点实测值的分析结果.结果表明8种模型交叉验证R2介于0.73~0.89之间, 均方根误差范围在3.25~10.80 μg·m-3, 平均绝对误差范围在1.98~6.50 μg·m-3.组合模型的交叉验证结果普遍高于单个模型, iLME+BP模型未考虑到PM2.5在大气中的传输过程及其具有时间自相关的特性, 其验证结果低于考虑时空信息的单个模型(Geoi-DBN).将LME模型与考虑时空信息的Geoi-DBN模型组合后, LME+Geoi-DBN模型精度有一定程度的提升, R2、RMSE和MAE分别为0.87、8.54 μg·m-3和5.28 μg·m-3; 在LME+Geoi-DBN基础上对LME模型进行改进后, iLME+Geoi-DBN模型交叉验证结果更佳, R2、RMSE和MAE分别为0.88、8.29 μg·m-3和5.01 μg·m-3; 使用Geoi-RF替换Geoi-DBN后, iLME+Geoi-RF模型验证精度进一步提升, R2、RMSE和MAE分别为0.89、7.95 μg·m-3和4.81 μg·m-3.综上所述, 利用iLME+Geoi-RF模型估算四川省PM2.5浓度具有很好的准确性.

图 6 模型交叉验证结果对比 Fig. 6 Comparison of model cross-validation results

2.2.3 模型稳定性分析

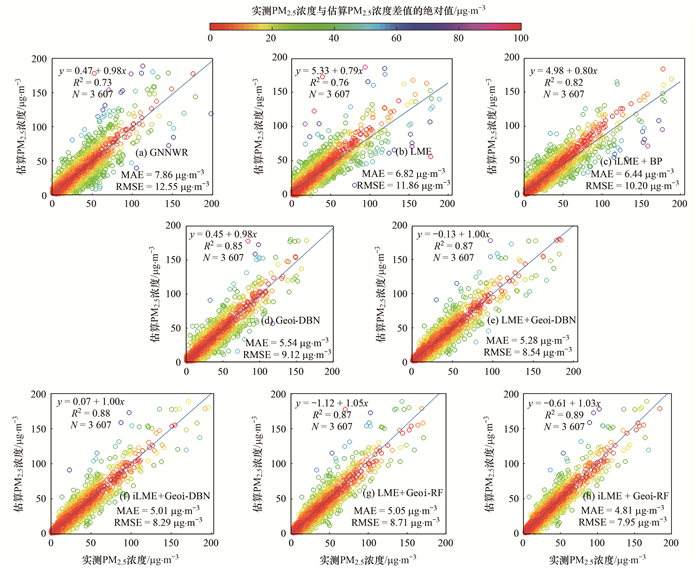
为进一步测试iLME+Geoi-RF模型的稳定性, 使用iLME+Geoi-RF模型拟合值和地面监测站点实测值的回归结果进行比较(图 7).在不同的月份, iLME+Geoi-RF模型有较高的R2(不同月份为0.94~0.98), 表明该模型获得令人满意的时间稳定性.

图 7 月尺度模型拟合结果 Fig. 7 Monthly scale model regression results

根据研究区域的实际季节划分来定义季节: 春季(3、4和5月), 夏季(6、7和8月), 秋季(9、10和11月)和冬季(12、1和2月).图 8为iLME+Geoi-RF模型在不同季节的拟合结果.该模型在春季、秋季和冬季均表现良好, R2、RMSE和MAE分别为0.98、3.89 μg·m-3和2.23 μg·m-3; 0.98、3.39 μg·m-3和2.07 μg·m-3; 0.98、3.96 μg·m-3和2.28 μg·m-3.夏季模型的拟合优度略逊一筹, R2、RMSE和MAE分别为0.96、2.84 μg·m-3和1.83 μg·m-3.但夏季RMSE和MAE均低于其他3个季节, 这可能是由于夏季实测PM2.5浓度相对其他季节较低, 导致夏季RMSE和MAE的计算结果较小.结果表明, iLME+Geoi-RF模型在各个季节均较为稳定.

图 8 季尺度模型拟合结果 Fig. 8 Seasonal scale model regression results

2.3 PM2.5时空分布

首先使用94个站点数据训练iLME+Geo-RF模型, 然后将2016年四川省各估算变量日空间分布输入训练出的iLME+Geo-RF模型得出日PM2.5浓度空间分布(其中T-PM2.5由各变量和S-PM2.5估算出的PM2.5浓度分布图获取), 最后将日PM2.5浓度空间分布叠加取平均得到四川省月均、季均的PM2.5浓度空间分布.

2.3.1 不同模型估算的PM2.5浓度空间分布

为比较不同模型在估算PM2.5空间分布上的性能差异.以2016年1月为例, 求取四川省每个PM2.5监测站点的PM2.5平均浓度, 并将iLME+BP模型和iLME+Geoi-RF模型估算的PM2.5浓度空间分布进行对比.图 9为iLME+BP模型和iLME+Geoi-RF模型估算的PM2.5浓度空间分布.

图 9 不同模型估算的PM2.5浓度空间分布 Fig. 9 Spatial distribution of PM2.5 concentration estimated by different models

由图 9可知, 不同模型估算的PM2.5浓度空间分布基本一致, 高值区主要分布在东部的成都、德阳、绵阳、广元、巴中和眉山等地区, 低值区主要分布在阿坝、甘孜和凉山等地区.但在估算PM2.5数值上, iLME+BP模型估算结果总体偏高, 尤其是在四川省东部地区, 其估算结果与地面监测站点实测结果差别较大, 而iLME+Geoi-RF模型的估算值更符合地面监测站点的监测情况, 说明iLME+Geoi-RF模型更优, 估算的PM2.5浓度空间分布更接近于真实情况.

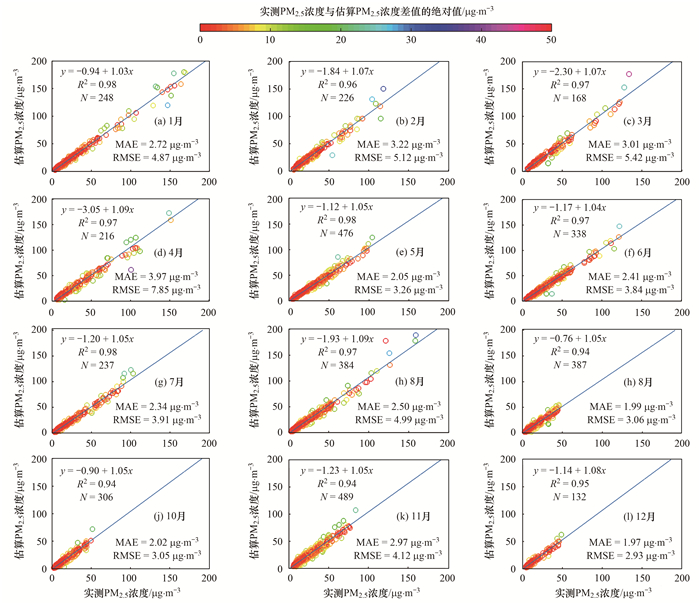
2.3.2 PM2.5月均浓度分析

基于四川省月均PM2.5浓度空间分布求取所有栅格的平均值, 即为四川省的月均PM2.5浓度, 月均PM2.5浓度随月份变化如图 10所示, 2016年四川省月均PM2.5浓度变化总体上呈“Ⅴ”型趋势, 1月PM2.5污染最严重, 平均值为63.87 μg·m-3, 其次是12、10和2月, 其平均值分别为61.61、55.15和49.48 μg·m-3, 6月PM2.5污染程度最轻微, 平均值为21.11 μg·m-3, 估算结果与PM2.5实际变化规律相符.PM2.5由1月的63.87 μg·m-3下降至6月的21.11 μg·m-3, 月均下降7.13 μg·m-3. 6~12月PM2.5浓度基本呈上升趋势, 由6月的21.11 μg·m-3上升至12月的61.61 μg·m-3, 月均上升6.75 μg·m-3, 但8月和11月的PM2.5浓度相较7月和10月有所下降, 分别下降4.01 μg·m-3和17.44 μg·m-3, 这可能是8月四川省平均气温为25.10℃, 较常年同期偏高2.00℃, 温度的升高降低了空气流动速率, 大量污染物颗粒飘浮于空气中, 不利于大气污染物稀释和扩散.在11月平均月降水量比常年偏多31%, 雨水对空气中的污染物起到清洗作用, 大气污染物随雨水流入地下.

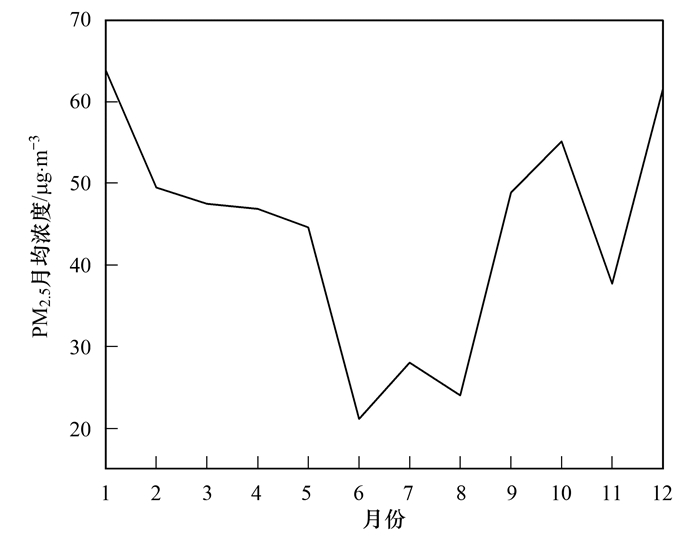
图 10 PM2.5月均浓度变化 Fig. 10 Change in monthly average concentration of PM2.5

2016年四川省月均PM2.5浓度空间分布如图 11所示, PM2.5月均浓度总体上呈现东高西低, 局部污染程度较高的特点.高污染聚集区分布于东部的成都、德阳、绵阳、广元、巴中、达州和眉山等区域, 该区域月均PM2.5浓度变化趋势与全省变化趋势一致, 总体上呈“Ⅴ”型分布, 大部分月份超过60.00 μg·m-3.该区域人口密集、经济发达, 工业生产、交通运输和能源燃烧等排放大量污染物; 加之独特的地理环境容易形成典型的地形逆温现象, 造成污染物不断累积.低污染聚集区主要集中分布在西部的甘孜、阿坝和凉山等区域, 该区域月均PM2.5浓度整体分布较均匀, 大部分月份均低于60.00 μg·m-3.该区域地形以山地和高原为主, 人口稀疏, 经济发展相对滞后, 人为排放量较少; 其次受亚热带季风气候影响, 降水量较大[37], 对PM2.5浓度起到净化和稀释作用, 因而空气质量较好.

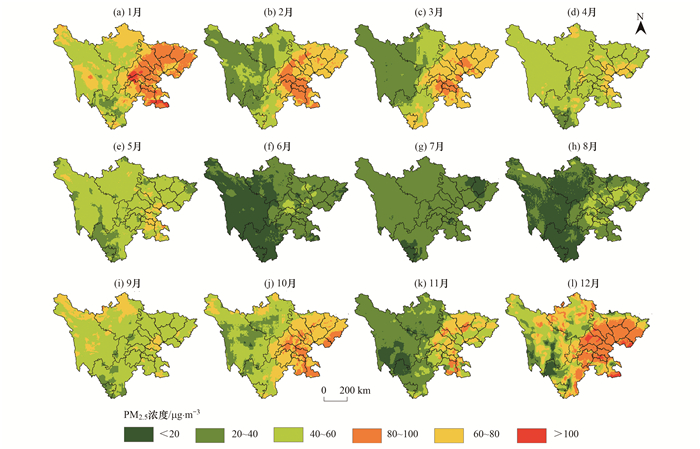
图 11 月均PM2.5空间分布 Fig. 11 Monthly average PM2.5 spatial distribution

2.3.3 PM2.5季均浓度分析

按2.2.3节所述, 以3、4和5月为春季, 6、7和8月为夏季, 9、10和11月为秋季, 1、2和12月为冬季.四川省季均PM2.5浓度存在显著的季节性差异(图 12), 一年四季的平均值依次为46.33(春季)、24.38(夏季)、47.25(秋季)和58.32 μg·m-3(冬季), 冬季PM2.5平均浓度值最高, 其次为秋季, 春季PM2.5平均浓度值与秋季相差仅0.92 μg·m-3, 夏季最低, 各季节PM2.5浓度大小依次为: 冬季>秋季>春季>夏季.

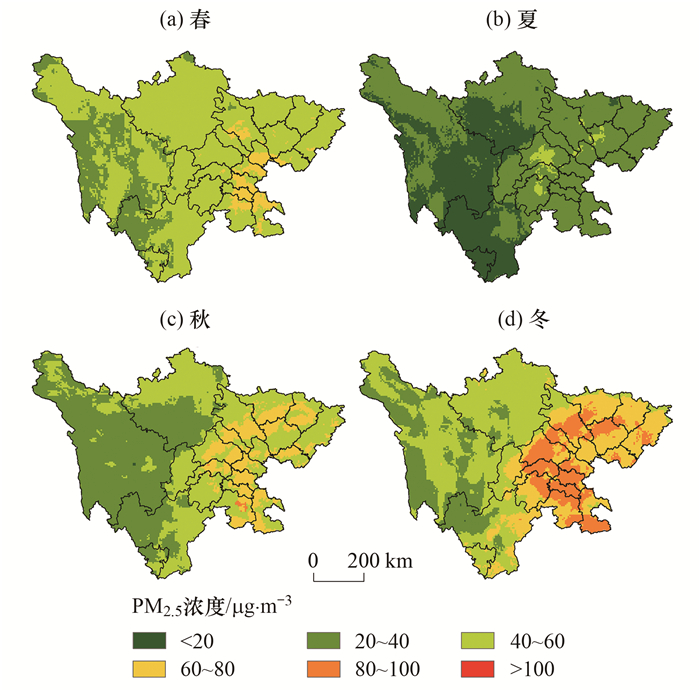
图 12 季均PM2.5空间分布 Fig. 12 Seasonal average PM2.5 spatial distribution

春季PM2.5浓度变化范围为16.96~77.96 μg·m-3, 其高值区主要分布在自贡东部、资阳东北部和遂宁东南部, 低值区主要分布在西部的阿坝、甘孜、凉山和攀枝花等地区.夏季PM2.5浓度变化范围为3.27~53.53 μg·m-3, 相比春季PM2.5浓度值大幅降低, PM2.5浓度高值区向成都中部、南充西北部、眉山东部和乐山东北部转移, 全省大部分地区PM2.5污染均有明显改善.这主要因为夏季降水量增多使空气湿度变大, 地面尘土和工业排放的污染物等不易扩散到空气中[38], 且夏季植被覆盖率最高, 植被对大气污染物质的净化较强[39].秋季PM2.5浓度变化范围为19.27~83.19 μg·m-3, PM2.5浓度上升趋势明显, 其高值区向成都平原经济区聚集, 低值区仍保持在阿坝、甘孜、凉山和攀枝花等地区.秋季干燥有风, PM2.5浓度不易聚集, 但空气中的沙尘和生物质等会引起PM2.5浓度升高[40].冬季PM2.5浓度变化范围为17.62~101.52 μg·m-3, 高值区和低值区分布与秋季类似, 但PM2.5浓度呈大幅上升趋势, 冬季寒冷干燥, 大面积取暖, 煤炭燃烧排放污染较大, 天气较冷, 出行多靠汽车, 而汽车出行次数增加也会使汽车尾气排放量增加.四川省PM2.5污染总体上呈现“东高西低”的空间分布特征, 高值区主要分布在东部的成都、德阳、绵阳、广元、巴中和眉山等地.其主要的原因是东部工业较发达、汽车尾气和人类生活排放的PM2.5浓度高, 加之成都平原经济区和川东北经济区四面环山, 不利于PM2.5的扩散.低值区主要分布在阿坝、甘孜和凉山等地区, 该地区人类活动不频繁, 污染物排放少, 且植被覆盖度较高, 对污染物的清洁作用强.

3 结论

(1) 在日尺度上分析PM2.5与所选取的各变量的相关关系, 结果表明PM2.5与AOD、PS、TEMP、RH、BLH、CVL、u10、v10、POP、CVH、NL、RAIN和FPI呈正相关关系, 而与EVI、DEM和LUCC呈负相关关系, 其中AOD、PS、TEMP、RH和BLH是影响2016年四川省PM2.5浓度的重要因素, 其相关系数分别为0.65、0.58、0.55、0.54和0.35.

(2) 与本文所对比的模型相比, 利用iLME+Geoi-RF模型估算的PM2.5浓度精度最高, 模型拟合R2、RMSR和MAE分别为0.98、3.25 μg·m-3和1.98 μg·m-3, 交叉验证R2、RMSR和MAE分别为0.89、7.95 μg·m-3和4.81 μg·m-3.充分证明该模型具有更好的模拟效果, 估算的PM2.5浓度更接近真实值, 可用于获取更高精度的四川省PM2.5时空分布特征, 为区域空气质量评估和人体暴露风险评价及环境污染治理提供更加合理的科学参考.

(3) 四川省季均PM2.5浓度存在显著季节性差异, 四季均值依次为46.33(春季)、24.38(夏季)、47.25(秋季)和58.32 μg·m-3(冬季), 各季节PM2.5浓度大小依次为: 冬季>秋季>春季>夏季.PM2.5月均浓度总体上呈先降后升的“Ⅴ”型趋势, 由1月开始下降至6月达到最小值, 月均下降7.13 μg·m-3, 6~12月基本呈上升趋势, 由6月开始上升至12月达到最大值, 月均上升6.75 μg·m-3.但8月和11月有微小起伏.从空间分布来看, 四川省PM2.5浓度总体上呈现东高西低和局部污染程度较高的特点, 高值区主要分布在城市快速发展和人口密集的东部地区, 低值区主要分布在经济发展落后和人口稀疏的西部地区.

(4) 虽然不同模型估算出PM2.5浓度整体分布基本一致, 但iLME+Geoi-RF模型估算的PM2.5浓度值能取得更理想的效果, 说明iLME+Geoi-DBN模型能更准确有效的估算本研究区污染的空间分布.

(5) 本文仍存在一些不足.①由于缺乏夜间的AOD数据, 仅根据Himawari-8卫星观测值获取24 h的PM2.5浓度是不可能的.在未来的工作中, 可通过整合地面观测值和卫星AOD数据, 以获取更高精度和更广时间覆盖范围的PM2.5浓度, 以期为区域污染治理提供数据支持.②iLME+Geoi-RF模型在月尺度和季节尺度上的结果不尽相同, 其原因可能是每个自变量在不同的月份和季节对模型的贡献不同, 对不同的变量探索、不同的加权方法及从不同的时间尺度, 探索更合理的变量组合来提升模型精度仍有待进一步地研究.

参考文献
[1] Guo Y M, Zeng H M, Zheng R S, et al. The association between lung cancer incidence and ambient air pollution in China: a spatiotemporal analysis[J]. Environmental Research, 2016, 144: 60-65. DOI:10.1016/j.envres.2015.11.004
[2] Van Donkelaar A, Martin R V, Brauer M, et al. Global estimates of fine particulate matter using a combined geophysical-statistical method with information from satellites, models, and monitors[J]. Environmental Science & Technology, 2016, 50(7): 3762-3772.
[3] 刘林钰, 张永军, 李彦胜, 等. 基于深度学习的华东地区PM2.5浓度遥感反演[J]. 环境科学, 2020, 41(4): 1513-1519.
Liu L Y, Zhang Y J, Li Y S, et al. PM2.5 inversion using remote sensing data in eastern China based on deep learning[J]. Environmental Science, 2020, 41(4): 1513-1519.
[4] Li J, Carlson B E, Lacis A A, et al. How well do satellite AOD observations represent the spatial and temporal variability of PM2.5 concentration for the United States?[J]. Atmospheric Environment, 2015, 102: 260-273. DOI:10.1016/j.atmosenv.2014.12.010
[5] Dong L C, Li S W, Yang J, et al. Investigating the performance of satellite-based models in estimating the surface PM2.5 over China[J]. Chemosphere, 2020, 256. DOI:10.1016/j.chemosphere.2020.127051
[6] Wei J, Huang W, Li Z Q, et al. Estimating 1-km-resolution PM2.5 concentrations across China using the space-time random forest approach[J]. Remote Sensing of Environment, 2019, 231. DOI:10.1016/j.rse.2019.111221
[7] Ma Z W, Liu Y, Zhao Q Y, et al. Satellite-derived high resolution PM2.5 concentrations in Yangtze River Delta Region of China using improved linear mixed effects model[J]. Atmospheric Environment, 2016, 133: 156-164. DOI:10.1016/j.atmosenv.2016.03.040
[8] Chen W Q, Ran H F, Cao X Y, et al. Estimating PM2.5 with high-resolution 1-km AOD data and an improved machine learning model over Shenzhen, China[J]. Science of the Total Environment, 2020, 746. DOI:10.1016/j.scitotenv.2020.141093
[9] Guo J P, Xia F, Zhang Y, et al. Impact of diurnal variability and meteorological factors on the PM2.5-AOD relationship: implications for PM2.5 remote sensing[J]. Environmental Pollution, 2017, 221: 94-104. DOI:10.1016/j.envpol.2016.11.043
[10] Mao F Y, Min Q L, Liu G Y, et al. Assimilating moderate resolution imaging spectroradiometer radiance with the weather research and forecasting data assimilation system[J]. Journal of Applied Remote Sensing, 2017, 11(3). DOI:10.1117/1.jrs.11.036002
[11] Xin J Y, Gong C S, Liu Z R, et al. The observation-based relationships between PM2.5 and AOD over China[J]. Journal of Geophysical Research: Atmospheres, 2016, 121(18): 10701-10716. DOI:10.1002/2015JD024655
[12] Lee H J, Liu Y, Coull B A, et al. A novel calibration approach of MODIS AOD data to predict PM2.5 concentrations[J]. Atmospheric Chemistry and Physics, 2011, 11(15): 7991-8002. DOI:10.5194/acp-11-7991-2011
[13] Ma Z W, Hu X F, Huang L, et al. Estimating ground-level PM2.5 in China using satellite remote sensing[J]. Environmental Science & Technology, 2014, 48(13): 7436-7444.
[14] Bai Y, Wu L X, Qin K, et al. A geographically and temporally weighted regression model for ground-level PM2.5 estimation from satellite-derived 500m resolution AOD[J]. Remote Sensing, 2016, 8(3). DOI:10.3390/rs8030262
[15] Zuo X, Guo H, Shi S Y, et al. Comparison of six machine learning methods for estimating PM2.5 concentration using the Himawari-8 aerosol optical depth[J]. Journal of the Indian Society of Remote Sensing, 2020, 48(9): 1277-1287. DOI:10.1007/s12524-020-01154-z
[16] Di Q, Koutrakis P, Schwartz J, et al. A hybrid prediction model for PM2.5 mass and components using a chemical transport model and land use regression[J]. Atmospheric Environment, 2016, 131: 390-399. DOI:10.1016/j.atmosenv.2016.02.002
[17] Hu X F, Belle J H, Meng X, et al. Estimating PM2.5 concentrations in the conterminous United States using the random forest approach[J]. Environmental Science & Technology, 2017, 51(12): 6936-6944.
[18] Chen J P, Yin J H, Zang L, et al. Stacking machine learning model for estimating hourly PM2.5 in China based on Himawari-8 aerosol optical depth data[J]. Science of The Total Environment, 2019, 697. DOI:10.1016/j.scitotenv.2019.134021
[19] 沈焕锋, 李同文. 大气PM2.5遥感制图研究进展[J]. 测绘学报, 2019, 48(12): 1624-1635.
Shen H F, Li T W. Progress of remote sensing mapping of atmospheric PM2.5[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(12): 1624-1635.
[20] Kikuchi M, Murakami H, Suzuki K, et al. Improved hourly estimates of aerosol optical thickness using spatiotemporal variability derived from Himawari-8 geostationary satellite[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(6): 3442-3455. DOI:10.1109/TGRS.2018.2800060
[21] Zang L, Mao F Y, Guo J P, et al. Estimating hourly PM1 concentrations from Himawari-8 aerosol optical depth in China[J]. Environmental Pollution, 2018, 241: 654-663. DOI:10.1016/j.envpol.2018.05.100
[22] Liu J J, Weng F Z, Li Z Q, et al. Satellite-based PM2.5 estimation directly from reflectance at the top of the atmosphere using a machine learning algorithm[J]. Atmospheric Environment, 2019, 208: 113-122. DOI:10.1016/j.atmosenv.2019.04.002
[23] Su T N, Li Z Q, Kahn R. Relationships between the planetary boundary layer height and surface pollutants derived from lidar observations over China: regional pattern and influencing factors[J]. Atmospheric Chemistry and Physics, 2018, 18(21): 15921-15935. DOI:10.5194/acp-18-15921-2018
[24] Xue W H, Zhang J, Zhong C, et al. Satellite-derived spatiotemporal PM2.5 concentrations and variations from 2006 to 2017 in China[J]. Science of The Total Environment, 2020, 712. DOI:10.1016/j.scitotenv.2019.134577
[25] Retalis A, Sifakis N. Urban aerosol mapping over Athens using the differential textural analysis (DTA) algorithm on MERIS-ENVISAT data[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2010, 65(1): 17-25. DOI:10.1016/j.isprsjprs.2009.08.001
[26] 周爽, 王春林, 孙睿, 等. 基于LME/BME的珠江三角洲PM2.5星地融合技术研究[J]. 中国环境科学, 2019, 39(5): 1869-1878.
Zhou S, Wang C L, Sun R, et al. Fusion of satellite data and ground observed PM2.5 in Pearl River Delta region with linear mixed effect and Bayesian maximum entropy method[J]. China Environmental Science, 2019, 39(5): 1869-1878. DOI:10.3969/j.issn.1000-6923.2019.05.010
[27] Kuznetsova A, Brockhoff P B, Christensen R H B. lmerTest package: tests in linear mixed effects models[J]. Journal of Statistical Software, 2017, 82(13): 1-26.
[28] Xiao Q Y, Chang H H, Geng G N, et al. An ensemble machine-learning model to predict historical PM2.5 concentrations in China from satellite data[J]. Environmental science & technology, 2018, 52(22): 13260-13269.
[29] Du Z H, Wang Z Y, Wu S S, et al. Geographically neural network weighted regression for the accurate estimation of spatial non-stationarity[J]. International Journal of Geographical Information Science, 2020, 34(7): 1353-1377. DOI:10.1080/13658816.2019.1707834
[30] Li T W, Shen H F, Yuan Q Q, et al. Estimating ground-level PM2.5 by fusing satellite and station observations: a geo-intelligent deep learning approach[J]. Geophysical Research Letters, 2017, 44(23): 11985-11993. DOI:10.1002/2017GL075710
[31] 郝静, 孙成, 郭兴宇, 等. 京津冀内陆平原区PM2.5浓度时空变化定量模拟[J]. 环境科学, 2018, 39(4): 1455-1465.
Hao J, Sun C, Guo X Y, et al. Simulation of the spatio-temporally resolved PM2.5 aerosol mass concentration over the inland plain of the Beijing-Tianjin-Hebei region[J]. Environmental Science, 2018, 39(4): 1455-1465.
[32] 夏晓圣, 汪军红, 宋伟东, 等. 2000~2019年中国PM2.5时空演化特征[J]. 环境科学, 2020, 41(11): 4832-4843.
Xia X S, Wang J H, Song W D, et al. Spatio-temporal evolution of PM2.5 concentration during 2000-2019 in China[J]. Environmental Science, 2020, 41(11): 4832-4843.
[33] 魏石梅, 潘竟虎, 妥文亮. 2015年中国PM2.5浓度遥感估算与时空分布特征[J]. 遥感技术与应用, 2020, 35(4): 845-854.
Wei S M, Pan J H, Tuo W L. Estimation and spatial-temporal distribution characteristics of PM2.5 concentration by remote sensing in China in 2015[J]. Remote sensing technology and application, 2020, 35(4): 845-854.
[34] 李佳旭. 成都市PM2.5浓度的影响因素分析及预测[D]. 兰州: 兰州大学, 2020.
Li J X. Research on forecast and influencing factors of PM2.5 concentration in Chengdu[D]. Lanzhou: Lanzhou University, 2020.
[35] 黄小刚, 赵景波, 辛未冬. 基于网格的长三角PM2.5分布影响因素及交互效应[J]. 环境科学, 2021, 42(7): 3107-3117.
Huang X G, Zhao J B, Xin W D. Factors and their interaction effects on the distribution of PM2.5 in the Yangtze River Delta based on grids[J]. Environmental Science, 2021, 42(7): 3107-3117.
[36] 鲁绍伟, 蒋燕, 陈波, 等. 北京城市植被区PM2.5浓度时空变化及影响因素分析[J]. 环境科学与技术, 2017, 40(1): 180-187.
Lu S W, Jiang Y, Chen B, et al. Analysis on spatial-temporal variation and influential factors of PM2.5 mass concentration in Beijing's Urban Forest[J]. Environmental Science & Technology, 2017, 40(1): 180-187.
[37] 李梦真, 张廷斌, 易桂花, 等. 四川盆地PM2.5浓度时空变化特征遥感监测与影响因子分析[J]. 环境科学, 2021, 42(7): 3136-3146.
Li M Z, Zhang T B, Yi G H, et al. Spatio-temporal variation characteristics monitored by remotely sensed technique of PM2.5 concentration and its influencing factor analysis in Sichuan Basin, China[J]. Environmental Science, 2021, 42(7): 3136-3146.
[38] 杨晓辉, 宋春杰, 范丽行, 等. 京津冀地区高分辨率PM2.5浓度时空变化模拟与分析[J]. 环境科学, 2021, 42(9): 4083-4094.
Yang X H, Song C J, Fan L X, et al. Estimating the spatio-temporal variation of PM2.5 concentrations with high resolution in the Beijing-Tianjin-Hebei region[J]. Environmental Science, 2021, 42(9): 4083-4094.
[39] 金囝囡, 杨兴川, 晏星, 等. 京津冀及周边MAIAC AOD和PM2.5质量浓度特征及相关性分析[J]. 环境科学, 2021, 42(6): 2604-2615.
Jin N N, Yang X C, Yan X, et al. MAIAC AOD and PM2.5 mass concentration characteristics and correlation analysis in Beijing-Tianjin-Hebei and surrounding areas[J]. Environmental Science, 2021, 42(6): 2604-2615.
[40] 夏晓圣. 中国PM2.5时空变化特征及其影响因素研究[D]. 芜湖: 安徽师范大学, 2020.
Xia X S. Spatio-temporal evolution and influencing factors of PM2.5 concentration in China[D]. Wuhu: Anhui Normal University, 2020.