2. 兰州交通大学土木工程学院, 兰州 730070
2. College of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China
NO2作为大气中重要的痕量气体之一, 极大地影响着生态环境和人们的身体健康[1, 2]. 近年来, 随着中国经济的飞速发展, 工业活动与城市化带来的能源消耗和污染物排放急剧增加, 使中国成为全球主要排放NO2的地区之一[3], 尤其是中国京津冀、长江三角洲等地区. 中国已在全国范围内建立大量的环境监测站来监测NO2和其它大气污染物浓度, 然而, 由于NO2浓度在空间上的动态变化以及环境监测站的空间分布相对有限, 对于大尺度空间连续的地面NO2浓度分布信息存在较大的不确定性. 近年来, 卫星遥感观测为获取连续空间分布的地面NO2浓度分布提供了可靠的数据支持[4, 5], 如全球臭氧检测仪[6, 7](GOME)、高空间分辨率臭氧层观测仪[8](OMI)和对流层监测仪(TROPOMI)[9, 10]等, 这些传感器都能够获取大气NO2光谱数据, 且对流层NO2浓度与地面NO2浓度分布存在高度相关性, 因此可以利用卫星遥感数据并使用反演算法来估算模拟地面NO2浓度.
目前, 基于卫星遥感监测的近地面NO2高分辨率空间分布的估算主要采用物理模型、统计模型和机器学习算法这3种方法. 物理模型利用大气物理化学传输模式结合卫星观测的NO2柱浓度来估算近地面的NO2浓度[11, 12]. 这种算法在一定程度上填补了地面监测的局限性, 然而, 该方法的模型结构较为复杂, 估算精度和时间分辨率容易受到污染物排放清单以及大气物理化学反应过程关键参数设置等因素的影响[13], 在实际的大气污染物估算中仍受较多限制. 统计模型是一种利用对流层与地面NO2之间的统计相关性, 并结合相关的辅助因子进行估算的方法. 由于统计模型具有数据来源广、建模方法灵活、通用性广等特点, 已经成为估算地面NO2浓度的常用手段[14, 15], 如土地利用回归(LUR)[16]和地理加权回归(GWR)[17, 18], 但影响近地面NO2浓度因素众多且变化大, 导致NO2成因机制复杂. 因此传统的经验统计模型很难完全解释NO2及其影响因素之间的非线性和高阶相互作用. 机器学习方法具有完整的模型结构和很强的拟合能力, 能够更好地处理NO2与其影响因素之间的非线性关系, 并且模型训练速度快, 处理数据集效率高. 游介文等[19]利用随机森林模拟了中国近地面NO2浓度, 对比分析了随机森林和传统土地利用回归模型对于近地面NO2浓度的模拟, 结果表明随机森林月均模型拟合度R2为0.85, 显著高于LUR模型. Chi等[20]利用梯度提升决策树模拟了中国近地面日NO2浓度, 日均模型拟合度R2为0.73.
现阶段, 采用传统机器学习模型进行NO2浓度模拟较为普遍, 现有的传统机器学习算法种类繁多, 模拟精度较高, 然而每种机器学习所适宜解决的问题各不相同, 没有一种机器学习算法能在所有数据集上表现最佳, 且大部分机器学习算法的性能很大程度上依赖于超参数的优化, 即使花费大量时间和精力进行机器学习建模, 仍然很难达到更高的精度水平. 因此, 本文引入自动机器学习(automated machine learning, AutoML)[21]解决上述传统机器学习中存在的问题, 自动机器学习不仅能够满足不同数据集对不同机器学习流程的需求, 支持广泛的机器学习算法, 还能自动化地进行算法选择、特征生成、超参数调整、迭代建模以及模型评估. AutoML不仅可以自动选择超参数, 还能自动选择最佳模型, 使其成为一个自动化工具, 帮助优化机器学习建模过程. 本文以中国长三角为研究区, 采用自动机器学习方法结合TROPOMI NO2柱浓度、人口、高程和气象数据, 来获得长三角地区2020年3月至2021年2月连续空间分布的日NO2污染数据, 以期为长三角地区的大气污染防治提供一定的数据支撑.
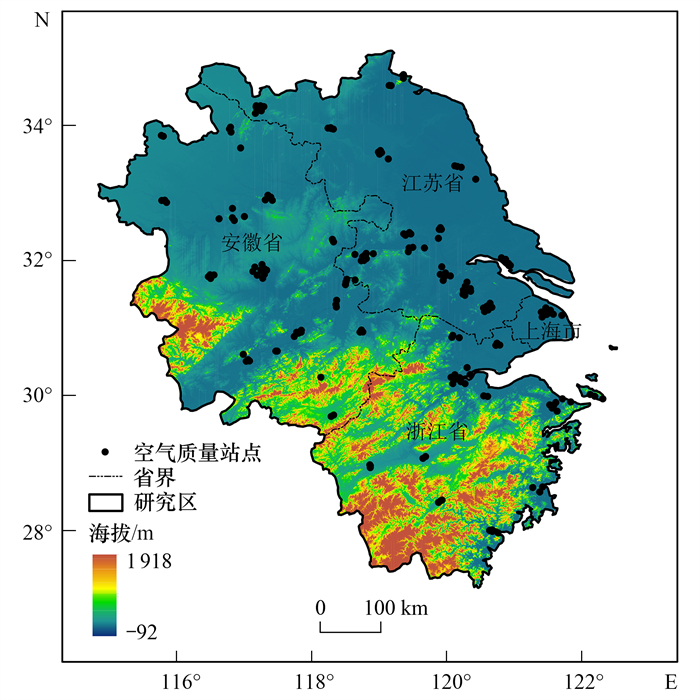
1 材料与方法 1.1 研究区与数据来源本文研究区为中国长江三角洲地区, 包括上海市、江苏省、安徽省和浙江省. 研究区如图 1所示. 本文使用的数据主要包括:2020年3月至2021年2月地面NO2浓度监测数据、TROPOMI对流层NO2柱浓度数据、ERA5气象再分析数据、高程和人口密度数据. 地面NO2监测数据来源于中国环境监测总站(http://www.cnemc.cn/)发布的全国空气质量监测站点逐小时数据. 对流层NO2柱浓度数据来源于欧洲航天局发布的基于TROPOMI传感器OFFLINE版本的对流层NO2柱浓度二级产品(https://s5phub.copernicus.eu/dhus/#/home). 气象数据来源于欧洲中期天气预报中心的ERA5陆地逐小时数据集, 下载的气象数据包括:2 m地表温度(T2M)、2 m露点温度(D2M)、10 m东风速(U10)、10 m北风速(V10)、边界层高度(BLH)、地面太阳净辐射(SSR)、地面太阳辐射向下(SSRD)、地面净热辐射(STR)、地面热辐射向下(STRD)、总蒸发量(ET)、地表压强(SP)、垂直风速(VV)和相对湿度(RH). 地形高程(DEM)数据来源于中国科学院资源环境科学与数据中心(https://www.resdc.cn/). 人口密度数据(MPD)来源于WorldPop(https://www.worldpop.org/). 本文将所有数据空间分辨率统一到0.03°, 并剔除异常值和空缺值.
|
图 1 研究区示意 Fig. 1 Location of study area |
自动机器学习(AutoML)是一种通过将机器学习任务的设计、优化和部署过程自动化的技术[22]. 自动机器学习引入了元学习和集成学习这两个额外的关键组件来增强性能. 元学习(meta learning)[23]是一种机器学习范式, 它的目标是让机器学习算法自动学习如何在不同任务之间泛化. 在AutoML中用于初始化贝叶斯优化流程[24], 通过基于元学习选择一组初始配置, 然后用于贝叶斯优化过程, 从而节省了时间并提高了效率. 这意味着AutoML不仅能够自动化地搜索最佳模型配置, 还能够更智能地为贝叶斯优化提供初始值, 使整个优化过程更加迅速和精确. 元学习可以用于自动选择适合特定任务的机器学习算法、模型架构或超参数设置, 可以通过观察和学习来自多个任务的数据和模型性能, 以提高在新任务上的表现. 其次, AutoML还引入了自动集成(automated ensemble)的功能. 这意味着它能够自动创建性能最佳的集成模型, 从而进一步提高了模型的预测性能. 通过将多个不同的模型组合在一起, AutoML可以降低单个模型的偏差和方差, 提供更稳健和准确的预测. 集成学习(ensemble learning)[25]是一种通过组合多个基础学习算法来构建更强大和稳健的预测模型的机器学习技术. 其核心思想是将多个弱学习器合并在一起, 形成一个更具有泛化能力和准确性的强学习器. Stacking集成算法[26]结合了不同种类的算法作为基学习器, 并将简单的回归算法作为强学习器. 在Stacking中, 各个基学习器的训练结果作为强学习器的输入, 而强学习器的输出则为最终的预测结果. 通过这种方式, Stacking能够将不同学习器的优势进行有效整合, 形成更具有表现力的强学习器, 从而提升预测性能.
本文利用Pycaret自动化机器学习接口来创建最佳的NO2模拟模型, Pycaret是一个自动机器学习工具, 其中含有3类主流机器学习模型:树状模型[27]、梯度提升模型[28]和广义线性模型[29], 共内置有25种算法. 本文基于自动机器学习获取了表现性能较好的前5种机器学习:随机森林(RF)、极端随机树(ET)、极端梯度提升树(XGBoost)、轻量级提升树(LightGBM)和Catboost, 并利用Stacking集成算法融合5种机器学习, 这5种机器学习方法均基于回归树构建, 能够很好地处理NO2与其它影响因子之间的非线性关系, RF[30]和ET[31]都是基于决策树的树状模型, 可以随机选择预测样本, 提高了模型的泛化程度[32]. 而XGBoost[33]、LightGBM[34]和CatBoost[35]是3个基于梯度提升决策树代表性的算法实现, 通过迭代地训练一系列弱学习器, 并将它们组合成一个强学习器, 以获得更准确和稳定的预测结果.
1.2.2 模型评估指标本文使用的评估机器学习模型的3个性能指标为:相关系数(R2)、均方根误差(RMSE)和平均绝对误差(MAE). 各指标计算公式如下:
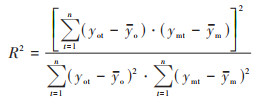
|
(1) |
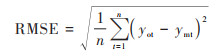
|
(2) |
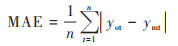
|
(3) |
式中, n为有效站点的数量;ymt为NO2的预测值;yot为NO2的实测值;ym和yo分别为NO2预测值与实测值的平均值.
2 结果与讨论 2.1 变量选取与相关性分析本文选取了18个对近地面NO2影响比较大的变量(表 1), 为了避免选择的变量之间存在冗余, 对选取的变量进行方差膨胀系数计算, 2 m地表温度、2 m露点温度、相对湿度、地面热辐射向下和地面净热辐射的VIF均大于10, 证明这些变量之间存在着较高的多重共线性, 本文依次剔除2 m地表温度、地面热辐射向下和地面净热辐射这3个变量后, 再次计算方差膨胀系数后VIF均小于10, 符合要求.
|
|
表 1 方差膨胀系数对比1) Table 1 Comparison of variance expansion factors |
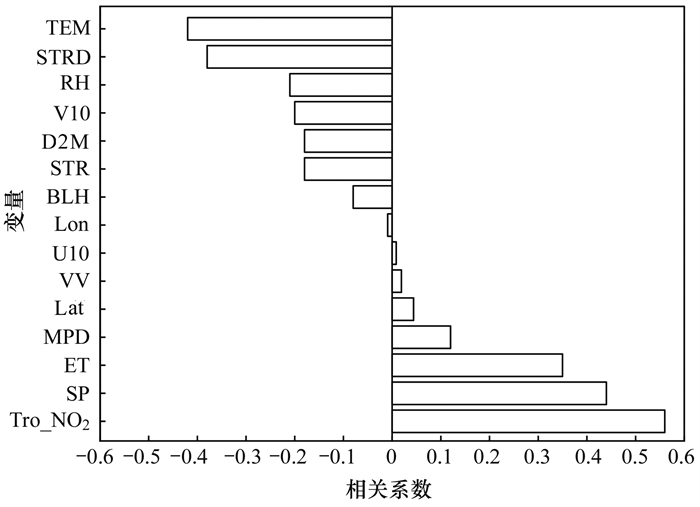
本文对这15个变量与NO2实测数据进一步进行相关性分析, 如图 2所示. 从近地面NO2浓度与各特征变量之间的相关性结果来看, 具有较高相关性的特征变量首先是Tro_NO2, 其次大部分都是气象要素数据. 近地面NO2浓度与Tro_NO2、SP、ET和MPD呈明显正相关;与D2M、STR、RH、V10、DEM、STRD和BLH呈明显负相关;与Lon、U10和VV相关性较弱. 因此逐渐剔除相关性较弱的变量, 直到确定模型的最优变量组合. 经过变量筛选与模型训练, 当仅剔除VV这一变量时, 模型的精度最高, 误差最小. 故剔除VV这一变量, 最终选择剩余14个对近地面NO2浓度和模型性能影响较大的因素(Lat、Lon、Tro_NO2、D2M、U10、V10、BLH、RH、STRD、STR、SP、ET、DEM和MPD)作为模型的输入变量.
|
图 2 NO2与其影响因素的相关性 Fig. 2 Correlation between NO2 andits influencing factors |
本文最终选择14个影响NO2浓度的变量结合自动机器学习法, 采用十折交叉验证的方式对估算结果进行验证, 训练集占样本总数的80%, 测试集占样本总数的20%. 获取了精度较高的前5种机器学习法ET、RF、Catboost、XGBoost和LightGBM, 利用Stacking集成模型将这5种方法融合, 并与单一的这5种机器学习进行比较, Stacking集成模型和5种单一的机器学习计算结果如表 2所示, R2介于0.683到0.825之间, 均方误差介于6.932 μg·m-3到9.463 μg·m-3之间, 相对误差介于5.164 μg·m-3到7.221 μg·m-3之间. 6种算法建立的模型在训练集和测试集上性能由好到差依次为Stacking集成模型、ET、RF、Catboost、XGBoost和LightGBM. 从模拟精度和误差结果来看, 5种单一机器学习算法中, ET表现结果最好, LightGBM表现结果最差. Stacking集成模型的R2均大于0.82, 均方误差小于7.1 μg·m-3, 相对误差小于5.2 μg·m-3, 集成模型修正了不同机器学习算法的预测结果, 性能均优于任何一种机器学习算法.
|
|
表 2 模型精度对比 Table 2 Model accuracy comparison |
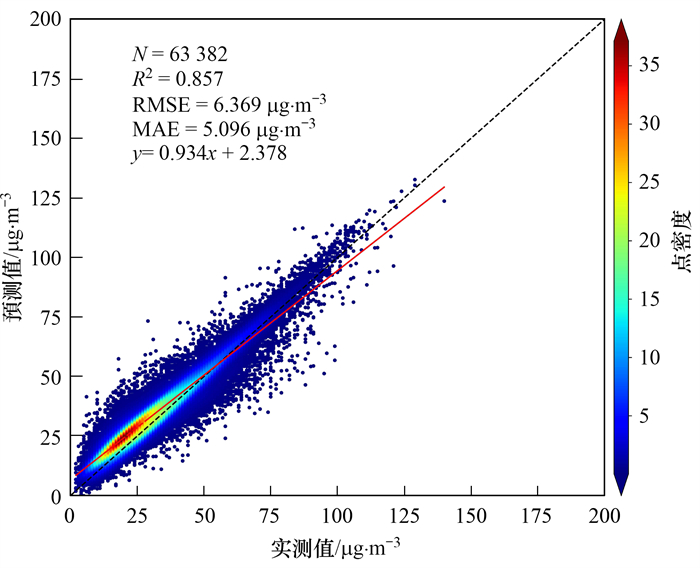
因此可选择Stacking集成模型对长三角地区每日NO2浓度进行模拟研究. 为了对比该集成模型相比实际NO2浓度的模拟效果, 本文将Stacking集成模型计算的研究区的日NO2估算浓度值和实际浓度值进行比较, 研究区日NO2估算浓度值的整体精度结果如图 3所示, 其中黑色虚线为1∶1的直线, 红色实线为精度拟合直线, 散点密度代表样本点出现的次数. 利用所有站点日NO2浓度得到有效样本数为63 382条, R2为0.857, RMSE为6.369 μg·m-3, MAE为5.096 μg·m-3, Stacking集成模型的预测精度和稳定性均处于较高水平.
|
图 3 日NO2估算值精度验证密度散点图 Fig. 3 Scatterplot of daily NO2 estimation accuracy verification density |
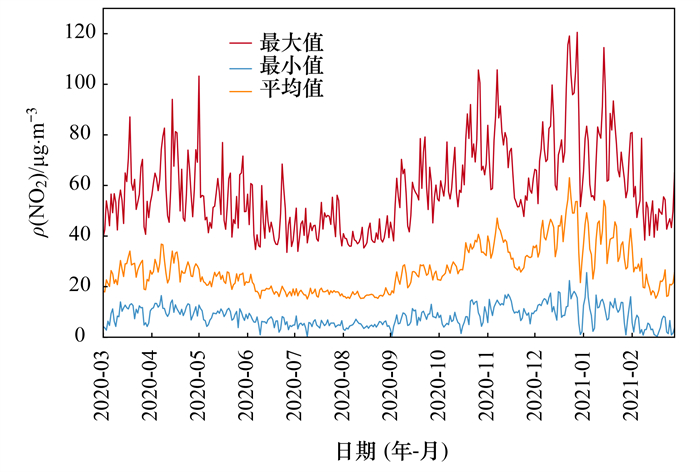
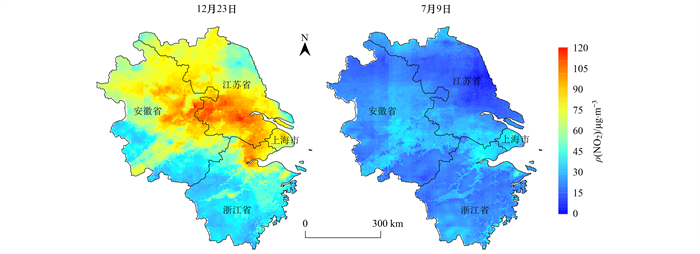
本文利用自动机器学习的Stacking集成模型融合了5种算法模拟得到了长三角地区2020年3月至2021年2月每日的近地面NO2浓度, 日尺度的变化序列如图 4所示, 包括近地面NO2浓度最大值、最小值和平均值. 可以看出NO2浓度在全年呈波浪形曲线变化, 全年近地面ρ(NO2)的最大值区间为33.5~120.5 μg·m-3, 最小值区间为0.1~22.5 μg·m-3, 平均值区间为13.6~63.0 μg·m-3. 国家颁布的GB 3095-2012中, 一、二级标准的日NO2浓度限值均为80 μg·m-3, 研究区日NO2浓度最大值高于标准限值的天数为43 d, 占比为11.8%, 低于标准限值的天数为322 d, 占比为88.2%;日NO2平均浓度全年均达到标准限值. 研究区日NO2浓度平均值的最大及最小空间分布如图 5所示. 日均NO2浓度最大的是12月23号, ρ(NO2)平均值为63.08 μg·m-3, 研究区ρ(NO2)最大值为119.12 μg·m-3, 最小值为22.41 μg·m-3;其中NO2浓度最高的地区集中在江苏省中南部、安徽省中东部和江苏省北部, 以合肥市、南京市、杭州市和上海市等城市为中心的城市群污染最为严重, 气温下降、城市机动车以及工厂排放等密集性人为活动是NO2浓度升高的主要原因. 日均NO2浓度最小的是7月9日, ρ(NO2)平均值为15.09 μg·m-3, 研究区ρ(NO2)最大值为37.3 μg·m-3, 最小值为0.15 μg·m-3.
|
图 4 近地面日NO2浓度变化 Fig. 4 Daily NO2 concentration changes near the surface |
|
图 5 日NO2浓度平均值的最大值和最小值空间分布 Fig. 5 Spatial distribution of maximum and minimum daily average NO2 concentrations |
月尺度变化趋势和日尺度整体变化趋势基本一致, 12月近地面NO2浓度平均值达到了最大, ρ(NO2)平均值为42.66 μg·m-3, 8月最小, ρ(NO2)平均值为16.54 μg·m-3. 3月NO2浓度上升, 4月达到高值后开始下降, 这是因为随着空气湿度的增加和气温的升高, 近地面NO2较快地被光化学反应转化, 从而降低了NO2浓度, 8月达到最低值, 9月NO2浓度开始上升, 随着天气变冷, 温度下降导致大气扩散条件减弱, 不利于NO2的扩散, 12月和次年1月NO2浓度进入峰值阶段, ρ(NO2)平均值达到42.66 μg·m-3和38.02 μg·m-3, 达到峰值后, 次年1~2月NO2浓度开始下降.
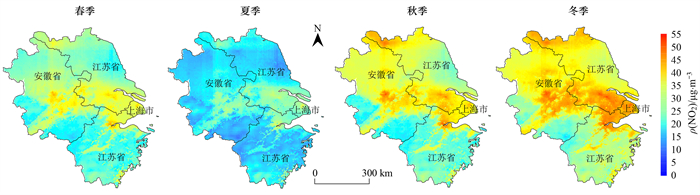
为便于描述长三角地区季节变化, 本文定义春季为2020年3月至2020年5月, 夏季为2020年6月至2020年8月, 秋季为2020年9月至2020年11月, 冬季为2020年12月至2021年2月. 长三角地区全年不同季节的NO2浓度结果如图 6所示, 全年NO2浓度时间变化特征明显. 不同季节NO2浓度平均值由高到低依次是冬季、秋季、春季和夏季, 这与何月[36]对该地区的研究结果一致, 春季和秋季NO2浓度较为相近, 浓度平均值分别为25.45 μg·m-3和29.72 μg·m-3, 夏季NO2浓度下降到研究时段内最低的水平, 浓度平均值为17.63 μg·m-3, 夏季由于气温上升紫外辐射增强以及降水量的增加, 导致大气光化学反应作用强, 氮氧化物被分解, 使得NO2浓度在整个夏季处于一个较低的水平. 冬季气温低降水偏少, 导致大气扩散能力减弱, NO2浓度进一步上升处于较高水平, 浓度平均值达34.31 μg·m-3. 空间上, 长三角地区地面NO2浓度分布整体呈现北高南低, 东高西低的趋势, 高值主要分布在上海市、江苏省南部、浙江省北部和安徽省中东部地区. 不同地区由于经济条件、资源配置和产业结构与分布等多方面的差异, 都直接影响了NO2的排放. 同时, 自然条件因素, 如城市的地貌、气候特征和地表覆盖等自然条件进一步影响了NO2的扩散和聚集. 在空间分布格局上, 长三角地区各季节近地面NO2的高浓度区域明显呈现出以太湖为中心, 口朝西南的U字形态. 以上高浓度区域对应着上海市、杭州市、南京市、苏州市和无锡市等城市群, 以及安徽省沿河流地带的城市, 如铜陵市和芜湖市等地区, 以上城市以工业化工厂分布为主. 2020年3月至2021年2月整年ρ(NO2)平均值为22.78 μg·m-3, 比国家颁布的GB 3095-2012中一级标准的年ρ(NO2)限值(40 μg·m-3)低42.5%. 结合前文分析, 可以发现近地面NO2的长期变化主要受地理环境因素和人为排放因素影响, 而气象因素则影响近地面NO2 的季节性变化和短期变化. 在2020年3月至2021年2月期间, COVID-19疫情防控措施明显减少了人为排放活动, 同时大气污染状况发生明显改变[37, 38]. 在长三角地区, NO2排放主要来自火电厂和交通排放, 由于防控措施导致机动车辆活动急剧减少, 这更加显著地降低了NO2浓度, 使得全年近地面NO2浓度处于较低水平.
|
图 6 各季节NO2浓度平均值空间分布 Fig. 6 Spatial distribution of average concentration of NO2 in different seasons |
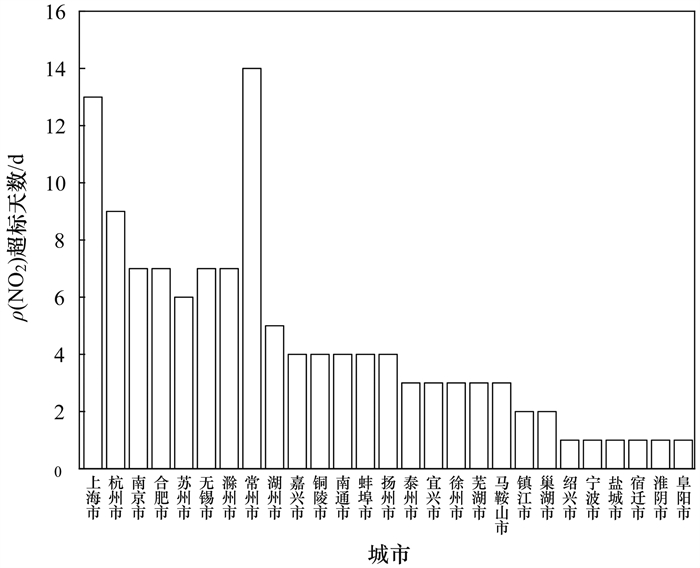
统计长三角地区2020年3月1日至2021年2月28日城市NO2近地面日均浓度, 如果城市近地面ρ(NO2)大于80 μg·m-3, 就被认为是超标, 城市近地面NO2浓度超标天数如图 7所示. 长三角地区超过国家标准日限制的城市共27个城市, 常州市是NO2污染最严重的城市, NO2浓度超标14 d, 其次是上海市, 超标13 d, 杭州市、南京市、合肥市、滁州市、苏州市和无锡市超标5 d以上, 其余城市超标5 d以下, COVID-19疫情防控措施明显减少了人为排放活动, 全年超标天数相比往年显著减少[39]. 值得注意的是, 上海市、常州市、南京市、杭州市、无锡市和苏州市等大型城市无论是近地面NO2浓度还是超标天数均明显高于其他城市, NO2高浓度值与工业区的位置分布基本一致, 特别是上海市、常州市、南通市和南京市等地区. 从铜陵市至马鞍山市地带NO2浓度较高是由于该地区分布了很多工业排放源(如化工厂和钢厂等), 另一方面还与该地区沿着河流和地形低洼的封闭型地形不易于污染物扩散有关.
|
图 7 城市近地面NO2浓度超标天数 Fig. 7 Days with NO2 concentrations above the limit near the urban ground |
(1)利用自动机器学习获得RF、ET、Catboost、XGBoost和LightGBM这5种单一机器学习与Stacking集成模型之间的精度, 结果表明5种单一机器学习方法中, ET表现结果最好, LightGBM表现结果最差, 而Stacking集成模型性均能优于任何一种机器学习算法.
(2)选择Stacking集成模型对长三角地区每日NO2浓度进行模拟研究, Stacking集成模型的最终估算结果与地面站点监测结果吻合度较高, Stacking集成模型修正了不同机器学习算法的预测结果, 集成模型的R2、RMSE和MAE值分别为0.822, 7.078 μg·m-3和5.270 μg·m-3, 表明该集成模型模拟长三角地区日NO2浓度结果具有较高的可靠性.
(3)2020年3月至2021年2月长三角地区近地面NO2浓度呈全年空间分布特征相似, 时间变化特征明显的时空格局. 近地面NO2浓度在全年呈波浪形曲线变化, 全年近地面ρ(NO2)的最大值区间为33.5~120.5 μg·m-3, 最小值区间为0.1~22.5 μg·m-3, 平均值区间为13.6~63.0 μg·m-3. 近地面NO2空间分布基本呈现以三省交汇处为中心, 口朝西南方向的U字形格局, NO2高浓度值主要分布在安徽省中东部、江苏省南部、浙江省北部和上海市地区, 其中以上海市、杭州市、南京市和合肥市为中心形成的城市群污染尤为显著. 长三角地区超过国家标准日限制的城市共27个城市, 常州市是NO2污染最严重的城市, NO2浓度超标14 d, 其次是上海市, 超标13 d. NO2浓度季节分布特点为:冬季 > 秋季 > 春季 > 夏季, 其中夏季7月9日NO2污染最轻, 冬季12月23日NO2污染最严重.
| [1] | Solomon S, Portmann R W, Sanders R W, et al. On the role of nitrogen dioxide in the absorption of solar radiation[J]. Journal of Geophysical Research: Atmospheres, 1999, 104(D10): 12047-12058. DOI:10.1029/1999JD900035 |
| [2] |
何淼, 石昌浩, 佘铉捷, 等. 2019冠状病毒病暴发初期时空特征及污染物评估[J]. 中山大学学报(自然科学版)(中英文), 2022, 61(4): 11-21. He M, Shi C H, She X J, et al. Spatial-temporal characteristics and pollutant assessment in the early stage of COVID-19 outbreak in China[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2022, 61(4): 11-21. |
| [3] | Georgoulias A K, van der A R J, Stammes P, et al. Trends and trend reversal detection in 2 decades of tropospheric NO2 satellite observations[J]. Atmospheric Chemistry and Physics, 2019, 19(9): 6269-6294. DOI:10.5194/acp-19-6269-2019 |
| [4] | Cui Y Z, Wang L, Jiang L, et al. Dynamic spatial analysis of NO2 pollution over China: satellite observations and spatial convergence models[J]. Atmospheric Pollution Research, 2021, 12(3): 89-99. DOI:10.1016/j.apr.2021.02.003 |
| [5] |
高晋徽, 朱彬, 王言哲, 等. 2005~2013年中国地区对流层二氧化氮分布及变化趋势[J]. 中国环境科学, 2015, 35(8): 2307-2318. Gao J H, Zhu B, Wang Y Z, et al. Distribution and long-term variation of tropospheric NO2 over China during 2005 to 2013[J]. China Environmental Science, 2015, 35(8): 2307-2318. DOI:10.3969/j.issn.1000-6923.2015.08.008 |
| [6] | Wagner T, Wittrock F, Richter A, et al. Continuous monitoring of the high and persistent chlorine activation during the Arctic winter 1999/2000 by the GOME instrument on ERS-2[J]. Journal of Geophysical Research: Atmospheres, 2002, 107(D20). DOI:10.1029/2001JD000466 |
| [7] | Richter A, Burrows J P. Tropospheric NO2 from GOME measurements[J]. Advances in Space Research, 2002, 29(11): 1673-1683. DOI:10.1016/S0273-1177(02)00100-X |
| [8] | Bucsela E J, Celarier E A, Wenig M O, et al. Algorithm for NO2 vertical column retrieval from the ozone monitoring instrument[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(5): 1245-1258. DOI:10.1109/TGRS.2005.863715 |
| [9] | van Geffen J, Boersma K F, Eskes H, et al. S5P TROPOMI NO2 slant column retrieval: method, stability, uncertainties and comparisons with OMI[J]. Atmospheric Measurement Techniques, 2020, 13(3): 1315-1335. DOI:10.5194/amt-13-1315-2020 |
| [10] | Sekiya T, Miyazaki K, Eskes H, et al. A comparison of the impact of TROPOMI and OMI tropospheric NO2 on global chemical data assimilation[J]. Atmospheric Measurement Techniques, 2022, 15(6): 1703-1728. DOI:10.5194/amt-15-1703-2022 |
| [11] |
陈良富, 顾坚斌, 王甜甜, 等. 近地面NO2浓度卫星遥感估算问题[J]. 环境监控与预警, 2016, 8(3): 1-5. Chen L F, Gu J B, Wang T T, et al. Scientific problems for ground NO2 concentrations estimation using DOAS method from satellite observation[J]. Environmental Monitoring and Forewarning, 2016, 8(3): 1-5. DOI:10.3969/j.issn.1674-6732.2016.03.001 |
| [12] | Marais E A, Roberts J F, Ryan R G, et al. New observations of NO2 in the upper troposphere from TROPOMI[J]. Atmospheric Measurement Techniques, 2021, 14(3): 2389-2408. DOI:10.5194/amt-14-2389-2021 |
| [13] | Liu Y, Park R J, Jacob D J, et al. Mapping annual mean ground-level PM2.5 concentrations using multiangle imaging spectroradiometer aerosol optical thickness over the contiguous United States[J]. Journal of Geophysical Research: Atmospheres, 2004, 109(D22). DOI:10.1029/2004JD005025 |
| [14] | Knibbs L D, Hewson M G, Bechle M J, et al. A national satellite-based land-use regression model for air pollution exposure assessment in Australia[J]. Environmental Research, 2014, 135: 204-211. DOI:10.1016/j.envres.2014.09.011 |
| [15] | Qin K, Rao L L, Xu J, et al. Estimating ground level NO2 concentrations over Central-Eastern China using a satellite-based geographically and temporally weighted regression model[J]. Remote Sensing, 2017, 9(9). DOI:10.3390/rs9090950 |
| [16] | Dong J, Ma R, Cai P L, et al. Effect of sample number and location on accuracy of land use regression model in NO2 prediction[J]. Atmospheric Environment, 2021, 246: 118057. DOI:10.1016/j.atmosenv.2020.118057 |
| [17] |
王媛媛, 韩骥, 过仲阳. 城市化对中国地级市NO2污染的影响研究[J]. 环境污染与防治, 2020, 42(10): 1200-1204, 1210. Wang Y Y, Han J, Guo Z Y. Influence of urbanization on NO2 pollution in prefecture-level city in China[J]. Environmental Pollution and Control, 2020, 42(10): 1200-1204, 1210. |
| [18] |
赵晶娅, 徐铖铖, 刘攀. 基于地理加权回归的NO2排放预测模型[J]. 安全与环境学报, 2019, 19(3): 964-970. Zhao J Y, Xu C C, Liu P. NO2 emission prediction model via geographically weighted regression method[J]. Journal of Safety and Environment, 2019, 19(3): 964-970. |
| [19] |
游介文, 邹滨, 赵秀阁, 等. 基于随机森林模型的中国近地面NO2浓度估算[J]. 中国环境科学, 2019, 39(3): 969-979. You J W, Zou B, Zhao X G, et al. Estimating ground-level NO2 concentrations across mainland China using random forests regression modeling[J]. China Environmental Science, 2019, 39(3): 969-979. DOI:10.3969/j.issn.1000-6923.2019.03.009 |
| [20] | Chi Y L, Fan M, Zhao C F, et al. Machine learning-based estimation of ground-level NO2 concentrations over China[J]. Science of the Total Environment, 2022, 807. DOI:10.1016/j.scitotenv.2021.150721 |
| [21] | Gianinetto M, Aiello M, Vezzoli R, et al. Future scenarios of soil erosion in the alps under climate change and land cover transformations simulated with automatic machine learning[J]. Climate, 2020, 8(2). DOI:10.3390/cli8020028 |
| [22] | Benghzial K, Raki H, Bamansour S, et al. GHG global emission prediction of synthetic N fertilizers using expectile regression techniques[J]. Atmosphere, 2023, 14(2). DOI:10.3390/atmos14020283 |
| [23] | Reif M, Shafait F, Dengel A. Meta-learning for evolutionary parameter optimization of classifiers[J]. Machine Learning, 2012, 87(3): 357-380. DOI:10.1007/s10994-012-5286-7 |
| [24] | Brochu E, Cora V M, De Freitas N. A tutorial on Bayesian optimization of expensive cost functions, with application to active user modeling and hierarchical reinforcement learning[J]. arXiv: 1012.2599, 2010. |
| [25] | Lacoste A, Larochelle H, Marchand M, et al. Agnostic Bayesian learning of ensembles[A]. In: Proceedings of the 31st International Conference on Machine Learning[C]. Beijing: JMLR. org, 2014. 611-619. |
| [26] | Agarwal S, Chowdary C R. A-stacking and A-bagging: adaptive versions of ensemble learning algorithms for spoof fingerprint detection[J]. Expert Systems with Applications, 2020, 146. DOI:10.1016/j.eswa.2019.113160 |
| [27] | Quinlan J R. Induction of decision trees[J]. Machine Learning, 1986, 1(1): 81-106. |
| [28] | Friedman J H. Stochastic gradient boosting[J]. Computational Statistics & Data Analysis, 2002, 38(4): 367-378. |
| [29] | Nelder J A, Wedderburn R W M. Generalized linear models[J]. Journal of the Royal Statistical Society: Series A, 1972, 135(3): 370-384. DOI:10.2307/2344614 |
| [30] | Breiman L. Random forests[J]. Machine Learning, 2001, 45(1): 5-32. DOI:10.1023/A:1010933404324 |
| [31] | Geurts P, Ernst D, Wehenkel L. Extremely randomized trees[J]. Machine Learning, 2006, 63(1): 3-42. DOI:10.1007/s10994-006-6226-1 |
| [32] | Qin K, Han X, Li D H, et al. Satellite-based estimation of surface NO2 concentrations over east-central China: a comparison of POMINO and OMNO2d data[J]. Atmospheric Environment, 2020, 224. DOI:10.1016/j.atmosenv.2020.117322 |
| [33] | Chen T Q, Guestrin C. XGBoost: a scalable tree boosting system[A]. In: Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining[C]. New York: ACM, 2016. 785-794. |
| [34] | Ke G L, Meng Q, Finley T, et al. LightGBM: a highly efficient gradient boosting decision tree[A]. In: Proceedings of the 31st International Conference on Neural Information Processing Systems[C]. Long Beach: Curran Associates Inc., 2017. 3149-3157. |
| [35] | Prokhorenkova L, Gusev G, Vorobev A, et al. CatBoost: unbiased boosting with categorical features[A]. In: Proceedings of the 32nd International Conference on Neural Information Processing Systems[C]. Montréal: Curran Associates Inc., 2018. 6639-6649. |
| [36] |
何月, 绳梦雅, 雷莉萍, 等. 长三角地区大气NO2和CO2浓度的时空变化及驱动因子分析[J]. 中国环境科学, 2022, 42(8): 3544-3553. He Y, Shen M Y, Lei L P, et al. Driving factors and spatio-temporal distribution on NO2 and CO2 in the Yangtze River Delta[J]. China Environmental Science, 2022, 42(8): 3544-3553. DOI:10.3969/j.issn.1000-6923.2022.08.008 |
| [37] |
赵雪, 沈楠驰, 李令军, 等. COVID-19疫情期间京津冀大气污染物变化及影响因素分析[J]. 环境科学, 2021, 42(3): 1205-1214. Zhao X, Shen N C, Li L J, et al. Analysis of changes and factors influencing air pollutants in the Beijing-Tianjin-Hebei region during the COVID-19 pandemic[J]. Environmental Science, 2021, 42(3): 1205-1214. |
| [38] |
易嘉慧, 何超, 杨璐, 等. COVID-19疫情期间全球气温和主要大气污染物浓度变化的空间关联[J]. 生态环境学报, 2022, 31(4): 740-749. Yi J H, He C, Yang L, et al. Spatial correlation between changes in global temperature and major air pollutants during the COVID-19 pandemic[J]. Ecology and Environmental Sciences, 2022, 31(4): 740-749. |
| [39] |
赵金环, 蔡坤, 李莘莘, 等. 新冠疫情对我国NO2排放影响的时空分析[J]. 中国环境科学, 2021, 41(1): 56-62. Zhao J H, Cai K, Li S S, et al. Spatiotemporal analysis on the impact of COVID-19 pandemic on NO2 emission in China[J]. China Environmental Science, 2021, 41(1): 56-62. DOI:10.3969/j.issn.1000-6923.2021.01.007 |
 2024, Vol. 45
2024, Vol. 45


