2. 河海大学港口海岸与近海工程学院, 南京 210098
2. College of Harbor, Coastal and Offshore Engineering, Hohai University, Nanjing 210098, China
港口是全球物流供应链的关键节点, 承担了全球货物运输约85%的周转量, 为促进社会经济发展做出了突出的贡献[1].然而, 繁忙的港口活动会产生大量的环境空气污染物, 从而诱发一系列公共卫生风险.特别是煤炭、矿物、建材等干散货在港口装卸、运输和存储的过程中会产生大量的颗粒物, 导致周边区域大气环境颗粒物浓度显著增加.部分干散货港口在作业过程中会导致周边区域颗粒物浓度提高40%[2].有研究表明, 与城市地区不同, 干散货港口PM10(空气动力学粒径≤10 μm的颗粒物)是主要的颗粒污染物, 对环境空气质量的影响较大[3].暴露于高浓度的PM10环境, 会对呼吸系统、免疫系统和内分泌系统等造成损害[4].因此, 有必要对PM10浓度的时变特征进行准确的预测, 以确保管理者可以提前采取针对性的防尘措施来控制PM10暴露水平, 可以降低港口人群的健康和经济风险, 还会对周边不同地区的经济发展平衡产生重大影响.
为预测环境空气中PM10浓度的时变特征, 时间序列回归是早期最常用的方法[5].根据PM10浓度历史统计数据的时间跨度, 可将其分为小时平均浓度、日平均浓度、月平均浓度和年平均浓度等不同类型.由于港口活动强度差异性的影响, 环境空气中PM10的小时平均浓度具有显著的波动性.鉴于短时暴露在PM10高浓度环境中会对人群健康产生显著的危害[6], 对于干散货港口, PM10小时平均浓度的准确预测显得更为重要. Perez等[7]利用圣地亚哥市PM10浓度监测数据的分析结果表明, 传统的时间序列回归模型很难捕捉PM10小时浓度的非线性变化特征, 神经网络模型的预测结果更准确, 但需要谨慎选择模型的输入变量.
随着机器学习方法的发展和应用, 有研究者开始使用支持向量回归(support vector regression, SVR)模型来研究PM10浓度变化的非线性特征.García等[8]对西班牙北部城市PM10月平均数据的预测分析表明, SVR比差分自回归移动平均模型具有更好的预测效果.黄萌等[9]利用兰州地区PM10浓度数据监测数据对SVR与BP(back propagation)神经网络模型进行了对比分析, 认为一般情况下SVR模型比BP神经网络模型具有更好的预测效果.为了提高SVR模型的求解速度, 冯晓秀等[10]提出了一个基于最小二乘法的SVR模型.为了提高SVR模型的泛化能力, 王平等[11]将小波变化与SVR结合, 以捕捉PM10浓度变化的突变特征并提高预测精度.Siwek等[12]利用华沙南部3 a的PM10浓度数据的分析结果表明, 将小波变换和SVR组合可以允许变量之间存在非线性关系, 从而显著提高SVR预测精度.利用土耳其的PM10小时浓度监测数据, Bozdag等[13]对4种机器学习模型预测性能的对比结果表明, 极端梯度提升(extreme gradient boosting, XGBoost)比SVR模型、Lasso模型和随机森林(random forest, RF)模型具有更好的预测性能.
近年来, 由于深度学习模型在解析非线性时间序列数据中潜在结构和特征的显著优势, 逐渐成为预测PM10小时浓度的重要方法.黄春桃等[14]对常见深度学习模型和机器学习模型预测效果的对比分析表明, 深度学习模型可以通过多个非线性映射层来解析数据内部隐含的关联关系, 具有更好的预测效果.Park等[15]利用韩国光阳集装箱港口的PM10浓度监测数据对长短时记忆神经网络(long short-term memory, LSTM)、递归神经网络(recursive neural network, RNN)和多元线性回归(multiple linear regression, MLR)模型的对比结果表明, LSTM模型具有更好的拟合和预测性能. Qiao等[16]利用中国6个城市PM10浓度监测数据的分析结果表明, 融合小波变换的LSTM可以降低时间序列数据的复杂性并提高预测性能, 但函数的选择和参数优化会显著影响模型的预测误差.鉴于卷积神经网络(convolutional neural networks, CNN)在提取空间特征方面的特长, Kurnaz等[17]认为CNN与RNN的组合模型可以更好地预测PM10的浓度变化特征. Zhang等[18]的研究结果表明, 基于CNN与LSTM的组合模型, 可以显著提高LSTM的预测效果.
针对城市范畴PM10浓度的预测研究, 为世界各地环境空气质量管理做出了重要贡献.然而, 针对港口尤其是干散货港口地区PM10浓度预测的研究较少.其主要原因可能是港口地区大气污染监测网络的建设较晚, 缺少预测研究所需的统计数据.近五年来, 为实现世界一流港口建设目标, 在交通运输部、发展改革委和生态环境部等9部门联合指导下, 全国干散货港口布设了大量空气质量在线监测系统, 使得港口PM10浓度预测研究具备了必要的基础和前提.然而, 特殊地形尺度和各种抑尘措施的叠加影响下, 港口地区具有复杂的气象环境[19], 常规城市环境中性能可靠的预测模型可能并不适用于干散货港口的PM10浓度预测.
因此, 针对干散货港口活动源强和环境气象因素耦合影响下PM10浓度特殊的时序非线性变化特征, 构建了一个级联CNN、LSTM和注意力机制(attention mechanism, AM)的深度学习组合预测模型(CLAF), 利用PM10浓度和特征气象因素监测数据来预测PM10的小时浓度.模型通过CNN和LSTM提取输入变量中隐藏的时序特征以及长期依赖性关系, 并根据AM为不同时间步的隐含状态分配权重, 以增强重要信息的影响.模型的优点在于无需作业活动强度清单、污染物输移过程以及稀释机制等难以获取的信息, 且允许不同时序输入数据之间存在非线性关联关系.通过准确预测PM10浓度峰值的突变特征, 模型可以为干散货港口实现本质防尘提供定量依据, 对港区居民的健康产生积极影响.
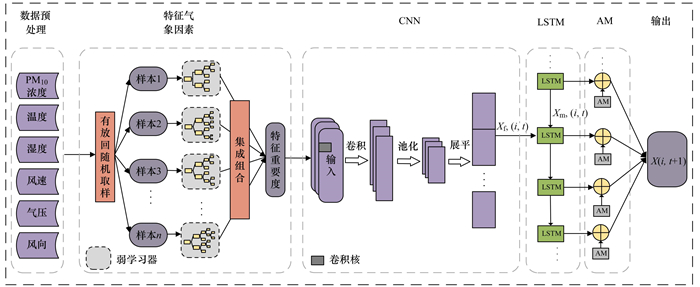
1 材料与方法为解析干散货港口特殊气候环境条件下PM10浓度变化的时间变化特征, 构建的预测模型包括:数据预处理、特征气象因素筛选、数据卷积、时间特征提取、权重分配及结果输出这6个部分, 如图 1所示.
|
图 1 PM10浓度预测方法结构示意 Fig. 1 Schematic of PM10 concentration forecasting methodology |
干散货港口PM10浓度除了受港口活动源强的影响外, 其传输、扩散和稀释过程会受到港口特殊气象条件的影响[19].因此, 用于预测研究的数据除了PM10浓度外, 还应包括同时监测的气象因素数据, 如温度、湿度、风速、气压和风向.对采集的PM10浓度和气象因素数据的预处理包括:①采用3σ原则去除监测数据中的异常值;②对于因为设备监测、数据传输或异常数据去除造成的缺少数据, 根据前后相邻时刻的数据使用线性插值方法进行补充;③为消除不同类型数据的量纲以及变化范围的差异的影响, 将每小时内的监测数据平均值作为小时浓度数据, 并采用最大最小归一化方法对各变量进行归一化处理后作为模型输入数据.
1.2 特征气象因素筛选由于PM10浓度和气象因素数据具有时序非线性变化特征, 很难确定其总体分布形态.同时, 考虑到PM10浓度和气象因素数据均采用在线监测系统成对采集, 本文使用RF特征重要性算法筛选影响PM10浓度变化的特征气象因素.作为一种多个决策树组合构成的集成学习算法, RF模型可以较好地分析数据的非线性特征[20].模型采用随机采样技术, 对原始数据进行多次有放回的抽样, 构建多个子样本决策树[21].在训练单个决策树时, 通过随机交换某个气象因素特征的值, 衡量交换特征值前后模型预测准确度的降低程度来评估该特征的重要性.变量特征j的重要性计算方法为:
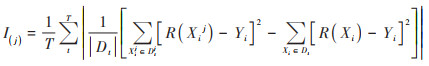
|
(1) |
式中, Xi和Yi为训练样本, I(j)为特征j的重要性, T为决策树数量, Xij为Xi交换特征j后的样本, Dt为决策树t未抽样的样本集, Dtj为第j维交换后形成的样本集, R(Xi)为样本Xi的预测输出.
本研究中, 用于训练RF模型的数据包括PM10浓度数据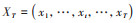
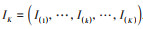
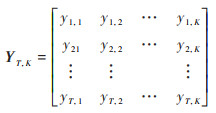
|
(2) |
鉴于CNN在提取时间序列数据隐藏特征方面的优势[22], 本文构建了1个包括卷积层、池化层和节点展开层的改进的一维CNN.
首先, 利用PM10浓度数据XT=(x1, …, xt, …, xT)和K个特征气象因素的监测数据YT, K构建T-L个滞后时刻为L的训练样本, 组成一个长为L, 宽为K+1, 深度为T-L的三维矩阵作为卷积层的输入数据.
其中, 第i个训练样本为:
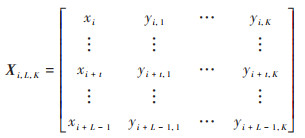
|
(3) |
其次, 将在卷积层利用卷积运算和激活函数从输入数据中提取特征.设卷积层的神经元数量为Nc, 其中第i个训练样本为Xi, L, K, 第j个神经元的权重矩阵为Wij, 偏置矩阵为bj.则Xi, L, K经过卷积后, 第j个神经元的输出值Xc(i, j)为:
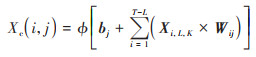
|
(4) |
式中, ϕ为激活函数, 可以选择Sigmoid函数、Tanh函数和ReLu函数等.由于ReLu函数不仅可以考虑非线性因素的影响, 且具有降低参数间依赖性的能力, 经过对比试验后设置ϕ为ReLu函数.
随后, 卷积操作处理的训练样本将通过池化层执行下采样操作, 以降低特征数据的维度并减少后续可学习参数的数量.基于最大池化, 可以将大小为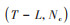
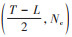
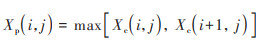
|
(5) |
最后, 池化后的特征矩阵将在展平层进行拼接操作, 作为LSTM的输入数据.展平层的输出结果Xf(i, t)为:
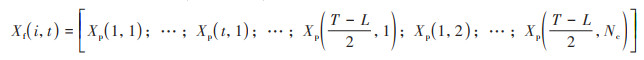
|
(6) |
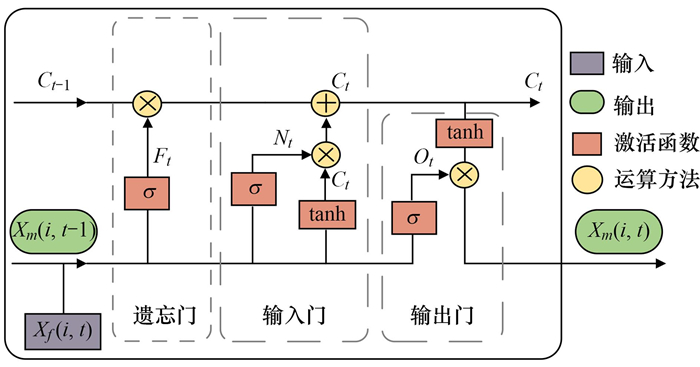
由于港口活动强度变化的连续性以及环境气象因素特征的特殊性, 港口PM10浓度的时序变化具有复杂的长期依赖特征.鉴于LSTM在解析时序数据中前序的状态信息关联性和长期依赖性特征的优势[23], 经过数据卷积后的训练样本将作为LSTM层的输入数据, 通过遗忘门、输入门和输出门筛选并融合, 如图 2所示.
|
图 2 LSTM结构示意 Fig. 2 Schematic of LSTM |
首先, 卷积后的输出数据Xf(i, t)作为LSTM当前的输入数据, 与LSTM在t-1时刻的输出结果Xm(i, t-1), 通过遗忘门Ft(Ft∈[0, 1])判断从前序的状态Ct-1中丢弃多少信息.遗忘门Ft的计算式为:
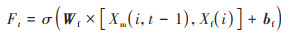
|
(7) |
式中, σ为Sigmoid函数, Wf为遗忘门权重矩阵, bf为遗忘门偏置矩阵.
随后, 将由输入门Nt决定当前输入Xf(i)中获取的瞬时状态中有哪些信息被更新到当前状态Ct中.记瞬时状态为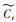
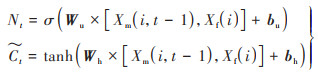
|
(8) |
式中, Wu输入门权重矩阵, bu为输入门偏置矩阵, Wh为待更新状态的权重矩阵, bh为待更新状态偏置矩阵, tanh为激活函数.通过遗忘门和输入门的综合控制, 当前状态Ct为:
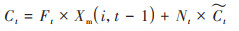
|
(9) |
最后, 输出门Ot将根据Xm(i, t-1)、Xf(i)和Ct, 输出PM10浓度的预测结果Xm(i, t)为:
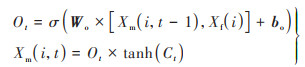
|
(10) |
式中, Wo为输出门权重矩阵, bo为输出门偏置矩阵.
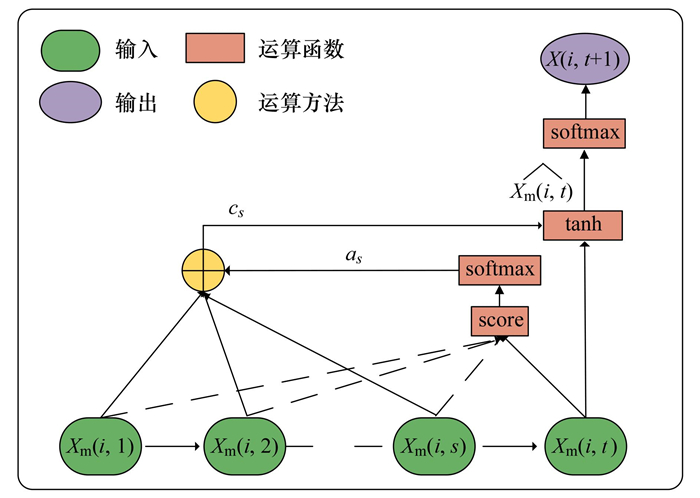
1.5 基于AM的权重分配及结果输出AM可以通过解析输入特征之间的内部相关性, 并根据前序的时刻特征重要性赋予不同权重来提高模型预测的精度[24].鉴于前序的时刻作业活动以及气象因素对港口PM10浓度扩散和传输变化的影响, 将通过AM为LSTM输出的不同时间步的预测结果赋予不同权重, 如图 3所示.
|
图 3 AM结构示意 Fig. 3 Schematic of AM |
首先, 对于LSTM输出的预测结果Xm(i, t), 利用score函数计算任意Xm(i, s)与Xm(i, t)的相关性值,
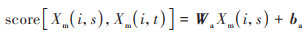
|
(11) |
式中, Wa和ba分别表示权重矩阵和偏差向量.
其次, 使用softmax函数计算Xm(i)与Xm(T-L)的相关性值, 得到注意力权重cs:
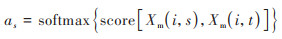
|
(12) |
根据AM赋予LSTM输出向量的权重以及LSTM输出向量的加权平均和, 得到前序的时刻相关性信息总结cs为:
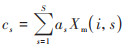
|
(13) |
由当前状态信息Xm(i, t)与前序的时刻相关性信息总结as可以得到AM连接层的输出结果Xm(i, t)为:
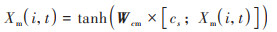
|
(14) |
式中, Wcm为权重矩阵.
根据Xm(i, t)可得到最终模型的预测结果X(i, t+1)为:
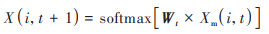
|
(15) |
式中, Wt为权重矩阵.
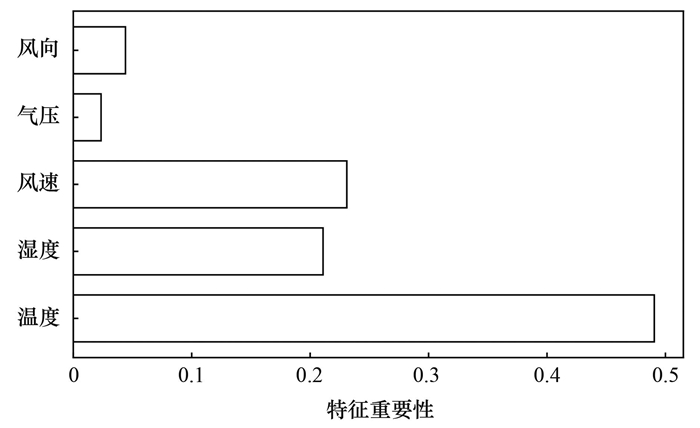
2 结果与讨论 2.1 数据特征为了对本研究提出的预测模型进行验证分析, 选择南京港西坝干散货港区内环境监测站的空气质量监测数据作为训练和测试样本.该港口的空气质量监测设备由港口管理部门于2022年安装, 由生态环境部门负责验收和定期标定监管, 监测数据为PM10浓度、温度、湿度、风速、风向和气压, 采样间隔为1min.剔除了设备试运行和标定期间可能存在的非正常监测数据后, 选择2023年2月1日至10月31日期间监测的数据用于本文分析.将PM10浓度和气象因素数据去除异常值和补充缺失值, 再将数据间隔调整为1 h后作为输入数据.利用网格搜索优化方法对RF模型进行训练后, 得到模型的超参数中决策树数量(nestimators)为100, 决策树最大深度(mdepth)为10.最终, 基于RF特征重要性算法得到影响PM10浓度变化的气象因素特征重要性排名结果如图 4所示.
|
图 4 气象因素特征重要性排名 Fig. 4 Feature importance ranking |
图 4中, 特征重要性系数值反映了不同气象因素对模型预测性能的贡献程度, 当系数值小于0.1时, 表明该特征对模型预测结果的贡献较低, 可在建模过程中忽略[25].从图 4中可知, 不同气象因素与PM10浓度变化的相关性存在显著的差异性.其中, 温度因素与PM10浓度的变化相关性最高, 其特征重要性接近0.5.而风向及气压与PM10浓度的变化相关性最小, 特征重要性低于0.1.然而, 在前期的研究中, 蔡春茂等[26]认为, 风向会显著影响城市PM10浓度的预测结果.这种差异的主要原因可能是在港口地区, 为了控制环境空气中PM10浓度, 管理者在港口四周布置的防风抑尘网影响了风向的变化造成的[27].在港区狭小的空间范围内, 特殊的大气环流在防风抑尘网的影响下, 导致港区内缺少明显的常风向来影响PM10浓度的变化.
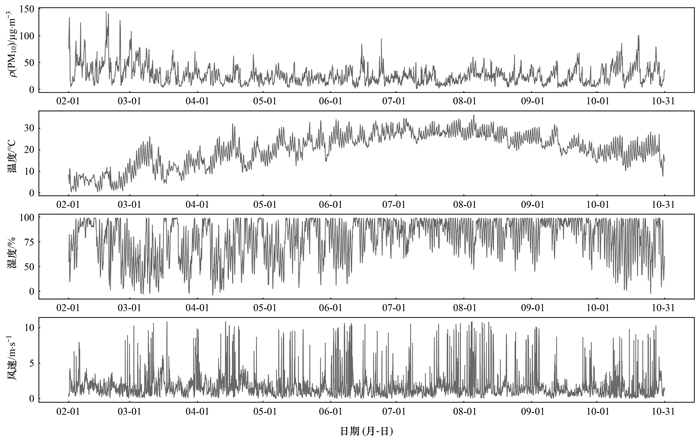
2.2 模型训练2023年2月1日至10月31日期间, PM10浓度与特征气象因素数据的时序变化特征如图 5所示.从PM10浓度和特征气象因素的波形特征可以看出, 具有显著的时序非线性特征, 且不同类型数据变化幅度的差异较大.因此, 进行模型训练时, 对监测数据进行归一化处理后, 将2月1日至10月4日数据作为训练集(5904组), 将10月5日至10月31日数据作为测试集(648组).模型训练的过程为, 训练样本作为输入数据通过CNN层提取特征信息后, 在LSTM层提取时序关联信息, 并根据AM层对不同时间步的输出分配权重, 进行加权求和后得到最终的预测结果.
|
图 5 2023年PM10浓度和特征气象因素的时序变化特征 Fig. 5 Time series variation characteristics of PM10 concentration and feature meteorological factors in 2023 |
在模型训练过程中, 对于构建的一维CNN层, 隐藏层和卷积核长度均设置为1.为了防止数据过拟合, CNN卷积超参数中卷积核的数量从3个常用参数(16, 32, 64)中选择, 窗口大小从3个常用参数(10, 20, 30)中选择.对于LSTM层, 层数的增加可以提高模型的数据拟合能力, 但过多的层数也容易带来过拟合的风险, 因此考虑模型训练时间和模型复杂度的影响, LSTM层数目同样设为1, 神经元同样从3个常用参数(16, 32, 64)中选择.对于AM层, 通过权重学习的方法确定最优参数.根据预测值与实际监测数据, 构建损失函数并使用自适应矩估计优化方法对网络权重进行迭代更新, 从而得到最优模型参数.自适应矩估计优化方法是一种自适应动量的随机优化方法, 可以利用梯度的一阶矩和二阶矩, 为不同的参数设计自适应学习速率.对于自适应矩估计优化的学习率的常用参数为0.001、0.01和0.1, 训练批次的常用参数为16, 32和64.利用训练样本中实际监测数据的反复训练, 以均方误差最小为目标, 综合考虑模型结构复杂度的影响, 最终确定CNN层卷积核个数为32个, 时间窗为10, LSTM神经元数为64个, 学习率为0.001, 训练批次为16.
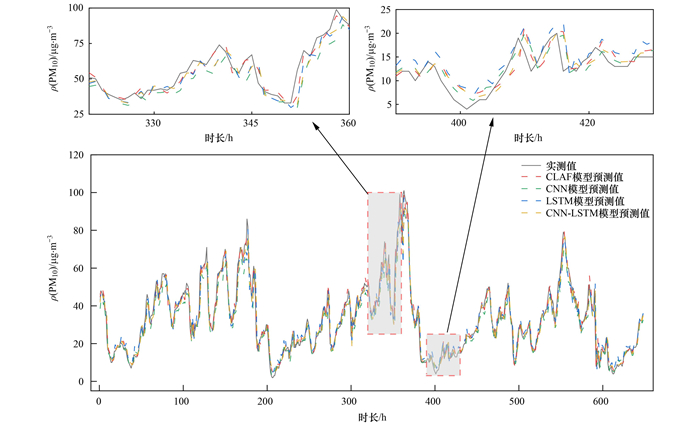
2.3 模型性能对比分析为了评估所提出模型的性能, 首先将组合模型CLAF与深度学习基本模型进行性能比较.即同样利用5 904组训练集对CNN、LSTM和CNN-LSTM分别进行训练后, 利用648组测试集将CLAF模型与基本模型预测结果进行对比, 如图 6所示.可以直观地发现, CLAF模型可以较好捕捉PM10浓度的时变特征, 与实测值的波形变化最接近.LSTM模型的预测值与实测值的偏离程度最大, CNN与CNN-LSTM模型捕捉PM10浓度变化的能力虽有所提高, 但当波形出现突变时与实测值的偏离程度仍较大.如图 6所示, 以第320~360 h较高PM10浓度及第390~430 h较低PM10浓度范围预测值与实测值波形对比为例, CLAF模型预测的浓度波形与峰值与实测值最接近.对于ρ(PM10)实测值大于75 μg·m-3范围的波形, CNN模型与LSTM模型的预测小于实测值.而对于ρ(PM10)实测值小于10 μg·m-3范围的波形, LSTM模型与CNN-LSTM模型预测值的波形具有显著的时间滞后性, CNN模型的预测显著小于实测值.
|
图 6 CLAF模型与基本模型的预测值对比 Fig. 6 Prediction results of the CLAF compared with basic models |
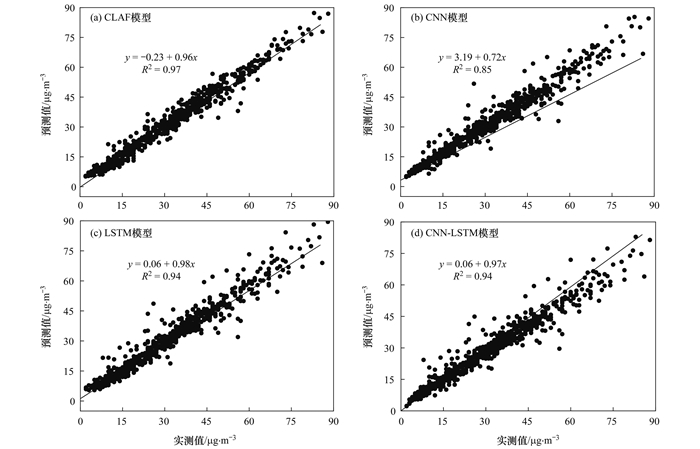
为了进一步分析不同模型的拟合性能, 选择常用的平均绝对误差(mean absolute error, MAE), 均方误差(mean square error, MSE)和拟合优度(R2)指标, 定量评价不同模型的性能差异性.MAE常用于判断实测值与预测值之间的差值, MSE可以进一步分析预测结果的离群情况, R2用于判断预测模型与监测数据的拟合程度.其中, MAE和MSE值越接近零则代表预测越接近真实监测值, R2越接近1代表预测模型的拟合程度越好.不同模型预测值与实测值的散点图及拟合回归曲线, 如图 7所示.从拟合优度R2评价指标可以看出, CLAF模型及基本模型的预测效果均较好, R2均超过了0.8.其中, CLAF模型的R2最高, 达到了0.97.而CNN模型的预测效果较差, R2仅为CLAF模型87%.
|
图 7 CLAF与基本模型的拟合性能对比 Fig. 7 Fitting performance of the CLAF compared with basic models |
此外, 从图 6和图 7可以直观地发现, 3个基本模型对于较高浓度PM10值(浓度大于45 μg·m-3)的预测效果均较差.CLAF模型与基本模型的MAE和MSE评价结果也表明(表 1), CLAF模型的预测效果最好, CNN模型的预测效果最差.其主要原因可能是由于CNN模型可以较好捕捉PM10浓度变化的特征因素, 但无法提取数据内部的长期依赖性关系.LSTM模型的MAE和MSE比CNN模型分别下降31.1%和99%, 可以发现不同时序数据之间的长期依赖性对港口PM10浓度变化的影响更显著.鉴于可以同时考虑PM10浓度时序数据中的特征因素与长期依赖性关系, CNN-LSTM比CNN和LSTM模型的预测效果更好.CALF模型通过注意力机制为时序影响因素的重要性赋予不同的权重, 进一步提高了港口PM10浓度的预测效果, MAE和MSE比CNN-LSTM模型分别降低了23.4%和95%.
|
|
表 1 不同模型预测精度和拟合性能评价指标 Table 1 Evaluation indexes of different models' prediction accuracy and fitting performance |
为了进一步评估CLAF模型的性能, 将其与城市范围预测效果较好的门控循环单元(gated recurrent unit, GRU)[14]、随机森林(RF)[28]以及梯度提升决策树(gradient boosting decision trees, GBDT)[29]模型进行对比.同样利用训练集确定模型的超参数后, 利用测试集数据对不同模型的性能进行评价.
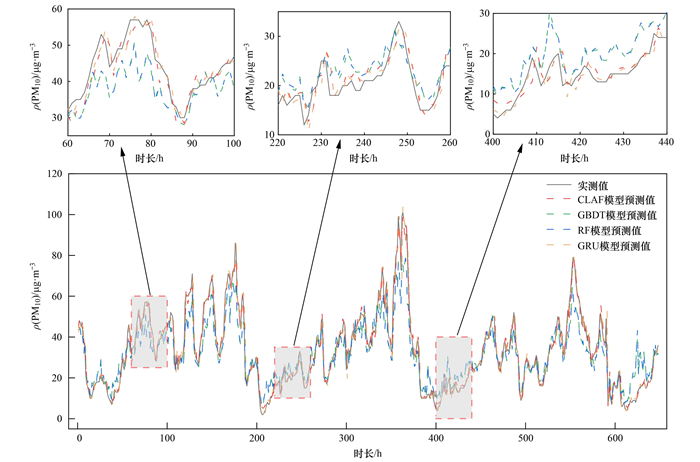
从模型预测值的时序变化特征(图 8)可以看出, RF与GBDT模型的预测值与实测值的偏离程度较大, 且预测的PM10浓度波形具有较显著的滞后性.GRU可以较好捕捉PM10浓度的变化趋势, 但对浓度峰值的预测值与实测值相差仍较大.CLAF模型不仅可以捕捉PM10浓度变化的非线性特征, 且对峰值的预测效果较好.不同模型的MAE、MSE和R2评价指标结果如表 1所示.
|
图 8 CLAF与常用模型的预测值对比 Fig. 8 Prediction results of the CLAF compared with commonly used models |
根据预测模型的定量评价指标可以看出, RF模型的预测效果较差, 可能是因为该模型仅采用Boost原理进行建模, 无法捕捉港口PM10浓度数据的时序关联性以及特征气象因素的影响.GBDT模型可以一定程度解析特征气象因素与PM10浓度变化的复杂非线性关系, MSE比RF模型降低了2.1%.GRU是LSTM的改进模型, 通过使用2个门控单元, 进一步提高了对时序数据中长期记忆问题的解析能力, MSE比LSTM降低了64.9%.然而, 这些模型的预测精度和相关性均小于CLAF模型.
从不同模型预测性能评价指标对比可以看出(表 1), 所有模型中RF模型的预测性能最低, CLAF模型可以将MAE降低56.9%, 将MSE降低81.02%, 将R2提高15.5%.GRU和CNN-LSTM模型的预测性能仅次于CLAF模型.与CNN-LSTM模型相比, CLAF模型可以将MAE降低23.4%, 将MSE降低95%, 将R2提高3.2%.由此可知, CLAF模型对CNN-LSTM模型预测性能的改进主要体现在预测精度, 对拟合性能的改善较小.其原因可能是AM层对于LSTM层输出变量赋予不同权重的策略, 主要影响预测结果与实测值在时序波形中峰值的偏离度, 对于波形时间滞后性的影响较小.
3 结论(1)鉴于PM10浓度和气象因素监测数据的随机性分布特征, 以及数据采集时间的成对关联性, 基于RF特征重要性相关系数, 筛选了影响港口PM10浓度变化的特征气象因素为温度、湿度和风速.鉴于地形尺度和防风抑尘措施的影响, 港口和城市范围内影响PM10浓度变化的特征气象因素存在显著的差异性, 将特征气象因素作为输入变量, 可以提高模型的预测性能.
(2)构建的组合预测模型可以利用CNN层提取输入变量的高维特征, 通过LSTM层解析时序数据中的长期依赖性关系, 并基于AM层为不同时间步的输出变量赋予不同权重, 使预测结果与实测值的特征波形的峰值偏离度和时间滞后性最小.
(3)对模型预测精度和拟合性能的定量评价结果表明, 现有的预测模型很难同时解析港口PM10浓度的时序非线性特征和长期记忆问题的影响, CLAF模型可以将MAE平均降低35.41%, 将MSE平均降低63.51%, 将R2平均提高9.45%.
| [1] | Iris Ç, Lee Lam J S. A review of energy efficiency in ports: operational strategies, technologies and energy management systems[J]. Renewable and Sustainable Energy Reviews, 2019, 112: 170-182. DOI:10.1016/j.rser.2019.04.069 |
| [2] | Köse S. Measurement and modelling of particulate matter emissions from harbor activities at a port area: a case study of Trabzon, Turkey[J]. Journal of ETA Maritime Science, 2020, 8(4): 286-301. DOI:10.5505/jems.2020.49389 |
| [3] |
徐文文, 殷承启, 许雪记, 等. 江苏省内河船舶大气污染物排放清单及特征[J]. 环境科学, 2019, 40(6): 2595-2606. Xu W W, Yin C Q, Xu X J, et al. Vessel emission inventories and emission characteristics for inland rivers in Jiangsu province[J]. Environmental Science, 2019, 40(6): 2595-2606. |
| [4] |
黄琳, 刘迪, 蔡东杰, 等. 广州市多污染物联合暴露的健康效应评估[J]. 中国环境科学, 2022, 42(11): 5418-5426. Huang L, Liu D, Cai D J, et al. Health risk assessment of exposure to multiple pollutants in Guangzhou[J]. China Environmental Science, 2022, 42(11): 5418-5426. DOI:10.3969/j.issn.1000-6923.2022.11.048 |
| [5] |
程文娜. PM10浓度的时间序列模型及预测[J]. 科学技术与工程, 2010, 10(9): 2260-2262, 2266. Cheng W N. Time series model and prediction of PM10 concentration[J]. Science Technology and Engineering, 2010, 10(9): 2260-2262, 2266. DOI:10.3969/j.issn.1671-1815.2010.09.051 |
| [6] | Minguillón M C, Arhami M, Schauer J, et al. Seasonal and spatial variations of sources of fine and quasi-ultrafine particulate matter in neighborhoods near the Los Angeles-Long Beach harbor[J]. Atmospheric Environment, 2008, 42(32): 7317-7328. DOI:10.1016/j.atmosenv.2008.07.036 |
| [7] | Perez P, Reyes J. An integrated neural network model for PM10 forecasting[J]. Atmospheric Environment, 2006, 40(16): 2845-2851. DOI:10.1016/j.atmosenv.2006.01.010 |
| [8] | García Nieto P J, Sánchez Lasheras F, García-Gonzalo E, et al. PM10 concentration forecasting in the metropolitan area of Oviedo (Northern Spain) using models based on SVM, MLP, VARMA and ARIMA: a case study[J]. Science of the Total Environment, 2018, 621: 753-761. DOI:10.1016/j.scitotenv.2017.11.291 |
| [9] |
黄萌, 王颖, 秦闯, 等. 基于SVR和BPNN的兰州市PM10质量浓度预测对比[J]. 兰州大学学报(自然科学版), 2020, 56(5): 659-665. Huang M, Wang Y, Qin C, et al. PM10 mass concentration prediction in Lanzhou based on SVR and BPNN[J]. Journal of Lanzhou University (Natural Sciences), 2020, 56(5): 659-665. |
| [10] |
冯晓秀, 高志文, 李风军, 等. 基于LS-SVR、BP-ANN和MLR模型的PM10浓度预测[J]. 中国环境监测, 2014, 30(6): 138-141. Feng X X, Gao Z W, Li F J, et al. Prediction of PM10 concentrations based on LS-SVR, BP-ANN and MLR models[J]. Environmental Monitoring in China, 2014, 30(6): 138-141. |
| [11] |
王平, 张红, 秦作栋, 等. 基于wavelet-SVM的PM10浓度时序数据预测[J]. 环境科学, 2017, 38(8): 3153-3161. Wang P, Zhang H, Qin Z D, et al. PM10 concentration forecasting model based on wavelet-SVM[J]. Environmental Science, 2017, 38(8): 3153-3161. |
| [12] | Siwek K, Osowski S, Sowinski M. Evolving the ensemble of predictors model for forecasting the daily average PM10 [J]. International Journal of Environment and Pollution, 2011, 46(3-4): 199-215. |
| [13] | Bozdağ A, Dokuz Y, Gökçek Ö B. Spatial prediction of PM10 concentration using machine learning algorithms in Ankara, Turkey[J]. Environmental Pollution, 2020, 263. DOI:10.1016/j.envpol.2020.114635 |
| [14] |
黄春桃, 范东平, 卢集富, 等. 基于深度学习模型的广州市大气PM2.5和PM10浓度预测[J]. 环境工程, 2021, 39(12): 135-140. Huang C T, Fan D P, Lu J F, et al. Prediction of PM2.5 and PM10 concentration in Guangzhou based on deep learning model[J]. Environmental Engineering, 2021, 39(12): 135-140. |
| [15] | Park S Y, Woo S H, Lim C. Predicting PM10 and PM2.5 concentration in container ports: a deep learning approach[J]. Transportation Research Part D: Transport and Environment, 2023, 115. DOI:10.1016/j.trd.2022.103601 |
| [16] | Qiao W B, Wang Y N, Zhang J Z, et al. An innovative coupled model in view of wavelet transform for predicting short-term PM10 concentration[J]. Journal of Environmental Management, 2021, 289. DOI:10.1016/j.jenvman.2021.112438 |
| [17] | Kurnaz G, Demir A S. Prediction of SO2 and PM10 air pollutants using a deep learning-based recurrent neural network: case of industrial city Sakarya[J]. Urban Climate, 2022, 41. DOI:10.1016/j.uclim.2021.101051 |
| [18] | Zhang J X, Li S Y. Air quality index forecast in Beijing based on CNN-LSTM multi-model[J]. Chemosphere, 2022, 308. DOI:10.1016/j.chemosphere.2022.136180 |
| [19] |
秦廷双, 何红弟. 港口NO2、PM10与天气因素的多重分形研究[J]. 环境工程, 2017, 35(2): 104-110. Qin T S, He H D. Multifractal analysis of NO2, PM10 and meteorology factors in port[J]. Environmental Engineering, 2017, 35(2): 104-110. |
| [20] | Chen M, Bai J C, Zhu S W, et al. The influence of neighborhood-level urban morphology on PM2.5 variation based on random forest regression[J]. Atmospheric Pollution Research, 2021, 12(8). DOI:10.1016/j.apr.2021.101147 |
| [21] | Li Z Y, Yim S H L, Ho K F. High temporal resolution prediction of street-level PM2.5 and NOx concentrations using machine learning approach[J]. Journal of Cleaner Production, 2020, 268. DOI:10.1016/j.jclepro.2020.121975 |
| [22] | Liu H, Mi X W, Li Y F. Smart deep learning based wind speed prediction model using wavelet packet decomposition, convolutional neural network and convolutional long short term memory network[J]. Energy Conversion and Management, 2018, 166: 120-131. DOI:10.1016/j.enconman.2018.04.021 |
| [23] | Chen Y R, Cui S H, Chen P Y, et al. An LSTM-based neural network method of particulate pollution forecast in China[J]. Environmental Research Letters, 2021, 16(4). DOI:10.1088/1748-9326/abe1f5 |
| [24] | Nandi A, De A, Mallick A, et al. Attention based long-term air temperature forecasting network: ALTF Net[J]. Knowledge-Based Systems, 2022, 252. DOI:10.1016/j.knosys.2022.109442 |
| [25] | Guo J Q, Yang L, Bie R F, et al. An XGBoost-based physical fitness evaluation model using advanced feature selection and Bayesian hyper-parameter optimization for wearable running monitoring[J]. Computer Networks, 2019, 151: 166-180. |
| [26] |
蔡春茂, 何红弟. 基于气象因素的PM10浓度预测[J]. 大气与环境光学学报, 2019, 14(3): 191-200. Cai C M, He H D. Prediction of PM10 concentration based on meteorological factors[J]. Journal of Atmospheric and Environmental Optics, 2019, 14(3): 191-200. |
| [27] |
岳霖, 岳田, 杜振辉. 港口工程散货堆场防风抑尘网结构设计[J]. 水运工程, 2022(S1): 109-114. Yue L, Yue T, Du Z H. Structural design of wind and dust suppression nets for bulk cargo yards in port engineering[J]. Port & Waterway Engineering, 2022(S1): 109-114. |
| [28] |
姚红岩, 施润和. 基于周边站点优化选取的随机森林PM2.5小时浓度预测研究[J]. 环境科学学报, 2021, 41(4): 1565-1573. Yao H Y, Shi R H. Research on hourly PM2.5 concentration prediction of random forest based on optimal selection of surrounding stations[J]. Acta Scientiae Circumstantiae, 2021, 41(4): 1565-1573. |
| [29] |
肖宇. 基于多机器学习算法耦合的空气质量数值预报订正方法研究及应用[J]. 环境科学研究, 2022, 35(12): 2693-2701. Xiao Y. Research and application of an ensemble forecasting method based on coupled multi-machine learning algorithms[J]. Research of Environmental Sciences, 2022, 35(12): 2693-2701. |
 2024, Vol. 45
2024, Vol. 45


