2. 中国地质调查局乌鲁木齐自然资源综合调查中心, 乌鲁木齐 830057;
3. 中国自然资源航空物探遥感中心, 北京 100083;
4. 长安大学土地工程学院, 西安 710054;
5. 中国地质调查局西安矿产资源调查中心, 西安 710100
2. Center of Urumqi Comprehensive Survey Natural Resources, China Geological Survey, Urumqi 830057, China;
3. China Aero Geophysical Survey and Remote Sensing Center for Natural Resources, Beijing 100083, China;
4. School of Land Engineering, Chang'an University, Xi'an 710054, China;
5. Xi'an Mineral Resources Survey Centre, China Geological Survey, Xi'an 710100, China
土壤生态系统作为环境要素的核心成分以及陆地生态系统物质能量循环的枢纽, 是各类污染物的主要承载体[1]. 土壤生态安全是土地资源高效利用的基础, 是实现国家粮食安全、经济安全和生态安全的基础[2]. 其中镉(Cd)、铬(Cr)、汞(Hg)、镍(Ni)、铜(Cu)、锌(Zn)、铅(Pb)以及砷(As)等生物毒性显著的元素是环境污染防治的重点[3]. 而农田土壤长期受到人类活动的影响, 尤其高剂量农药化肥施用、污灌及工矿排放等不合理行为加剧了重(类)金属的累积作用, 对农田土壤生态安全、粮食安全及人体健康具有较高风险[4].
传统的土壤重金属调查工作主要通过大量的土壤样品采集实现, 且需要开展繁重的分析测试工作, 经费投入大、工作时间长、工作效率低是限制其发展的重要因素[5]. 机器学习是一门多领域交叉的学科, 其本质是让计算机在数据中学习规律, 并根据所得到的规律对未知数据进行预测[6, 7], 包括聚类、分类、决策树、神经网络和深度学习等算法, 且广泛应用于土壤科学中[8, 9]. 通过土壤重金属数据及相关辅助变量的有效整合, 构建线性或非线性的模型进行土壤重金属的空间分布预测[10, 11]. 金昭等[12]利用9种机器学习模型, 对山东省中部土壤重金属进行空间分布预测并对比其精度. 刘烨坤等[13]采用机器学习中的LASSO回归模型、AdaBoost算法和随机森林模型, 对经过主成分分析的数据进行模型训练, 实现了土壤重金属元素镍和钯的定量分析. Guan等[14]基于酒泉地区土壤重金属实测数据以及多光谱数据, 采用逐步多元线性回归和偏最小二乘回归相结合的方法预测该区土壤中重金属的含量和分布. Sergeev等[15]将机器学习与地统计学方法相结合, 进一步提高了对土壤重金属空间分布的预测精度. 虽然已有研究工作在重金属含量的统计分析和预测方面取得了一定进展, 但目前相关研究主要集中于内地相关省份[16, 17], 对于西北干旱区相关研究较少, 且研究多聚焦于土壤重金属含量[18, 19]和空间分布预测[20, 21], 对土壤重金属健康风险预测的研究较缺乏[22].
塔里木盆地面积巨大, 绿洲区农业活动频繁, 通过传统采样方法实现区域土壤重金属多年连续监测可行性较低, 需要探索基于机器学习的土壤重金属含量预测及评价方法. 因此, 本文采用多元线性回归(LR)、神经网络(BP)、随机森林(RF)、支持向量机(SVM)和基于径向基函数神经网络(RBF)这5种经典机器学习模型, 基于塔里木盆地东缘绿洲区644个表层土壤样品中As、Cr、Cd、Cu、Zn、Hg、Pb和Zn等8类元素含量, 分析研究区土壤重(类)金属元素含量特征, 遴选Cd元素作为重金属污染代表性元素, 按照7∶3划分训练集与验证集, 基于优化特征后的变量开展区域土壤Cd元素含量预测及健康风险评价, 筛选最优拟合模型.
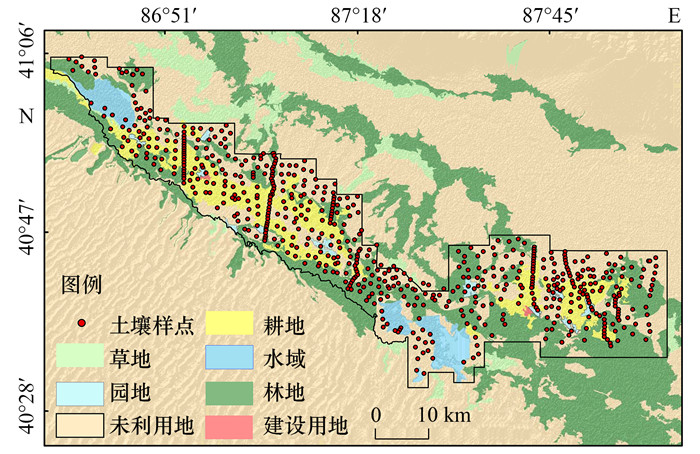
1 材料与方法 1.1 研究区概况选取新疆生产建设兵团第二师塔里木垦区为研究区(图 1), 该区位于塔里木盆地东缘、塔里木河中游, 地理坐标为86°19′~88°02′E, 40°25′~41°09′ N. 行政区划涉及31团、33团和34团共3个团场, 总面积约2 215.52 km2. 该地区属暖温带干旱半干旱气候, 具有光能丰富、日照充足和气候干燥的特点, 年平均气温5.50 ℃, 年平均降水量64.10 mm左右. 区域主要地貌类型为缓坡丘陵和沙地, 地势由西北向东南倾斜, 坡降较缓, 整体较为平坦. 主要成土母质为黄土;主要土类有盐土、风沙土、潮土和粗骨土等;自然植被以多枝柽柳(Tamarix ramosissima Ledeb)、芦苇[Phragmites australis(Cav.)Trin. ex Steud]、胡杨(Populus euphratica Oliv)及盐节木[Halocnemum strobilaceum(Pall.)M. Bieb]等为主. 研究区以灌溉农业为主, 土地利用类型主要为耕地、荒地、林地和园地, 经济作物主要为棉花、香梨和红枣等. 区内交通便利, 市县乡道路畅通发达, 国道218自北向南从研究区穿过, 是南疆的重要交通枢纽之一.
|
图 1 研究区土地利用及采样点位置 Fig. 1 Land use of the study area and the sampling sites |
2021年6月, 按照分层抽样和随机布点相结合的方式在研究区内布设土壤采样点644个, 采样深度为0~30 cm, 采样密度近1点·(4 km2)-1, 对各采样点按照“X”形方式每5个点混合成1件土壤样品(约重1 kg). 实际采样过程中, 避开灌排沟渠、垃圾堆积点、肥料厂站等主要干扰源. 同时, 记录采样点及对应样地的基本信息, 包括点位坐标、作物类型、田块面积、作物熟制等. 将所有采集的土壤样品去除石子、植物残体等杂物, 放置室内自然风干后经人工粉碎、研磨, 过20目尼龙筛备用.
土壤样品的分析测试参照国土资源部发布的《区域地球化学样品分析方法》(DZ/T 0279-2016)标准, 测定As、Cd、Cr、Hg、Cu、Zn、Ni和Pb元素的含量, 测试方法主要为原子荧光光谱法、等离子体质谱法及原子吸收光谱法, 实验设备主要为等离子体质谱仪(Xseries Ⅱ, 美国赛默飞世尔)、荧光光谱仪(XP+, 美国赛默飞世尔)和原子吸收分光光度计(Z-2010, 日本日立), 以上分析测试工作均由新疆有色地质勘查局分析测试中心完成. 验证工作采用平行样测量值与标准值的对数误差和相对标准偏差来控制测试分析的准确度和精密度, 结果均满足地球化学评价样品分析技术规范要求.
1.3 模型方法 1.3.1 线性回归模型(linear regression, LR)线性回归模型是一种用于建立变量之间线性关系的统计模型[23]. LR通过将一个或多个自变量与一个连续的因变量之间的关系表示为直线方程, 进而预测因变量. 普通最小二乘回归模型(ordinary least squares, OLS)是一种常见的线性回归模型, 用于寻找最佳拟合直线, 使得预测值与实际观测值的残差平方和最小化. OLS回归模型的数学表达式为:
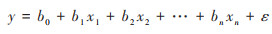
|
(1) |
式中, y表示因变量, x1, x2, …, xn表示自变量, b0, b1, b2, …, bn表示模型的参数, ε表示误差项.
1.3.2 随机森林算法(random forest, RF)RF由传统的分类和回归树(CART)发展而来, 具有预测效率高且抗过拟合等优势[24]. RF根据bootstrap重采样方法, 从原始训练集中抽取若干大小相同的子集, 并利用每个子集训练一棵决策树;在每棵决策树上, 选取子样本中的最优变量进行节点分割. RF的最终预测结果由所有树的结果进行平均得到, 其计算公式为:
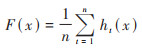
|
(2) |
式中, F(x)表示RF的最终预测结果;ht(x)表示第t棵决策树的回归预测结果. 本研究中决策树数目设置为500, 最小叶子树为5.
1.3.3 支持向量机(support vector machine, SVM)SVM方法可以较好地解决小样本、非线性、高维数据和局部极小点等分类和回归的实际问题, 并在很大程度上克服“维数灾难”和“过学习”等问题[25]. 该方法利用核函数进行非线性映射, 将已知空间变换到高维空间, 从而在高维空间进行样本的线性分类和回归. 当用于回归时, 建立的模型为支持向量机回归模型. SVM方法在特征空间中构建最优分类面, 用少数支持向量代替整个样本空间, 使得计算最终决策函数时算法更简便, 且有较好的“鲁棒性”. 其函数表达为:
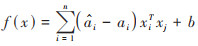
|
(3) |
引入核函数, 将Φ(x)代替x, 得到含核函数的最终模型为:
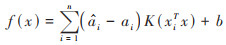
|
(4) |
式中, 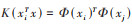
BP算法的主要思想是把学习过程分为两个阶段, 即正向传播和反向传播[26]. 正向传播时, 输入的样本从输入层经过隐单元一层一层进行处理, 通过所有的隐含层之后, 则传向输出层;在逐层处理的过程中, 每一层神经元的状态只对下一层神经元的状态产生影响. 在输出层把现行输出和期望输出进行比较, 如果现行输出不等于期望输出, 则进入反向传播过程. 反向传播时, 将实际值与网络输出之间的误差沿原来的连接通路返回, 通过修改各层神经元的连接权重使误差减小, 然后再转入正向传播过程, 如此反复计算, 直到误差小于设定值为止.
建立BP神经网络, 隐含层传递函数使用正切“S”型函数tansig, 输出层使用对数“S”型函数logsig, 神经网络的扩展常数为1.0. 训练函数采用动态自适应BP算法, 并制订停止准则:目标误差精度和训练代数. 训练误差精度设定为满足条件的1×e-6, 训练次数为1 000次. tansig以及logsig公式如下:
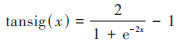
|
(5) |
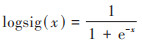
|
(6) |
径向基函数神经网络, 也称局部感受域神经网络[27]. RBF神经网络的结构与BP网络类似, 是一种以函数逼近理论为基础的前馈型人工神经网络, 网络模型的拓扑结构分为输入层、隐含层、输出层, RBF网络用RBF作为隐含单元构成隐含层空间, 从输入层空间到隐含层空间的变化是通过基函数进行非线性映射, 而从隐含层空间到输出层空间的变化是线性的, 隐含层单元的变换函数是一种径向对称的非线性函数.
RBF网络最常用的基函数是高斯函数, 其对输入信号在局部产生响应, 即当输入信号靠近基函数的中央范围时, 隐含层节点产生较大输出, RBF网络具有良好局部逼近能力. 输入层节点分别表示经归一化处理后的各影响因子, 输出层节点采用简单的线性传递函数, 表示经归一化处理后的输出值.
本文采用的径向基函数是高斯函数, 其激活函数可表示为:
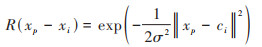
|
(7) |
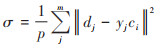
|
(8) |
式中, 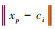
径向基函数神经网络的结构可得到网络的输出为:
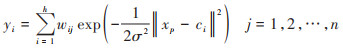
|
(9) |
式中, xp表示第p个输入样本, p = 1, 2, 3, …, n, n表示样本总数;ci表示网络隐含层节点的中心, wij表示隐含层到输出层的连接权值, i = 1, 2, 3, …, h, 表示隐含层节点数;yi表示与输入样本对应的网络的第i个输出节点的实际输出.
1.4 精度评价在进行重金属含量预测时, 按照70%和30%比例提取土壤样点数据分别作为训练集和验证集. 首先利用训练集与特征变量进行建模, 然后对验证集的预测值和实测值比较, 通过计算验证集的拟合优度(R2)、平均绝对误差(MAE)、均方根误差(RMSE)和平均偏差误差(MBE)评价预测精度[12]. R2、RMSE、MAE和MBE的计算公式如下:
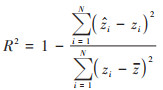
|
(10) |
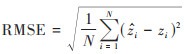
|
(11) |
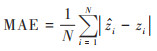
|
(12) |
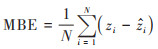
|
(13) |
式中, N表示样点个数;zi和 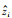
人类健康风险评价模型是一种用于评估某种有害的因素对人体健康的损伤和可能性的方法, 包括危害识别、剂量-反应关系、暴露评估和风险表征这4个步骤[28], 是美国环境保护署(USEPA)推荐的土壤重金属暴露风险评估方法. 前人研究表明[29], 土壤重金属元素进入人体的途径主要包括:手-口、呼吸及皮肤接触这3种方式, 具体计算公式为:
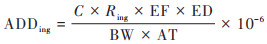
|
(14) |
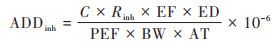
|
(15) |
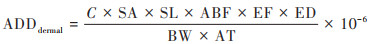
|
(16) |
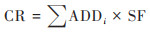
|
(17) |
式中, ADDing、ADDinh和ADDdermal分别表示每日平均经口摄入、呼吸摄入及皮肤接触的暴露量, 单位为mg·(kg·d)-1;ADDi表示不同途径的暴露量;CR表示致癌风险系数, USEPA推荐的致癌风险系数(carcinogenic risk, CR)分级标准为[29]:CR > 10-4时, 致癌风险较高;10-6 < CR < 10-4时, 可接受水平的致癌风险;CR < 10-6时无致癌风险. 公式(14)~(16)评价暴露参数见表 1.
|
|
表 1 健康风险评价暴露参数 Table 1 Exposure parameters for health risk evaluation |
2 结果与分析 2.1 土壤重金属统计分析
研究区8种土壤重金属的统计值见表 2, ω(As)、ω(Hg)、ω(Cr)、ω(Ni)、ω(Cu)、ω(Zn)、ω(Cd)和ω(Pb)均值分别为10.06、0.02、42.3、22.26、18.89、53.63、0.14和17.63 mg·kg-1. 除Cd元素外, 其他元素的含量均值未超过新疆土壤重金属背景值[30], 其中Cd元素含量均值是其土壤背景值的1.17倍, 说明研究区土壤Cd元素较为富集, 是区内土壤重金属污染的主要因子. 同时, Cd元素的偏度为3.31, 峰度为31.02, 变异系数为0.31, 处于正偏态、中等变异水平, 表明研究区土壤Cd元素的富集除受到成土母质、沉积环境的影响外, 还受到人为活动的影响. 因此, 本文选取Cd元素作为研究区土壤重金属的代表性元素, 开展基于机器学习的含量预测、健康风险评价相关研究工作.
|
|
表 2 土壤重金属含量特征统计(n = 644) Table 2 Characteristic statistics of soil heavy metal content (n = 644) |
2.2 变量优选
本文所选研究区位于塔里木盆地东缘, 区域特色显著, 农业活动强烈, 受城市化进程影响农田分布破碎化严重[31]. 依据前人已有研究成果[32], 结合研究区实际, 按照代表性和易取易用等选取原则, 综合考虑自然环境(地形地貌、气候环境、土壤属性等)、生态状况(归一化植被指数和净初级生产力等)、人类活动(农业施肥等)和社会经济(土地利用等)这4大类因素, 梳理了土壤质地、pH值、降水、地温及地表粗糙度等18项辅助变量(表 3).
|
|
表 3 变量信息 Table 3 Variable information |
前人研究发现[33], 数据集中存在大量冗余的变量时不仅有损模型性能, 而且还会带来建模成本的提升. 为进一步提高机器学习模型预测的准确度, 减少过拟合几率, 同时降低模型训练时长, 需要根据每个辅助变量对预测结果的重要性程度进行特征优选, 确定最佳的预测变量集.
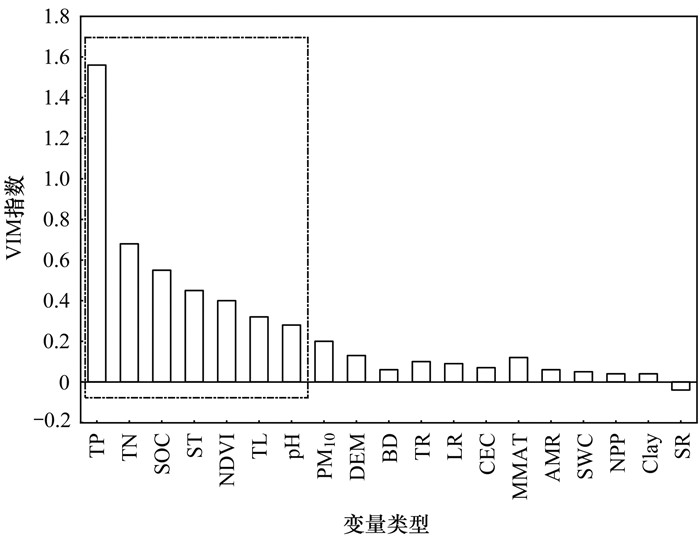
本文采用VIM(variable importance measure)指数对所有变量的重要性进行排序, 确定对预测结果影响最大的因子集[34]. VIM指数是随机森林模型中用来评估每个特征(变量)对模型预测能力的贡献程度的指标. VIM指数越高, 表示该特征对模型的预测结果影响越大. 结果如图 2所示, 各变量重要性依次为:TP > TN > SOC > ST > NDVI > TL > pH > PM10 > DEM > BD > TR > LR > CEC > MMAT > AMR > SWC > NPP > Clay > SR. 为保证模型既具有较低的复杂度, 同时具备较高的计算效率, 本文确定了TP、TN、SOC、ST、NDVI、TL和pH等7类组成最佳变量集.
|
虚线框内变量类型为优选后确定的最佳变量集 图 2 变量重要性排序 Fig. 2 Variable importance ranking |
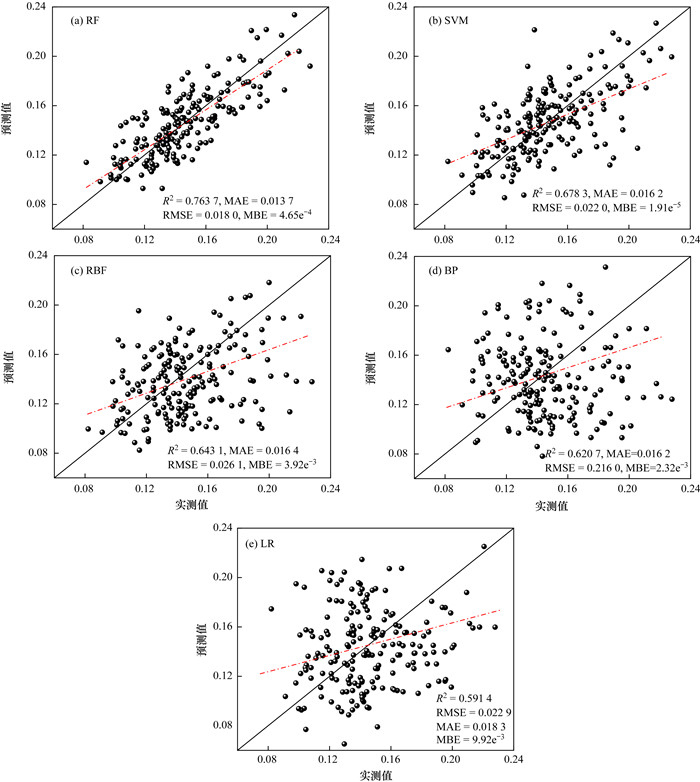
本文所采用的机器学习模型均通过Matlab 2021a实现, 按照7∶3比例随机选取训练集与验证集数据, 以训练集(n = 450)的最佳变量集与土壤Cd元素实测数据构建并训练5种机器学习模型;以验证集(n = 194)的最佳变量集作为输入变量, 分别利用5种模型进行土壤Cd元素含量预测, 得到各模型下预测结果的R2、RMSE、MAE和MBE精度值. 由图 3可知, RF模型预测Cd的R2值最大(0.763 7);其次为SVM模型, R2为0.678 3;LR模型对Cd元素预测的R2最小(0.591 4). 各模型预测Cd的RMSE中, LR模型RMSE值最大(0.022 9), RF模型RMSE值最小(0.018 0). MAE的最大值为0.018 3, 为LR模型对Cd的预测;最小值为0.013 7, 为RF模型对Cd的预测. MBE的最大值为9.92e-3, 为LR模型对Cd的预测;最小值为1.91e-5, 为SVM模型对Cd的预测. 前人研究成果表明[35, 36], R2越大, RMSE、MAE和MBE越小, 模型的预测效果越好.
|
黑色实线为1∶1等值线, 红色虚线为散点拟合线 图 3 不同机器学习模型的土壤Cd元素验证集散点图 Fig. 3 Scatterplot of soil cadmium validation set for various machine learning models |
结合不同机器学习模型的土壤Cd元素验证集散点图可知(图 3), 土壤中Cd元素含量实测值与RF模型的预测值拟合效果最佳, 其次为SVM模型, LR模型的预测结果最差. 因此, 5种机器学习模型中, RF模型对研究区土壤Cd元素含量预测效果最佳, 可作为首选模型;SVM模型对于区内土壤中Cd元素的预测效果仅次于RF模型, 可作为备选模型. 同时, 相比于非线性模型(RF、SVM、BP和RBF), 线性模型(LR)对土壤重金属的空间预测精度偏低.
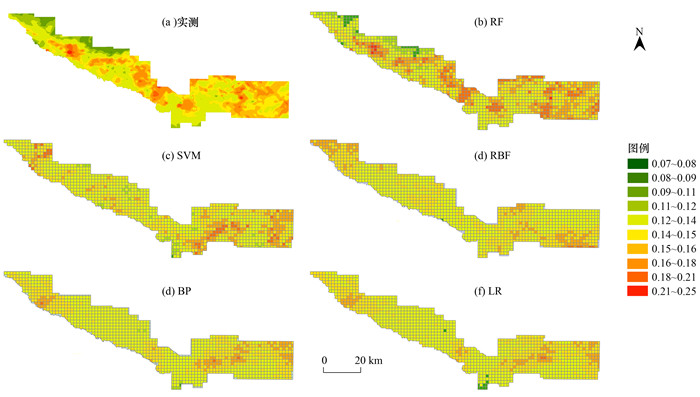
2.4 空间分布对比将TP、TN、SOC、TL、NDVI、pH和ST等优选后的变量作为输入集导入训练后的机器学习模型中, 得到各机器学习模型预测的Cd元素含量值[37], 绘制了基于5种机器学习模型的研究区土壤Cd元素的空间分布预测[图 4(b)~4(f)], 同时利用研究区644个点位的实测Cd元素数据, 绘制了土壤中Cd元素的实测含量空间分布[图 4(a)]. 对比可知, RBF、BP及LR等3种模型对土壤Cd元素含量的预测值较为分散, 具体表现为:图 4(d)~4(f)中Cd元素的含量高值区不够显著;RF、SVM模型的预测结果高值区呈斑块状, 具有一定的环带状分布格局, Cd元素含量的预测值相对集中, 其中以RF模型的预测结果最好, 其空间分布预测图的高、低值区与实测图具有良好的一致性.
|
图 4 土壤Cd元素实测值与不同机器学习模型预测值的空间分布 Fig. 4 Spatial distribution of measured values of soil Cd and predicted values of different machine learning models |
Cd元素是自然界中广泛存在的有毒金属, 2012年被世界卫生组织国际癌症研究机构IARC列为Ⅰ类致癌物[38], 因此本次研究使用致癌物风险评估模型[29], 对土壤Cd的健康风险进行评价. 通过计算得到研究区土壤Cd健康风险评价结果:成人ADDing的最大值为0.38×10-6、最小值为0.04×10-6和均值为0.08×10-6;成人ADDinh的最大值为0.41×10-16、最小值为0.04×10-16和均值为0.08×10-16;成人ADDdermal的最大值为0.33×10-8、最小值为0.03×10-8和均值为0.07×10-8. 儿童ADDing的最大值为0.66×10-6、最小值为0.06×10-6和均值为0.14×10-6;儿童ADDinh的最大值为0.18×10-16、最小值为0.01×10-16和均值为0.03×10-16;儿童ADDdermal的最大值为0.18×10-8、最小值为0.01×10-8和均值为0.04×10-8. 以上结果说明, 暴露途径决定着土壤Cd元素健康风险程度的高低. 研究区手-口摄入是土壤Cd元素引起健康风险的主要途径, 皮肤暴露造成的健康风险相对较小, 经呼吸途径引起的健康风险极小, 可以忽略不计.
通过对CR指数的分析可知, 成人CR指数介于0.24~2.72之间, 均值为0.59;儿童CR指数介于0.39~4.31之间, 均值为0.92. 说明因成人与儿童的行为和生理特征存在明显差异, 儿童比成人对土壤环境中的Cd元素更加敏感, 需注意加强儿童的健康风险防范. 值得注意的是, 研究区所有样本的CR系数均小于10-4, 处于美国环境保护署(USEPA)规定的可接受致癌风险等级, 说明研究区土壤Cd元素对人体没有明显的致癌影响.
3.2 土壤Cd元素健康风险预测以TP、TN、SOC、TL、NDVI、pH和ST为最佳辅助变量分别建立了LR、BP、SVM、RF和RBF共5种土壤Cd元素健康风险评价模型. 分成人、儿童两类人群, 随机选取70%的数据开展模型训练工作, 同时以30%的辅助变量数据集作为输入变量进行模型验证, 获得验证点的土壤Cd元素健康风险评价预测值, 对比预测值与实测值, 获取不同模型的拟合优度参数、预测精度参数(表 4).
|
|
表 4 不同模型对不同人群的土壤镉元素健康风险预测精度 Table 4 Accuracy of different models in predicting health risk from soil cadmium in different populations |
由表 4可知, RF模型对成人与儿童的Cd元素健康风险评价的预测精度优于其他4种模型, 其对成人致癌风险预测的R2值为0.705 6, 对儿童致癌风险预测的R2为0.734 2, 预测效果最佳;其次为SVM模型, 预测精度较高, 对成人致癌风险的R2值为0.671 2, 对儿童致癌风险的R2值为0.653 4, 预测结果相对较好;LR模型对成人致癌风险预测的R2值为0.482 7, 对儿童致癌风险预测的R2为0.507 3, 预测精度最低.
4 讨论对于土壤重金属元素的空间分布预测, 不同机器学习模型的学习性能存在明显差异[39]. 在本研究中, 相比于非线性模型(RF、SVM、BP、RBF), 线性模型(LR)对土壤重金属的空间预测精度整体偏低, 原因可能是其只能捕捉变量之间的线性关系, 侧重对重点变量的系数估计的准确性, 对于变量遗漏的内生性问题无法直接检验, 导致模型的预测效果受限[40]. Tan等[41]的研究不仅证实了线性模型的可靠性, 同时也提出了线性模型存在的具体缺陷, 说明了非线性模型相比单纯线性模型的优势.
在4种非线性模型中, RF模型具有较高R2值和较低的RMSE、MAE和MBE值, 是研究区土壤Cd含量和健康风险预测的最优模型. Li等[42]、林小兵等[43]和许洋等[16]对广东、江西和浙江等地农田土壤中Cd元素空间分布的预测过程中, RF模型均表现出良好的预测效果. 金昭等[12]对比了MLR、ENR、RF、SGB和Stacking集成模型、BP神经网络、avNNet、SVM-L及SVM-R共9种经典机器学习模型对土壤重金属的空间预测精度, 发现RF的预测结果更加精确;其原因可能是RF模型具有较好的泛化能力, 同时其引入了随机性原则, 降低了过拟合几率[44]. 同时本文结果证实, SVM模型的预测性能仅次于RF模型, 在对土壤Cd含量及健康风险预测中也取得了较高的R2和较低的RMSE、MAE、MBE值. Sakizadeh等[35]研究发现, 高斯核是SVM建模过程中最常用的核函数, 该研究对比了基于线性核、高斯核和多项式核这3种核函数的SVM对土壤重金属空间预测的精度, 发现采用高斯核的SVM具有更高的精确性.
5 结论(1)研究区ω(Cd)均值为0.14 mg·kg-1, 是新疆土壤背景值的1.17倍. Hg等其他重金属元素的均值未超过其背景值, 说明研究区土壤中Cd元素较为富集, 是区内土壤重金属污染的主要因子. 通过对致癌风险系数CR的分析可知, 成人CR指数均值为0.59;儿童CR指数均值为0.92, 说明儿童比成人对土壤环境中的Cd元素更加敏感;所有样本的CR值均低于USEPA规定的阈值, 说明研究区不存在长期健康风险影响.
(2)5种机器学习模型中, RF模型验证集R2值为0.763 7, 在5种模型中最大;RMSE、MAE和MBE值分别为0.018 0、0.013 7和4.65e-4, 在5种模型中最小, 说明土壤中Cd元素含量真实值与RF模型的预测值拟合效果最佳. 同时, 在土壤Cd元素健康风险预测中, RF模型在成人与儿童的土壤Cd元素健康风险评价的反演精度均优于其他4种模型, 其中RF模型验证集的R2为0.705 6, 对儿童的R2为0.734 2.
(3)在5种机器学习模型中, RF模型是研究区土壤Cd含量预测和健康风险评价的最优模型, 因为其具有较好的泛化能力和抗过拟合能力;SVM模型的预测性能仅次于RF模型, 高斯核是SVM建模过程中最常用的核函数, 因为其具有更高的精确性;LR模型因为仅能构建变量之间简单的线性关系, 导致模型的预测受到限制.
| [1] | Yang X L, Cheng J, Franks A E, et al. Loss of microbial diversity weakens specific soil functions, but increases soil ecosystem stability[J]. Soil Biology and Biochemistry, 2023, 177. DOI:10.1016/j.soilbio.2022.108916 |
| [2] |
朱永官, 李刚, 张甘霖, 等. 土壤安全: 从地球关键带到生态系统服务[J]. 地理学报, 2015, 70(12): 1859-1869. Zhu Y G, Li G, Zhang G L, et al. Soil security: from Earth's critical zone to ecosystem services[J]. Acta Geographica Sinica, 2015, 70(12): 1859-1869. DOI:10.11821/dlxb201512001 |
| [3] | Zhang Y X, Song B, Zhou Z Y. Pollution assessment and source apportionment of heavy metals in soil from lead-Zinc mining areas of south China[J]. Journal of Environmental Chemical Engineering, 2023, 11(2). DOI:10.1016/j.jece.2023.109320 |
| [4] | Huang Y, Wang L Y, Wang W J, et al. Current status of agricultural soil pollution by heavy metals in China: a meta-analysis[J]. Science of the Total Environment, 2019, 651(P2): 3034-3042. |
| [5] |
梁家辉, 田亦琦, 费杨, 等. 华北典型工矿城镇土壤重金属来源解析及潜在生态风险评价[J]. 环境科学, 2023, 44(10): 5657-5665. Liang J H, Tian Y Q, Fei Y, et al. Source apportionment and potential ecological risk assessment of soil heavy metals in typical industrial and mining towns in North China[J]. Environmental Science, 2023, 44(10): 5657-5665. |
| [6] | Conoscenti C, Sheshukov A Y. Regional variability of terrain index and machine learning model applications for prediction of ephemeral gullies[J]. Geomorphology, 2023, 442. DOI:10.1016/J.GEOMORPH.2023.108915 |
| [7] | Huang Y Y, Molavi Nojumi M, Ansari S, et al. Evaluating the use of machine learning for moisture content prediction in base and subgrade layers[J]. Road Materials and Pavement Design, 2023, 24(12): 2910-2928. DOI:10.1080/14680629.2023.2182135 |
| [8] | Sridevy S, Raj M N, Kumaresan P, et al. Mapping of soil properties using machine learning techniques[J]. International Journal of Environment and Climate Change, 2023, 13(8): 684-700. DOI:10.9734/ijecc/2023/v13i81997 |
| [9] |
张育福, 潘哲祺, 陈丁江. 基于机器学习的长江流域农田氮径流流失负荷估算[J]. 环境科学, 2023, 44(7): 3913-3922. Zhang Y F, Pan Z Q, Chen D J. Estimation of cropland nitrogen runoff loss loads in the Yangtze River Basin based on the machine learning approaches[J]. Environmental Science, 2023, 44(7): 3913-3922. |
| [10] | Zhang P, Yin Z Y, Jin Y F. State-of-the-art review of machine learning applications in constitutive modeling of soils[J]. Archives of Computational Methods in Engineering, 2021, 28(5): 3661-3686. DOI:10.1007/s11831-020-09524-z |
| [11] |
牛硕, 李艳玲, 杨阳, 等. 基于机器学习方法的小麦镉富集因子预测[J]. 环境科学, 2023, 44(6): 3619-3626. Niu S, Li Y L, Yang Y, et al. Prediction of cadmium uptake factor in wheat based on machine learning[J]. Environmental Science, 2023, 44(6): 3619-3626. |
| [12] |
金昭, 吕建树. 基于机器学习模型的区域土壤重金属空间预测精度比较研究[J]. 地理研究, 2022, 41(6): 1731-1747. Jin Z, Lü J S. Comparison of the accuracy of spatial prediction for heavy metals in regional soils based on machine learning models[J]. Geographical Research, 2022, 41(6): 1731-1747. |
| [13] |
刘烨坤, 郝晓剑, 杨彦伟, 等. 腔体约束LIBS结合机器学习对土壤重金属元素的定量分析[J]. 光谱学与光谱分析, 2022, 42(8): 2387-2391. Liu Y K, Hao X J, Yang Y W, et al. Quantitative analysis of soil heavy metal elements based on cavity confinement LIBS combined with machine learning[J]. Spectroscopy and Spectral Analysis, 2022, 42(8): 2387-2391. |
| [14] | Guan Q Y, Zhao R, Wang F F, et al. Prediction of heavy metals in soils of an arid area based on multi-spectral data[J]. Journal of Environmental Management, 2019, 243: 137-143. |
| [15] | Sergeev A P, Buevich A G, Baglaeva E M, et al. Combining spatial autocorrelation with machine learning increases prediction accuracy of soil heavy metals[J]. CATENA, 2019, 174: 425-435. DOI:10.1016/j.catena.2018.11.037 |
| [16] |
许洋, 陈健松, 王志栋, 等. 基于多源异构数据的典型场地土壤重金属污染模拟预测研究[J]. 环境科学学报, 2023, 43(9): 357-368. Xu Y, Chen J S, Wang Z D, et al. Simulation and prediction research of heavy metal pollution in soil of typical sites based on multi-source heterogeneous data[J]. Acta Scientiae Circumstantiae, 2023, 43(9): 357-368. |
| [17] |
黄煜韬, 施维林, 纪娟, 等. 基于BP神经网络对某电镀厂土壤重金属预测及人体健康风险评价[J]. 生态毒理学报, 2022, 17(2): 278-289. Huang Y T, Shi W L, Ji J, et al. Prediction of soil heavy metals based on BP neural network and assessment of human health risk of an electroplating plant[J]. Asian Journal of Ecotoxicology, 2022, 17(2): 278-289. |
| [18] |
任加国, 龚克, 马福俊, 等. 基于BP神经网络的污染场地土壤重金属和PAHs含量预测[J]. 环境科学研究, 2021, 34(9): 2237-2247. Ren J G, Gong K, Ma F J, et al. Prediction of heavy metal and PAHs content in polluted soil based on BP neural network[J]. Research of Environmental Sciences, 2021, 34(9): 2237-2247. |
| [19] | Chen Y, Liu Z Y, Xu C X, et al. Heavy metal content prediction based on random forest and sparrow search algorithm[J]. Journal of Chemometrics, 2022, 36(10). DOI:10.1002/CEM.3445 |
| [20] |
王春帅, 姚立伟, 刘弋珲, 等. GWR模型下农用地土壤镍空间分布预测[J]. 遥感信息, 2021, 36(1): 43-49. Wang C S, Yao L W, Liu Y H, et al. Prediction of soil nickel spatial distribution in agricultural soil under GWR model[J]. Remote Sensing Information, 2021, 36(1): 43-49. |
| [21] | Sulieman M M, Kaya F, Keshavarzi A, et al. Spatial variability of some heavy metals in arid harrats soils: combining machine learning algorithms and synthetic indexes based-multitemporal Landsat 8/9 to establish background levels[J]. CATENA, 2024, 234. DOI:10.1016/J.CATENA.2023.107579 |
| [22] | Wang X, Yu D S, Ma L X, et al. Using big data searching and machine learning to predict human health risk probability from pesticide site soils in China[J]. Journal of Environmental Management, 2022, 320. DOI:10.1016/J.JENVMAN.2022.115798 |
| [23] |
杨煜岑, 杨联安, 王晶, 等. 基于多元线性回归模型的土壤养分空间预测——以陕西省蓝田县农耕区为例[J]. 土壤通报, 2017, 48(5): 1102-1113. Yang Y C, Yang L A, Wang J, et al. Prediction of spatial distribution of soil nutrients based on multiple linear regression model——a case study in Lantian county of Shaanxi Province[J]. Chinese Journal of Soil Science, 2017, 48(5): 1102-1113. |
| [24] | John K, Bouslihim Y, Bouasria A, et al. Assessing the impact of sampling strategy in random forest-based predicting of soil nutrients: a study case from northern Morocco[J]. Geocarto International, 2022, 37(26): 11209-11222. DOI:10.1080/10106049.2022.2048091 |
| [25] | Zhang X S, He B, Sabri M M S, et al. Soil liquefaction prediction based on Bayesian optimization and support vector machines[J]. Sustainability, 2022, 14(19). DOI:10.3390/su141911944 |
| [26] | Tao L L, Wang G J, Chen X, et al. Soil moisture retrieval using modified particle swarm optimization and back-propagation neural network[J]. Photogrammetric Engineering & Remote Sensing, 2019, 85(11): 789-798. |
| [27] |
李启权, 王昌全, 岳天祥, 等. 基于RBF神经网络的土壤有机质空间变异研究方法[J]. 农业工程学报, 2010, 26(1): 87-93. Li Q Q, Wang C Q, Yue T X, et al. Method for spatial variety of soil organic matter based on radial basis function neural network[J]. Transactions of the Chinese Society of Agricultural Engineering, 2010, 26(1): 87-93. |
| [28] |
郭志娟, 刘飞, 周亚龙, 等. 雄安新区土壤氟地球化学特征及健康风险评价[J]. 环境科学, 2023, 44(8): 4397-4405. Guo Z J, Liu F, Zhou Y L, et al. Potential ecological risk assessment and source analysis of heavy metals in soil-crop system in Xiong'an new district[J]. Environmental Science, 2023, 44(8): 4397-4405. |
| [29] |
陈景辉, 郭毅, 杨博, 等. 省会城市土壤重金属污染水平与健康风险评价[J]. 生态环境学报, 2022, 31(10): 2058-2069. Chen J H, Guo Y, Yang B, et al. Pollution level of heavy metals in soil and health risk assessment in provincial capital cities of China[J]. Ecology and Environment Sciences, 2022, 31(10): 2058-2069. |
| [30] |
阿吉古丽·马木提, 麦麦提吐尔逊·艾则孜, 艾尼瓦尔·买买提, 等. 开都河下游绿洲耕地土壤重金属污染及潜在生态风险[J]. 环境科学学报, 2017, 37(6): 2331-2341. Mamut A, Eziz M, Mohammad A, et al. Heavy metal pollution and potential ecological risks of farmland soils in oasis along the lower reaches of Kaidu River[J]. Acta Scientiae Circumstantiae, 2017, 37(6): 2331-2341. |
| [31] |
布买日也木·买买提. 环塔里木盆地绿洲城市空间过程与重心转移特征[D]. 乌鲁木齐: 新疆大学, 2017. Bubaizhiyimu M. Characteristics of spatial process and centre of gravity shift in oasis cities around Tarim Basin [D]. Urumqi: Xinjiang University, 2017. |
| [32] | Yang H R, Huang K, Zhang K, et al. Predicting heavy metal adsorption on soil with machine learning and mapping global distribution of soil adsorption capacities[J]. Environmental Science & Technology, 2021, 55(20): 14316-14328. |
| [33] |
苏志强. 基于机器学习和极化特征优选的干旱区土壤水分雷达遥感研究[D]. 西安: 长安大学, 2021. Su Z Q. Radar remote sensing research on soil moisture in arid areas using machine learning and polarization feature optimization[D]. Xi'an: Chang'an University, 2021. |
| [34] |
韩文霆, 崔家伟, 崔欣, 等. 基于特征优选与机器学习的农田土壤含盐量估算研究[J]. 农业机械学报, 2023, 54(3): 328-337. Han W T, Cui J W, Cui X, et al. Estimation of farmland soil salinity content based on feature optimization and machine learning algorithms[J]. Transactions of the Chinese Society for Agricultural Machinery, 2023, 54(3): 328-337. |
| [35] | Sakizadeh M, Mirzaei R, Ghorbani H. Support vector machine and artificial neural network to model soil pollution: a case study in Semnan Province, Iran[J]. Neural Computing and Applications, 2017, 28(11): 3229-3238. |
| [36] | Zhang P, Mei S H, Shi C C, et al. Forecasting DO of the river-type reservoirs using input variable selection and machine learning techniques-taking Shuikou reservoir in the Minjiang River as an example[J]. Ecological Indicators, 2023, 155. DOI:10.1016/J.ECOLIND.2023.110995 |
| [37] | Molla A, Zhang W W, Zou S D, et al. A machine learning and geostatistical hybrid method to improve spatial prediction accuracy of soil potentially toxic elements[J]. Stochastic Environmental Research and Risk Assessment, 2023, 37(2): 681-696. |
| [38] |
马杰, 佘泽蕾, 王胜蓝, 等. 重庆市煤矸山周边农产品镉健康风险评价及土壤环境基准值推导[J]. 环境科学, 2023, 44(9): 5264-5274. Ma J, She Z L, Wang S L, et al. Health risk assessment and environmental benchmark of cadmium in farmland soils around the gangue heap of coal mine, Chongqing[J]. Environmental Science, 2023, 44(9): 5264-5274. |
| [39] |
孙越琦. 常用机器学习模型在土壤属性空间预测与数字化制图中性能表现对比研究[D]. 郑州: 郑州大学, 2022. Sun Y Q. Performance of machine learning algorithm in soil property spatial prediction and digital soil mapping[D]. Zhengzhou: Zhengzhou University, 2022. |
| [40] | Makungwe M, Chabala L M, Chishala B H, et al. Performance of linear mixed models and random forests for spatial prediction of soil pH[J]. Geoderma, 2021, 397. DOI:10.1016/J.GEODERMA.2021.115079 |
| [41] | Tan K, Ma W B, Wu F Y, et al. Random forest-based estimation of heavy metal concentration in agricultural soils with hyperspectral sensor data[J]. Environmental Monitoring and Assessment, 2019, 191(7). DOI:10.1007/s10661-019-7510-4 |
| [42] | Li X Y, Geng T, Shen W J, et al. Quantifying the influencing factors and multi-factor interactions affecting cadmium accumulation in limestone-derived agricultural soil using random forest (RF) approach[J]. Ecotoxicology and Environmental Safety, 2021, 209. DOI:10.1016/j.ecoenv.2020.111773 |
| [43] |
林小兵, 武琳, 王惠明, 等. 基于农田土壤镉污染修复后糙米镉的指标筛选[J]. 土壤通报, 2021, 52(1): 203-210. Lin X B, Wu L, Wang H M, et al. Screening of indicators in brown rice cadmium after remediation of cadmium pollution in farmland soil[J]. Chinese Journal of Soil Science, 2021, 52(1): 203-210. |
| [44] | Gambill D R, Wall W A, Fulton A J, et al. Predicting USCS soil classification from soil property variables using Random Forest[J]. Journal of Terramechanics, 2016, 65: 85-92. |
 2024, Vol. 45
2024, Vol. 45


