随着全球范围内对环境保护和气候变化问题的深度关注, 二氧化碳排放已经被公认为是加剧全球气候变化的重要因素之一. 其中, 交通运输业的二氧化碳排放问题受到了特别的关注. 在全球范围内, 交通运输行业的二氧化碳排放占全球总排放量的大约23%, 并且这一比例仍在持续上升. 在中国, 由于经济的快速发展和城市化进程的加快, 交通运输业的规模和贡献度逐年增加, 但其也在不断地给环境带来巨大的负面影响, 其中之一就是CO2的排放[1]. 交通运输业是仅次于工业、建筑业的第三大排放源[2], 其排放量占中国总排放量的比例持续上升, 对气候变化和环境污染产生了深远影响. 并且, 由于城市化进程和社会经济发展的需求, 中国的交通运输业在可预见的未来还将继续快速发展, 这使得如何有效控制和降低交通运输业的二氧化碳排放成为了一个迫切需要解决的问题.
为了控制交通运输二氧化碳排放, 需要深入了解交通运输排放的模式和趋势, 建立科学的预测模型, 为政策制定提供依据和决策支持. 国内外学者对交通运输CO2预测工作进行了大量研究[3~6], 预测方法主要包括基于统计学的预测方法和基于物理模型的预测方法. 基于统计学的交通碳排放预测模型主要是基于历史数据的统计分析和建模, 利用时间序列分析[7]、回归分析[8]和主成分分析[9]等方法对交通碳排放量进行预测. 常见的预测模型包括ARIMA模型[10]、VAR模型[11]、Lasso回归模型[12]和岭回归模型[13]等. 基于物理模型的交通碳排放预测方法是通过建立交通运输系统的物理模型, 分析交通系统中各种因素的作用和交互关系, 从而预测交通碳排放量的方法. 以上模型通常基于交通运输系统的能量流动和物质流动原理, 涉及交通运输系统中的车辆、路网、交通流和车辆燃料消耗等多个方面, 需要较为精细的建模和数据支撑, 常见的模型有MOVES模型[14]和COPERT[15]等. 以上模型在不同的应用场景中都有着广泛的应用, 通常具有较高的精度和可靠性, 然而, 基于统计学的预测方法需要大量历史数据, 对新情况的预测能力较弱. 基于物理模型的预测方法也需要大量的基础数据和专业知识, 建模难度较大, 成本较高, 且需要较为专业的技术支持.
近年来, 为弥补数值模型的不足, 学者们逐渐将机器学习方法应用到交通运输CO2预测中. 常见的机器学习方法包括深度学习(DL)[16, 17]、支持向量机(SVM)[18~20]、决策树(DT)[21]、随机森林(RF)[22~25]、极限梯度提升(XGBoost)[26~29]、人工神经网络(ANN)[30, 31]和K近邻算法(KNN)[32]. Ağbulut [33]使用多种机器学习算法预测土耳其与运输相关的能源需求和CO2排放, 发现SVM、ANN和DL算法都取得了理想结果, 其中SVM表现最优. Li等[34]使用30个国家的数据, 基于普通最小二乘回归、SVM和XGBoost算法, 预测全球层面的交通运输的CO2排放, 发现XGBoost算法表现最优. 李文翔等[15]基于历史的合乘行程碳减排及其订单特征数据, 训练XGBoost模型以预测未来潜在合乘出行的碳减排状态, 发现XGBoost模型可以有效预测网约车合乘出行的碳减排状态. 高金贺等[35]以北京1995~2016年交通运输相关数据, 分别将遗传优化算法、粒子群优化算法、网格搜索算法与支持向量机结合, 构建用于预测城市交通碳排放模型, 结果显示模型具有良好的学习和推广能力.
以上研究表明, 机器学习方法在交通运输CO2预测方面具有良好的应用前景. 然而目前大多是针对单一地区和单一机器学习算法预测交通运输碳排放研究, 对于多区域的研究大多是没有考虑区域差异性. 本文以中国30个省份(中国香港、澳门、台湾和西藏资料暂缺)2005~2019年面板数据为数据集, 从国家层面, 考虑省份差异性, 基于不同机器学习算法构建交通运输CO2预测模型, 比较分析各模型的预测效果和准确性, 找出最优的预测方法, 实现对交通运输CO2的准确预测, 对交通运输二氧化碳排放量的预测提供了一种新的思路和方法, 并且对于政府和相关机构制定交通运输节能减排政策和管理措施具有重要的实践意义.
1 材料与方法 1.1 交通二氧化碳排放量影响因素选取交通运输碳排放受到各种不同领域影响因素的干扰, 通过对已有研究的梳理, 如表 1所示, 将影响交通碳排放的因素分为内因和外因. 将交通运输业本身对碳排放量的影响归为内因, 如客、货周转量的增加, 导致交通碳排放量增加, 技术的进步提高了交通工具的能源利用率, 从而减少碳排放量;将经济发展、社会发展等对交通碳排放量的影响归为外因, 如城市化的发展会导致产业结构的调整和升级, 以及出行结构调整和出行距离的增加, 将会影响交通碳排放量.
|
|
表 1 交通CO2排放量影响因素梳理 Table 1 Sorting out factors influencing traffic CO2 emissions |
基于数据能够获取的原则, 本文拟从外因和内因两方面出发, 内因初步选取交通基础设施密度(TFP)、城市桥梁数量(BD)、客运周转量(TN)及货运周转量(GN)表示, 外因初步选取常住人口(UP)、城镇化率(U)、第三产业占比(TR)、公共交通数量(CC)、私家车数量(PC)和城市绿地面积(GAS)来表征社会发展因素, 选取地区生产总值(GDP)、交通运输业产值(TRP)和社会商品零售总额(SSG)来表征经济发展因素, 选取交通运输结构(TS)、交通运输强度(TI)、能源强度(EI)和能源结构(ES)来表征技术发展因素, 以上因素作为交通运输碳排放(Emission)的解释变量. 考虑到不同省份本身的差异性会使得不同地区之间交通运输CO2差异很大, 因此本文将省份(Pro)也考虑进去, 作为解释变量. 其中, 交通基础设施密度用公共交通运营线路总长度(km)与城市建设用地面积(km2)的比值来表征, 交通运输结构用公路换算周转量(104 kg·km)占总的换算周转量的比重来表征, 其中公路、水路、铁路与民航的换算系数分别为0.1、0.33、1和0.072[36], 交通运输强度以交通运输周转量(104 kg·km)与地区生产总值(亿元)的比值来表征, 能源强度(t·万元-1, 以标准煤计)用交通运输业能源消耗量与交通运输业增加值的比值来表征.
1.2 数据来源本文的数据集为2005~2019年中国省域面板数据, 其中, 能源数据来源于《中国能源统计年鉴》(2005~2019年), 人口数据来源于《中国人口统计年鉴》(2005~2019年), 其他解释变量数据来源于《中国统计年鉴》(2005~2019年)和《交通运输统计公告》, 被解释变量数据来源于2005~2019年中国碳排放核算数据库(CEADs)[40], 该数据库致力于研究中国碳排放核算方法和应用, 提供了较为准确和最新的碳排放数据. 目前在《中国能源统计年鉴》(2005~2019年)、《中国统计年鉴》(2005~2019年)以及CEADs中并未对交通运输的能源消费数据予以单独统计, 而是将交通运输、仓储和邮电通信业合并统计, 由于后两者所占的比例相对较小[36], 因此本文将合并统计的数据作为交通运输业的相关数据进行研究. 本文所采用的数据集共450条数据, 将2005~2018年共420条数据, 按照85%和15%分为训练集和测试集, 将2019年的数据作为预测集, 共30条数据.
1.3 数据预处理模型训练前, 对原始数据主要进行缺失值处理与归一化处理. 缺失值处理的方法主要是删除缺失值所在行或填补缺失值, 考虑到本文缺失值比例较少且本身数据集规模不大, 因此本文使用中位数填补缺失值. 常见归一化方法有Min-Max归一化、Z-score标准化和Sigmoid归一化等. 本文使用Min-Max归一化方法将原始数据缩放到[0, 1]区间内, 其函数表达式如公式(1)所示:
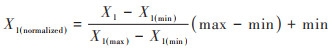
|
(1) |
式中, X1(normalized)为归化后的样本数据, X1为样本原始数据, X1(max)为样本数据最大值, X1(min)为样本数据最小值, max和min表示归一化后的最大值与最小值, 一般取max为1, min为0, 本文取max为1, min为0.
此外, 文章通过固定效应模型捕获省份间的异质性. 固定效应模型是一种有力的面板数据分析工具, 它考虑到每个省份有其独特的特征, 以上特征在本研究的时间范围内不发生变化, 例如自然资源, 地理位置等. 以上固定的特征被统称为“省份差异”, 它们在省份间存在, 但在时间内保持恒定. 通过给每个省份添加一个固定效应变量来考虑省份个体差异, 进而提高预测准确度. 个体固定效应系数的计算表达式如公式(2)所示:
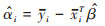
|
(2) |
式中, 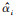
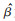
本文初步选取的解释变量较多, 且不同变量对交通运输碳排放量的影响不同, 某些变量可能与最终预测结果相关性很低, 因此在对交通运输碳排放进行预测时, 首先需要对18个解释变量进行筛选和分析, 从而提高最终预测的准确性. 在计算18个解释变量与交通运输碳排放之间的相关性系数时, 通常使用Pearson相关系数法, 该系数是一种用于衡量两个变量之间线性关系的度量. 然而计算Pearson相关系数时默认假设两者之间存在线性关系, 当两个变量之间存在很强但非线性的关系时, 它将无法识别[41]. 考虑到各解释变量与交通运输碳排放之间关系复杂, 并非都是线性关系, Pearson相关系数可能不是最合适的度量方式. 因此, 本文使用Spearman秩相关系数来度量18个解释变量与交通运输碳排放之间的关系以及18个解释变量之间相关性. Spearman秩相关系数的计算公式如下:
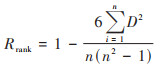
|
(3) |
式中, D为每对数据之间秩的差值, n表示样本数据.
1.4.2 变量重要性计算计算变量重要性有助于选择最优的特征组合和调整模型参数, 通常对于不同的机器算法, 其重要性计算的方法不同, 本文选择SHAP值来计算解释变量的重要性, SHAP值的计算方法基于博弈论, 能够精确地计算每个特征对于模型输出的贡献, 以及样本之间的相互作用, 因此可以更加准确地评估特征的重要性. 本文SHAP值的计算通过PYTHON软件中的SHAP库实现.
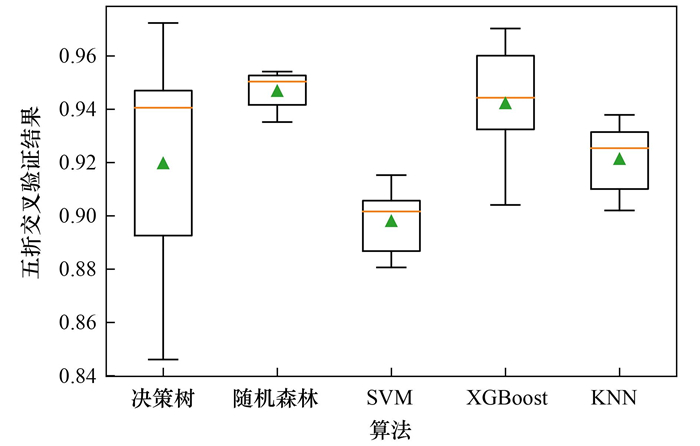
1.4.3 算法选择通过文献回顾, 对于回归预测问题常用的机器学习算法主要有决策树算法、随机森林算法、支持向量机算法(SVM)、线性回归法、神经网络算法、极端梯度提升算法(XGBoost)和K近邻算法(KNN), 不同的数据集适合于不同的算法. 考虑到本文的解释变量较多, 与交通运输碳排放可能并不都是线性关系, 因此线性回归法不适合本文的数据集. 此外, 由于本文数据集规模不大, 使用神经网络算法容易过拟合, 本文在剩余5种算法中进行初步筛选, 通过五折交叉验证, 以R2结果作为评价标准, 选出适合本数据集的算法. 图 1展示了5种机器学习算法对本数据集的适应性, 从中可以看出决策树得出的结果稳定性最差, SVM得出的结果准确性最差, 综合来看, 随机森林算法、XGBoost算法以及KNN算法更适合于本文的数据集, 其中随机森林算法在数据集上表现最好, 因此本文采用随机森林算法、XGBoost算法和KNN算法分别构建交通运输碳排放预测模型:Model_rf、Model_xg和Model_knn.
|
橙色线表示中位线, 三角表示每组结果的均值, 箱体的长度表示结果的稳定性 图 1 不同机器学习算法五折交叉验证结果 Fig. 1 Five-fold cross-validation results of different machine learning algorithms |
随机森林算法最早由BREIMAN提出, 通过构建多棵决策树并取其平均结果以防止过拟合[42], 本研究从原始训练集中随机选择85%的样本构成训练子集, 使用自助采样(bootstrap sampling)方法进行选择. 剩余的15%被用作袋外(out-of-bag)数据, 用于模型的验证和性能评估. 对于每一个训练子集, 构建一个决策树, 每一次节点分裂时, 本研究从所有的特征中随机选择一部分特征, 本文选择最小化均方误差MSE来选择最佳的分裂特征和分裂点, 节点分裂的公式由公式(4)表示:
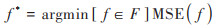
|
(4) |
式中, f *为在F中使MSE最小的特征, argmin为求使函数取最小值时的变量. F为一组特征或者变量, 在随机森林中, 每次分裂节点时, 会从所有特征中随机选择一部分特征形成这个F. 本文预测模型的构建是通过PYTHON的机器学习库Scikit-Learn实现的. 文章选择使用网格搜索算法对模型参数进行优化, 优化后得到模型的树的数目为100, 特征数为11, 树的最大深度为10.
XGBoost是一个隶属于集成学习模型的Boosting算法[43], 核心思想是对一系列弱模型(通常是决策树)的预测结果进行加权组合. 本文XGBoost算法的目标函数为损失函数和正则化项之和, 由公式(5)~(7)表示:
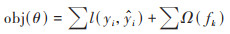
|
(5) |
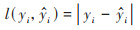
|
(6) |
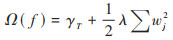
|
(7) |
式中, l(yi, 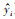
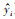
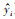
模型的学习过程, XGBoost采用梯度提升方法, 对于每一步, 它都会添加一个新的树ft, 来最小化目标函数. 添加的这棵树会使得损失函数下降最快. 新树的添加形式由公式(8)表示:
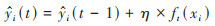
|
(8) |
式中, η为学习率, 控制每一步的更新幅度, xi为第i个样本的特征向量. 值得注意的是, fk和ft都指模型中的一棵树. fk为模型中的第k棵树, 而 ft为在梯度提升的第t步, 添加到模型中的新树. 本文预测模型的构建是通过Python的机器学习库Scikit-Learn和XGBoost实现的. 文章选择使用网格搜索算法对模型参数进行优化, 优化后得到模型的树的数目为200, 特征数为11, 树的最大深度为5, 学习率为0.1.
KNN算法的基本思想是利用距离公式表征两两样本间的距离, 提取样本中距离最小的K个点作为预测参考值[44], 通过找到最近的K个观测值, 然后投票决定预测结果. 本文首先使用欧氏距离公式来计算两个样本之间的距离, 如公式(9)所示, 以此在训练集中找到最近邻的K个样本.
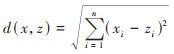
|
(9) |
式中, x和z为两个样本, n为特征数量, xi和zi为x和z的第i个特征. 直接计算这K个最近邻样本的目标值的平均值作为预测结果, 如公式(10)所示:
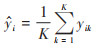
|
(10) |
式中, K为邻居的数量, yik为第k个邻居的目标值, 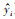
模型测试有助于评估模型的性能和准确性, 找出模型的优缺点, 指导模型改进和优化, 从而提高模型的预测能力和泛化能力. 本文从泛化能力以及是否过拟合或欠拟合两个方面对模型进行测试与分析. 交叉验证(cross-validation)[45]是一种常用的机器学习模型泛化能力测试方法, 本文采用K折交叉验证方法, 将数据集分成k份, 每次将其中一份作为测试集, 其余k - 1份作为训练集, 重复k次, 最后将k次的评估指标取平均值作为构建的交通运输碳排放预测模型的性能指标. 学习曲线的方法可以绘制出训练误差和测试误差随着数据集大小的变化而变化的曲线, 是机器学习中测试模型是否过拟合或欠拟合的常用方法. 如果训练误差和测试误差之间的差距很大, 那么就可能存在过拟合或欠拟合的问题. 如果训练误差和测试误差之间的差距很小, 并且随着数据集大小的增加而逐渐收敛, 则说明模型具有良好的拟合能力. 总体而言, 进行交叉验证和绘制学习曲线是互补的步骤, 两者都是评估模型性能的重要手段.
1.5.2 评价指标本文选用文献中使用最多的4种不同的度量标准来评价Model_rf、Model_xg和Model_knn性能的成功性. 分别为均方误差(MSE)、平均绝对误差(MAE)、决定系数(R2)和平均绝对百分比误差(MAPE).
2 结果与讨论 2.1 变量相关性分析为定量分析18个解释变量与交通运输碳排放的关系, 本文基于数据集(共450条数据), 首先计算出各省份(Pro)的个体固定效应系数, 然后选用Spearman秩相关系数法计算18个解释变量与交通运输碳排放之间的相关性系数, 并结合显著性检验的方法对解释变量进行筛选, 相关性系数及排名如图 2所示.
|
**表示在0.01水平(双侧)上显著相关 图 2 18个解释变量与被解释变量之间的相关性 Fig. 2 Correlation of explanatory variables with the explained variables |
初步选取的解释变量中有11个变量通过0.01双侧显著性检验, 说明与被解释变量具有强相关性. 其中省份与交通运输碳排放相关性最高, 为0.860, 原因可能是不同省份的经济水平和交通规模不同, 经济发达的省份和交通密集的省份可能会有更高的交通运输碳排放量. 此外, 一些省份的地理位置可能会导致交通运输碳排放量相对较高, 例如, 位于东部沿海的一些省份, 由于交通运输便捷和物流发达等因素, 其交通运输碳排放量可能会相对较高. 不同省份的交通管理和政策可能会影响交通运输碳排放量, 例如, 一些省份可能会采取更加严格的车辆尾气排放标准, 以降低交通运输碳排放. 其次, 公共交通数量(CC)、私家车数量(PC)、GDP和人口数量(UP)等因素相关性排名较高, 因为它们本身就与交通碳排放的产生有直接关系, 可以更直接地影响交通碳排放. 例如, 公共交通数量和私家车数量直接影响了交通工具的使用情况, 从而影响交通碳排放;GDP和人口数量则直接影响了交通需求的规模和性质, 也会影响交通碳排放.
有7个变量未通过显著性检验, 分别是交通运输强度(TI)、交通运输结构(TS)、能源结构(ES)、能源强度(EI)、城镇化率(U)、第三产业占比(TR)和客运周转量(TN), 说明与被解释变量相关性不强, 可能的原因是, 与公共交通数量(CC)、私家车数量(PC)、GDP和人口数量(UP)等因素不同, 以上因素更多地是反映交通运输系统的基本特征和特性, 与交通碳排放之间的关系比较复杂, 可能并不能直接反映交通碳排放. 因此, 以上因素与交通碳排放的相关性可能会相对较弱.
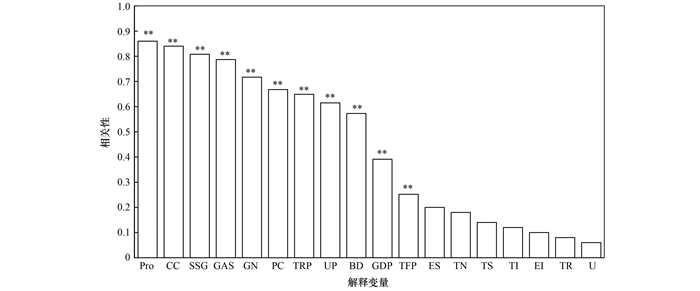
为了减少解释变量之间多重共线性带来的影响, 需要计算解释变量之间的相关性. 一般相关系数大于0.7则说明关系非常紧密, 位于0.4~0.7之间则说明关系紧密, 位于0.2~0.4之间则说明关系一般[13], 因此, 本文将阈值设为0.4, 选取与被解释变量相关性超过0.4的解释变量, 计算它们之间的相关性系数, 结果如图 3所示. 同样设置阈值为0.4, 从图 3(a)中可以看出, 公共交通数量(CC)和城市桥梁数量(BD)与其他任一变量的Spearman相关性系数都大于0.4, 认为这两个变量与其他变量关系密切, 大概率存在共线性, 不利于模型的训练, 用Pearson算法计算的线性相关性如图 3(b)所示, 验证了上述猜想. 因此, 本文最终选定Pro、SSG、GAS、GN、PC、TRP和UP这7个解释变量作为Model_rf、Model_xg和Model_knn的输入变量, 交通运输碳排放量(Emission)作为模型的输出变量, 变量统计信息如表 2所示.
|
1.UP, 2.CC, 3.PC, 4.BD, 5.GN, 6.GAS, 7.TRP, 8.SSG, 9.Pro 图 3 解释变量之间的相关性系数 Fig. 3 Correlation coefficients of explanatory variables |
|
|
表 2 变量统计信息 Table 2 Statistical information of variables |
2.2 模型测试结果
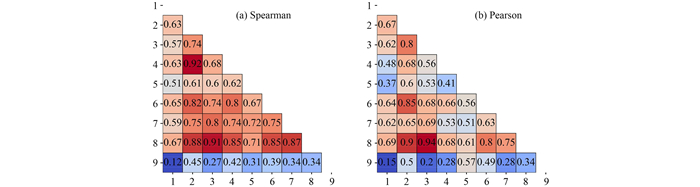
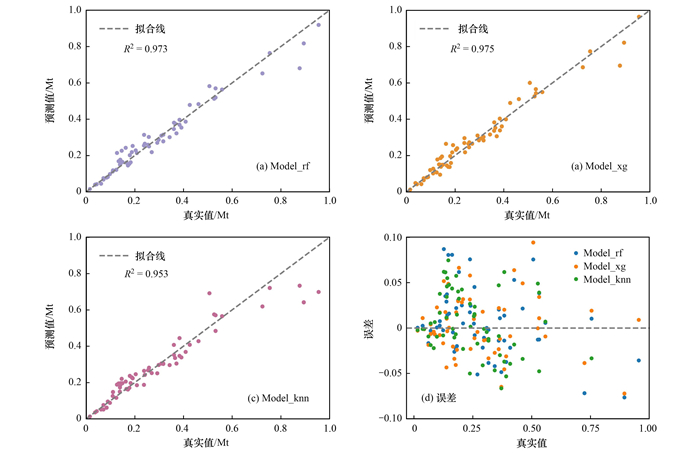
本文将数据集中在2005~2018年30个省份的面板数据, 共计420条, 按照85%和15%划分训练集和测试集, 将2019年面板数据作为预测集, 共30条, 重新输入最佳参数, 以R2作为验证指标, Model_rf、Model_xg和Model_knn在训练集和测试集上的计算结果与误差如图 4和图 5所示. 图 4(a)~4(c)和5(a)~5(c)表示的是3种模型在训练集与测试集上拟合效果, 由于对原始数据进行了归一化处理, 因此预测值与真实值的取值范围为[0, 1], 从中可以看出, 3种模型的预测值与实际值十分接近, 且3种模型在训练集上R2都大于0.97, 在测试集上R2都大于0.95, 模型的整体拟合性能较高.
|
图 4 3种模型在训练集上的预测结果及误差 Fig. 4 Prediction results and errors of the three models on the training set |
|
图 5 3种模型在测试集上的预测结果及误差 Fig. 5 Prediction results and errors of the three models on the test set |
此外, 本文在训练集与测试集进行了误差检验, 即用真实值与预测值之间的差值表示误差, 结果如图 4(d)和图 5(d)所示. 从中可以看出训练集与测试集上的误差范围都是[-0.1, 0.1], 而一般预测误差在10%以内均属于优秀预测[46], 这表明3种模型都通过了误差检验. 在训练集上, XGBoost算法的误差最小, 几乎都在[-0.01, 0.01]之间, 随机森林的误差范围要比KNN的小, 表明随机森林算法在训练集上预测的效果优于KNN. 3种算法在测试集上的预测效果相差不大, 可能是因为测试集上数据量较少造成的. 总体而言, 基于XGBoost算法构建的Model_xg在训练集和测试集中都取得了最佳效果.
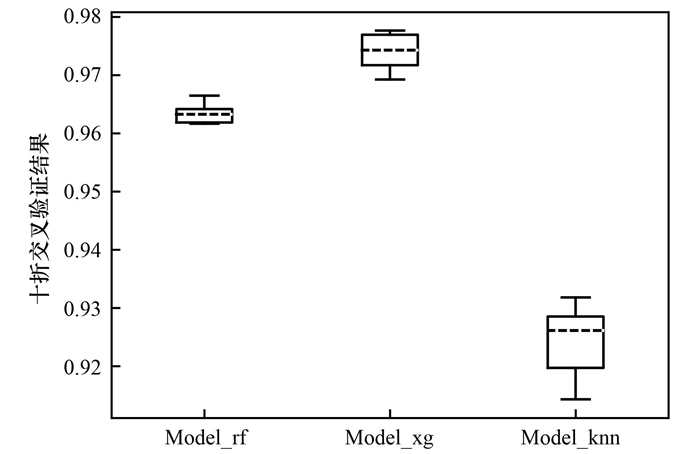
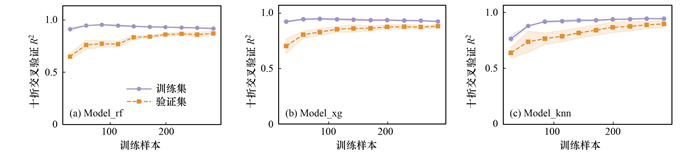
为避免过拟合问题以及随机性带来的误差, 重复多次将样本数据按照85%和15%分为训练集和测试集进行建模, 在训练集和测试集上采用十折交叉验证评估各模型性能, 用R2来表征拟合结果, 在训练集上得到的R2均值分别为0.989、0.982和0.973, 在测试集上得到的结果如图 6所示. 其中虚线代表其得分的中位线, 中位线代表十折交叉模型中的中间拟合水平, 其越高表示拟合效果越好. Model_rf和Model_xg测试集上的R2均高于0.96, 优于最初五折交叉验证的结果, 而Model_knn参数调优后, 十折交叉效果相比于前两者而言欠佳, 原因可能是模型本身稳定性不佳, 相比于前文的五折交叉验证, 十折交叉验证对模型的稳定性及准确性要求更严格. 箱体的长度从一定程度上代表模型的稳定性, 长度越短, 意味着交叉验证结果分布越密集, 模型稳定性越好. 此外, 以十折交叉验证结果R2为指标, 分别绘制3种模型在训练集与测试集上的学习曲线, 如图 7所示. 从中可以看出, 随着样本数量的增加, 3种模型训练集与测试集的R2差值逐渐减小, 随后收敛为一个值, 没有出现欠拟合与过拟合情况, 其中Model_xg的收敛值最高. 总体而言, Model_rf的模型稳定性最好, Model_xg拟合效果最优.
|
图 6 3种模型在测试集上十折交叉验证结果 Fig. 6 Ten-fold cross-validation results of the three algorithms on the test set |
|
紫色线为训练集R2随样本数量变化情况, 橙色虚线为测试集R2随样本数量变化情况, 阴影部分表示方差范围 图 7 3种模型的学习曲线 Fig. 7 Learning curve of the three models |
表 3为各模型的评估结果. MSE表示均方误差, 值越小, 表示预测结果越稳定, 根据测算结果, Model_rf与Model_xg预测的稳定性都比Model_knn好;MAE表示绝对误差, 取值是0到无穷大, 值越接近于0, 表示模型预测效果越好, 各模型的MAE取值为0.020~0.025, 其中, Model_rf取得了最理想的MAE值, Model_xg的MAE值与其相差不大;3种模型的R2值都高于0.95, 表明3种模型在预测交通运输碳排放方面都取得了理想结果, 但结合上文十折交叉验证结果来看, Model_knn预测结果的可信度不如另外两个模型;MAPE是评估预测性能的指标, 值越接近0, 表明预测性能好, 通常, MAPE ≤ 10%, 预测结果可以归类于“准确性高”, 10% < MAPE ≤ 20%, 预测结果可以归类于“准确性良好”, 20% < MAPE ≤ 50%, 预测结果可以归类于“准确性合理”, 50% < MAPE, 预测结果则归类于“不准确”[33], 从计算结果来看, Model_xg取得了最小MAPE值, 它预测的准确性较高, Model_rf和Model_knn预测的准确性良好, Model_knn的MAPE值最高, 表明它的预测性能不如另外两个模型. 综合4项指标来看, 基于XGBoost算法构建的Model_xg预测效果最好.
|
|
表 3 各模型的评估结果 Table 3 Evaluation results of each model |
综合前文分析来看, 本文认为, 针对本文所用的数据集, XGBoost算法最适合构建交通运输CO2预测模型, 并选用此模型进行后续研究分析, 随机森林算法在本数据集上的表现良好, 也适用于构建交通运输碳排放预测模型, 而KNN算法在本数据集上的表现有待提高. 进一步的, 本文基于XGBoost算法构建的模型Model_xg预测精度为0.975, 优于文献[33]构建的3种机器学习预测模型, 其预测精度为0.871~0.924, 文献[15]基于6种机器学习算法, 使用成都网约车数据构建多种预测模型, 模型预测精度为0.801~0.962, 未达到0.97. 此外, 本文的模型也优于文献[39]所构建的两种传统预测模型, 其预测精度分别为0.783~0.865与0.675~0.844. 本文通过梳理大量相关文献, 全面总结影响交通运输碳排放因素、通过多次筛选来确定最终输入变量所构建的模型, 用同一数据集可以同时预测出中国30个省份的交通运输CO2, 且预测精度高, 预测误差在可接受范围内, 比较高效且便捷.
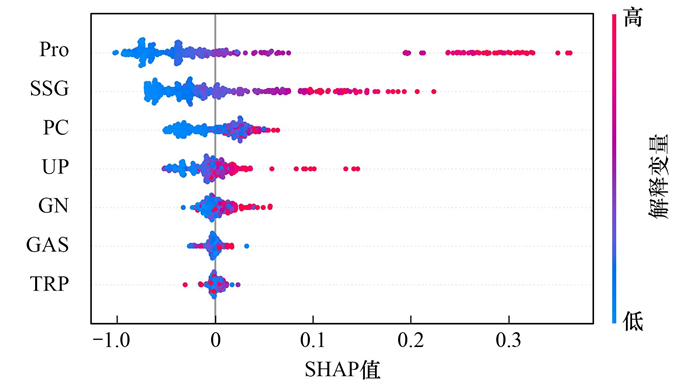
2.4 变量重要性分析7个输入变量重要性程度用SHAP值表示, 图 8为Model_xg的SHAP值, 其中, 每一个散点都表示一个样本数据.
|
解释变量从上到下的顺序表示其重要程度排名, 蓝色点表示输入变量取值较低的情况, 红色点表示取值较高的情况;SHAP值为正, 表示对交通运输碳排放量有正向影响, SHAP值为负, 表示对交通运输碳排放量有负向影响 图 8 基于Model_xg的SHAP值 Fig. 8 SHAP value based on Model_xg |
从图 8中可以看出, 省份(Pro)这一特征交通运输碳排放预测的贡献是最大的. 结合前文相关性分析可以发现, 在建立交通运输碳排放预测模型时, 考虑省份这一特征是非常重要的. 其次, 蓝色的点分布比较集中, 红色的点分布比较分散, 取值范围大, 这表明不同省份对于模型预测的影响程度是不同的. 具体而言, SHAP值为负, 表示对碳排放量产生负影响, 且值越大, 表示的是对碳排放量的影响越大, 反之则相反. 图 8中红色点几乎分布在右边, 且取值范围较大, 蓝色点几乎分布在左边, 取值范围较小, 表明Pro(用个体固定效应系数表征)与碳排放量几乎存在线性关系, 即个体固定效应系数越高, 碳排放量越高, 对碳排放量的影响程度越大, 反之则相反. 此外, 蓝色点比红色的点多, 意味着个体固定效应系数较低的省份比较多, 反映出大部分省份的交通碳排放量较低.
社会商品零售总额(SSG)在交通运输碳排放预测模型中的SHAP值排名第二, 可以看出该特征对于模型的预测结果也具有较大的影响. 通过SHAP值图, 可以发现红色点都分布在右边, 蓝色点都分布在左边且密集, 这表明社会商品消费总额和交通运输碳排放之间存在着正相关关系. 具体而言, 社会商品消费总额越高, 意味着人们的消费能力越强, 从而可能导致更多的交通运输活动, 从而增加碳排放量, 且SSG值越大, SHAP值越大, 对交通运输碳排放预测影响程度也越大. 而SSG值越小, 意味着交通运输碳排放量越少, 但是对交通运输碳排放预测影响程度不如SSG值大的时候.
私家车数量(PC)排名第三, 说明该特征对于交通运输碳排放预测的贡献也是较大的. 在该模型中, 蓝色点在左边和右边都有分布, 而红色点只分布在右边, 表明私家车数量与交通运输碳排放之间可能不是简单的线性关系. 具体而言, 私家车数量较高时, 交通运输碳排放量也较高, 而私家车数量较低时, 交通运输碳排放量也可能较低, 也可能较高, 原因可能是如果私家车数量较低, 而交通状况较为拥堵, 那么交通运输碳排放量可能仍然较高, 此外, 不同类型的车辆对于交通运输碳排放量产生的影响也是不同的, 如果私家车数量较低, 但是大部分车辆为高排放车辆, 那么交通运输碳排放量可能会较高, 且能源结构中包含较多的高碳能源, 如煤炭和石油等, 那么交通运输碳排放量可能会较高.
常住人口数量(UP)排名第四, 对交通运输碳排放的影响较为显著. 从图 8中可以看出常住人口数量对交通运输碳排放起到推动作用, 而常住人口数量较少时, 交通运输碳排放量也少, 原因可能是常住人口多意味着交通需求增加, 需要更多的交通运输工具进行运输, 从而导致交通运输碳排放量增加. 此外, 常住人口多也可能导致交通拥堵增加, 交通拥堵会导致车辆行驶速度降低, 从而使得交通运输碳排放量增加.
其他变量相对于前4名的重要程度较小, 在此不做分析. 需要注意的是, 虽然有些输入变量的影响相对较小, 但是这并不代表它不重要, 因为在多个特征同时作用下, 输入变量的影响可能会被放大或减弱. 因此, 对于建立准确的交通运输碳排放预测模型来说, 一些重要程度排名较低的变量仍然需要被考虑进去.
3 政策建议(1)个体固定效应系数高的省份, 如上海、广东、辽宁和山东等, 应全方面采取减碳措施来降低交通碳排放量. 国家应该对高碳排放省份加强督促和监督, 确保它们能够按照减碳目标和要求实施减碳措施, 落实减碳政策. 此外, 政府可以建立碳排放权交易市场, 通过碳排放权交易的方式, 促进高碳排放省份的碳排放削减, 同时鼓励低碳省份在碳排放权交易市场上获得经济收益, 促进低碳发展. 另外, 政府可以推动建立全国性的碳排放数据平台, 通过数据监测和分析, 及时发现和解决高碳排放省份的问题, 促进碳排放削减.
(2)社会商品消费总额大与货运周转量大的省份往往具有人口密集、经济发达和城市化水平高等特点, 如广东、江苏和浙江等, 随着物流和货运的发展, 使得物流运输和货车运输等交通活动增加, 从而增加了交通碳排放量. 对于这样的省份, 通过发展多式联运, 例如铁路、水路和公路的协调运输, 可以降低物流运输的碳排放量. 尤其是采用铁路和水路等公共交通工具, 可以更大程度地减少碳排放量. 此外, 通过采用可再生能源, 例如太阳能和风能等, 为物流运输提供能源, 以减少物流运输的碳排放. 同时, 使用更高效的物流设备和技术, 如智能物流系统和电动物流设备等, 可以降低能源消耗和碳排放.
(3)随着城市化进程的推进, 城市人口密度增加, 导致交通量大, 城市拥堵现象比较普遍, 导致交通拥堵、行驶时间增加, 从而增加了交通排放量. 此外, 城市化还意味着城市的基础设施需求增加, 人口活动区域分散, 交通需求增加, 从而导致交通运输碳排放量增加. 政府可以鼓励居民选择步行、骑行和共享单车等低碳出行方式, 通过建设便捷的步行和骑行路线, 推广共享单车等方式, 提高居民选择低碳出行的便捷性和吸引力. 此外, 政府可以加强智能交通系统的建设, 通过交通信息化技术实现道路资源的优化配置, 减少交通拥堵和碳排放.
(4)政府可以鼓励居民使用公共交通工具, 例如地铁、公交车和轨道交通等, 通过提高公共交通服务质量、扩大公共交通覆盖范围等方式, 促进居民使用公共交通, 从而减少私家车出行, 降低交通碳排放量. 此外, 政府可以鼓励居民购买新能源汽车, 推广新能源汽车的使用, 逐步减少传统燃油车的使用, 降低交通碳排放量.
4 结论(1)根据变量相关性分析的结果, 可以看出, 在初步选取的18个解释变量中, 有11个解释变量通过了显著性检验. 以上变量包括省份差异、公共交通数量、社会商品消费总额、私家车数量、常住人口数量、货运周转量、城市绿地面积、交通运输业产值、城市桥梁数量、GDP和交通基础设施密度. 以上变量对中国交通运输CO2排放量的解释具有重要意义. 在以上变量中, 省份差异与交通碳排放量的相关性系数最高, 为0.86, 说明不同省份之间存在显著的交通碳排放量差异. 其次是公共交通数量, 相关性系数为0.84, 其他变量的相关性系数也比较高, 说明以上变量对交通碳排放量的影响也不容忽视.
(2)随机森林、XGBoost和KNN算法均能够对训练集和测试集进行较好地拟合, 训练集上R2均高于0.97, 测试集上R2均高于0.95, 且误差都低于10%, 其中, 随机森林算法、XGBoost算法在十折交叉验证中仍表现良好, R2均高于0.96, KNN算法的R2高于0.92, 认为表现欠佳. 总体而言, 随机森林与XGBoost算法均适合用于预测交通运输CO2排放量, 而KNN算法在本数据集上的表现有待提高, 不太适合构建交通运输碳排放预测模型. 综合MSE、MAE、R2和MAPE这4项指标来看, XGBoost算法取得了最佳结果. 因此本文认为, 在机器学习算法中, XGBoost算法最适合于用来构建交通运输碳排放预测模型.
(3)通过计算Model_xg中各输入变量的SHAP值得到变量重要性排名, 从高到低依次是:Pro、SSG、PC、UP、GN、GAS和TRP. 其中省份差异对于预测交通碳排放量而言是影响最大的因素, 因此, 在从国家层面进行交通碳排放预测时, 不可忽略省份因素.
| [1] |
庞可, 张芊, 马彩云, 等. 基于LEAP模型的兰州市道路交通温室气体与污染物协同减排情景模拟[J]. 环境科学, 2022, 43(7): 3386-3395. Pang K, Zhang Q, Ma C Y, et al. Forecasting of emission co-reduction of greenhouse gases and pollutants for the road transport sector in Lanzhou based on the LEAP model[J]. Environmental Science, 2022, 43(7): 3386-3395. |
| [2] |
王杰, 郑琰, 姜晓红. 西南地区交通运输业碳排放测算与驱动因素分析[J]. 重庆理工大学学报(自然科学), 2023, 37(1): 249-256. Wang J, Zheng Y, Jiang X H. Carbon emission measurement and driving factor analysis of the transportation industry in Southwest China[J]. Journal of Chongqing University of Technology (Natural Science), 2023, 37(1): 249-256. |
| [3] |
刘淳森, 曲建升, 葛钰洁, 等. 基于LSTM模型的中国交通运输业碳排放预测[J]. 中国环境科学, 2023, 43(5): 2574-2582. Liu C S, Qu J S, Ge Y J, et al. LSTM model-based prediction of carbon emissions from China's transportation sector[J]. China Environmental Science, 2023, 43(5): 2574-2582. DOI:10.3969/j.issn.1000-6923.2023.05.049 |
| [4] |
蒋自然, 金环环, 王成金, 等. 长江经济带交通碳排放测度及其效率格局(1985~2016年)[J]. 环境科学, 2020, 41(6): 2972-2980. Jiang Z R, Jin H H, Wang C J, et al. Measurement of traffic carbon emissions and pattern of efficiency in the Yangtze River economic belt (1985-2016)[J]. Environmental Science, 2020, 41(6): 2972-2980. |
| [5] |
刘慧甜, 胡大伟. 不同禁售时间下燃油车替代策略的减排效果分析[J]. 交通运输研究, 2022, 8(6): 40-52. Liu H T, Hu D W. Emission reduction effects of alternative strategies for fuel vehicle under different time banning the sale[J]. Transport Research, 2022, 8(6): 40-52. |
| [6] |
马菁, 蔡旭, 张春梅, 等. 考虑区域特点和车型差异的氢燃料电池汽车全生命周期减碳预测分析[J]. 环境科学, 2024, 45(2): 744-754. Ma J, Cai X, Zhang C M, et al. Carbon reduction analysis of life cycle prediction assessment of hydrogen fuel cell vehicles: considering regional features and vehicles type differences[J]. Environmental Science, 2024, 45(2): 744-754. |
| [7] |
王靖添, 马晓明. 中国交通运输碳排放影响因素研究——基于双层次计量模型分析[J]. 北京大学学报(自然科学版), 2021, 57(6): 1133-1142. Wang J T, Ma X M. Influencing factors of carbon emissions from transportation in China: empirical analysis based on two-level econometrics method[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2021, 57(6): 1133-1142. |
| [8] |
刘吉毅, 黄福友, 陈斌. 交通运输业碳排放影响因素及减排策略研究[J]. 公路, 2023, 68(5): 252-259. Liu J Y, Hung F Y, Chen B. Research on influencing factors and emission reduction strategies of carbon emission in transportation industry[J]. Highway, 2023, 68(5): 252-259. |
| [9] |
张兰怡, 卢秋萍, 张园园, 等. 福建省交通碳排放影响因素与减碳趋势研究[J]. 哈尔滨商业大学学报(自然科学版), 2022, 38(3): 360-366, 375. Zhang L Y, Lu Q P, Zhang Y Y, et al. Research on influencing factors and carbon reduction trend of transportation carbon emissions in Fujian Province[J]. Journal of Harbin University of Commerce (Natural Sciences Edition), 2022, 38(3): 360-366, 375. |
| [10] | Hassouna F M A, Al-Sahili K. Environmental impact assessment of the transportation sector and hybrid vehicle implications in Palestine[J]. Sustainability, 2020, 12(19). DOI:10.3390/su12197878 |
| [11] |
江心英, 朱蓉. 江苏省第二产业发展与碳排放关系研究——基于1987-2018年时间序列数据的实证分析[J]. 生态经济, 2022, 38(5): 28-32. Jiang X Y, Zhu R. Study on the relationship between the development of secondary industry and carbon emission in Jiangsu Province: an empirical analysis based on time series data from 1987 to 2018[J]. Ecological Economy, 2022, 38(5): 28-32. |
| [12] |
赵金辉, 李景顺, 王潘乐, 等. 基于Lasso-BP神经网络模型的河南省碳达峰路径研究[J]. 环境工程, 2022, 40(12): 151-156, 164. Zhao J H, Li J S, Wang P L, et al. A study on carbon peaking paths in Henan, China based on Lasso regression-BP neural network model[J]. Environmental Engineering, 2022, 40(12): 151-156, 164. |
| [13] |
卞利花, 吉敏全. 青海交通碳排放影响因素及预测研究[J]. 生态经济, 2019, 35(2): 35-39, 100. Bian L H, Ji M Q. Research on influencing factors and prediction of transportation carbon emissions in Qinghai[J]. Ecological Economy, 2019, 35(2): 35-39, 100. |
| [14] | Liu X H, Li W X, Li Y, et al. Quantifying environmental benefits of ridesplitting based on observed data from ridesourcing services[J]. Transportation Research Record: Journal of the Transportation Research Board, 2021, 2675(8): 355-368. |
| [15] |
李文翔, 李媛媛, 刘好德, 等. 基于机器学习的网约车合乘出行碳减排状态预测[J]. 交通运输系统工程与信息, 2023, 23(1): 254-264. Li W X, Li Y Y, Liu H D, et al. Prediction of CO2 emission reduction state of ridesplitting based on machine learning[J]. Journal of Transportation Systems Engineering and Information Technology, 2023, 23(1): 254-264. |
| [16] |
汤恒. 基于SPNN和GNNWR的碳排放预测模型研究——以长三角地区为例[D]. 南京: 南京邮电大学, 2022. Tang H. Research on carbon emission prediction based on SPNN and GNNWR models——take the Yangtze River Delta as an example[D]. Nanjing: Nanjing University of Posts and Telecommunications, 2022. |
| [17] | Nematchoua M K, Orosa J A, Afaifia M. Prediction of daily global solar radiation and air temperature using six machine learning algorithms; a case of 27 European countries[J]. Ecological Informatics, 2022, 69. DOI:10.1016/j.ecoinf.2022.101643 |
| [18] | Bakay M S, Ağbulut Ü. Electricity production based forecasting of greenhouse gas emissions in Turkey with deep learning, support vector machine and artificial neural network algorithms[J]. Journal of Cleaner Production, 2021, 285. DOI:10.1016/j.jclepro.2020.125324 |
| [19] |
张雯, 吴志彬, 徐玖平. 基于EMD-PSO-LSSVM的碳排分解集成预测方法[J]. 控制与决策, 2022, 37(7): 1837-1846. Zhang W, Wu Z B, Xu J P. A decomposition-integration forecasting method of carbon emission based on EMD-PSO-LSSVM[J]. Control and Decision, 2022, 37(7): 1837-1846. |
| [20] | Quej V H, Almorox J, Arnaldo J A, et al. ANFIS, SVM and ANN soft-computing techniques to estimate daily global solar radiation in a warm sub-humid environment[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2017, 155: 62-70. |
| [21] | 赵国锋, 高玉龙, 王仲. 基于决策树与蒙特卡洛仿真的交通碳排放分析方法[J]. 公路, 2015, 60(8): 191-195. |
| [22] |
夏晓圣, 陈菁菁, 王佳佳, 等. 基于随机森林模型的中国PM2.5浓度影响因素分析[J]. 环境科学, 2020, 41(5): 2057-2065. Xia X S, Chen J J, Wang J J, et al. PM2.5 concentration influencing factors in China based on the random forest model[J]. Environmental Science, 2020, 41(5): 2057-2065. |
| [23] | Sun W, Wang Y W, Zhang C C. Forecasting CO2 emissions in Hebei, China, through moth-flame optimization based on the random forest and extreme learning machine[J]. Environmental Science and Pollution Research, 2018, 25(29): 28985-28997. |
| [24] | Song Y F, Zhang Y Y, Liu J F, et al. Rural vehicle emission as an important driver for the variations of summertime tropospheric ozone in the Beijing-Tianjin-Hebei region during 2014-2019[J]. Journal of Environmental Sciences, 2022, 114: 126-135. |
| [25] | Wang Z H, Zhao Z J, Wang C X. Random forest analysis of factors affecting urban carbon emissions in cities within the Yangtze River economic belt[J]. PLoS One, 2021, 16(6). DOI:10.1371/journal.pone.0252337 |
| [26] | Tian X L, Huang G, Song Z Y, et al. Impact from the evolution of private vehicle fleet composition on traffic related emissions in the small-medium automotive city[J]. Science of the Total Environment, 2022, 840. DOI:10.1016/j.scitotenv.2022.156657 |
| [27] |
朱珈莹, 安俊琳, 冯悦政, 等. 基于轻量级梯度提升机的南京大气臭氧浓度预测[J]. 环境科学, 2023, 44(7): 3685-3694. Zhu J Y, An J L, Feng Y Z, et al. Atmospheric ozone concentration prediction in Nanjing based on LightGBM[J]. Environmental Science, 2023, 44(7): 3685-3694. |
| [28] |
吴迪, 杜宁, 王莉, 等. 基于GTWR-XGBoost模型的四川省PM2.5小时浓度估算[J]. 环境科学, 2023, 44(7): 3738-3748. Wu D, Du N, Wang L, et al. Estimation of PM2.5 hourly concentration in Sichuan Province based on GTWR-XGBoost model[J]. Environmental Science, 2023, 44(7): 3738-3748. |
| [29] |
张清华, 支学超, 王国胤, 等. 基于属性代表的多粒度集成分类算法[J]. 计算机学报, 2011, 34(8): 1399-1410. Zhang C X, Zhang J S. A survey of selective ensemble learning algorithms[J]. Chinese Journal of Computers, 2011, 34(8): 1399-1410. |
| [30] |
代园园, 龚绍琦, 张存杰, 等. 粤港澳大湾区大气PM2.5浓度的遥感估算模型[J]. 环境科学, 2024, 45(1): 8-22. Dai Y Y, Gong S Q, Zhang C J, et al. Remote sensing model for estimating atmospheric PM2.5 concentration in the Guangdong-Hong Kong-Macao greater bay area[J]. Environmental Science, 2024, 45(1): 8-22. |
| [31] | Magazzino C, Mele M, Schneider N. A machine learning approach on the relationship among solar and wind energy production, coal consumption, GDP, and CO2 emissions[J]. Renewable Energy, 2021, 167: 99-115. |
| [32] |
吴琼, 马昊, 任洪波, 等. 基于LEAP模型的临港新片区中长期碳排放预测及减排潜力分析[J]. 环境科学, 2024, 45(2): 721-731. Wu Q, Ma H, Ren H B, et al. Medium and long-term carbon emission projections and emission reduction potential analysis of Lingang special area based on the LEAP model[J]. Environmental Science, 2024, 45(2): 721-731. |
| [33] | Ağbulut Ü. Forecasting of transportation-related energy demand and CO2 emissions in Turkey with different machine learning algorithms[J]. Sustainable Production and Consumption, 2022, 29: 141-157. |
| [34] | Li X D, Ren A, Li Q. Exploring patterns of transportation-related CO2 emissions using machine learning methods[J]. Sustainability, 2022, 14(8). DOI:10.3390/su14084588 |
| [35] |
高金贺, 黄伟玲, 蒋浩鹏. 城市交通碳排放预测的多模型对比分析[J]. 重庆交通大学学报(自然科学版), 2020, 39(7): 33-39. Gao J H, Huang W L, Jiang H P. Comparison of multiple forecast models of urban traffic carbon emissions[J]. Journal of Chongqing Jiaotong University (Natural Science), 2020, 39(7): 33-39. |
| [36] |
胡茂峰, 郑义彬, 李宇涵. 多情景下湖北省交通运输碳排放峰值预测研究[J]. 环境科学学报, 2022, 42(4): 464-472. Hu M F, Zheng Y B, Li Y H. Forecasting of transport carbon emission peak in Hubei Province under multiple scenarios[J]. Acta Scientiae Circumstantiae, 2022, 42(4): 464-472. |
| [37] |
杨君. 中国交通运输业碳排放测度及减排路径研究[D]. 南昌: 江西财经大学, 2022. Yang J. A research on carbon emission measurement and reduction path of China's transportation[D]. Nanchang: Jiangxi University of Finance and Economics, 2022. |
| [38] |
郁小刚. 天津市交通运输业碳排放量影响因素及预测研究[D]. 天津: 天津理工大学, 2022. Yu X G. Research on the influencing factors and forecast of carbon emissions in Tianjin's transportation industry[D]. Tianjin: Tianjin University of Technology, 2022. |
| [39] |
曾晓莹, 邱荣祖, 林丹婷, 等. 中国交通碳排放及影响因素时空异质性[J]. 中国环境科学, 2020, 40(10): 4304-4313. Zeng X Y, Qiu R Z, Lin D T, et al. Spatio-temporal heterogeneity of transportation carbon emissions and its influencing factors in China[J]. China Environmental Science, 2020, 40(10): 4304-4313. |
| [40] | Guan Y R, Shan Y L, Huang Q, et al. Assessment to China's recent emission pattern shifts[J]. Earth's Future, 2021, 9(11). DOI:10.1029/2021EF002241 |
| [41] |
陈金车. 基于机器学习的西北省会城市空气污染物浓度预报方法研究[D]. 兰州: 兰州大学, 2022. Chen J C. Research on forecasting method of air pollutant concentration in northwest provincial capital cities based on machine learning[D]. Lanzhou: Lanzhou University, 2022. |
| [42] | Montes C, Kapelan Z, Saldarriaga J. Predicting non-deposition sediment transport in sewer pipes using random forest[J]. Water Research, 2021, 189. DOI:10.1016/j.watres.2020.116639 |
| [43] |
彭岩, 马铃, 张文静, 等. 基于集成学习的风险预测模型研究与应用[J]. 计算机工程与设计, 2022, 43(4): 956-961. Peng Y, Ma L, Zhang W J, et al. Research and application of risk forecast model based on ensemble learning[J]. Computer Engineering and Design, 2022, 43(4): 956-961. |
| [44] |
代鑫, 黄弘, 汲欣愉, 等. 基于机器学习的城市暴雨内涝时空快速预测模型[J]. 清华大学学报(自然科学版), 2023, 63(6): 865-873. Dai X, Huang H, Ji X Y, et al. Spatiotemporal rapid prediction model of urban rainstorm waterlogging based on machine learning[J]. Journal of Tsinghua University (Science and Technology), 2023, 63(6): 865-873. |
| [45] | Chou J S, Pham A D. Nature-inspired metaheuristic optimization in least squares support vector regression for obtaining bridge scour information[J]. Information Sciences, 2017, 399: 64-80. |
| [46] | 何萍, 杨宜平. 基于部分线性面板数据模型的碳排放分析和预测研究[J]. 统计理论与实践, 2023(1): 46-49. |
 2024, Vol. 45
2024, Vol. 45


