2. 中国地质大学(北京)数理学院, 北京 100083;
3. 北京农林科学院智能装备研究中心, 北京 100097;
4. 廊坊市灾害遥感监测重点实验室, 廊坊 065201;
5. 防灾科技学院生态环境学院, 廊坊 065201
2. School of Mathematics and Physics, China University of Geosciences (Beijing), Beijing 100083, China;
3. Research Center of Intelligent Equipment, Beijing Academy of Agriculture and Forestry Sciences, Beijing 100097, China;
4. Langfang Key Laboratory of Disaster Monitoring by Remote Sensing, Langfang 065201, China;
5. Institute of Disaster Prevention Science and Technology, Langfang 065201, China
土壤是粮食安全、水安全和更广泛的生态系统安全的基础. 随着社会经济高速发展, 长期以来高强度和超负荷的开发利用土地, 造成了耕地土壤环境质量的破坏, 其中土壤重金属污染日益严重, 成为备受关注的全球性问题. 土壤监测调查是准确掌握土壤重金属污染状况及变化趋势的主要技术手段[1]. 土壤监测调查受控于采样、化验等成本的限制, 相对于研究区总体来讲, 样本量往往相对稀疏, 不能精准刻画土壤污染空间分布特征, 在一定程度上使得土壤治理与风险防控受限[2]. 母质母岩、工矿企业排放(大气、水)及农业投入品和交通运输等影响因素与土壤重金属含量分布存在一定的空间同位性和属性相关性[3]. 基于上述自然和人为因素准确刻画土壤重金属的空间变化特征, 实现稀疏样点下土壤重金属含量高精度估计是当前土壤环境质量关注的热点, 在土壤重金属监测监管中具有重要的现实意义.
目前常用的土壤重金属含量估计方法有:基于空间位置相关性的方法, 如克里金插值方法和反距离加权法;基于属性相似的方法, 如朱阿兴等的地理学第三定理法[4]和机器学习法;以及基于综合空间相似性和属性相似性的方法[5], 如随机森林克里金法和回归克里金法等. 克里金插值方法通过已知样点对未知样点进行线性无偏和最优化估计, 样点需满足正态分布及或内蕴平稳假设, 同时会对数据结果进行平滑处理, 使局部异质点位或变化剧烈区的重要信息丢失, 尤其在极值和空间连续性模式敏感的应用中存在一定的局限性[6]. 为克服这一问题, Matheron[7]提出了转向带法, 其主要思路是先根据空间数据的统计特征模拟出一维随机变量, 然后将其在空间中旋转得到三维模拟, 该方法将数据作为一个整体, 引入未知点的最大可能值的概率, 最大可能地接近真实的空间分布结果, 具有与实测数据相同的频率直方图, 且模拟结果与实测结果具有相同的空间自相关关系. 随后又衍生出转向带法[8]、指示模拟法[9]、矩阵分解法[10]、蒙特卡罗法[11]、序贯指示模拟[12, 13]和序贯高斯模拟方法[14, 15]等. 赵永存等[16]以江苏省张家港市土壤镉含量为例对比不同条件模拟方法, 结果表明定量预测局部不确定性对于控制土壤空间数据的应用风险具有重要意义. Delbari等[17]验证了序贯高斯模拟能克服克里格的平滑效果, 更能真实地反映土壤有机碳的空间分布. 为了提高未知点统计推断结果精度, 基于空间相关性方法和条件模拟法往往需增加土壤采样密度, 提高样本量[18]. 人工神经网络[19]、回归树[20]、随机森林(RF)[21]和梯度提升决策树[22]等机器学习模型可以充分利用环境变量间属性特征, 通过建立未知点与土壤环境变量的非线性函数关系, 实现复杂空间分布下土壤属性预测[23]. 上述机器学习方法因其在处理多维连续型和类别型变量方面的优势, 逐渐发展成主流的土壤属性统计推断方法[24]. 其中, 随机森林模型是基于多个决策树的集成学习算法, 可以防止过拟合且预测效果稳定, 是一种有效的土壤预测方法. 然而土壤重金属具有多尺度特征[25, 26], 其空间分布特征也比较复杂, 既有小尺度的细节空间分布特征又具有大尺度的宏观分布特征, 将RF模型的预测残差与预测结果相结合的随机森林残差克里格法(RFRK)能提高随机森林模型的预测精度[27].
基于上述分析, 本文提出了基于随机森林-序贯高斯模拟混合模型, 在顾及土壤环境影响结构特征的基础上, 利用机器学习模型刻画土壤重金属全局的非线性和非平稳趋势面, 同时将具有空间自相关性的残差部分进行条件模拟, 通过结合空间信息和属性信息有效提升模型模拟精度, 解决土壤重金属空间分布特征复杂、局部变化异常点预测难的问题, 以期为区域土壤重金属含量准确估计提供一种可行的解决方案.
1 材料与方法 1.1 研究区概况顺义区位于北京市东北方向, 距市区30 km, 北邻怀柔区和密云区, 东界平谷区, 南与通州区和河北省三河市接壤, 西南和西与昌平区和朝阳区隔温榆河为界. 介于北纬40°00'~40°18', 东经116°28'~116°58'之间, 境域东西长45 km, 南北宽30 km, 总面积1 021 km2, 其中耕地面积404.05 km2, 占总面的39.56%. 地势北高南低, 区域内有大小河流20余条, 分属北运河、潮白河和蓟运河这3个水系, 河道总长232 km. 蓟运河水系主要支流金鸡河是顺义东南部的主要泄洪和排污河道, 小中河是顺义西南部的主要泄洪和排污河道. 土壤类型主要为潮土和褐土, 且潮土分布于全区大部分地区、褐土主要分布在东北部. 种植模式为冬小麦-夏玉米, 粮食生产用地占农业用地的56.91%, 其中南部是主要的菜地集中区域, 东北部则是果园的聚集地, 样点的分布见图 1.
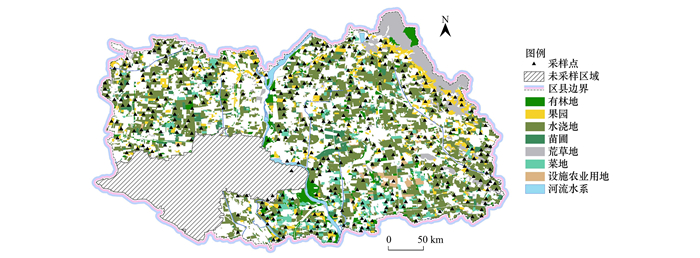
|
图 1 研究区点位分布示意 Fig. 1 Distribution of sites in the study area |
于2009年8~11月在顺义区农田采用混合采样方法, 共采集412个农田表层土壤样品(0~20 cm), 同时记录每个样点的经纬度坐标、土地利用方式、土壤类型、质地和施肥等相关信息. 每个采样点用木铲采集1.0 kg的土壤样品, 样品风干后过2.0 mm的初筛, 四分样后选取50 g的样品, 使用玛瑙研钵研磨后过0.15 mm的细筛. 土壤样品按照EPA Method 3050B的方法使用HNO3、HCL和H2O2混合溶液消解, 消解液中的砷、镉、铜、锌和铅使用等离子发射光谱仪(ICP-OES, Thermo iCAP 6300, USA)测定, 汞的测定使用1∶1的HNO3∶HCl在100℃消解, 消解液使用原子荧光光谱仪(AFS, Titan AFS830, China)测定. 每个样品设3个平行样, 样品处理和分析的质量控制采用分析土壤标准参考物质GSS-1和GSS-4(中国标准物质中心).
1.2 研究方法 1.2.1 随机森林-序贯高斯模拟方法随机森林-序贯高斯模拟混合方法(random forest with sequential Gaussian simulation, RF-SGS)是一种结合了随机森林(RF)与序贯高斯模拟(SGS)的混合地统计模型. 其中, 随机森林(RF)是一种基于多个决策树的数据挖掘算法, 通过在训练数据集中应用bootstrap方法随机抽取样本构建单独的树模型, 生成大量的树后组成随机森林, 与CART决策树模型相比, RF模型对过拟合不敏感[28]. 序贯高斯模拟主要是随机生成一条模拟路径, 逐步求取各个待估点处的累积条件分布函数, 并根据该累积条件分布函数求得该点的模拟值[29]. 本文通过随机森林在随机模型中引入协变量, 即在序贯高斯模拟中添加了确定性模型, 通过引入有效辅助变量来构建变量间的非线性关系. 通常情况残差被认为是误差, 代表模型中无法用确定性成分解释的成分[30]. 理想情况下, 模型的残差应该是相同且独立分布的. 有研究表明, 事实上残差在某些情况下表现为空间自相关[31].
Cd在空间上的分布宜受人类活动影响[32], 主要的自然和人为因素影响的趋势性部分可以通过随机森林模拟, 对于残差项部分的随机性可以看作随机过程, 多年累积中的随机过程可以用马尔可夫链模型表达[33]. 马尔可夫链模型是一种随机过程, 假设某一个系统发展过程有m个可能状态, 且各状态互不相容, 即 S(1), S(2), …, S(m), 初始概率向量S (0)表示为:
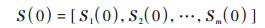
|
(1) |
经k步转移后, 状态i的概率向量:
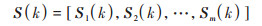
|
(2) |
S(0)与S(k)的关系可表示为:
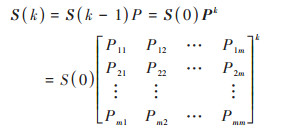
|
(3) |
当S(0)和转移概率P已知时, 可以用式(1)得到在k时刻系统所处的状态, 这就是马尔可夫模型. 用这个模型的关键是确定P, 再给定系统的初始状态向量S(0), 就可以得到某种情况下的状态向量S(k). 序贯高斯模拟条件累积过程可以用马尔可夫状态转移表达, 从而实现对随机性残差的空间分布模拟[34]. 因此本文在确定性分量上加入残差, 通过地统计条件模拟将空间自相关引入模型, 从而提高模拟精度. 具体步骤如下.
根据Pearson相关系数和方差分析探索连续型和分类型因素对土壤重金属含量影响是否显著, 由此选取辅助变量;利用随机森林拟合模型, 用实测值减去拟合值(即趋势项的影响)得残差值r;对残差值r进行序贯高斯模拟实现随机场生成, 得到模拟残差值;将趋势项部分和模拟残差部分结果进行相加, 得到最后预测值y. 通过以上步骤, 最终得到随机森林与序贯高斯模拟融合结果.
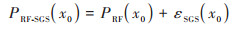
|
(4) |
式中, PRF-SGS(x0)为RF-SGS模型在x0位置的Cd含量预测值, PRF(x0)为趋势项, 通过RF模型拟合, 可影响因素εSGS(x0)为误差项, 通过对残差进行序贯高斯模拟拟合.
1.2.2 实验设计与精度评价本文选取区域土壤重金属Cd作为研究对象, 将412个高密度样点看作研究“总体”进行抽稀, 基于不同样本密度对本文提出的随机森林-序贯高斯模拟模型(RF-SGS)、序贯高斯模拟模型(SGS)、随机森林模型(RF)和趋势面-序贯高斯模拟模型(TR-SGS)分别建立模型, 并对比4种模型预测结果的数值分布和空间分布, 进行估计精度的分析和评价.
为了更好地评估模型精度, 本文以7∶3的比例划分训练集和验证集, 选取平均绝对误差(MAE)、平均相对误差(MRE)和均方根误差(RMSE)作为评价指标, 对比SGS模型、TR-SGS模型、RF模型和RF-SGS模型的估计结果与实际对应的采样点观测数据接近程度, 进而评估模型预测结果的准确性, 以验证RF-SGS模型是否能有效提高模拟精度.
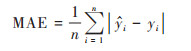
|
(5) |
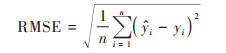
|
(6) |
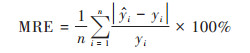
|
(7) |
式中, 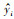
为进一步验证模拟数据和实际值之间偏差, 使用预测结果与样本点的相对误差的绝对值来测度拟合偏差RE[35], 设定均值相对误差(relative error of mean, REM)、离散系数相对误差(relative error of dispersion coefficient, RED)、偏度系数相对误差(relative error of skewness, RES)和峰度系数相对误差(relative error of kurtosis, REK)指标, 表征拟合结果与实际值之间差异.
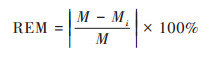
|
(8) |
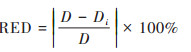
|
(9) |
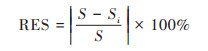
|
(10) |
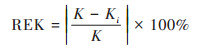
|
(11) |
式中, M、D、S和K分别为采样点实际均值、离散系数、偏度系数和峰度系数, Mi、Di、Si和Ki分别为4种模拟方法下验证集的均值、离散系数、偏度系数和峰度系数.
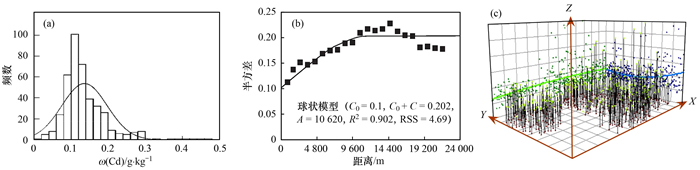
2 结果与分析 2.1 土壤重金属空间特征分析对顺义区412个采样点Cd含量数据进行描述性统计分析, 以反映研究区土壤重金属的总体空间分布特征(见表 1), 其中ω(Cd)范围为0.015 ~ 0.469 g·kg-1, 均值为0.136 g·kg-1, 高于背景值0.12 g·kg-1[36];标准差为0.06 g·kg-1, 偏度系数为2, 峰度系数为6.36, 变异系数为0.45, 属于中等变异. 结合样点的含量直方图[图 2(a)], 可知顺义区土壤Cd含量受到人类活动影响, 呈右偏态分布.
|
|
表 1 不同采样方案描述性统计1) Table 1 Descriptive statistics for different sampling schemes |
|
(a)Cd含量直方图, (b)Cd半方差函数及参数, (c)Cd趋势效应;(b)中C0为块金值, C0+C为基台值, A为变程;(c)中蓝线为重金属Cd含量在南北方向的变化趋势, 绿线为东西方向的变化趋势, 线段高度表示此点处Cd含量值 图 2 Cd数据特征 Fig. 2 Cd data feature |
对研究区土壤Cd进行空间变异函数拟合[图 2(b)], 其块金系数为0.5, 表明在空间上具有中等程度的变异性, 即存在由人为因素和自然因素共同作用产生的空间变异. 从土壤Cd含量区域趋势[图 2(c)]也可以看出, 东西方向呈线性或一阶趋势, Cd含量的分布具有一定趋势性;南北方向呈二阶多项式变化, 也说明Cd含量的分布还存在均值或者方差非平稳特征;上述特点可能受土壤类型、质地、土地利用和工矿企业排放局部污染等的影响, 适合采用上述方法进行区域土壤含量的建模研究.
2.2 环境变量选取及实验方案生成为了表征土壤重金属受自然因素和人为活动的影响, 即反映模型中PRF(x0)项, 本文选取表 2中的土壤、气候、人类活动以及地理位置等10个代理变量, 对研究区土壤重金属Cd进行模拟. 通过搜集对比近5年人为影响因素变化情况, 发现土地利用类型、PM10和距污染企业距离因素变化较小, 因此本文采集2009年数据作为代理变量进行建模研究. 其中土壤类型和土壤质地、酸碱度用于反映土壤的差异性和趋势性;年均降水量和归一化植被指数反映成土条件及成土过程等因素差异性和趋势性;经度和纬度代表调查点地理位置空间自相关性;距离污染企业距离、可吸入颗粒物PM10、土地利用方式代表企业、农业投入品强度等点源和面源等人类活动影响因素的空间异质性;使用ArcMap 10.5中多值提取到点工具将各辅助变量值提取到对应采样点, 生成实验数据集.
|
|
表 2 数据类型与来源1) Table 2 Data type and source |
使用皮尔逊相关系数计算连续型变量与Cd含量之间的关系, 使用方差分析[37]判别类别型变量对土壤重金属含量是否有显著影响, 选择与Cd存在较高相关性的要素作为预测模型的输入. 表 3为连续型变量与Cd含量之间的相关性. 从中可知, Cd含量与DTPE、MAP、pH、LON和PM10呈正相关关系, 与LAT和NDVI呈现负相关关系. 同时, Cd含量与LAT、DTPE和pH均呈现较强的相关性关系. 基于上述分析选择合适的辅助变量进行Cd空间分布预测.
|
|
表 3 连续型变量与Cd含量的相关性1) Table 3 Analysis of correlation for continuous variables and Cd concerntration |
表 4为类别型变量与Cd含量的方差分析检验结果. 从中可知, LUT、STP和ST这3个分类变量与Cd含量的方差分析检验结果均在0.05的水平下显著(P < 0.05), 说明土地利用方式、土壤类型和土壤质地在该研究区内对土壤重金属Cd的含量具有一定的影响.
|
|
表 4 类别型变量方差分析检验结果 Table 4 Spatial heterogeneity test results for categorical variables |
为了验证模拟的稳健性, 以研究区412个高密度土壤采样为基础, 通过平均最短距离最小化准则(minimization of the mean of the shortest distance, MMSD)对样本进行抽稀[38], 模拟实际采样的真实情况. 该算法的核心思想是使采样点在整个空间分布尽可能均匀, 从而使抽样空间内任意一个空间位置点与它最邻近点之间的距离的期望最小[39], 该方法在土壤调查和土壤制图中得到广泛应用, 其公式见式(12).
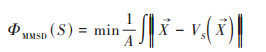
|
(12) |
式中, S为抽样样本;A为抽样总体;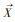
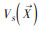
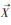
MMSD采样个数分别为50、100、150、200、250、300和350的样本点, 模拟不同密度的采样情况. 为降低采样随机性的影响, 本文对不同采样密度的样本分别进行200次重复, 并取200次计算结果的平均值作为最终结果, 抽稀过程使用R语言实现, 如图 3所示.
|
图 3 不同采样密度方案设计 Fig. 3 Different sampling density scheme design |
样本抽稀后各统计值见表 1, 不同抽样密度下统计量值有微小浮动, 随着样本个数增加, 各密度下样本统计指标也更接近原始数据, 可见抽稀后样本存在良好的稳定性.
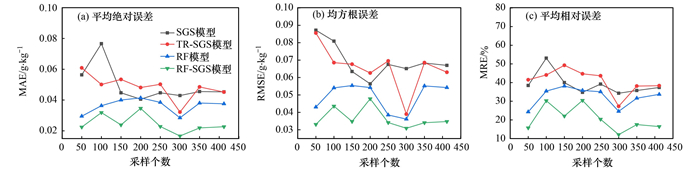
2.3 模拟结果对比分析对比4种模型对重金属Cd含量的预测精度, 结果如图 4所示. 在不同抽稀密度下, SGS模型、TR-SGS模型、RF模型和RF-SGS模型的MAE均值分别为0.045、0.045、0.038和0.023 g·kg-1, RMSE均值分别为0.067、0.063、0.054和0.035 g·kg-1, MRE均值分别为37.38%、38.34%、33.67和16.42%. 可见, 在未采用辅助数据时, TR-SGS模型整体要优于SGS模型, 但该方法在不同采样密度下不够稳健, 在样点密度小时其误差大于SGS模型, 模型优化效果不够显著. 在采用辅助数据时, RF模型基于引入辅助变量构建非线性拟合, 其拟合效果优于SGS模型与TR-SGS模型. RF-SGS模型在MAE、RMSE、MRE这3个模型精度评价指标上的表现均显著优于SGS模型、TR-SGS模型和RF模型, 进而验证了RF-SGS模型的准确性和稳健性, 这种能力归因于它在RF模型中处理重金属Cd含量和环境辅助变量之间非线性关系的能力, 以及SGS模型残差中处理未解释信息的能力[40]. 综上, 由于样本抽稀过程RF-SGS模型模拟效果均优于传统模型, 证实RF-SGS模型可应用于不同采样密度下的土壤重金属空间分布模拟.
|
图 4 不同模型Cd模拟精度对比 Fig. 4 Comparison of Cd simulation accuracy of different models |
分别使用4种预测模型绘制研究区土壤重金属Cd空间分布, 如图 5所示, 可见研究区4种预测模型的土壤重金属Cd预测空间分布趋势整体表现一致, Cd的空间分布存在异质性, 与空间变异性分析吻合. Cd含量均表现为高值集中在南部和东北部, 中部地区的Cd整体含量偏低, 局部含量分布不均、呈现高低错落, 与趋势分析走势大致相符. 预测精度相对较低的SGS模型绘制的空间分布图存在边界较明显的块状区域, 且相比其他3种方法SGS模型在中部存在区域高值. 预测精度最优的RF-SGS模型预测结果中无边界明显的块状区域, 高值区中存在零星低值, 在低值区域存在零星高值, 并且值域范围最大, 与统计结果和研究区Cd空间分布更接近.
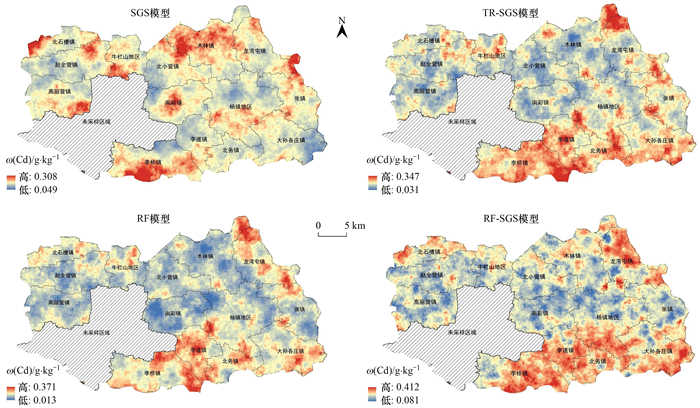
|
图 5 4种模型模拟结果空间分布 Fig. 5 Spatial distribution of simulation results of four models |
从土壤重金属空间特征分析可知, 顺义区Cd既存在空间相关性, 又存在局部空间异质性, 影响因素对土壤重金属分布有一定影响. 当未引入辅助变量时, 仅基于空间相关性的SGS模型, 其RMSE为0.067 g·kg-1, MAE为0.045 g·kg-1, MRE为37.38%, 能够达到较为可靠的空间拟合精度. SGS模型适用于平稳区域或者较密集采样点的情况, 或者在协变量难以收集或相关性不高时, 可以降低精度要求, 采用仅依赖空间相关性的模拟方法.
TR-SGS模型仅采用多项式构建确定性趋势面、再引入残差空间影响的方法, 适用于研究区具有明显一阶或多阶趋势分布的情况, 但在趋势的选择上通过直观判别可能会存在偏差, 选择符合度高的多项式拟合趋势面可以提高模拟精度, 本研究区TR-SGS模型的RMSE为0.063 g·kg-1, MAE为0.045 g·kg-1, MRE为38.34%, 对比SGS模拟精度提升不明显, 且在样本抽稀过程该方法稳健性较差, 50点和200点时拟合误差高于SGS模型.
引入辅助变量的RF模型拟合精度优于SGS模型和TR-SGS模型(图 4). 其原因在于土壤重金属与地理位置、距离因子、气候因子、植被因子等环境因素以及用地类型等人类活动密切相关, 具有较强的空间异质性[41, 42]. 通过引入与Cd相关的NDVI、PM10和年均降水量等多种环境变量, 利用属性相似性建模, 能够取得高于仅考虑空间相关性方法的精度. 因此, 能够处理多维多类型协变量的机器学习方法在土壤重金属反演中应用较多[43]. RF-SGS模型同时考虑了空间相关性和属性相似性, 对两者分别进行建模. 在50~412个采样点数量下其MAE和RMSE误差曲线均较其他3种方法效果更优, 且通过模拟结果对比(图 6)得到RF-SGS模型的模拟结果更接近真实情况. 因此, RF-SGS模型的模拟精度比SGS模型、TR-SGS模型和RF模型有所改进, 适用于非平稳和稀疏样点下的空间分布预测. 兼顾空间异质性和相关性进行建模的思想在相关领域也得到了学者的认可, 刘艳芳等[44]发现使用考虑残差空间结构的回归克里格模型预测土壤有机碳密度的表现优于其它模型.

|
x和y轴表示经纬度(°), z轴表示重金属Cd含量(g·kg-1) 图 6 Cd原始数据和模拟结果的对比 Fig. 6 Comparison of Cd's original data and simulated results |
以样本量为412时的全部模拟结果为例, 从模拟后空间分布基本趋势与原始数据的接近程度来检验模拟效果[45, 46], 从Cd实测数据、SGS模型、RF模型以及RF-SGS模型模拟结果的三维立体图可以看出(图 6), RF-SGS模型模拟结果的空间分布趋势与实测数据是最接近的. 未采用辅助数据的SGS模型预测结果在区域内整体偏高;TR-SGS模型由于趋势面拟合时没有引入辅助数据且仅采用多项式函数拟合, 模拟结果在高值和低值区刻画都不够准确, 出现低值偏低和高值偏高的情况. 加入辅助数据后的RF模型整体拟合趋势更接近实际情况, 但在东部高值区存在拟合偏高的误差, 其原因可能是模型拟合时仅考虑属性相关, 没有融合空间相关性建模. RF-SGS模型可通过残差空间性对RF模型拟合中偏离实际值的空间点位含量实现修正, 从而达到全局拟合效果最接近于实际的模拟结果.
从采样数量为412时4种模型全部模拟结果与原始数据的统计量相对误差对比可知(表 5), TR-SGS模型相对SGS模型REM、RED、RES和REK这4个误差统计量下降不够明显, 引入辅助变量的RF模型相对SGS模型, TR-SGS模型误差有显著下降, RF-SGS模型4个统计量的相对误差均为最小, 结合图 6空间分布可得, RF-SGS模型拟合效果最好, 整体数据分布与原始数据最接近.
|
|
表 5 统计量相对误差对比 Table 5 Statistical relative error comparison |
综上, RF-SGS模型能够有效提升未知空间模拟精度, 其模拟结果与原始数据中Cd含量更接近、空间分布格局特征更吻合, 证明了该方法的有效性与可行性, 可用于空间非平稳态下土壤重金属的空间模拟. 相较其他3种方法RF-SGS模型的优势有以下3点:首先, RF-SGS模型中RF部分具有非线性映射能力, 其考虑了包含自然和人为方面的多源辅助变量的确定性影响, 能以较高精度逼近任意连续函数;其次, RF-SGS模型的SGS部分将具有空间相关性的随机残差表示为随机变量, 对RF模型预测的不确定性部分进行条件模拟, 能够在尊重原始数据的基础上较好地反映土壤Cd含量空间变化;最后, RF-SGS模型可以改善单一机器学习与地统计模型面临的不稳定性, 单一机器学习容易受研究对象空间相关程度影响, 机器学习忽略空间性只考虑属性相关, RF-SGS模型将属性相关和空间相关相结合, 可更精确地描述土壤Cd含量的空间变化特征.
本文在对土壤重金属Cd进行建模时, 通过模型精度对比分析发现, 重金属的样点密度、样点空间结构以及辅助变量数据质量对于模拟效果有一定影响. 第一, 在非平稳区域中RF-SGS模型在不同密度下均保持有效性及稳健性. 第二, 部分人为活动因素的辅助变量数据未纳入建模过程, 如果将更多的人为活动因素, 比如耕作制度、施肥类型、施用量等作为协变量纳入模型, 可能会在一定程度上提高模型模拟精度.
4 结论(1)对于存在空间异质性的研究区, 基于自然和人类活动等影响因素建模, 利用RF模型和RF-SGS模型对区域土壤重金属含量模拟, 比未采用辅助数据的SGS模型和TR-SGS模型其未知点估算的精度有所提升, 在稀疏样本下运用有效辅助变量模拟效果更优.
(2)将机器学习与地统计建模融合的RF-SGS模型, 可以兼顾环境变量的属性相似性和人为活动局部影响的空间相关性, 在不同采样密度下, 其RMSE、MAE和MRE较其它3种模型均为最低, 且模拟结果与实际数据具有更相似的空间分布, 该方法可以用于空间非平稳、样本稀疏下未知点的土壤环境质量的估算.
| [1] | Sun X F, Zhang L X, Lv J S. Spatial assessment models to evaluate human health risk associated to soil potentially toxic elements[J]. Environmental Pollution, 2021, 268. DOI:10.1016/j.envpol.2020.115699 |
| [2] | Qu M K, Guang X, Liu H B, et al. Additional sampling using in-situ portable X-ray fluorescence (PXRF) for rapid and high-precision investigation of soil heavy metals at a regional scale[J]. Environmental Pollution, 2022, 292. DOI:10.1016/j.envpol.2021.118324 |
| [3] |
傅婷婷. 区域土壤和水稻镉含量相关分析与估测研究[D]. 杭州: 浙江大学, 2021. Fu T T. Regional research of correlation analysis and estimation of Cd content in soil and rice[D]. Hangzhou: Zhejiang University, 2021. |
| [4] |
朱阿兴, 闾国年, 周成虎, 等. 地理相似性: 地理学的第三定律[J]. 地球信息科学学报, 2020, 22(4): 673-679. Zhu A X, Lv G N, Zhou C H, et al. Geographic Similarity: Third Law of Geography?[J]. Journal of Geo-information Science, 2020, 22(4): 673-679. |
| [5] |
王雨雪, 杨柯, 高秉博, 等. 基于两点机器学习方法的土壤有机质空间分布预测[J]. 农业工程学报, 2022, 38(12): 65-73. Wang Y X, Yang K, Gao B B, et al. Prediction of the spatial distribution of soil organic matter based on two-point machine learning method[J]. Transactions of the Chinese Society of Agricultural Engineering, 2022, 38(12): 65-73. |
| [6] |
谢云峰, 陈同斌, 雷梅, 等. 空间插值模型对土壤Cd污染评价结果的影响[J]. 环境科学学报, 2010, 30(4): 847-854. Xie Y F, Chen T B, Lei M, et al. Impact of spatial interpolation methods on the estimation of regional soil Cd[J]. Acta Scientiae Circumstantiae, 2010, 30(4): 847-854. |
| [7] | Matheron G. The intrinsic random functions and their applications[J]. Advances in Applied Probability, 1973, 5(3): 439-468. DOI:10.2307/1425829 |
| [8] |
李少龙, 张家发, 张伟, 等. 表层土渗透系数空间变异与随机模拟研究[J]. 岩土力学, 2009, 30(10): 3168-3172. Li S L, Zhang J F, Zhang W, et al. Study of spatial variability and stochastic modeling of surface soil permeability[J]. Rock and Soil Mechanics, 2009, 30(10): 3168-3172. |
| [9] |
杨颢, 宋英强, 胡月明, 等. 基于序贯指示模拟的农田土壤重金属风险区域识别[J]. 应用生态学报, 2018, 29(5): 1695-1704. Yang H, Song Y Q, Hu Y M, et al. Using sequential indicator simulation method to define risk areas of soil heavy metals in farmland[J]. Chinese Journal of Applied Ecology, 2018, 29(5): 1695-1704. |
| [10] | Qiao P W, Dong N, Yang S C, et al. Quantitative analysis of the main sources of pollutants in the soils around key areas based on the positive matrix factorization method[J]. Environmental Pollution, 2021, 273. DOI:10.1016/j.envpol.2021.116518 |
| [11] |
佟瑞鹏, 杨校毅. 基于蒙特卡罗模拟的土壤环境健康风险评价: 以PAHs为例[J]. 环境科学, 2017, 38(6): 2522-2529. Tong R P, Yang X Y. Environmental health risk assessment of contaminated soil based on Monte Carlo method: a case of PAHs[J]. Environmental Science, 2017, 38(6): 2522-2529. |
| [12] |
徐辰星. 宜兴市土壤重金属分布特征与不确定性分析[D]. 南京: 南京大学, 2018. Xu C X. Distribution and uncertainties evaluation of soil heavy metals in Yixing, Yangtze River delta, China[D]. Nanjing: Nanjing University, 2018. |
| [13] |
孙雪菲, 张丽霞, 董玉龙, 等. 典型石化工业城市土壤重金属源解析及空间分布模拟[J]. 环境科学, 2021, 42(3): 1093-1104. Sun X F, Zhang L X, Dong Y L, et al. Source apportionment and spatial distribution simulation of heavy metals in a typical petrochemical industrial city[J]. Environmental Science, 2021, 42(3): 1093-1104. |
| [14] |
宋志廷, 赵玉杰, 周其文, 等. 基于地质统计及随机模拟技术的天津武清区土壤重金属源解析[J]. 环境科学, 2016, 37(7): 2756-2762. Song Z T, Zhao Y J, Zhou Q W, et al. Applications of geostatistical analyses and stochastic models to identify sources of soil heavy metals in Wuqing district[J]. Environmental Science, 2016, 37(7): 2756-2762. |
| [15] |
张泽浦, 王学军. 土壤微量元素含量空间分布的条件模拟[J]. 土壤学报, 1998, 35(3): 423-429. Zhang Z P, Wang X J. Conditional simulation for spatial distribution of trace elements in soils[J]. Acta Pedologica Sinica, 1998, 35(3): 423-429. |
| [16] |
赵永存, 孙维侠, 黄标, 等. 不同随机模拟方法定量土壤镉含量预测的不确定性研究[J]. 农业环境科学学报, 2008, 27(1): 139-146. Zhao Y C, Sun W X, Huang B, et al. Comparison of sequential indicator simulation and sequential indicator co-simulation for quantifying the local uncertainty of soil Cd content[J]. Journal of Agro-Environment Science, 2008, 27(1): 139-146. |
| [17] | Delbari M, Loiskandl W, Afrasiab P. Uncertainty assessment of soil organic carbon content spatial distribution using geostatistical stochastic simulation[J]. Australian Journal of Soil Research, 2010, 48(1): 27-35. DOI:10.1071/SR09026 |
| [18] | Han J Q, Mao K B, Xu T R, et al. A soil moisture estimation framework based on the CART algorithm and its application in China[J]. Journal of Hydrology, 2018, 563: 65-75. DOI:10.1016/j.jhydrol.2018.05.051 |
| [19] | Dharumarajan S, Lalitha M, Niranjana K V, et al. Evaluation of digital soil mapping approach for predicting soil fertility parameters—a case study from Karnataka Plateau, India[J]. Arabian Journal of Geosciences, 2022, 15(5). DOI:10.1007/s12517-022-09629-8 |
| [20] | Gardin L, Chiesi M, Fibbi L, et al. Mapping soil organic carbon in Tuscany through the statistical combination of ground observations with ancillary and remote sensing data[J]. Geoderma, 2021, 404. DOI:10.1016/j.geoderma.2021.115386 |
| [21] | Were K, Bui D T, Dick Ø B, et al. A comparative assessment of support vector regression, artificial neural networks, and random forests for predicting and mapping soil organic carbon stocks across an Afromontane landscape[J]. Ecological Indicators, 2015, 52: 394-403. DOI:10.1016/j.ecolind.2014.12.028 |
| [22] | Chen S C, Liang Z Z, Webster R, et al. A high-resolution map of soil pH in China made by hybrid modelling of sparse soil data and environmental covariates and its implications for pollution[J]. Science of the Total Environment, 2019, 655: 273-283. DOI:10.1016/j.scitotenv.2018.11.230 |
| [23] | Breiman L. Statistical modeling: The two cultures (with comments and a rejoinder by the author)[J]. Statistical Science, 2001, 16(3): 199-231. DOI:10.1214/ss/1009213725 |
| [24] | Zeraatpisheh M, Ayoubi S, Jafari A, et al. Digital mapping of soil properties using multiple machine learning in a semi-arid region, central Iran[J]. Geoderma, 2019, 338: 445-452. DOI:10.1016/j.geoderma.2018.09.006 |
| [25] | Sekulić A, Kilibarda M, Heuvelink G B M, et al. Random forest spatial interpolation[J]. Remote Sensing, 2020, 12(10). DOI:10.3390/rs12101687 |
| [26] |
刘伟, 郜允兵, 周艳兵, 等. 农田土壤重金属空间变异多尺度分析——以北京顺义土壤Cd为例[J]. 农业环境科学学报, 2019, 38(1): 87-94. Liu W, Gao Y B, Zhou Y B, et al. Multi scale analysis of spatial variability of heavy metals in farmland soils: Case study of soil Cd in Shunyi District of Beijing, China[J]. Journal of Agro-Environment Science, 2019, 38(1): 87-94. |
| [27] | Wang L, Wu W, Liu H B. Digital mapping of topsoil pH by random forest with residual kriging (RFRK) in a hilly region[J]. Soil Research, 2019, 57(4): 387-396. DOI:10.1071/SR18319 |
| [28] |
刘焕军, 张美薇, 杨昊轩, 等. 多光谱遥感结合随机森林算法反演耕作土壤有机质含量[J]. 农业工程学报, 2020, 36(10): 134-140. Liu H J, Zhang M W, Yang H X, et al. Invertion of cultivated soil organic matter content combining multi-spectral remote sensing and random forest algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering, 2020, 36(10): 134-140. |
| [29] |
刘兴业, 李景叶, 陈小宏, 等. 联合多点地质统计学与序贯高斯模拟的随机反演方法[J]. 地球物理学报, 2018, 61(7): 2998-3007. Liu X Y, Li J Y, Chen X H, et al. A stochastic inversion method integrating multi-point geostatistics and sequential Gaussian simulation[J]. Chinese Journal of Geophysics, 2018, 61(7): 2998-3007. |
| [30] |
许尔琪, 张红旗. 伊犁新垦区土壤有机质的克里金插值和条件模拟多尺度分析[J]. 土壤, 2013, 45(1): 91-98. Xu E Q, Zhang H Q. Multi-scale Analysis of kriging interpolation and conditional simulation for soil organic matters in newly reclaimed area in Yili[J]. Soils, 2013, 45(1): 91-98. |
| [31] | Tan Z, Yang Q, Zheng Y. Machine learning models of groundwater arsenic spatial distribution in Bangladesh: Influence of Holocene sediment depositional history[J]. Environmental Science & Technology, 2020, 54(15): 9454-9463. |
| [32] |
刘志鹏, 邵明安, 王云强. 区域尺度下黄土高原土壤全钾含量的空间模拟[J]. 农业工程学报, 2012, 28(22): 132-140. Liu Z P, Shao M A, Wang Y Q. Spatial simulation of soil total potassium in regional scale for Loess Plateau Region[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012, 28(22): 132-140. |
| [33] |
王绍武, 沈润平, 陈萍萍, 等. 基于马尔可夫链模型的华中地区土壤质地空间分布模拟研究[J]. 河南农业大学学报, 2019, 53(2): 282-288. Wang S W, Shen R P, Chen P P, et al. Simulation study on spatial distribution of soil texture based on Markov-chain model in central China[J]. Journal of Henan Agricultural University, 2019, 53(2): 282-288. |
| [34] |
李丹凤, 邵明安. 一维马尔可夫链模拟黑河中游流域土壤质地垂向变异[J]. 农业工程学报, 2013, 29(5): 71-80. Li D F, Shao M A. One-dimensional Markov chain simulation of vertical change of soil texture in middle reaches of Heihe river northwest China[J]. Transactions of the Chinese Society of Agricultural Engineering, 2013, 29(5): 71-80. |
| [35] |
任旭红, 潘瑜春, 高秉博, 等. 类别辅助变量参与下的土壤无偏采样布局优化方法[J]. 农业工程学报, 2014, 30(21): 120-128. Ren X H, Pan Y C, Gao B B, et al. Optimization method of unbiased soil sampling and layout using categorical auxiliary variables information[J]. Transactions of the Chinese Society of Agricultural Engineering, 2014, 30(21): 120-128. |
| [36] |
陈同斌, 郑袁明, 陈煌, 等. 北京市土壤重金属含量背景值的系统研究[J]. 环境科学, 2004, 25(1): 117-122. Chen T B, Zheng Y M, Chen H, et al. Background concentrations of soil heavy metals in Beijing[J]. Environmental Science, 2004, 25(1): 117-122. |
| [37] | Li B H, Tan C H. Distribution and risk evaluation of heavy metal in the soil of typical grassed swale[J]. MATEC Web of Conferences, 2016, 59. DOI:10.1051/matecconf/20165904001 |
| [38] |
刘明杰, 徐卓揆, 郜允兵, 等. 基于机器学习的稀疏样本下的土壤有机质估算方法[J]. 地球信息科学学报, 2020, 22(9): 1799-1813. Liu M J, Xu Z K, Gao Y B, et al. Estimating soil organic matter based on machine learning under sparse sample[J]. Journal of Geo-information Science, 2020, 22(9): 1799-1813. |
| [39] |
姜成晟, 王劲峰, 曹志冬. 地理空间抽样理论研究综述[J]. 地理学报, 2009, 64(3): 368-380. Jiang C S, Wang J F, Cao Z D. A review of geo-spatial sampling theory[J]. Acta Geographica Sinica, 2009, 64(3): 368-380. |
| [40] |
周洋, 赵小敏, 郭熙. 基于多源辅助变量和随机森林模型的表层土壤全氮分布预测[J]. 土壤学报, 2022, 59(2): 451-460. Zhou Y, Zhao X M, Guo X. Prediction of total nitrogen distribution in surface soil based on multi-source auxiliary variables and random forest approach[J]. Acta Pedologica Sinica, 2022, 59(2): 451-460. |
| [41] | Zhang W C, Wan H S, Zhou M H, et al. Soil total and organic carbon mapping and uncertainty analysis using machine learning techniques[J]. Ecological Indicators, 2022, 143. DOI:10.1016/j.ecolind.2022.109420 |
| [42] |
高中原, 肖荣波, 王鹏, 等. 融合自然-人为因子改进回归克里格对土壤镉空间分布预测[J]. 环境科学, 2021, 42(1): 343-352. Gao Z Y, Xiao R B, Wang P, et al. Improved regression Kriging prediction of the spatial distribution of the soil cadmium by integrating natural and human factors[J]. Environmental Science, 2021, 42(1): 343-352. |
| [43] |
谢恩泽, 赵永存, 陆访仪, 等. 不同方法预测苏南农田土壤有机质空间分布对比研究[J]. 土壤学报, 2018, 55(5): 1051-1061. Xie E Z, Zhao Y C, Lu F Y, et al. Comparison Analysis of methods for prediction of spatial distribution of soil organic matter contents in farmlands south Jiangsu, China[J]. Acta Pedologica Sinica, 2018, 55(5): 1051-1061. |
| [44] |
刘艳芳, 宋玉玲, 郭龙, 等. 结合高光谱信息的土壤有机碳密度地统计模型[J]. 农业工程学报, 2017, 33(2): 183-191. Liu Y F, Song Y L, Guo L, et al. Geostatistical models of soil organic carbon density prediction based on soil hyperspectral reflectance[J]. Transactions of the Chinese Society of Agricultural Engineering, 2017, 33(2): 183-191. |
| [45] | Facchinelli A, Sacchi E, Mallen L. Multivariate statistical and GIS-based approach to identify heavy metal sources in soils[J]. Environmental Pollution, 2001, 114(3): 313-324. DOI:10.1016/S0269-7491(00)00243-8 |
| [46] | Chi Y, Sun J K, Li T, et al. Spatial simulations of soil content, storage, and quality indices in an archipelago off the Yangtze River Estuary, China[J]. Ecological Indicators, 2023, 146. DOI:10.1016/j.ecolind.2022.109774 |
 2024, Vol. 45
2024, Vol. 45


