基于地统计模型的上海大气污染物多建模方法的比较

引用本文

吴英晗, 许嘉, 段玉森, 伏晴艳, 杨文. 基于地统计模型的上海大气污染物多建模方法的比较[J]. 环境科学, 2023, 44(10): 5370-5381.

WU Ying-han, XU Jia, DUAN Yu-sen, FU Qing-yan, YANG Wen. A Comparison Study on Multiple Modeling Approaches for Air Pollutant Geographic Model Development in Shanghai[J]. Environmental Science, 2023, 44(10): 5370-5381.

基于地统计模型的上海大气污染物多建模方法的比较

吴英晗¹, 许嘉¹, 段玉森², 伏晴艳², 杨文¹

1. 中国环境科学研究院, 北京 100012;
2. 上海市环境监测中心, 上海 200235

收稿日期: 2022-11-03; 修订日期: 2022-11-29

基金项目: 上海市科技支撑计划项目（20dz1204000）；中央财政科技计划结余经费（2021-JY-35）

作者简介: 吴英晗(2000~), 女, 硕士研究生, 主要研究方向为地统计模型, E-mail: hanwu1219@163.com

通信作者: 许嘉, E-mail: carol3233@126.com

摘要: 地统计模型被广泛应用于环境空气污染物暴露模拟，但不同建模方法及其模拟结果之间的对比研究较少.基于上海2016~2019年55个环境空气监测点位的NO₂和PM_2.5观测数据，以及交通路网、排放源兴趣点和卫星数据等地统计变量，应用偏最小二乘回归（PLS）、监督学习线性回归（SLR）和机器学习随机森林（RF）这3种建模方法创建年暴露模型，并进一步应用普通克里金插值（OK）法分析模型残差，构建复合模型.应用交叉验证对模型的模拟效果进行检验，选取每一种建模方法的最优模型结构（是否应用OK）作为最终模型.结果表明，NO₂模型中表现最好的是RF-OK（R_mse²为0.70~0.82）和PLS-OK模型（R_mse²为0.78~0.84）；PM_2.5模型中PLS模型（R_mse²为0.62~0.71）优于SLR-OK（R_mse²为0.40~0.79）和RF-OK（R_mse²：0.31~0.56）模型.应用3种建模方法对上海1 km网格开展年暴露模拟和对比，NO₂模型间模拟结果的相关性（r为0.82~0.91）高于PM_2.5模拟结果的相关性（r为0.66~0.96）.基于3种模型2019年的模拟结果，评估了上海NO₂和PM_2.5的人群暴露水平.

关键词: PM_2.5 NO₂ 地统计模型偏最小二乘回归(PLS) 随机森林(RF)

A Comparison Study on Multiple Modeling Approaches for Air Pollutant Geographic Model Development in Shanghai

WU Ying-han¹ , XU Jia¹ , DUAN Yu-sen² , FU Qing-yan² , YANG Wen¹

1. Chinese Research Academy of Environmental Sciences, Beijing 100012, China;
2. Shanghai Environmental Monitoring Center, Shanghai 200235, China

Abstract: Geostatistical models have been widely used in the exposure assessment of ambient air pollutants. However, few studies have focused on comparisons of modeling approaches and their prediction results. Here, we collected the NO₂ and PM_2.5 monitoring data from 55 sites in Shanghai from 2016 to 2019 and the geographic variables, such as road network, points of interest of emission locations, and satellite data were included. We used partial least squares regression (PLS), supervised linear regression (SLR), and random forest (RF) algorithms to develop spatial models and used ordinary kriging (OK) to develop a two-step model. We evaluated the models using a 5-fold cross validation method and selected the best model structure for each modeling approach between one-or two-step models that had been developed with or without OK. The results revealed that the best NO₂ models were the RF-OK (R_mse² was 0.70-0.82) and PLS-OK (R_mse² was 0.78-0.84) models; the PLS model for PM_2.5(R_mse² was 0.62-0.71) outperformed the other PM_2.5 models. We used the best models to predict annual exposures in Shanghai at a 1 km spatial scale and conducted the correlation analysis among the predictions of the best models. The results demonstrated that the NO₂ predictions had higher correlation coefficients (r was 0.82-0.91) compared with those of the PM_2.5 models (r was 0.66-0.96). Based on the exposure results predicted using the three models in 2019, we evaluated the cumulative population exposure concentrations for NO₂ and PM_2.5 in Shanghai.

Key words: PM_2.5 NO₂ geostatistical model partial least squares regression(PLS) random forest(RF)

空气污染能够导致人体的负面健康效应^{[1, 2]}, 应用地统计模型来模拟空气污染物的中长期个体暴露水平, 能够为风险评估和流行病学研究提供数据支撑^{[3, 4]}.

地统计模型中, 土地利用回归模型(land-use regression, LUR)对比Kriging模型精度更高^{[5, 6]}, 应用地统计变量创建的LUR模型被广泛应用于环境空气污染物的个体暴露评估和流行病学研究^{[7, 8]}.在我国天津^[9]、武汉^[10]、南昌^[11]和西安^[12]等城市, 先后应用LUR模型开展了NO₂和PM₁₀等大气污染物的空间分布模拟研究.这些研究基于一定数量固定监测点位(10~13个)的观测数据来创建LUR模型, 在监测点位数量有限的前提下, 通过扩充地统计变量数据库来优化模型^{[13, 14]}.

地统计模型建模方法众多, 但针对不同建模方法及其模拟结果之间开展的对比研究较少.在欧美国家开展的与交通尾气排放相关的大气超细颗粒物^{[15, 16]}和黑碳^[17]地统计模型建模方法研究中发现, 传统的线性回归方法和先进的机器学习算法创建的LUR模型表现相当; 而在针对加州野火的PM_2.5时空模型^[18]和环境PM_2.5组分^[19]的研究中, 机器学习模型比线性回归模型表现更好.Chen等^[20]在欧洲多个城市开展多点位PM_2.5和NO₂的空间模型对比研究, 应用了线性回归、正规化方法和机器学习等16种建模方法建立LUR模型, 发现除神经网络以外, 其他方法建立的PM_2.5和NO₂模型的表现都较好, 但不同模型对地统计变量的敏感性存在差异.

本研究应用变量降维、变量筛选和机器学习在上海创建地统计模型, 开展空间暴露模拟和人群暴露评估的对比研究.

1 材料与方法 1.1 数据来源 1.1.1 环境监测数据

上海是我国的经济、金融、贸易和航运中心, 拥有公路、铁路、水路和航空等多种交通运输方式, 交通排放源种类繁多, 在气象和地理等因素作用下, 空气污染物分布复杂多变.本研究基于上海环境监测网络的55个环境空气监测点位(10个国家监测点位和45个市属监测点位), 开展2016~2019年PM_2.5和NO₂的空间模拟研究.由于站点建设和仪器维护等原因, 市属监测点位观测数据的缺失值较多, 本研究为开展空间暴露模拟研究, 在将日均浓度转化为年均浓度时, 先将空气污染物日均浓度转化为两周平均浓度, 进一步转化为年平均浓度, 数据处理过程中遵循50%有效数据原则.

1.1.2 地统计变量集

本研究收集了人口密度、交通路网(陆路和水路)、与标志区域的距离、兴趣点(point of interest, POI)、土地利用类型、植被指数(normalized difference vegetation index, NDVI)和气溶胶光学厚度(aerosol optical depth, AOD)这7类地统计变量(表 1).考虑到上海交通排放的复杂性, 将陆路交通和水路交通分开作为两类变量.地理数据处理和计算应用QGIS 3.16.11、PostGIS 2.5和PostgreSQL 10软件, 具体计算方法参见表 1和文献^[21].

表 1 地统计变量信息汇总¹⁾ Table 1 Summary of the geostatistical variables

数据类型	变量名称	变量信息描述	半径范围/m	数据来源
人口密度	Population	1 km空间尺度下人口密度	500、1 000、1 500、2 000、2 500、3 000、5 000、10 000和15 000	资源环境科学与数据中心(https://www.resdc.cn/)
交通路网(陆路)	Dist to road A/B/C/D	与道路A、B、C和D的最短距离	50、100、150、200、300、400、500、750、1 000、1 500、3 000和5 000	OpenStreetMap(https://www.openstreetmap.org/)
	Dist to bus route	与公交线路的最短距离
	Dist to inter AA/AB/BB	与交叉路口(道路A与道路A交叉口、道路A与道路B交叉口、道路B与道路B交叉口)的最短距离
	Length of road A/B/C/D	缓冲区内道路A、B、C和D总长度
	Length of bus route	缓冲区内公交线路总长度
交通路网(水路)	Dist to coast	与海岸线的最短距离	50、100、150、200、300、400、500、750、1 000、1 500、3 000和5 000	OpenStreetMap(https://www.openstreetmap.org/)
	Dist to huangpu river	与黄浦江岸的最短距离
	Dist to suzhou river	与苏州河的最短距离
	Dist to yangtze route	与长江的最短距离
	Dist to port huangpu river	与黄浦江港口的最短距离
	Dist to port large	与大型港口的最短距离
	Dist to port other	与其他港口的最短距离
	Length of suzhou river	缓冲区内苏州河总长度
	Length of yangtze route	缓冲区内长江总长度
	Length of huangpu river	缓冲区内黄浦江总长
与标志区域的距离	Dist to airport	与机场的最短距离	—	OpenStreetMap(https://www.openstreetmap.org/)
	Dist to airport large	与大型机场的最短距离
	Dist to airport other	与其他机场的最短距离
	Dist to railway	与铁路的最短距离
	Dist to railyard	与火车站的最短距离
	Dist to temple	与寺庙的最短距离
POI	No. of bus stop	缓冲区内公交车站数量	250、500、1 000、1 500、2 000、2 500、3 000、5 000、7 500、10 000和15 000	OpenStreetMap(https://www.openstreetmap.org/)
	No. of restaurant	缓冲区内餐厅数量
	No.of gas station	缓冲区内加油站数量
	No.of parking	缓冲区内停车场数量
	No.of temple	缓冲区内寺庙数量
	No. of terminal	缓冲区内公交终点站数量
	No.of port	缓冲区内港口数量
	emi PM large	与大型排放源的距离
	emi PM other	与其他排放源的距离
土地利用类型	LU: water	缓冲区内水域面积占比	50、100、150、300、400、500、750、1 000、1 500和3 000	Global land cover 2017(https://data.ess.tsinghua.edu.cn/)
	LU: impersfc	缓冲区内不透水地表面积占比
	LU: barren	缓冲区内裸地面积占比
	LU: forest	缓冲区内森林面积占比
	LU: shrub	缓冲区内灌木林面积占比
	LU: grass	缓冲区内草地面积占比
	LU: crop	缓冲区内耕地面积占比
	LU: wetland	缓冲区内湿地面积占比
植被指数	NDVI: q25	缓冲区内NDVI第25百分位值的平均值	250、500、1 000、2 500和5 000	资源环境科学与数据中心(https://www.resdc.cn/)
	NDVI: q50	缓冲区内NDVI第50百分位值的平均值
	NDVI: q75	缓冲区内NDVI第75百分位值的平均值
	NDVI: summer	缓冲区内4~9月NDVI第50百分位值的平均值
	NDVI: winter	缓冲区内1~3月、10~12月NDVI第50百分位值的平均值
气溶胶光学厚度	AOD	AOD的平均值	250、500、1 000、2 500和5 000	NASA-EARTHDATA(https://lpdaac.usgs.gov/products/mcd19a2v006/)
	AOD: cold	1~3月、10~12月AOD的平均值
	AOD: warm	4~9月AOD的平均值
1)道路A、B、C和D分别表示快速路、主干道、次干道和支路

表 1 地统计变量信息汇总¹⁾ Table 1 Summary of the geostatistical variables

1.2 建模方法

本研究应用偏最小二乘回归法(partial least squares regression, PLS)、监督学习线性回归(supervised linear regression, SLR)和随机森林(random forest, RF)这3种方法创建模型, 它们分别代表变量降维、变量筛选和机器学习这3种模型类型.应用R(version 3.4.0)统计分析平台、“pls”和“randomForest”等R工具包创建模型.

1.2.1 PLS

PLS回归方法是一种寻求响应变量和自变量之间协方差最大化, 将自变量矩阵分解为因子载荷和因子得分矩阵的数据降维方法^[22].本研究以污染物年均浓度为响应变量, 以地统计变量集为自变量, 应用降维后的PLS因子得分矩阵为自变量创建LUR模型时.根据以往研究经验, 将因子数量设定为3个^{[23, 24]}.

1.2.2 SLR

SLR是一种以筛选后的地统计变量作为自变量的前向逐步回归建模方法.变量筛选步骤包括: ①将因变量与各地统计变量逐个进行回归分析, 筛选出R²最高且回归系数与预设方向(正或负)相同的地统计变量, 作为自变量纳入线性回归模型; ②对剩余地统计变量重复步骤①, 直到线性回归模型的R²增加值小于0.01; ③应用方差膨胀因子(variance inflation factor, VIF)对所筛选变量的共线性进行检验, 去除VIF大于3的变量^{[3, 25]}; ④将经纬度相关变量(lambert x, lambert y, x plus y, x minus y)作为强制变量纳入模型.其中, lambert x、lambert y、x plus y和x minus y分别为兰伯特投影下点位的经度、纬度、经纬度之和以及经纬度之差.最后, 应用筛选出的地统计变量创建SLR模型.

1.2.3 RF

RF是一种基于决策树的集成学习算法, 属于机器学习的一种.在应用RF构建LUR模型时, 强制分割潜在预测变量为m个子集, 并对每个子集单独训练一棵决策树, 将决策树模拟结果的平均值作为随机森林的模拟结果^[26].RF应用重要性评价指标(increase in mean squared error, IncMSE)评估自变量的重要性, 通过IncMSE来判断各自变量对模型模拟结果的影响^[27].本次研究中, 设置mtry(随机抽样的变量个数)、ntree(随机森林所包含的决策树数目)和nodesize(决策树节点的最小个数)参数分别为50、750和5^[28].

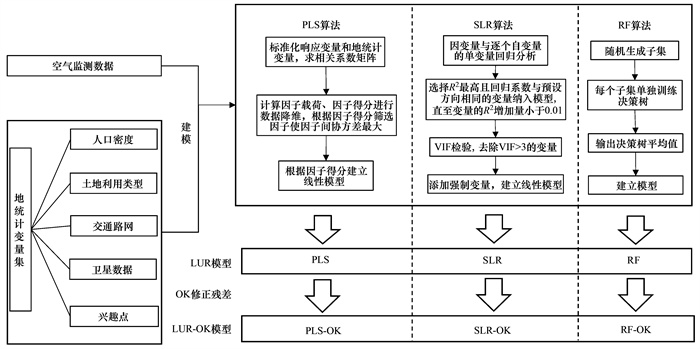
1.2.4 模型结构

本研究应用3种建模方法建立LUR模型后, 进一步将LUR模型残差作为因变量, 应用普通克里金插值法(ordinary kriging, OK)创建LUR-OK复合结构模型^{[20, 29, 30]}, 模型建立流程如图 1所示.对每一种建模方法而言, 比较LUR和LUR-OK模型, 为每种建模方法选取最优模型结构.

图 1 模型建立流程示意 Fig. 1 Methodology of LUR model development

1.3 模型验证

应用5倍交叉验证(cross-validation, CV)来检验模型的精确度和准确度.将数据集随机分为5部分, 其中4部分数据作为模拟组, 用来创建模型; 剩余一部分作为验证组; 依次进行5次模拟和验证后得到CV模拟结果.应用均方误差决定系数(mean square error based-R², R_mse²)、线性回归决定系数(regression based-R², R_reg²)和均方根误差(root mean squared error, RMSE)来表征模型的模拟效果, RMSE和R_mse²的计算方法如式(1)和式(2)所示.在将模型模拟结果和观测数据进行比较时, R_mse²反映的是观测值与CV模拟值同1:1直线的对比效果, 能更直接地反映模型模拟效果, 因此将R_mse²作为模型的主要验证指标.

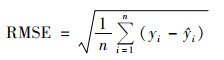
(1)

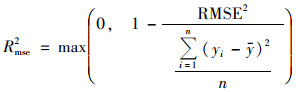
(2)

式中, y_i为第i个样本的观测值; _i为第i个样本的模拟结果; 为模拟结果的平均值; n为样本数量.

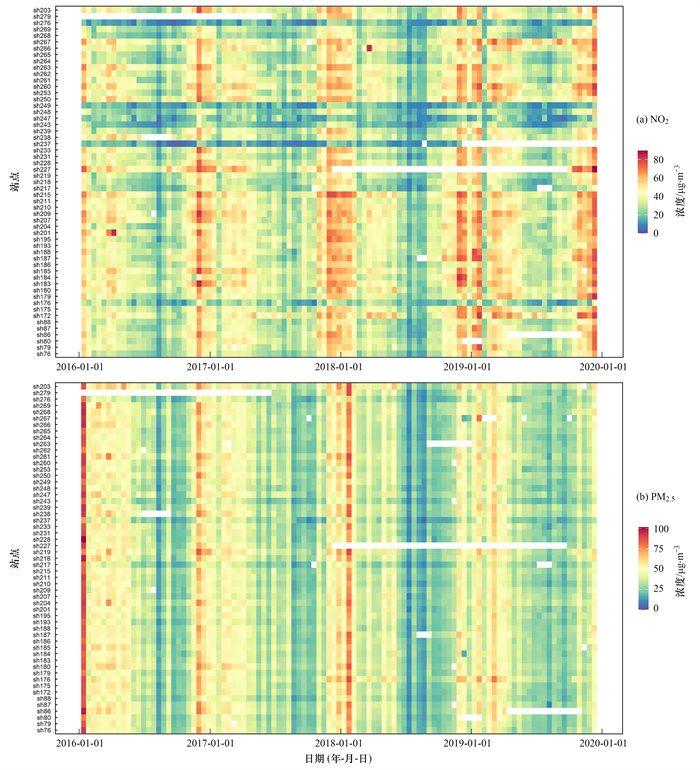
2 结果与讨论 2.1 NO₂和PM_2.5年均值

图 2是上海55个环境空气监测点位的两周浓度平均值.由图 2所示, NO₂的空间变异较大, 未呈现出明显的时间变化趋势; 而PM_2.5的空间变异较小, 其呈现逐年降低的时间变化趋势.在计算NO₂和PM_2.5的年均值时, 考虑季节性缺失对年均值的影响, 按照大于75%有效数据的原则计算年均值.表 2总结了2016~2019年NO₂和PM_2.5的年均值和有效点位数量, 其中, 参与NO₂模型建模的点位有52~54个, 参与PM_2.5模型建模的点位有53~54个.

图 2 上海55个环境空气监测点位NO₂和PM_2.5的两周浓度平均值的时空分布 Fig. 2 Spatio-temporal distribution of the two-week average concentrations of NO₂ and PM_2.5 at the 55 monitoring sites in Shanghai

表 2 2016~2019年NO₂和PM_2.5年均浓度和有效数据统计数据 Table 2 Statistics of annual average concentration and effective data of NO₂ and PM_2.5 from 2016 to 2019

2.2 模型参数和敏感性分析 2.2.1 PLS模型

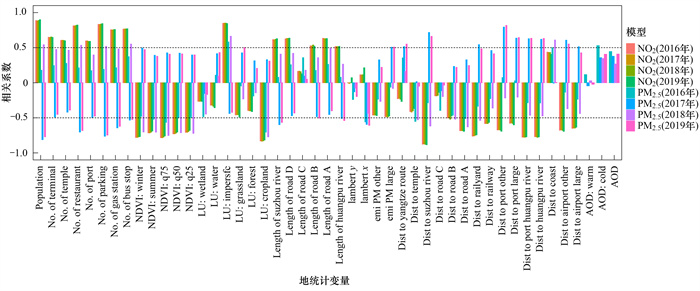
将年均浓度作为响应变量, 应用PLS方法对地统计变量集降维后得到3个因子.对NO₂而言, 2016~2019年第一个PLS因子解释了51% ~60%的NO₂年均浓度和45% ~47%的地统计变量集; PM_2.5模型的第一个PLS因子解释了25% ~50%的PM_2.5年均浓度和13% ~35%的地统计变量集.第一个因子在PLS模型中作为自变量, 解释了大部分地统计变量集, 因此用第一个PLS因子和地统计变量的相关系数来表征PLS模型中各个地统计变量的敏感性, 如图 3所示.其中, 每一列表示一类地统计变量和第一个PLS因子的相关系数, 其中对于具有多个缓冲半径的地统计变量, 柱状图表示全部缓冲半径的相关系数均值, 变量信息见表 1.由图 3可知, 对于同一地统计变量, 2016~2019年4个NO₂模型的第一个PLS因子较稳定, 相关系数变化不明显; 而不同年均值下PM_2.5模型的第一个PLS因子与同一地统计变量间的相关系数变化较大, 其中POI数量(餐厅、停车场和加油站等)、土地利用类型(作物和草地等)和NDVI变量的相关系数在年均值模型中出现正负值的差异, 这一部分差异由第二个PLS因子来进一步解释(第二个因子解释了17% ~38%的地统计变量集).

图 3 第一个PLS因子与地统计变量的相关系数 Fig. 3 Correlation coefficients between the first PLS score and the corresponding geographic variables

PM_2.5和NO₂的PLS模型中, 对其年均浓度值模拟影响最大的地统计变量包括陆路交通(道路长度和与道路的距离等)、水路交通(与港口的距离和与河流的距离等)、POI数量(餐厅、停车场和加油站等)、土地利用类型(作物和草地等)、NDVI和人口密度, 以上地统计变量与PLS第一因子相关系数的绝对值都大于0.5, 与本课题组在上海和北京的研究结果相符^{[21, 23, 24]}.

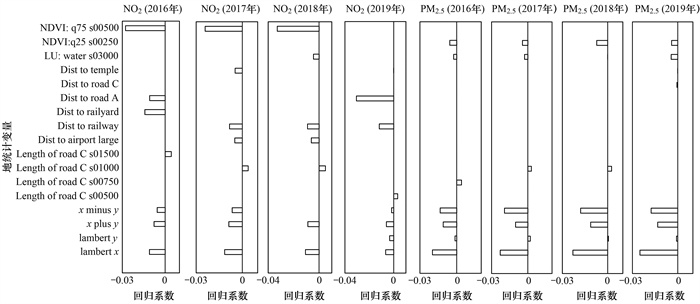
2.2.2 SLR模型

为使不同自变量间的回归系数具有可比性, 本研究将每一个自变量系数乘以其对应的归一化因子(自变量第95百分位和第5百分位间的差值与因变量第95百分位和第5百分位间的差值的比值)^[31].图 4是SLR模型筛选出的地统计变量及其归一化后的回归系数.SLR模型结果表明, NO₂的浓度与NDVI(第75百分位500 m缓冲区)呈高度负相关(回归系数为-0.033~-0.024); NO₂受主干道、火车站和铁路的影响较大(回归系数为-0.031~-0.005).道路长度与NO₂浓度呈正相关(回归系数为0.004~0.005).本研究发现机场和寺庙区域对上海NO₂的影响不容忽视(回归系数为-0.006~-0.005), 同香港^{[32, 33]}、天津^[34]、武汉^[35]和北京^[36]等多个城市的研究结论相符, 寺庙中的燃香行为、飞机起飞和着陆时的尾气排放均会对城市NO₂产生影响.PM_2.5浓度与经度呈高度负相关(回归系数为-0.025~-0.020), 与NDVI、与寺庙的距离、与道路的距离和缓冲区内水面面积呈负相关(回归系数为-0.007~-0.001), 与缓冲区内道路总长度呈正相关(回归系数为0.003~0.004).本研究发现地理位置、陆路交通和土地利用类型对上海PM_2.5的影响较大, 同广州^[37]研究结论相符.

s00250、s00500、s00750、s01000、s01500和s03000表示缓冲区半径, 下同图 4 SLR模型预测变量筛选结果及变量回归系数 Fig. 4 Variables predicted by the result of the SLR model and their regression coefficients

为评估经纬度对SLR模型的影响, 剔除经纬度变量后重新建模, 2016~2019年NO₂和PM_2.5的SLR模型的交叉验证R_mse²的结果分别为0.54~0.71和0.41~0.67.同有经纬度变量的SLR模型相比, NO₂模型R_mse²变化了-2% ~3%, 其中2018年模型变化最大, 为3%; PM_2.5模型R_mse²下降了-10% ~40%, 其中2017年模型变化最大, 为40%; 2018年次之, 为31%, 这表明经纬度变量对PM_2.5 SLR模型的影响较大, 由图 4可知, 经度变量比纬度对PM_2.5的影响更大, 表明PM_2.5在经度方向上的变化更明显, 这与以往研究的结论相符^[38].

综上所述, NO₂的2016~2019年SLR模型筛选出的地统计变量差异较大, 并且同一地统计变量的在不同年份的模型中回归系数大小差别较大; 与NO₂模型相比, PM_2.5的2016~2019年SLR模型筛选出的变量种类和模型回归系数的大小较为一致.

2.2.3 RF模型

图 5汇总了NO₂和PM_2.5的RF模型中IncMSE排名前10的变量.对NO₂贡献较大的变量包括公路交通(道路长度、与铁路的距离)、水路交通(与港口的距离、与河流的距离)、与排放源(火车站)的距离、POI数量(公交站点、餐厅、停车场)、土地利用类型(草地、硬化地面)和人口密度, 其中贡献最大的地统计变量是与火车站的距离, 其IncMSE达到16%; 公交站点POI数量的IncMSE在7% ~11%之间, 人口密度的IncMSE在4% ~11%之间, 水路交通(与港口的距离和与河流的距离)的IncMSE在4% ~14%之间, 说明上海铁路轨道交通、水路交通对NO₂浓度的影响较大.

图 5 RF模型中地统计变量的IncMSE Fig. 5 Increase in the mean squared error (IncMSE) of the geographic variables for RF models

对PM_2.5的空间变化影响较大的地统计变量包括: 经度变量、土地利用类型(湿地)、水路交通(与港口的距离、与河流的距离)、POI(餐厅、加油站)数量和人口密度.其中, 经度变量的IncMSE最大, 在2% ~7%之间; 其他变量的IncMSE在1% ~2%之间.本研究中, 上海PM_2.5的空间分布受经度的影响最大, 这与SLR模型结果相似.

Brokamp等^[19]的PM_2.5空间模拟研究发现, RF模型的模拟效果与训练数据集数量、观测数据的变异度、数据中关系的复杂性有关.NO₂的RF模型具有高IncMSE值的地统计变量在2016~2019年之间存在较大差异, 而在PM_2.5各年均值模型中, 具有高IncMSE值的地统计变量类似, 这与本研究SLR模型筛选出的变量较为一致.这可能与NO₂各年纳入RF模型的点位数量和位置不同有关(表 2), NO₂的空间变化较大, 点位数量和位置影响RF模型的结果.

2.3 模型验证和最优模型结构

2016~2019年两种模型结构(LUR和LUR-OK)的PLS、SLR和RF模型5倍交叉验证结果如表 3所示.通过交叉验证结果, 选取NO₂和PM_2.5在3种建模方法的最优模型结构, 除PM_2.5的PLS模型以外, 其他建模方法的最优模型结构均为LUR-OK.对NO₂而言, PLS-OK、SLR-OK和RF-OK模型R_mse²在0.59~0.84之间, RMSE在3.1~5.7之间, 增加OK的LUR-OK模型结构使3种模型的R_mse²提高了0.01~0.07, RMSE降低了0.1~0.6.PM_2.5的SLR-OK和RF-OK模型R_mse²在0.31~0.79之间, RMSE在1.8~2.7之间, 其中PM_2.52016年和2017年SLR-OK模型的R_mse²比SLR模型分别提高了11%和18%; PM_2.5的RF-OK模型R_mse²提高了55% ~143%, RMSE降低了7% ~22%.由此表明, LUR-OK模型结构可进一步解释空气污染物的空间分布, 从而有效提升模型精确度和准确度.

表 3 模型交叉验证结果¹⁾ Table 3 Comparison of cross-validation results of the models

污染物	年份	PLS			SLR			RF
污染物	年份	RMSE	R_mse²	R_reg²	RMSE	R_mse²	R_reg²	RMSE	R_mse²	R_reg²
NO₂	2016	3.7	0.81	0.8	5.0	0.67	0.7	5.3	0.63	0.6
	2017	3.7	0.79	0.8	5.5	0.54	0.6	4.4	0.71	0.7
	2018	3.5	0.80	0.8	4.2	0.71	0.7	3.7	0.77	0.8
	2019	4.4	0.77	0.8	5.7	0.61	0.6	5.1	0.70	0.7
PM_2.5	2016	2.2	0.71	0.8	2.3	0.67	0.7	3.2	0.35	0.3
	2017	1.7	0.71	0.7	2.0	0.57	0.6	2.8	0.21	0.4
	2018	1.9	0.62	0.7	2.1	0.54	0.5	2.8	0.20	0.4
	2019	1.6	0.69	0.7	2.2	0.41	0.4	2.2	0.39	0.2

污染物	年份	PLS-OK			SLR-OK			RF-OK
污染物	年份	RMSE	R_mse²	R_reg²	RMSE	R_mse²	R_reg²	RMSE	R_mse²	R_reg²
NO₂	2016	3.6	0.83	0.8	4.7	0.71	0.7	4.7	0.70	0.7
	2017	3.6	0.80	0.8	5.2	0.59	0.6	4.2	0.73	0.7
	2018	3.1	0.84	0.8	4.0	0.73	0.8	3.3	0.82	0.8
	2019	4.3	0.78	0.8	5.7	0.61	0.6	4.7	0.74	0.7
PM_2.5	2016	2.3	0.66	0.8	1.8	0.79	0.8	2.7	0.56	0.6
	2017	1.7	0.68	0.7	1.9	0.63	0.6	2.2	0.51	0.6
	2018	2.0	0.60	0.7	2.3	0.48	0.5	2.6	0.31	0.6
	2019	1.7	0.66	0.7	2.2	0.40	0.4	2.2	0.39	0.5
1)黑体字表示每种建模方法的最优模型结构

表 3 模型交叉验证结果¹⁾ Table 3 Comparison of cross-validation results of the models

NO₂模型的R_mse²普遍高于PM_2.5模型, 由于NO₂主要来源于交通排放, 由PLS模型中地统计变量与第一个PLS因子相关性(图 3)、SLR和RF模型的最重要变量类型(图 4和图 5)可以看出, 与NO₂相关的交通排放不仅包括道路, 还有水路和轨道交通排放, 以往研究也得到过类似结论^{[24, 39]}.对于不同建模方法而言, 其最优模型结构存在差异, SLR和RF的最优模型结构是LUR-OK; 而NO₂的PLS-OK模型与PLS模型相比, 只明显优化了NO₂模型的交叉验证结果, 说明在PLS的PM_2.5模型已经通过地统计变量集较好地解释了空间变化.

本研究将5倍交叉验证结果作为模型精确度和准确度的判断依据.由于随机分组的数量不同, 可能导致交叉验证结果存在差异, 本研究还使用10倍交叉验证方法来评估模型模拟效果, 结果表明10倍交叉验证的R_mse²未出现明显变化.此外, 本研究还应用莫兰指数检测模型残差的空间自相关性^[40], 所有模型的莫兰指数都接近于0, 结果表明模型残差没有明显的空间自相关, 满足其空间独立性假设, 说明模型较可靠.

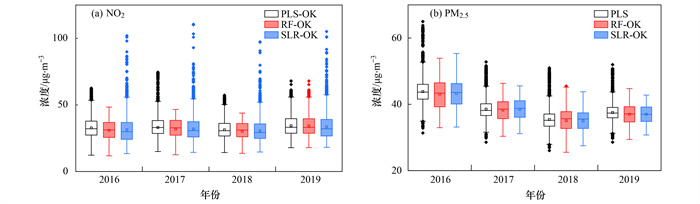
2.4 模型模拟

本研究应用PLS-OK、SLR-OK和RF-OK模型模拟了NO₂在上海的空间分布; 用PLS、SLR-OK和RF-OK模型模拟了PM_2.5的空间分布.受地统计变量覆盖范围的限制, 上海被划分为6 195个1 km空间分辨率网格, 每个网格中心点的污染物模拟结果代表该网格内的人群暴露浓度.图 6是2016~2019年NO₂和PM_2.5的网格模拟结果, 对NO₂而言, 所有模型的模拟均值在30.2~34.3 μg ·m^-3之间, 25% ~75%区间模拟结果较一致, SLR-OK的模拟结果在5% ~95%区间以外的极端值点明显多于PLS-OK和RF-OK的模拟结果; PM_2.5所有模型的模拟结果均值范围为35.0~43.9 μg ·m^-3之间, 与NO₂模拟结果相比, PM_2.5模拟值25% ~75%区间差异较大, PLS模拟结果的极端值点对比RF-OK和SLR-OK模拟结果较多.

箱式图中矩形内圆点表示均值; 矩形由下至上3条横线分别表示25%、50%和75%分位数; 上下两条短线分别表示95%和5%置信区间; 短线以外的圆点表示极值图 6 污染物浓度模型模拟值 Fig. 6 Predicted value of pollutant concentrations by the best models

本研究对2016~2019年3种模型的模拟结果开展相关性分析.对NO₂而言, 每一类模型在2016~2019年模拟结果的皮尔森相关性系数(Pearson correlation coefficient, r)在0.84~0.99之间, 其中, PLS-OK(r: 0.94~0.98)和RF-OK模型(r: 0.97~0.99)模拟结果的相关性较高; 而SLR-OK模型模拟结果相关性较低(r: 0.84~0.98), 其中2017年与2019年相关性最低, 说明各年份监测点位数量、数据缺失率的变化可能对SLR-OK模型产生影响.与NO₂相比, PM_2.5各年度模型模拟结果的相关系数在0.90~0.97之间, 说明PM_2.5模型受监测点位变化的影响较小.此外, 本研究还对同一年份的3种模型的模拟结果之间进行相关性分析.NO₂于3种模型(PLS-OK、SLR-OK和RF-OK)的模拟结果相关性较强(r为0.82~0.91), 其中PLS-OK模型与SLR-OK模型之间相关性最好, r可达到0.91.PM_2.5在3种模型(PLS、SLR-OK和RF-OK)模拟结果间的相关系数在0.66~0.96之间, 其中RF-OK模型与SLR-OK模型相关性较强(r为0.90~0.96), 这与二者主要通过OK来解释PM_2.5的空间分布有关.总体而言, 对同一种污染物而言, 3种模型的模拟结果都很稳定, 不同模型的模拟结果拟合度高, 模型适应性强.

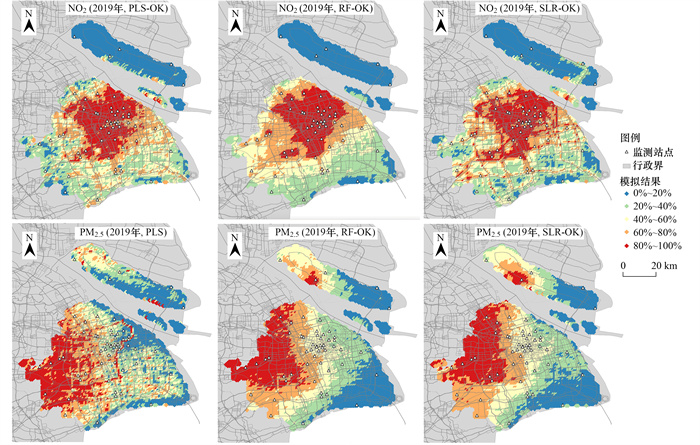
2.5 人群暴露模拟

图 7是2019年上海NO₂和PM_2.5的1 km×1 km网格的暴露模拟地图.NO₂浓度呈现由市中心向市郊逐渐降低的空间分布趋势, 其中高浓度热点与路网的空间分布一致; 而PM_2.5浓度呈现西高东低的变化趋势.对比3种模型的模拟地图发现, 虽然NO₂的RF-OK模型的交叉验证结果与SLR-OK和PLS-OK较接近(表 3), 但模拟地图呈现出较大的空间差异.对PM_2.5而言, RF-OK模型与SLR-OK模型的空间变化趋势较一致, 而PLS模型与RF-OK模型、SLR-OK模型的交叉验证结果相比差异较大的同时, 模拟地图的空间差异也较大.

图 7 上海NO₂和PM_2.5的模拟结果 Fig. 7 Prediction maps for NO₂ and PM_2.5 in Shanghai

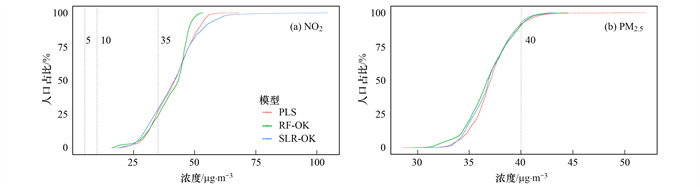
基于3种模型的模拟结果和人口分布密度, 本研究进一步评估了NO₂和PM_2.5的累积人群暴露浓度, 如图 8所示.NO₂的年均暴露浓度达到环境空气质量二级标准(年均暴露浓度低于40 μg ·m^-3)的人群占40% ~46%.NO₂在3种模型的低暴露(暴露浓度符合环境空气质量二级标准)模拟结果较一致, 而高暴露模拟结果差异较大, RF-OK的高暴露模拟结果显著高于其他两个模型.3种PM_2.5模型的模拟结果较一致, 其中PM_2.5年均暴露浓度达到环境空气质量二级标准(年均暴露浓度低于35 μg ·m^-3)的人口占比为14% ~19%.同世界卫生组织(WHO)提出的全球空气质量指导值(AQG2005为10 μg ·m^-3, AQG2021为5 μg ·m^-3)相比, 上海地区人群的PM_2.5暴露浓度较高^[41], 高PM_2.5暴露可能导致人群的多种健康效应和相应疾病负担^[42~44], 需得到关注.综上所述, 上海NO₂的高暴露人群远多于PM_2.5的高暴露人群, 在PM_2.5得到有效控制后其浓度逐年降低的情况下, NO₂的高暴露水平仍需得到重视.

虚线为WHO提出的全球空气质量指导值图 8 2019年上海人群暴露于NO₂和PM_2.5的累积分布 Fig. 8 Cumulative distribution of NO₂ exposure and PM_2.5 exposure in Shanghai urban population in 2019

3 结论

本研究在上海应用PLS、SLR和RF这3种建模方法并分别结合OK创建了NO₂和PM_2.5的2016~2019年的空间分布模型, 根据交叉验证结果得到NO₂的最优结构模型是PLS-OK、SLR-OK和RF-OK, PM_2.5的最优结构模型是PLS、SLR-OK和RF-OK.NO₂模型中RF-OK(R_mse²为0.70~0.82)和PLS-OK模型(R_mse²为0.78~0.84)的表现最好; PM_2.5模型中PLS模型(R_mse²为0.62~0.71)明显优于SLR-OK(R_mse²为0.40~0.79)和RF-OK(R_mse²为0.31~0.56)模型.对3种最优结构模型在上海地区的年均值模拟结果和人群暴露评估进行比较研究发现, 交叉验证结果相近的模型, 其空间模拟结果存在差异, 这体现出应用空间模拟结果结合交叉验证结果综合评估和对比不同模型表现的重要性.

致谢: 感谢国家环境保护长三角区域大气复合污染上海淀山湖科学观测研究站(State-Ecologyand Environment Scientific Observation and Research Station for the Yangtze River Delta at Dianshan Lake)对本研究的支持.

参考文献

[1]	Lo K, Chiang L L, Hsu S M, et al. Association of short-term exposure to air pollution with depression in patients with sleep-related breathing disorders[J]. Science of the Total Environment, 2021, 786. DOI:10.1016/j.scitotenv.2021.147291
[2]	Liu S, Lim Y H, Pedersen M, et al. Long-term exposure to ambient air pollution and road traffic noise and asthma incidence in adults: the Danish Nurse cohort[J]. Environment International, 2021, 152. DOI:10.1016/j.envint.2021.106464
[3]	Eeftens M, Tsai M Y, Ampe C, et al. Spatial variation of PM_2.5, PM₁₀, PM_2.5absorbance and PM_coarse concentrations between and within 20 European study areas and the relationship with NO₂-Results of the ESCAPE project[J]. Atmospheric Environment, 2012, 62: 303-317. DOI:10.1016/j.atmosenv.2012.08.038
[4]	Beelen R, Hoek G, Vienneau D, et al. Development of NO₂ and NO_x land use regression models for estimating air pollution exposure in 36 study areas in Europe-The ESCAPE project[J]. Atmospheric Environment, 2013, 72: 10-23. DOI:10.1016/j.atmosenv.2013.02.037
[5]	李沈鑫, 邹滨, 刘兴权, 等. 2013-2015年中国PM_2.5污染状况时空变化[J]. 环境科学研究, 2017, 30(5): 678-687. Li S X, Zou B, Liu X Q, et al. Pollution status and spatial-temporal variations of PM_2.5 in China during 2013-2015[J]. Research of Environmental Sciences, 2017, 30(5): 678-687.
[6]	刘炳杰, 彭晓敏, 李继红. 基于LUR模型的中国PM_2.5时空变化分析[J]. 环境科学, 2018, 39(12): 5296-5307. Liu B J, Peng X M, Li J H. Analysis of the temporal and spatial variation of PM_2.5 in China based on the LUR model[J]. Environmental Science, 2018, 39(12): 5296-5307.
[7]	Brauer M, Lencar C, Tamburic L, et al. A cohort study of traffic-related air pollution impacts on birth outcomes[J]. Environmental Health Perspectives, 2008, 116(5): 680-686. DOI:10.1289/ehp.10952
[8]	Pedersen M, Giorgis-Allemand L, Bernard C, et al. Ambient air pollution and low birthweight: a European cohort study (ESCAPE)[J]. The Lancet Respiratory Medicine, 2013, 1(9): 695-704. DOI:10.1016/S2213-2600(13)70192-9
[9]	陈莉, 白志鹏, 苏笛, 等. 利用LUR模型模拟天津市大气污染物浓度的空间分布[J]. 中国环境科学, 2009, 29(7): 685-691. Chen L, Bai Z P, Su D, et al. Application of land use regression to simulate ambient air PM₁₀to and NO₂ concentration in Tianjin City[J]. China Environmental Science, 2009, 29(7): 685-691.
[10]	刘阳红, 李浪姣, 王伟业. 基于LUR构建武汉市NO₂暴露浓度预测模型[J]. 廊坊师范学院学报(自然科学版), 2018, 18(4): 66-69. Liu Y H, Li L J, Wang W Y. Application of LUR for constructing the prediction model of NO₂ exposure concentration in Wuhan[J]. Journal of Langfang Normal University (Natural Science Edition), 2018, 18(4): 66-69.
[11]	梁照凤, 陈文波, 郑蕉, 等. 南昌市中心城区主要大气污染物分布模拟及土地利用对其影响[J]. 应用生态学报, 2019, 30(3): 1005-1014. Liang Z F, Chen W B, Zheng J, et al. Simulation of the distribution of main atmospheric pollutants and the influence of land use on them in central urban area of Nanchang City, China[J]. Chinese Journal of Applied Ecology, 2019, 30(3): 1005-1014.
[12]	贺佳, 贺亮, 张涛, 等. 基于GIS和LUR模型的西安市PM_2.5浓度空间分布模拟研究[J]. 环境科学与管理, 2017, 42(2): 57-60. He J, He L, Zhang T, et al. Simulation study on spatial distribution of PM_2.5 concentration in Xi'an based on GIS and LUR model[J]. Environmental Science and Management, 2017, 42(2): 57-60.
[13]	焦利民, 许刚, 赵素丽, 等. 基于LUR的武汉市PM_2.5浓度空间分布模拟[J]. 武汉大学学报(信息科学版), 2015, 40(8): 1088-1094. Jiao L M, Xu G, Zhao S L, et al. LUR-based Simulation of the Spatial Distribution of PM_2.5 of Wuhan[J]. Geomatics and Information Science of Wuhan University, 2015, 40(8): 1088-1094.
[14]	吴健生, 廖星, 彭建, 等. 重庆市PM_2.5浓度空间分异模拟及影响因子[J]. 环境科学, 2015, 36(3): 759-767. Wu J S, Liao X, Peng J, et al. Simulation and influencing factors of spatial distribution of PM_2.5 concentrations in Chongqing[J]. Environmental Science, 2015, 36(3): 759-767.
[15]	Kerckhoffs J, Hoek G, Portengen L, et al. Performance of prediction algorithms for modeling outdoor air pollution spatial surfaces[J]. Environmental Science & Technology, 2019, 53(3): 1413-1421.
[16]	Weichenthal S, van Ryswyk K, Goldstein A, et al. A land use regression model for ambient ultrafine particles in Montreal, Canada: a comparison of linear regression and a machine learning approach[J]. Environmental Research, 2016, 146: 65-72. DOI:10.1016/j.envres.2015.12.016
[17]	van den Bossche J, de Baets B, Verwaeren J, et al. Development and evaluation of land use regression models for black carbon based on bicycle and pedestrian measurements in the urban environment[J]. Environmental Modelling & Software, 2018, 99: 58-69.
[18]	Reid C E, Jerrett M, Petersen M L, et al. Spatiotemporal prediction of fine particulate matter during the 2008 northern California wildfires using machine learning[J]. Environmental Science & Technology, 2015, 49(6): 3887-3896.
[19]	Brokamp C, Jandarov R, Rao M B, et al. Exposure assessment models for elemental components of particulate matter in an urban environment: a comparison of regression and random forest approaches[J]. Atmospheric Environment, 2017, 151: 1-11. DOI:10.1016/j.atmosenv.2016.11.066
[20]	Chen J, de Hoogh K, Gulliver J, et al. A comparison of linear regression, regularization, and machine learning algorithms to develop Europe-wide spatial models of fine particles and nitrogen dioxide[J]. Environment International, 2019, 130. DOI:10.1016/j.envint.2019.104934
[21]	Xu J, Yang Z C, Han B, et al. A unified empirical modeling approach for particulate matter and NO₂ in a coastal city in China[J]. Chemosphere, 2022, 299. DOI:10.1016/j.chemosphere.2022.134384
[22]	Keller J P, Olives C, Kim S Y, et al. A unified spatiotemporal modeling approach for predicting concentrations of multiple air pollutants in the multi-ethnic study of atherosclerosis and air pollution[J]. Environmental Health Perspectives, 2015, 123(4): 301-309. DOI:10.1289/ehp.1408145
[23]	Xu J, Yang W, Han B, et al. An advanced spatio-temporal model for particulate matter and gaseous pollutants in Beijing, China[J]. Atmospheric Environment, 2019, 211: 120-127. DOI:10.1016/j.atmosenv.2019.04.011
[24]	Xu J, Yang W, Bai Z P, et al. Modeling spatial variation of gaseous air pollutants and particulate matters in a Metropolitan area using mobile monitoring data[J]. Environmental Research, 2022, 210. DOI:10.1016/j.envres.2022.112858
[25]	Eeftens M, Beelen R, de Hoogh K, et al. Development of land use regression models for PM_2.5, PM_2.5 absorbance, PM₁₀ and PM_coarse in 20 European study areas; results of the ESCAPE project[J]. Environmental Science & Technology, 2012, 46(20): 11195-11205.
[26]	Araki S, Shima M, Yamamoto K. Spatiotemporal land use random forest model for estimating metropolitan NO₂ exposure in Japan[J]. Science of the Total Environment, 2018, 634: 1269-1277. DOI:10.1016/j.scitotenv.2018.03.324
[27]	张志豪, 陈楠, 祝波, 等. 基于随机森林模型的武汉市城区大气PM_2.5来源解析[J]. 环境科学, 2022, 43(3): 1151-1158. Zhang Z H, Chen N, Zhu B, et al. Source analysis of ambient PM_2.5 in Wuhan City based on random forest model[J]. Environmental Science, 2022, 43(3): 1151-1158.
[28]	王鹏, 赵鑫涯, 宋珂. 基于随机森林算法的长江三角洲地区PM_2.5浓度模拟研究[J]. 中国环境监测, 2021, 37(5): 21-31. Wang P, Zhao X Y, Song K. Prediction of PM_2.5 concentration in yangtze river delta based on random forest algorithm[J]. Environmental Monitoring in China, 2021, 37(5): 21-31.
[29]	Meng X, Chen L, Cai J, et al. A land use regression model for estimating the NO₂ concentration in Shanghai, China[J]. Environmental Research, 2015, 137: 308-315. DOI:10.1016/j.envres.2015.01.003
[30]	de Hoogh K, Chen J, Gulliver J, et al. Spatial PM_2.5, NO₂, O₃and BC models for Western Europe-Evaluation of spatiotemporal stability[J]. Environment International, 2018, 120: 81-92. DOI:10.1016/j.envint.2018.07.036
[31]	Hankey S, Marshall J D. Land use regression models of on-road particulate air pollution (particle number, black carbon, PM_2.5, particle size) using mobile monitoring[J]. Environmental Science & Technology, 2015, 49(15): 9194-9202.
[32]	郑子豪, 吴志峰, 陈颖彪, 等. 基于Sentinel-5P的粤港澳大湾区NO₂污染物时空变化分析[J]. 中国环境科学, 2021, 41(1): 63-72. Zheng Z H, Wu Z F, Chen Y B, et al. Analysis of temporal and spatial variation characteristics of NO₂ pollutants in Guangdong-Hong Kong-Macao Greater Bay Area based on Sentinel-5P satellite data[J]. China Environmental Science, 2021, 41(1): 63-72. DOI:10.3969/j.issn.1000-6923.2021.01.008
[33]	Wang B, Lee S C, Ho K F, et al. Characteristics of emissions of air pollutants from burning of incense in temples, Hong Kong[J]. Science of the Total Environment, 2007, 377(1): 52-60. DOI:10.1016/j.scitotenv.2007.01.099
[34]	韩博, 姚婷玮, 王立婕, 等. 天津机场区域大气NO₂及O₃影响因子研究[J]. 中国环境科学, 2020, 40(6): 2398-2408. Han B, Yao T W, Wang L J, et al. Study on influencing factors of atmospheric NO₂ and O₃ in Tianjin Binhai international airport[J]. China Environmental Science, 2020, 40(6): 2398-2408.
[35]	施媛媛, 李仁东, 邱娟, 等. 基于LUR的二氧化氮浓度空间分布模拟及其下垫面影响因素分析[J]. 地球信息科学学报, 2017, 19(1): 10-19. Shi Y Y, Li R D, Qiu J, et al. Spatial distribution simulation and underlying surface factors analysis of NO₂ concentration based on land use regression[J]. Journal of Geo-information Science, 2017, 19(1): 10-19.
[36]	Xue Y F, Cao X Z, Ai Y, et al. Primary air pollutants emissions variation characteristics and future control strategies for transportation sector in Beijing, China[J]. Sustainability, 2020, 12(10). DOI:10.3390/su12104111
[37]	Mo Y Z, Booker D, Zhoa S Z, et al. The application of land use regression model to investigate spatiotemporal variations of PM_2.5in Guangzhou, China: Implications for the public health benefits of PM_2.5 reduction[J]. Science of the Total Environment, 2021, 778. DOI:10.1016/j.scitotenv.2021.146305
[38]	陈杨欢, 王杨君, 张苗云, 等. 上海市大气PM_2.5时空分布特征[J]. 环境工程学报, 2017, 11(6): 3671-3677. Chen Y H, Wang Y J, Zhang M Y, et al. Temporal and spatial distribution of PM_2.5 in Shanghai based on clustering analysis[J]. Chinese Journal of Environmental Engineering, 2017, 11(6): 3671-3677.
[39]	de Hoogh K, Gulliver J, van Donkelaar A, et al. Development of West-European PM_2.5 and NO₂land use regression models incorporating satellite-derived and chemical transport modelling data[J]. Environmental Research, 2016, 151: 1-10. DOI:10.1016/j.envres.2016.07.005
[40]	陈彦光. 基于Moran统计量的空间自相关理论发展和方法改进[J]. 地理研究, 2009, 28(6): 1449-1463. Chen Y G. Reconstructing the mathematical process of spatial autocorrelation based on Moran's statistics[J]. Geographical Research, 2009, 28(6): 1449-1463.
[41]	Wang H, Li J W, Gao Z Q, et al. High-spatial-resolution population exposure to PM_2.5 pollution based on multi-satellite retrievals: a case study of seasonal variation in the yangtze river delta, China in 2013[J]. Remote Sensing, 2019, 11(23). DOI:10.3390/rs11232724
[42]	Yin H, Pizzol M, Jacobsen J B, et al. Contingent valuation of health and mood impacts of PM_2.5 in Beijing, China[J]. Science of the Total Environment, 2018, 630: 1269-1282. DOI:10.1016/j.scitotenv.2018.02.275
[43]	Feng J L, Yu H, Liu S H, et al. PM_2.5 levels, chemical composition and health risk assessment in Xinxiang, a seriously air-polluted city in North China[J]. Environmental Geochemistry and Health, 2017, 39(5): 1071-1083. DOI:10.1007/s10653-016-9874-5
[44]	GBD 2019 Risk Factors Collaborators. Global burden of 87 risk factors in 204 countries and territories, 1990-2019:a systematic analysis for the Global Burden of Disease Study 2019[J]. The Lancet, 2020, 396(10258): 1223-1249.


环境科学 2023, Vol. 44 Issue (10): 5370-5381	PDF