2. 河北省环境演变与生态建设实验室, 石家庄 050024;
3. 河北省环境变化遥感识别技术创新中心, 石家庄 050024
2. Hebei Laboratory of Environmental Evolution and Ecological Construction, Shijiazhuang 050024, China;
3. Hebei Technology Innovation Center for Remote Sensing Identification of Environmental Change, Shijiazhuang 050024, China
流行病学研究表明短期或长期暴露于高浓度的PM2.5环境中会导致呼吸道、心血管和癌症的发病率和死亡率增加[1~3], 高分辨率PM2.5浓度时空变化的精准预测能够直接为上述污染健康影响评价提供基础支撑[4~7]; 同时, 亦能够为高精度追溯污染源及其排放强度的时空分布提供科学支撑[8].因此, PM2.5浓度时空变化的精准预测研究长期以来始终是大气污染基础研究领域的热点.
卫星遥感反演的气溶胶光学厚度(aerosol optical depth, AOD)与近地面PM2.5质量浓度之间存在紧密但复杂的相关关系, 使得AOD成为PM2.5浓度非常重要的代用指标, 目前已被广泛应用于近地面PM2.5浓度预测.AOD广泛的空间覆盖范围和对地球表面及大气的重复观测, 可以很好地填补由于地面监测网络站点稀疏而留下的数据空白[9~11].许多学者开发了多种统计模型建立PM2.5-AOD的相关关系, 早期统计模型(例如土地利用回归模型)既没有考虑到影响两者相关关系的预测因子(如相对湿度和大气边界层高度)具有时间变化特性, 也没有考虑到两者关系在空间上的非恒定性[12, 13].在高级统计模型方面, 2011年Lee等[14]在假设PM2.5-AOD间影响因子空间差异性很小的前提下, 构建了考虑时间随机效应的混合效应(linear mixed effect, LME)模型, 获得了较高精度的预测结果.鉴于在大区域范围内AOD等影响因子存在着空间差异性, Kloog等[15]提出了加入空间随机效应来校正空间差异性的时空混合效应模型, Hu等[16, 17]提出了在混合效应模型的基础上加入地理加权回归(geographical weighted regression, GWR)模型来校正空间差异性的两阶段统计模型, 进一步推进了统计模型的预测精度和稳健性.近年来, 人工智能模型也被广泛应用于近地面PM2.5浓度预测中, 该类模型可以较好地解释PM2.5-AOD之间的非线性关系, 较为流行的随机森林[18]、深度学习[19]和反向人工神经网络[20]等模型在模拟PM2.5-AOD的时空变化上表现出较优异的性能, 但模型对PM2.5本身的物理和地理特性顾及不足[21].
混合效应模型中除AOD这一主预测变量外, 还包括了辅助预测变量, 主要分为时间预测变量群和空间预测变量群两类, 前者包括气温、降水、风速、风向、相对湿度、气象能见度、气压和边界层高度等, 后者包括建设用地密度、道路密度、植被覆盖度、人口密度、耕地密度、污染源排放强度和海拔高度等, 此外, 还出现了一些交互项和AOD的二次项等预测变量.在不同区域模型中上述预测变量组合存在较明显差异[14~21], 其中, AOD的二次项等被认为在PM2.5污染较严重的区域能够纠正PM2.5浓度预测偏差[22, 23].
AOD产品的空间分辨率和覆盖度也是影响模拟精度的重要因素.以往用于预测PM2.5浓度的AOD产品大多来自于中分辨率成像光谱辐射计(MODIS)、多角度成像光谱辐射计(MISR)等传感器.其中以MODIS 10 km分辨率和MISR 17.6 km分辨率的AOD产品因其质量保障、持续时间长而被频繁使用[24~26].然而流行病学研究中对较小区域PM2.5浓度的暴露评估和中小尺度污染源识别, 许多地理单位的空间分辨率远远小于MODIS和MISR的空间分辨率[17]. 2018年, Lyapustin等[27]开发了一种新的多角度大气校正算法(multi-angle implementation of atmospheric correction, MAIAC), 并被用于计算1 km空间分辨率的AOD.北美和南亚等多地实验研究证实了MAIAC AOD与PM2.5浓度水平高度相关[28~32].Choi等[26]对多种气溶胶产品在东亚陆地上的表现进行比较, 发现MAIAC AOD与AERONET AOD的相关系数R达到0.93, 预期误差为0.68, 在所有遥感反演气溶胶产品中表现最好.许多研究也证明MAIAC AOD在中国表现性能良好[25, 33~35], 如MAIAC产品的精度和时空完整性均优于MODIS DT和DB产品[36, 37].
目前, 在中国区域使用MAIAC AOD产品进行PM2.5浓度预测的研究还相对较少, 其中, 使用MAIAC AOD产品结合两阶段统计模型预测PM2.5浓度的研究还没有报道.因此本文基于融合后的MAIAC AOD数据及气象和土地利用数据, 发展了一个两阶段统计模型, 在1 km的空间分辨率下预测京津冀地区2017年逐日PM2.5浓度的时空分布, 以期为该区域大气污染防治提供科学依据.
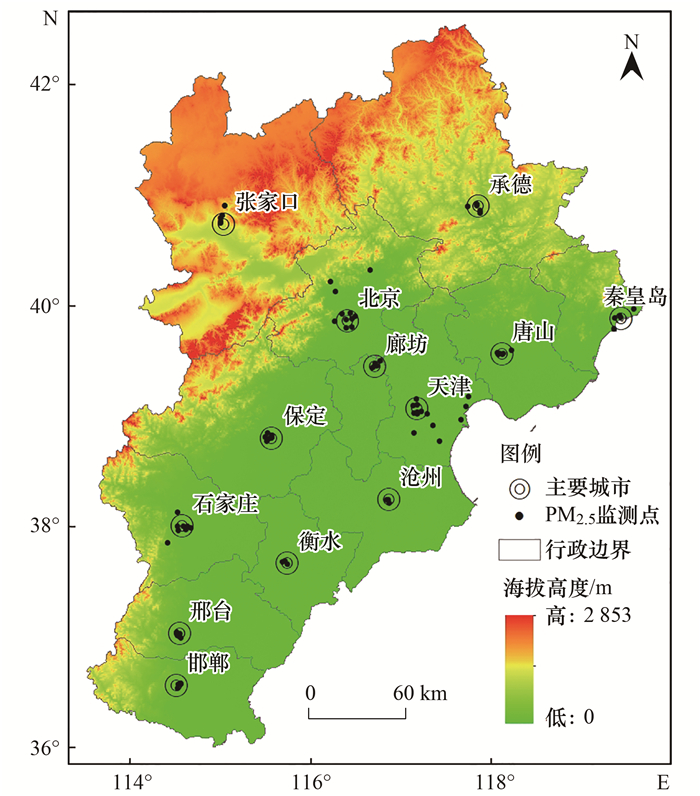
1 材料与方法 1.1 研究区概况京津冀地区位于中国北部, 包括北京和天津这2个直辖市以及河北省的11个地级市(图 1). 40年来, 该区域工业化和城市化发展迅速, 污染物排放强度较大[18].此外, 京津冀地区冬季的盛行风大多来自偏西或偏北方向, 而燕山山脉和太行山脉对盛行风起到了阻挡和削弱作用, 大气污染物质不易扩散, 使其成为中国大气污染特别是冬季污染最为严重的地区之一[38].
|
图 1 研究区地理位置及空气质量监测站点分布 Fig. 1 Location of the study area and spatial distribution of the PM2.5 monitoring stations |
2017年日平均PM2.5浓度数据来源于全国城市空气质量实时发布平台(http://106.37.208.233:20035/).本文采用了研究区79个国控监测站点数据(图 1), 处理过程中将不在监测值范围内(即 < 2 μg ·m-3和>500 μg ·m-3)的PM2.5浓度数据剔除.由于地理加权模型是根据点之间的距离来预测PM2.5浓度, 为了不改变PM2.5与各预测因子之间的关系, 少数距离接近的监测点予以保留[24].
1.2.2 MAIAC AODMAIAC AOD产品来源于NASA气候模拟中心(https://portal.nccs.nasa.gov/datashare/maiac/DataRelease/).本文采用了包括h03v01、h03v02和h04v01这3个条带数据内的2017年京津冀地区AOD数据.为提高空间覆盖率, 本文采用Terra和Aqua卫星融合后的MAIAC AOD数据.首先, 采用最小二乘法对Terra、Aqua逐月数据构建线性回归模型, 继而以此预测缺失的AOD值, 再将Terra和Aqua两星AOD值进行平均融合, 该平均值能更好地代表卫星过境时间10:30和13:30 AOD的平均状况[17].
1.2.3 气象数据采用的2017年气象数据包括行星边界层高度(planetary boundary layer height, PBLH)、风速、气温、相对湿度、地面气压和降水量等因子.其中, PBLH原始数据来源于第5版的戈达德地球观测系统数据同化系统的网格化气象数据产品(ftp://rain.ucis.dal.ca/ctm/), 水平空间分辨率为0.25°×0.312 5°的小时数据; 风速、气温、空气比湿、地面气压和降水量等原始气象数据来源于国家青藏高原数据中心(http://data.tpdc.ac.cn/zh-hans/data/)[39, 40], 水平空间分辨率为0.1°×0.1°的日平均值.为了进行数据集成, PBLH数据选取卫星过境两个时间段数据的平均值代表其日均情况, 所有气象数据采用双线性内插法重采样成与MAIAC AOD相同分辨率的栅格数据.
1.2.4 土地利用数据土地利用数据来源于地理国情监测云平台(http://www.dsac.cn/DataProduct/), 采用空间分辨率为30 m×30 m的2015年京津冀土地利用现状图来代表2017年的土地利用状况, 提取了森林覆盖率和建筑用地比率两个参数作为土地利用因子加入混合效应模型中, 在ArcGIS 10.3中主要利用区域统计工具来处理.
1.3 研究方法 1.3.1 模型构建本文采用一种两阶段统计模型对PM2.5-AOD关系的时空变化进行模拟.第一阶段模型是表征PM2.5与MAIAC AOD及气象因子、土地利用因子之间关系的混合效应模型.模型中除了固定效应外, 关键是加入了时间随机效应, 通过随机效应来体现组内数据的相关性和不同组数据的异质性[41], 实现对PM2.5-AOD关系在时间维的局部校正.在预测变量选择上, 除选择常规的时间与空间变量外, 针对研究区污染较严重的特点, 增加了AOD2和PBLH与AOD的交互项作为待选变量.经过变量选择和多重共线性诊断最终确定模型如下:
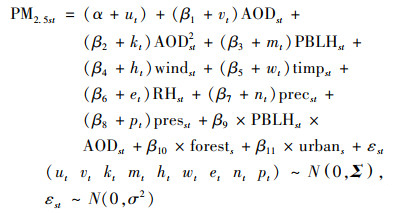
|
(1) |
式中, PM2.5st表示第s个地面监测点第t日的PM2.5浓度监测值; AODst表示相应的第s个地面监测点所在网格在第t日的气溶胶光学厚度值; AODst2表示第s个地面监测点所在网格在第t日的气溶胶光学厚度的平方值; PBLHst、windst、tempst、RHst、precst和presst分别表示第s个地面监测点所在网格在第t日相应的行星边界层高度、近地面风速、近地面气温、近地面相对湿度、降水量和近地面气压; PBLHst×AODst表示第s个地面监测点所在网格在第t日的边界层高度和气溶胶光学厚度的乘积; forests和urbans表示第s个地面监测点所在网格森林覆盖率和建设用地比率; α和ut分别为模型的固定截距和随机截距; β1~β11分别表示各自变量参数的固定效应斜率; vt、kt、mt、ht、wt、et、nt和pt为AOD和各气象变量的随机效应斜率; εts为模型第s个地面监测点在第t日的随机误差, 服从独立等方差多元正态分布; 各随机效应亦服从多元正态分布, 其中, Σ为随机效应的无结构方差-协方差矩阵.
在较大空间区域内, PM2.5-AOD的关系存在空间异质性, 为此, 在混合效应模型基础上, 引入第二阶段模型即地理加权模型, 实现对PM2.5-AOD关系空间异质性的校正[17, 42], 具体做法是在混合效应模型中嵌套地理加权模型, 也就是将混合效应模型预测得到的PM2.5浓度每日残差值(预测值-监测值)与MAIAC AOD进行地理加权模型拟合.GWR模型的核心是空间权重矩阵, 它是通过选取不同的空间权函数来表达对数据间空间关系的不同认识.具体的权重计算使用的核带宽函数采用近似高斯曲线的bi-square函数.由于PM2.5监测站点空间分布不均, 本研究选择自适应带宽, 最优带宽具有最小AICc值[43, 44].
地理加权模型具体表达式如下:
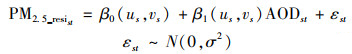
|
(2) |
式中, PM2.5_resist表示混合效应模型中地面监测站点s第t日的残差值, AODst表示站点s第t日的MAIAC AOD值, (us, vs)表示监测站点s的空间坐标, β0(us, vs)和β1(us, vs)分别表示监测站点处的回归截距和回归斜率, 随机误差项εst服从独立等方差正态分布.
最后, 混合效应模型预测结果叠加地理加权模型预测结果, 得到研究区近地面PM2.5浓度预测结果.
1.3.2 模型诊断与验证模型诊断是提高其稳健性的基本途径, 主要包括:对自变量多重共线性的诊断, 对模型假设条件的诊断包括对混合效应模型随机误差项正态分布和等方差的诊断、对两阶段模型随机误差项正态分布和等方差的诊断等.本文采用方差膨胀因子法(VIF)进行自变量多重共线性的诊断, 采用频率直方图法进行混合效应模型和两阶段模型随机误差项正态分布的诊断, 采用学生化残差的残差图法进行混合效应模型和两阶段模型的随机误差项等方差特性的诊断[45].
模型验证是评估模型预测精度的基本方法, 本文为了消除预测模型的过拟合问题, 采用十折交叉验证(ten-cross validation)方法获得站点PM2.5浓度预测值, 以站点观测值为自变量、预测值为因变量建立线性回归模型.采用该模型决定系数(R2)、模型斜率、均方根预测误差(RSMPE)和相对预测误差(RPE)等指标来评估模型的预测精度.其中, R2是预测值与观测值的拟合程度, R2越接近于1, 表明模型的预测精度越高; 斜率用来解释模型的预测偏差, 斜率越接近于1, 说明模型预测偏差越小; RSMPE反映模型预测的绝对误差, RPE反映模型预测的相对误差, 二者均为数值越小, 则模型预测精度越高.其中, RPE由于消除了均值大小带来的差异, 可以用于不同区域的比较.
RSMPE和RPE指标计算公式如下:
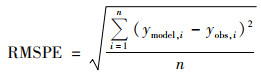
|
(3) |
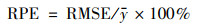
|
(4) |
式中, ymodel, i表示模型中站点PM2.5浓度预测值; yobs, i表示站点PM2.5浓度观测值; n为建模数据的样本总数; y为PM2.5浓度观测值的均值.
2 结果与分析 2.1 描述性统计2017年京津冀地区PM2.5地面监测站点有效观测数据为28 275个, 对应的AOD有效观测数据为17 288条, 根据建模要求, 每天匹配数据记录少于3对的数据被剔除, 最后得到覆盖323天的16 961条有效建模数据记录.
表 1为拟合模型的各变量描述性统计.其中, 2017年京津冀地区建模PM2.5浓度范围为3~499 μg ·m-3, 标准差为53.53 μg ·m-3, 表明研究区内污染程度时空差异较大.年均PM2.5浓度值为61.02 μg ·m-3, 远超过国家环境空气质量(GB 3095-2012)二级标准的限值(35 μg ·m-3)以及世界卫生组织空气质量准则IT-1的标准值[46], 说明京津冀地区PM2.5污染仍然较为严重.MAIAC AOD年均值为0.49, 标准差为0.52, AOD的时空差异同样较大.
|
|
表 1 2017年建模数据各参数的描述性统计 Table 1 Descriptive statistics of each parameter of the modeling data from 2017 |
2.2 模型拟合与诊断
首先采用逐步回归方法对模型进行变量选择, 然后对初步选取的独立自变量进行多重共线性检验, 当方差膨胀因子VIF>10且容忍度TV < 0.1时, 则存在多重共线性.结果表明(表 2), 参与模型的所有独立自变量均为VIF<10和TV>0.1, 表明独立自变量间不存在共线性问题.
|
|
表 2 多重共线性检验结果 Table 2 Multicollinearity test results |
模型拟合结果的随机误差项诊断表明(图 2), 第一阶段混合效应模型[图 2(a)]和两阶段模型[图 2(b)]的随机误差项频率直方图均符合正态分布的要求; 混合效应模型[图 2(c)]和两阶段模型[图 2(d)]的随机误差项学生化残差散点图在[-2, 2]区间的样本数比例分别达到了94.8%和95.8%, 并且散点基本呈现随机分布, 均符合等方差的要求.上述诊断结果保证了模型预测的稳健性.
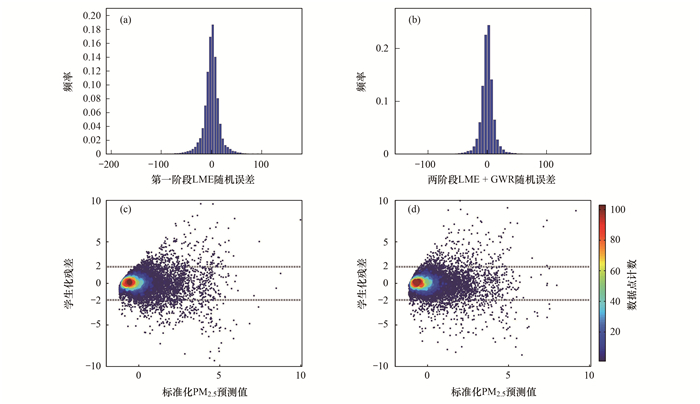
|
图 2 模型拟合结果的随机误差项诊断 Fig. 2 Random error term diagnosis of model fitting results |
表 3为混合效应模型自变量优选后固定效应的解.模型的固定效应(固定截距和固定斜率)表示全年内自变量对PM2.5浓度的固定影响, 其中, MAIAC AOD固定斜率为86.981, 说明PM2.5-AOD之间呈正相关; AOD2固定斜率为-21.087, 与PM2.5浓度呈负相关, 可能反映了PM2.5-AOD关系的跨季节对比; PBLH固定斜率为-0.036, 与PM2.5浓度呈现负相关性; PBLH×AOD的固定斜率为-0.039, 与PM2.5浓度呈负相关; 温度的固定斜率为2.102, 与PM2.5浓度呈正相关; 相对湿度固定斜率为38.745, 与PM2.5浓度呈明显的正相关; 地面气压的固定斜率为0.000 1, 说明地面气压越高越有利于PM2.5积累; 风速固定斜率为-0.798, 与PM2.5浓度呈负相关, 风速越大越有利于大气污染物的扩散; 降水量的固定斜率为-1.548, 与PM2.5浓度呈负相关, 说明降水对PM2.5有重要清除作用; 森林覆盖率的固定斜率为-12.972, 与PM2.5浓度呈负相关, 既反映了森林对PM2.5的清除作用也间接反映了人类活动影响微弱; 建设用地比率的固定斜率为-0.943, 可能与建模数据主要分布在城市建成区有关.
|
|
表 3 混合效应模型固定效应值 Table 3 Values of fixed effects in the first stage mixed effects model |
对全年中拥有有效数据的323 d每日运行地理加权模型并进行F分布逼近法检验, 结果表明(表 4), P值<0.05的次数比例达到99%, 模型参数估计的可靠性高.
|
|
表 4 地理加权模型F分布逼近法检验结果的P值分布 Table 4 The P-value distribution of results from the geographically weighted model, tested with the F distribution approximation method |
2.3 模型拟合结果的交叉验证
模型验证是评价模型预测精度的基本途径.图 3为混合效应模型和混合效应模型+地理加权模型拟合及交叉验证结果.结果表明, 单一LME模型拟合及交叉验证后的斜率分别为0.89和0.88, 决定系数R2分别为0.91和0.88, RMSPE和RPE分别为16.49 μg ·m-3和18.28 μg ·m-3, 表现出相当高的预测精度.GWR模型加入后, 模型拟合及交叉验证斜率分别提高到0.96和0.95, 表明LME+GWR模型的预测偏差较小, 能够更好克服“高值低估”问题; 并且拟合精度显著提升, 决定系数R2分别提升到0.96和0.94, 说明两阶段模型可以解释近地面PM2.5浓度94%以上的时空变化规律; 同时RMSPE和RPE也有明显降低, RMSPE分别减小到10.33 μg ·m-3和13.14 μg ·m-3, RPE分别减小到16.91%和21.42%.上述结果表明两阶段模型深刻揭示了PM2.5-AOD关系的时空异质性.
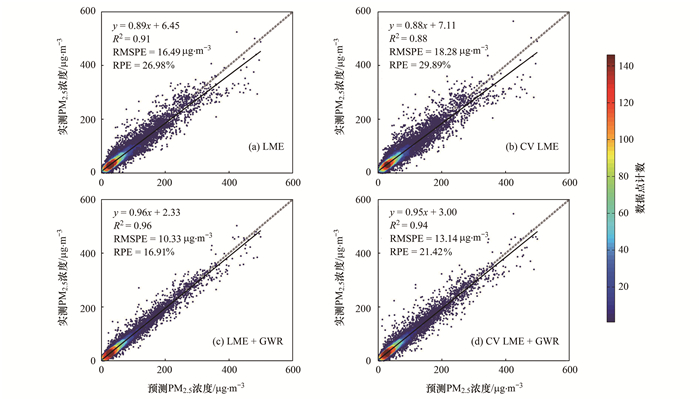
|
图 3 2017年LME模型和LME+GWR模型交叉验证结果对比 Fig. 3 Comparison of cross-validation results between LME model and LME+GWR model for 2017 |
图 4为基于两阶段模型交叉验证后, PM2.5监测站点在月、季和年尺度上观测值和预测值的拟合状况.与日值预测结果相比[图 3(d)], 随着时间尺度的增大, 模型的RMSPE和RPE逐渐减小, R2增大(年均值预测因为样本量偏少, 稍小于月均值和季均值预测); RMSPE分别为4.50、3.14和2.32 μg ·m-3; RPE分别为7.43%、5.25%和3.78%; R2分别为0.97、0.97和0.96.上述结果表明, 两阶段模型对月值以上尺度的预测精度又有显著提升.
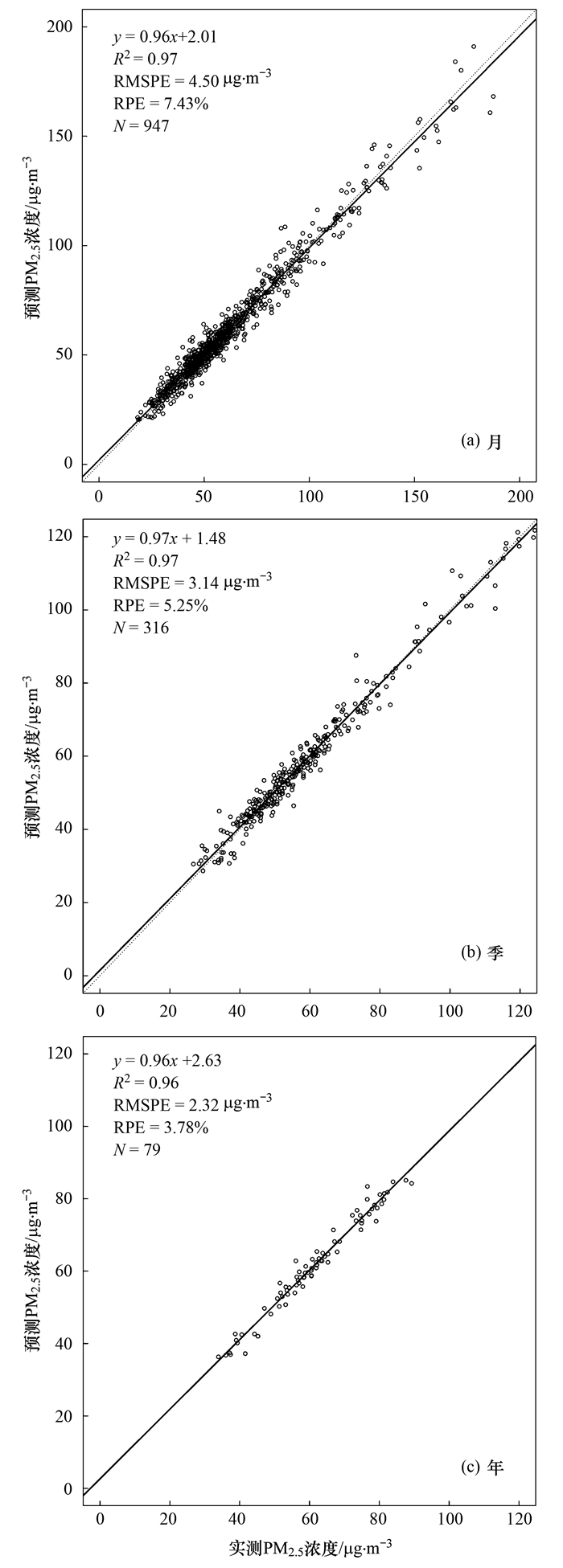
|
图 4 基于两阶段模型交叉验证结果的月、季和年时间尺度上站点的观测值和预测值拟合 Fig. 4 Comparison of predicted and observed PM2.5 concentrations, at monthly, seasonal, and yearly scales based on the results of cross-validation in the two-stage model |
基于两阶段模型预测出京津冀地区PM2.5浓度年均分布状况(图 5).从中可知, 2017年PM2.5浓度年均值范围在0~89.89 μg ·m-3之间, 全域年均值为44.96 μg ·m-3.PM2.5浓度低值区分布在北部燕山山区与坝上高原和西部太行山区, 这些区域人类活动较弱, 污染物排放强度小, 主要包括张家口、承德、北京西北部和秦皇岛北部等.平原东北部的PM2.5浓度为中值区, 推测原因是滨海部分主要得益于大气扩散条件好, 内陆部分以北京为代表主要得益于产业结构高端化带来的污染物排放强度相对较小.PM2.5浓度的高值区主要分布在平原西南部, 主要包括石家庄、保定、邢台和邯郸等, PM2.5年均值高于75 μg ·m-3.推测原因主要是人口众多、交通网和工业企业密集导致污染物排放强度较大, 同时处在太行山麓半封闭地形中, 冬季大气扩散条件差.
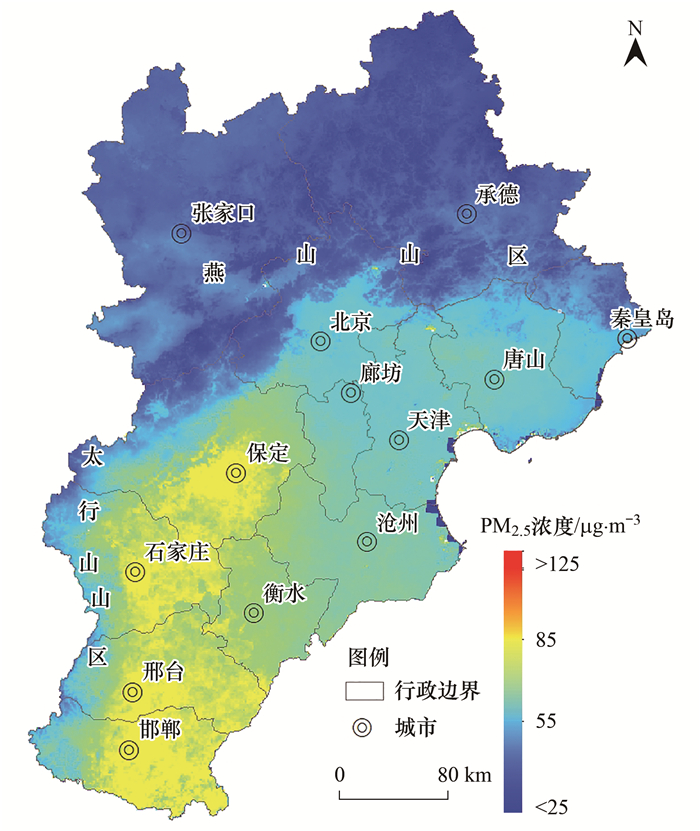
|
图 5 2017年PM2.5浓度年均值分布 Fig. 5 Annual mean distribution of PM2.5 concentration in 2017 |
全域PM2.5浓度具有较明显的季节差异(图 6).四季(3~5月为春季, 6~8月为夏季, 9~11月为秋季, 12、1和2月为冬季)PM2.5浓度季均值分别为42.80、36.92、42.07和55.97 μg ·m-3, 呈现“冬季高、夏季低和春秋过渡”的季节变化特点.冬季PM2.5浓度明显高于其他3个季节, 保定、石家庄、邢台和邯郸等市山麓平原地区在115 μg ·m-3以上, 同夏季相比, PM2.5提升30~60 μg ·m-3值不等, 推测原因主要是冬季民用采暖增大了污染物排放, 大气层结比较稳定, 较强的逆温极易出现[47, 48], 导致PM2.5等污染物快速积累.夏季PM2.5浓度低的主要原因是气温高、大气垂直扩散旺盛, 降水集中有利于污染物清除; 春季多风沙和扬尘天气, 是PM2.5的重要来源; 秋季大气层结向冬季转换, 扩散条件开始逐渐变差.
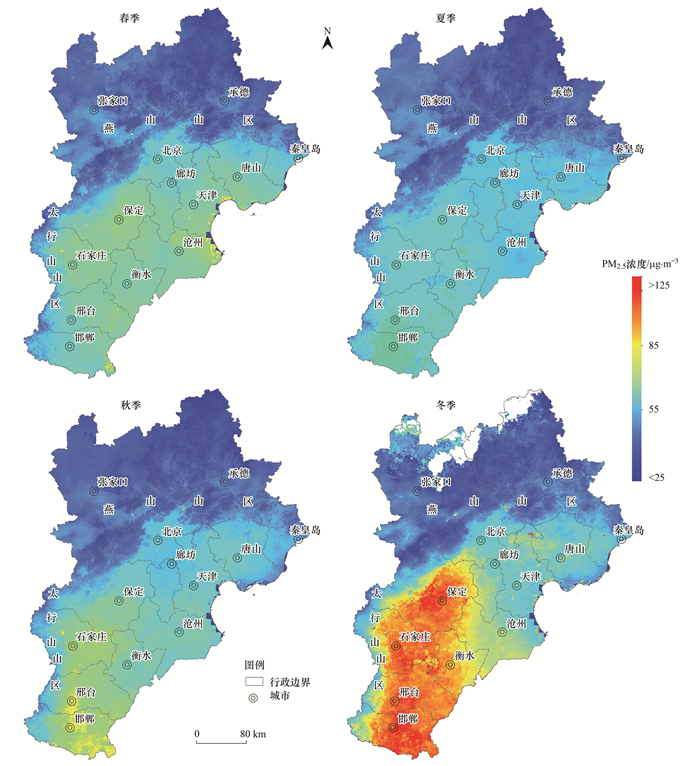
|
图 6 2017年各季节PM2.5平均浓度空间分布 Fig. 6 Spatial distribution of average PM2.5concentration in each season of 2017 |
当前研究区大气污染治理施策的最大不确定性在于精准识别污染源分布.在已知环境空气PM2.5浓度的时空分布条件下, 追踪污染物排放源的时空分布是一个复杂的物理化学过程.通过一定时间尺度聚合, 能够定性判断污染源的空间差异.一般来说, 大部分人为污染源的空间尺度会明显小于大气扩散条件均质空间的尺度.为此, 本文做如下假设:一次颗粒物和二次颗粒物的主要前体物的排放强度与PM2.5浓度呈正相关关系; 在月均值及其以上的时间尺度上, 较大空间尺度上的PM2.5浓度差异主要反映扩散条件的空间差异, 较小空间尺度上的PM2.5浓度差异主要反映污染物排放强度的空间差异.基于上述假设, 选择研究区污染最严重的冀中南山麓平原区, 分析不同空间尺度上PM2.5浓度的空间差异, 并初步推断污染源的空间分布特点.图 7为冀中南山麓平原冬季PM2.5浓度空间分布, 可以看出, 全域PM2.5浓度大体在105 μg ·m-3以上, 明显高于毗邻区域, 这一空间尺度的主要分异因素应归于大气扩散条件.区域内部的PM2.5浓度差异应归于污染源排放强度差异, 其中PM2.5污染较严重的地方(>105 μg ·m-3和 < 125 μg ·m-3)多分布在交通线两侧以及重点污染企业周围, 指示了传统重要污染源的空间分布; 而污染最严重的地方(>125 μg ·m-3, 图中蓝圈范围)与交通线和重点污染企业的分布不一致.笔者推测, 随着京津冀地区持续深入开展大气污染防治攻坚行动, 国家及省级重点监控企业的排放量减少, 导致重要污染源分布发生了变化.这种情况应当引起关注.
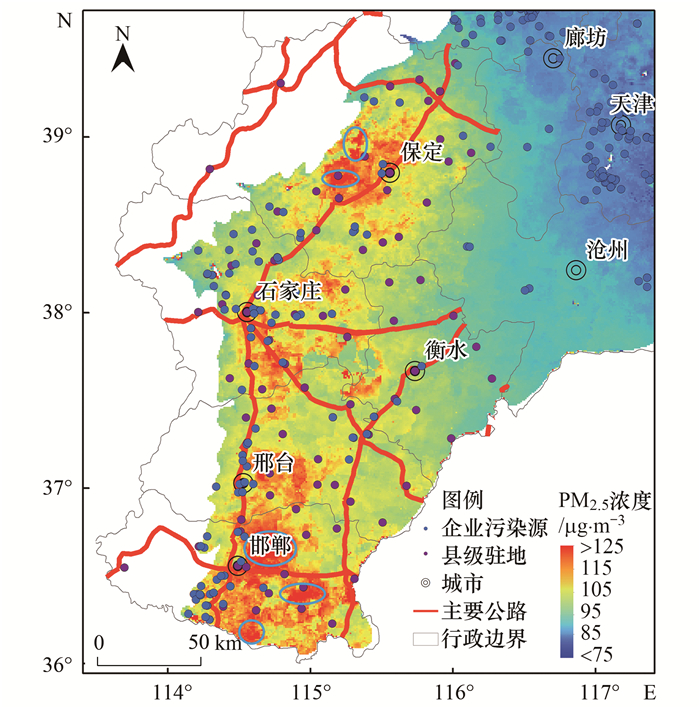
|
图 7 冀中南山麓平原冬季PM2.5浓度空间差异 Fig. 7 Spatial variation in PM2.5 concentration in winter over the piedmont plain of central and southern Hebei Province |
本文采用两阶段模型预测京津冀地区PM2.5浓度的时空分布, 其中第一阶段采用混合效应模型来反映PM2.5-AOD关系随时间变化规律, 第二阶段加入地理加权模型来反映PM2.5-AOD关系的空间变异.表 5为基于时空维模拟的相同或相似模型对比结果, 其中, 与同模型的研究[17]:2001~2010年美国东南部PM2.5浓度时空变化相比, R2有明显提高, 原因是在地理加权模型上该模型采用逐月拟合, 而本文采用逐日拟合, 使得模型预测精度提高; 与利用时空混合效应模型[28]预测2003~2011年美国东北部相比, R2提高; 与使用VIIRS AOD以及时间固定效应回归(TEFR)和GWR模型[49]相比, R2提高, RMSPE降低.表 6为与京津冀区域内使用各种主流方法的研究结果对比, 与同AOD分辨率使用DBN模型[6]和随机森林模型[18]相比, R2提高, 斜率提高, RMSPE有所降低, 模型精度明显提高.
|
|
表 5 与基于时空维模拟的相同或相近方法研究结果对比1) Table 5 Comparison of results from different studies with similar or identical methods and spatio-temporal dimensions |
|
|
表 6 与京津冀区域内使用各种主流方法的研究结果对比 Table 6 Comparison of results with those of other models commonly used in the Beijing-Tianjin-Hebei region |
3.2 AOD数据缺失对模型预测精度的影响
本文两阶段模型建模共获得2017年323 d的16 961对PM2.5-AOD有效数据, 全年平均时间有效数据比率为88%、空间有效数据比率为64.92%.表 7分别计算了每月AOD有效建模数据的时间和空间有效数据比率, 可以看出, 时空有效数据比率分别为70.9% ~100%和42.9% ~78.3%.有研究表明, AOD数据缺失较多会对模型预测精度产生影响, 京津冀地区AOD数据缺失往往与重污染天气相对应, 因此, 对模型预测精度的影响主要表现为“高值低估”, 并派生出“低值高估”问题, 产生预测偏差[25, 38].
|
|
表 7 2017年AOD时间和空间有效数据比率1)/% Table 7 Percentage of AOD data used for modeling in 2017/% |
为了探查AOD建模数据缺失对本文模型预测精度的影响, 图 8给出了基于站点的全部PM2.5浓度观测值的年均值与站点模型预测值的年均值拟合[图 8(a)]和基于站点建模PM2.5浓度观测值的年均值与站点模型预测值的年均值拟合[图 8(b)]的结果对比, 可以看出, AOD数据缺失产生了“高值低估”并派生出“低值高估”的预测偏差, 其中, 高值低估的最大值为9.2 μg ·m-3, 低值高估的最大值为8.0 μg ·m-3.可见AOD数据缺失对本模型预测精度影响不容忽视, 这是本研究下一步完善的方向之一.
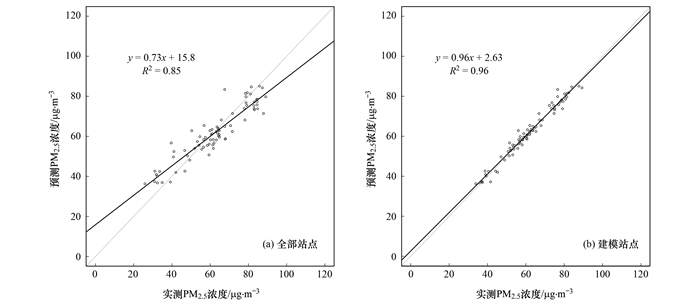
|
图 8 站点全部观测值和站点建模观测值的年均值与模型预测年均值拟合结果对比 Fig. 8 Measured and predicted annual mean regression results for all stations and modeled stations |
(1) PM2.5与AOD的直接线性相关性较低.本文构建了加入AOD2和PBLH与AOD乘积以及多变量的线性混合效应模型, 校正了PM2.5-AOD关系的时间差异性, 在此基础上加入了能够校正空间差异性的地理加权模型作为第二阶段模型.两阶段模型拟合结果与观测值验证的决定系数R2为0.96, 斜率为0.96, 十折交叉验证后R2为0.94, 斜率为0.95.说明上述两阶段模型通过对PM2.5-AOD关系在时空两个维度上进行局部校正, 可以极大提高两者之间的相关性, 模型模拟精度和改善偏差的能力均有明显提高.
(2) 与10 km MODIS AOD数据相比, 1 km空间分辨率的MAIAC AOD应用明显改善了PM2.5质量浓度站点数据与遥感AOD栅格数据由于空间尺度差异产生的拟合误差, 有效提高了模型的预测精度, 能够支持流行病学研究在城市尺度或更小区域的暴露评估, 也能对识别小尺度污染源的时空变化提供基础支持.
(3) 从两阶段模型预测的京津冀地区2017年PM2.5浓度时空分布状况可以看出, 在空间分布上, 污染严重的高值区分布在平原西南部, 中值区分布在平原东北部, 低值区分布在山区与高原; 在季节分布上, 表现为冬季高、夏季低和春秋过渡的特征.对污染最严重的冀中南山麓平原冬季PM2.5浓度空间分布深入分析可以发现, 污染最严重的小区域与主要交通线及重点污染企业等传统污染源的空间分布出现不一致, 可能出现了重要污染源的空间变化.
| [1] | Chow J C, Watson J G, Mauderly J L, et al. Health effects of fine particulate air pollution: lines that connect[J]. Journal of the Air & Waste Management Association, 2006, 56(10): 1368-1380. |
| [2] | Gao M, Saide P E, Xin J Y, et al. Estimates of health impacts and radiative forcing in winter haze in Eastern China through constraints of surface PM2.5 predictions[J]. Environmental Science & Technology, 2017, 51(4): 2178-2185. |
| [3] | Lyu D, Chen Z J, Almansoob S, et al. Transcriptomic profiling of human corneal epithelial cells exposed to airborne fine particulate matter (PM2.5)[J]. The Ocular Surface, 2020, 18(4): 554-564. DOI:10.1016/j.jtos.2020.06.003 |
| [4] | Lim S S, Vos T, Flaxman A D, et al. A comparative risk assessment of burden of disease and injury attributable to 67 risk factors and risk factor clusters in 21 regions, 1990-2010:a systematic analysis for the Global Burden of Disease Study 2010[J]. The Lancet, 2012, 380(9859): 2224-2260. DOI:10.1016/S0140-6736(12)61766-8 |
| [5] | Wang Q, Wang J N, He M Z, et al. A county-level estimate of PM2.5 related chronic mortality risk in China based on multi-model exposure data[J]. Environment International, 2018, 110: 105-112. DOI:10.1016/j.envint.2017.10.015 |
| [6] | 崔相辉. 京津冀地区PM2.5浓度预测模型建立与时空分析[D]. 泰安: 山东科技大学, 2018. |
| [7] | 马宗伟. 基于卫星遥感的我国PM2.5时空分布研究[D]. 南京: 南京大学, 2015. |
| [8] |
黄顺祥, 刘峰, 盛黎, 等. 基于伴随方法的大气污染溯源[J]. 科学通报, 2018, 63(16): 1594-1605. Huang S X, Liu F, Sheng L, et al. On adjoint method based atmospheric emission source tracing[J]. Chinese Science Bulletin, 2018, 63(16): 1594-1605. |
| [9] | Wang J, Christopher S A. Intercomparison between satellite-derived aerosol optical thickness and PM2.5 mass: implications for air quality studies[J]. Geophysical Research Letters, 2003, 30(21). DOI:10.1029/2003GL018174 |
| [10] | Gupta P, Christopher S A, Wang J, et al. Satellite remote sensing of particulate matter and air quality assessment over global cities[J]. Atmospheric Environment, 2006, 40(30): 5880-5892. DOI:10.1016/j.atmosenv.2006.03.016 |
| [11] | Hidy G M, Brook J R, Chow J C, et al. Remote sensing of particulate pollution from space: have we reached the promised land?[J]. Journal of the Air & Waste Management Association, 2009, 59(10): 1130-1139. |
| [12] | Gryparis A, Paciorek C J, Zeka A, et al. Measurement error caused by spatial misalignment in environmental epidemiology[J]. Biostatistics, 2009, 10(2): 258-274. DOI:10.1093/biostatistics/kxn033 |
| [13] |
余娟, 龚威, 朱忠敏. 高斯曲线优化能见度与气溶胶光学厚度转换模型[J]. 遥感学报, 2011, 15(5): 1008-1023. Yu J, Gong W, Zhu Z M. Optimized transformation model of aerosol optical depth and visibility based on Gaussian curve[J]. Journal of Remote Sensing, 2011, 15(5): 1008-1023. |
| [14] | Lee H J, Yiu Y, Coull B A, et al. A novel calibration approach of MODIS AOD data to predict PM2.5 concentrations[J]. Atmospheric Chemistry and Physics, 2011, 11(15): 7991-8002. DOI:10.5194/acp-11-7991-2011 |
| [15] | Kloog I, Sorek-Hamer M, Lyapustin A, et al. Estimating daily PM2.5 and PM10 across the complex geo-climate region of Israel using MAIAC satellite-based AOD data[J]. Atmospheric Environment, 2015, 122: 409-416. DOI:10.1016/j.atmosenv.2015.10.004 |
| [16] | Hu X, Waller L A, Lyapustin A, et al. 10-year spatial and temporal trends of PM2.5 concentrations in the Southeastern US estimated using high-resolution satellite data[J]. Atmospheric Chemistry and Physics, 2014, 14(12): 6301-6314. DOI:10.5194/acp-14-6301-2014 |
| [17] | Hu X F, Waller L A, Lyapustin A, et al. Estimating ground-level PM2.5 concentrations in the Southeastern United States using MAIAC AOD retrievals and a two-stage model[J]. Remote Sensing of Environment, 2014, 140: 220-232. DOI:10.1016/j.rse.2013.08.032 |
| [18] | Zhao C, Wang Q, Ban J, et al. Estimating the daily PM2.5 concentration in the Beijing-Tianjin-Hebei region using a random forest model with a 0.01°×-0.01° spatial resolution[J]. Environment International, 2020, 134. DOI:10.1016/j.envint.2019.105297 |
| [19] | Li L F, Franklin M, Girguis M, et al. Spatiotemporal imputation of MAIAC AOD using deep learning with downscaling[J]. Remote Sensing of Environment, 2020, 237. DOI:10.1016/j.rse.2019.111584 |
| [20] |
罗毅, 邓琼飞, 杨昆, 等. 近20年来中国典型区域PM2.5时空演变过程[J]. 环境科学, 2018, 39(7): 3003-3013. Luo Y, Deng Q F, Yang K, et al. Spatial-temporal change evolution of PM2.5 in typical regions of China in recent 20 years[J]. Environmental Science, 2018, 39(7): 3003-3013. |
| [21] |
沈焕锋, 李同文. 大气PM2.5遥感制图研究进展[J]. 测绘学报, 2019, 48(12): 1624-1635. Shen H F, Li T W. Progress of remote sensing mapping of atmospheric PM2.5[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(12): 1624-1635. |
| [22] | Xiao Q Y, Wang Y J, Chang H H, et al. Full-coverage high-resolution daily PM2.5 estimation using MAIAC AOD in the Yangtze River Delta of China[J]. Remote Sensing of Environment, 2017, 199: 437-446. DOI:10.1016/j.rse.2017.07.023 |
| [23] | Zheng Y X, Zhang Q, Liu Y, et al. Estimating ground-level PM2.5 concentrations over three megalopolises in China using satellite-derived aerosol optical depth measurements[J]. Atmospheric Environment, 2016, 124: 232-242. DOI:10.1016/j.atmosenv.2015.06.046 |
| [24] | Hu X F, Waller L A, Al-Hamdan M Z, et al. Estimating ground-level PM2.5 concentrations in the Southeastern U.S. using geographically weighted regression[J]. Environmental Research, 2013, 121: 1-10. DOI:10.1016/j.envres.2012.11.003 |
| [25] | Liang F C, Xiao Q Y, Wang Y J, et al. MAIAC-based long-term spatiotemporal trends of PM2.5 in Beijing, China[J]. Science of the Total Environment, 2018, 616-617: 1589-1598. DOI:10.1016/j.scitotenv.2017.10.155 |
| [26] | Choi M, Lim H, Kim J, et al. Validation, comparison, and integration of GOCI, AHI, MODIS, MISR, and VIIRS aerosol optical depth over East Asia during the 2016 KORUS-AQ campaign[J]. Atmospheric Measurement Techniques, 2019, 12(8): 4619-4641. DOI:10.5194/amt-12-4619-2019 |
| [27] | Lyapustin A, Wang Y J, Korkin S, et al. MODIS collection 6 MAIAC algorithm[J]. Atmospheric Measurement Techniques, 2018, 11(10): 5741-5765. DOI:10.5194/amt-11-5741-2018 |
| [28] | Kloog I, Chudnovsky A A, Just A C, et al. A new hybrid spatio-temporal model for estimating daily multi-year PM2.5 concentrations across Northeastern USA using high resolution aerosol optical depth data[J]. Atmospheric Environment, 2014, 95: 581-590. DOI:10.1016/j.atmosenv.2014.07.014 |
| [29] | Chudnovsky A A, Koutrakis P, Kloog I, et al. Fine particulate matter predictions using high resolution Aerosol Optical Depth (AOD) retrievals[J]. Atmospheric Environment, 2014, 89: 189-198. DOI:10.1016/j.atmosenv.2014.02.019 |
| [30] | Jethva H, Torres O, Yoshida Y. Accuracy assessment of MODIS land aerosol optical thickness algorithms using AERONET measurements over North America[J]. Atmospheric Measurement Techniques, 2019, 12(8): 4291-4307. DOI:10.5194/amt-12-4291-2019 |
| [31] | Martins V S, Lyapustin A, de Carvalho L A S, et al. Validation of high-resolution MAIAC aerosol product over South America[J]. Journal of Geophysical Research: Atmospheres, 2017, 122(14): 7537-7559. DOI:10.1002/2016JD026301 |
| [32] | Mhawish A, Banerjee T, Sorek-Hamer M, et al. Comparison and evaluation of MODIS multi-angle implementation of atmospheric correction (MAIAC) aerosol product over South Asia[J]. Remote Sensing of Environment, 2019, 224. DOI:10.1016/j.rse.2019.01.033 |
| [33] | Huang K Y, Xiao Q Y, Meng X, et al. Predicting monthly high-resolution PM2.5 concentrations with random forest model in the North China Plain[J]. Environmental Pollution, 2018, 242(Pt A): 675-683. |
| [34] | Li R K, Ma T X, Xu Q, et al. Using MAIAC AOD to verify the PM2.5 spatial patterns of a land use regression model[J]. Environmental Pollution, 2018, 243: 501-509. DOI:10.1016/j.envpol.2018.09.026 |
| [35] | Tao M H, Wang J, Li R, et al. Performance of MODIS high-resolution MAIAC aerosol algorithm in China: characterization and limitation[J]. Atmospheric Environment, 2019, 213: 159-169. DOI:10.1016/j.atmosenv.2019.06.004 |
| [36] | Liu N, Zou B, Feng H H, et al. Evaluation and comparison of multiangle implementation of the atmospheric correction algorithm, Dark Target, and Deep Blue aerosol products over China[J]. Atmospheric Chemistry and Physics, 2019, 19(12): 8243-8268. DOI:10.5194/acp-19-8243-2019 |
| [37] | Zhang Z Y, Wu W L, Fan M, et al. Evaluation of MAIAC aerosol retrievals over China[J]. Atmospheric Environment, 2019, 202: 8-16. DOI:10.1016/j.atmosenv.2019.01.013 |
| [38] |
郝静, 孙成, 郭兴宇, 等. 京津冀内陆平原区PM2.5浓度时空变化定量模拟[J]. 环境科学, 2018, 39(4): 1455-1465. Hao J, Sun C, Guo X Y, et al. Simulation of the spatio-temporally resolved PM2.5 aerosol mass concentration over the Inland Plain of the Beijing-Tianjin-Hebei Region[J]. Environmental Science, 2018, 39(4): 1455-1465. |
| [39] | He J, Yang K, Tang W J, et al. The first high-resolution meteorological forcing dataset for land process studies over China[J]. Scientific Data, 2020, 7(1). DOI:10.1038/s41597-020-0369-y |
| [40] | Yang K, He J, Tang W J, et al. On downward shortwave and longwave radiations over high altitude regions: observation and modeling in the Tibetan Plateau[J]. Agricultural and Forest Meteorology, 2009, 150(1): 38-46. |
| [41] |
王明高, 孟生旺. 贝叶斯非线性混合效应模型及其应用研究[J]. 统计与信息论坛, 2016, 31(12): 10-16. Wang M G, Meng S W. Bayesian nonlinear mixed effects models and their applications[J]. Statistics & Information Forum, 2016, 31(12): 10-16. DOI:10.3969/j.issn.1007-3116.2016.12.002 |
| [42] |
付宏臣, 孙艳玲, 王斌, 等. 基于AOD数据和GWR模型估算京津冀地区PM2.5浓度[J]. 中国环境科学, 2019, 39(11): 4530-4537. Fu H C, Sun Y L, Wang B, et al. Estimation of PM2.5 concentration in Beijing-Tianjin-Hebei region based on AOD data and GWR model[J]. China Environmental Science, 2019, 39(11): 4530-4537. DOI:10.3969/j.issn.1000-6923.2019.11.006 |
| [43] |
陈辉, 厉青, 张玉环, 等. 基于地理加权模型的我国冬季PM2.5遥感估算方法研究[J]. 环境科学学报, 2016, 36(6): 2142-2151. Chen H, Li Q, Zhang Y H, et al. Estimations of PM2.5 concentrations based on the method of geographically weighted regression[J]. Acta Scientiae Circumstantiae, 2016, 36(6): 2142-2151. |
| [44] | 郭玮. 基于两阶段模型的京津冀地区PM2.5浓度时空变化研究[D]. 石家庄: 河北师范大学, 2020. |
| [45] | 何晓群, 闵素芹. 实用回归分析[M]. ((第二版)). 北京: 高等教育出版社, 2014. |
| [46] | World Health Organization. Air quality guidelines global update 2005: particulate matter, ozone, nitrogen dioxide and sulfur dioxide[R]. Copenhagen, Denmark: WHO, 2006. |
| [47] |
王晨, 时悦, 景悦, 等. 基于遥感数据的京津冀地区PM2.5时空分布特征[J]. 环境监测管理与技术, 2020, 32(1): 37-41. Wang C, Shi Y, Jing Y, et al. Spatial and temporal distribution characteristics of PM2.5 in Beijing-Tianjin-Hebei Region based on remote sensing data[J]. The Administration and Technique of Environmental Monitoring, 2020, 32(1): 37-41. |
| [48] |
金囝囡, 杨兴川, 晏星, 等. 京津冀及周边MAIAC AOD和PM2.5质量浓度特征及相关性分析[J]. 环境科学, 2021, 42(6): 2604-2615. Jin J N, Yang X C, Yan X, et al. MAIAC AOD and PM2.5 mass concentration characteristics and correlation analysis in Beijing-Tianjin-Hebei and surrounding areas[J]. Environmental Science, 2021, 42(6): 2604-2615. |
| [49] | Yao F, Wu J S, Li W F, et al. A spatially structured adaptive two-stage model for retrieving ground-level PM2.5 concentrations from VIIRS AOD in China[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2019, 151: 263-276. DOI:10.1016/j.isprsjprs.2019.03.011 |
 2021, Vol. 42
2021, Vol. 42


