2. 中国气象局大气化学重点开放实验室, 北京 100089;
3. 京津冀环境气象预报预警中心, 北京 100089;
4. 北京大学环境科学与工程学院, 北京 100871
2. Key Laboratory of Atmospheric Chemistry, China Meteorological Administration, Beijing 100089, China;
3. Environmental Meteorology Forecast Center of Beijing-Tianjin-Hebei, China Meteorological Administration, Beijing 100089, China;
4. College of Environmental Science and Engineering, Peking University, Beijing 100871, China
臭氧(ozone, O3)是地球大气中重要的痕量气体, 对大气化学循环、农作物和人类健康及生活有着重要影响[1~4].对流层臭氧是大气环境中重要的二次污染物, 其作为一种强氧化剂, 是大气中·OH的主要来源[5, 6], 可通过氧化作用影响大气中一些痕量气体的大气寿命, 对对流层的光化学循环起着至关重要的作用[7]; 作为第三大温室气体, 估算其全球辐射强迫约为(0.40±0.20)W·m-2, 对全球气候有重要影响; 地表臭氧还会影响人体健康和农作物的生长[8~10].
中国超大城市及周边地区日益严重的地表和边界层臭氧污染受到研究者的广泛关注[11~19].在京津冀、长三角和珠三角等主要城市区域, 已观测到臭氧浓度超过环境空气质量标准的100%~200%, 而京津冀地区又是上述几个地区中臭氧污染最严重的区域[4, 14~19]. 2005年夏季Wang等[18]在北京西北郊区的山区站点进行了6周的外场观测, 观测到地表臭氧的小时体积分数最高值高达286×10-9. Ma等[19]利用上甸子本底站的地表臭氧观测数据研究表明, 北京地区地表臭氧浓度自2003年以来呈现逐年上升的趋势.面对京津冀地区日益严重的臭氧超标污染情况, 十分有必要提高对臭氧浓度的观测监控能力及公众的预警防范能力, 开展相关大气臭氧浓度的预报工作, 以有效保护民众的身体健康.
目前国内外臭氧浓度预报采用的方法主要可分为统计预报方法和数值预报方法两大类[20~23].北京市气象局已有BREMPS空气质量模式对PM2.5以及臭氧进行业务化的预报服务, 但是该模型对于夏季臭氧高浓度存在明显的低估问题[23].相比于数值预报方法, 统计预报方法在模型建立时, 输入数据较少, 计算成本较低, 可推广性较强, 是本研究中拟采用的研究方法.时间序列分析方法包括频域分析方法和时域分析方法, 在统计预报中有着广泛的应用[24~27].时域分析方法最早可以追溯到1927年, 有研究者提出了自回归(autoregressive, AR)模型, 随后Walker在分析印度大气规律时使用了移动平均(moving average, MA)模型和自回归移动(autoregressive moving average, ARMA)模型[25].Box等[27]在总结前人研究的基础上提出了差分自回归移动平均(autoregressive integrated moving average, ARIMA)模型, 其研究极大推动了时间序列分析研究的发展, 在社会和自然科学的多个领域有着广泛应用.ARIMA时间序列分析模型可以利用差分方法简单高效提取非平稳时间序列中的确定性信息, 因此在非平稳时间序列的研究和预测中有重要的应用价值.近地表臭氧作为一种大气二次污染物, 决定其浓度的物理和化学过程相对复杂, 其浓度时间序列为非平稳时间序列, 因此ARIMA时间序列模型应用于臭氧中长期预报具有理论可行性和实际可操作性.
1 材料与方法 1.1 观测数据用于臭氧长期预报和动态ARIMA模型构建及有效预报时长分析的臭氧浓度观测数据来自华北区域大气本底站——上甸子观测站(40°39′N, 117°07′E), 臭氧观测使用的仪器是美国Thermo公司生产的TE49C型臭氧分析仪.仪器在使用之前和每月定期利用TE49CPS臭氧校准仪校准, 并在日常观测中每天进行零点和跨度检查, 保证观测结果的准确性.该站点位于北京城区东北方向的密云区高岭镇上甸子村, 距离北京市中心约100 km.站点远离市中心和人口密集区域, 受局地人为排放源的影响极小.该站点是世界气象组织全球大气观测(WMO/GAW)在我国设立的区域大气本底站之一, 也是我国首批入选的大气成分本底野外观测站之一, 其臭氧观测数据具有区域代表性.
用于动态ARIMA模型中长期预报普适性分析的2015~2019年臭氧日最大8h滑动平均数据来自于中国环境监测总站, 数据经过完整性和有效性审核.用于动态ARIMA模型建模的2015~2019年上甸子、天津和保定站点的日最高气温资料来自于国家气象信息中心及中国气象数据网(http://data.cma.cn/).臭氧日最大8h滑动平均值根据《中华人民共和国国家环境保护标准》(HJ 663-2013)计算, 观测数据的样本量信息如表 1所示, 上甸子站、天津站和保定站的有效数据百分比分别为98%、94%和89%, 数据完整性较好, 可以满足时间序列分析建模的要求.
|
|
表 1 臭氧日最大8 h滑动平均值数据样本量统计 Table 1 Sample size of ozone maximum 8 h average value |
1.2 ARIMA方法简介
ARIMA模型, 即差分自回归移动平均模型, 是时间序列时域分析的方法之一[25, 26].时间序列时域分析方法从序列自相关的角度揭示时间序列的发展规律, 主要包括AR模型, MA模型, ARIMA模型, 自回归条件异方差模型(autoregressive conditional heteroskedasticity model, ARCH)及其衍生模型等.ARIMA模型是在AR模型和MA模型基础上发展出的方法, 该模型可通过差分法将非平稳时间序列平稳化, 可克服AR模型和MA模型只能处理平稳时间序列的缺点.同时该模型相对于ARCH模型及其衍生模型具有结构简单, 输入变量少的特点, 是单变量时间序列数据预测的最广泛使用方法之一, 方便业务化推广.ARIMA模型记为ARIMA(p, d, q), 其中p为AR模型阶数, q为MA模型阶数, d为差分阶数.模型的一般表达式如下:
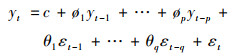
|
式中, yt为差分序列, εt为噪声序列, ø为AR模型拟合参数, θ为MA模型拟合参数.
季节性ARIMA模型(seasonal ARIMA model)是在ARIMA模型中引入季节性的项, 记为ARIMA(p, d, q) (P, D, Q)s, 其中, p、d和q表示模型中非季节部分的模型参数, P、D和Q表示模型中季节性部分的模型参数, s为季节性周期.
一般来说, 建立ARIMA模型有3个阶段, 分别是模型识别和定阶、参数估计和模型检验[25].模型识别和定阶主要是根据自相关图(ACF图)和偏自相关图(PACF图)截尾和拖尾性质来确定模型参数p、q和d.参数估计主要是根据赤池信息准则(AIC准则)和贝叶斯信息准则(BIC准则)选择最优预测模型.模型检验主要包括参数估计的显著性检验和残差是否为随机独立的白噪声序列.
预报中, 如果考虑外部变量(如气温等)的变动对预测变量的影响, 可以将外部变量作为协变量纳入ARIMA模型, 对ARIMA模型进行扩展.本研究中将未加入协变量的ARIMA模型定义为一般ARIMA模型, 将加入日最高气温及二次项作为协变量的ARIMA模型定义为动态ARIMA模型.本研究采用2007~2019年上甸子臭氧浓度月均值数据和2015~2019年上甸子站点、天津和保定站点的臭氧日最大8 h滑动平均值数据进行AIRMA时间序列建模分析, 构建臭氧预报的时间序列分析模型, 对预报的结果进行参数评估, 验证ARIMA时间序列分析方法在京津冀地区臭氧中长期预报中的适用性.本文中臭氧预报的时间序列分析利用R语言的forecast包完成.
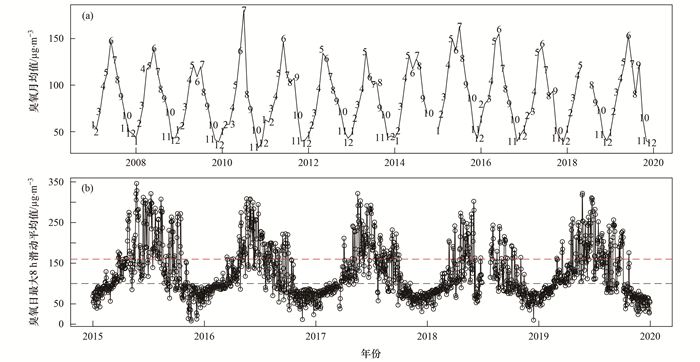
2 结果与讨论 2.1 上甸子站点臭氧时间序列变化特征图 1为上甸子臭氧的月均值和日最大8h滑动平均值, 结果表明, 上甸子所在京津冀地区臭氧浓度变化呈现明显的季节性, 5~8月臭氧浓度较高, 易发臭氧污染.2015~2019年, 上甸子站点臭氧日最大8 h滑动平均值超过《环境空气质量标准》(GB 3095-2012)二级标准限值的天数平均为97 d, 平均超标率为26.7%(表 2).上甸子站点夏季臭氧超标率近年来维持在较高水平, 表明京津冀地区面临的臭氧污染问题的严重性.因此, 十分有必要开展相关研究, 发展臭氧客观预报方法, 提升臭氧污染中长期预报的准确性, 开展精细化臭氧预报预警业务, 保护民众身体健康.
|
(a)线上数值表示月份; (b)蓝色虚线:《环境空气质量标准》(GB 3095-2012)臭氧一级标准限值; (b)红色虚线:《环境空气质量标准》(GB 3095-2012)臭氧二级标准限值 图 1 上甸子站点臭氧浓度时间序列 Fig. 1 Time series of ozone at the SDZ site |
|
|
表 2 上甸子臭氧超标情况统计 Table 2 Statistics of ozone pollution at the SDZ site |
2.2 利用季节性ARIMA模型进行臭氧月均值预报
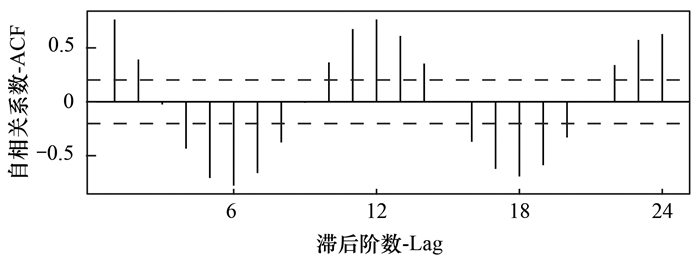
考虑低时间分辨率的污染物长期数据的易获取性和消除日变化和周变化波动对长期预报的影响, 本研究采用上甸子臭氧浓度月均值开展臭氧长期预报.上甸子臭氧浓度月均值的时间序列(图 1)和ACF图(图 2)表明, 该站点2007~2019年臭氧浓度月均值具有明显的季节性, 该时间序列为非平稳时间序列, 在ARIMA建模预测时要首先对其进行平稳化处理, 将时间序列转变为平稳时间序列.对数变换和差分是实现时间序列平稳化常用的方法, 对季节性时间序列, 应根据季节周期进行季节化差分.
|
蓝色虚线: 自相关系数2倍标准差 图 2 上甸子站点臭氧月均值ACF图 Fig. 2 ACF chart of monthly average ozone at the SDZ site |
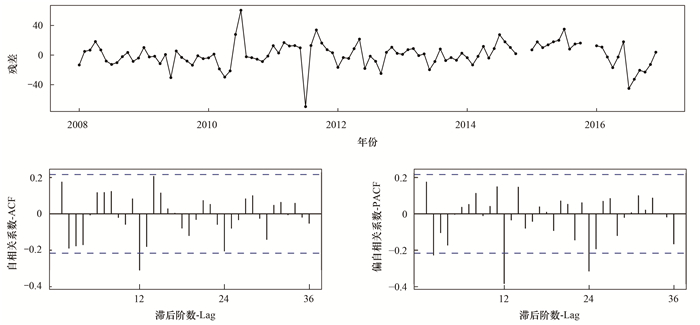
结合差分平稳化处理后的ACF和PACF图(图 3), 可以构建臭氧月均值预报的ARIMA模型.其中, 差分平稳化后的ACF图显示在滞后12阶有明显的突起, 该突起显示出季节性MA(1) 的成分.在PACF图中, 在滞后2阶时(PACF图中左起第2根竖垂线)的突起显示出数据包含非季节性AR(1) 的成分, 而滞后12和24阶的突起则显示出季节性AR(2) 的成分.因此综合考虑, 构建一个可能的ARIMA模型为ARIMA(0, 0, 2)(2, 1, 1)12.用该模型以及该模型的衍生模型进行拟合, 并计算了衍生模型的AICc、AIC和BIC值.在同阶差分模型中, ARIMA(0, 0, 1)(1, 1, 1)12模型中的AICc值最小, 因此可以选择ARIMA(0, 0, 1)(1, 1, 1)12模型为最优模型.
|
蓝色虚线: 自相关系数和偏自相关系数2倍标准差 图 3 上甸子臭氧月均值时间序列1阶季节性差分变换平稳化处理后残差、 Fig. 3 Time series of residuals, ACF, and PACF plots after the first-order seasonal difference transformation of the monthly average ozone value at the SDZ site |
同时本研究使用2007~2016年上甸子臭氧月均值数据作为训练集进行模型拟合, 将2017~2019年上甸子臭氧月均值数据作为测试集进行预测, 评估模型的预测效果(表 3).对不同模型测试集的评估发现ARIMA(0, 0, 1)(1, 1, 1)12模型拥有最小的均方根误差(RMSE), 表明该模型在对臭氧月均值的预报中具有良好的预报性能(表 3).同时为了验证模型的适用性, 本研究将季节性ARIMA模型与指数平滑模型(ETS模型)进行了比较, 结果发现季节性ARIMA模型比ETS模型在臭氧月均值预报中具有更小的均方根误差, 说明季节性ARIMA模型预报结果优于ETS模型.ETS模型是季节性数据预报中常用的时间序列分析预报模型, 在污染物预报中具有广泛的应用.本研究中臭氧月均值预报采用的季节性ARIMA模型与ETS模型相比准确度更高, 进一步说明季节性ARIMA模型在臭氧的月均值长期预报中具有很好的适用性.
|
|
表 3 臭氧月均值ARIMA模型参数评价 Table 3 Evaluation of ARIMA model parameters for predicting monthly average ozone values |
图 4给出了上甸子2017~2019年臭氧月均值季节性ARIMA模型预测值和观测值的对比, 可以看出预测值和观测值变化趋势吻合较好, 计算模型预测值和观测值的相关系数R可达0.951, 该模型可以用于臭氧长期变化趋势的预测和评估.
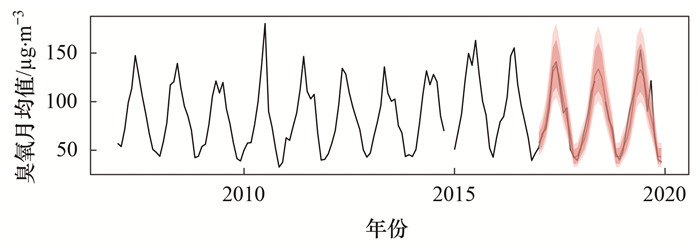
|
红色阴影区域: 预测值和置信区间 图 4 上甸子站点臭氧月均值预报结果 Fig. 4 Prediction of monthly average ozone values at the SDZ site |
在上述对于臭氧月均值的预报中, 仅利用长期臭氧月均值的历史观测资料进行季节性ARIMA模型建模, 就能实现对未来3 a臭氧月均值的准确预报.由于污染物长期变化趋势波动相对较小, 因此在预报建模时没有考虑随时间推移外部气象因素的影响.而在对高时间分辨率的臭氧浓度(如臭氧日最大8 h滑动平均值)的预测中, 考虑外部气象因子的影响, 可以提高时间序列分析模型的预报准确度.已有研究发现, 臭氧的日最大8 h滑动平均值和日最高气温存在很好的相关性[28~30].因此在臭氧日最大8 h的预报中, 考虑将日最高气温及其二次项作为协变量加入ARIMA模型中, 建立动态ARIMA模型, 进行臭氧日最大8 h滑动平均值的预测.
在模型中加入日最高气温及其二次项作为协变量, 利用auto.arima()函数根据AICc选择合适的拟合模型进行臭氧日最大8 h滑动平均值预测建模.在进行预测前, 需对构建的模型进行ARIMA残差的白噪声检验.图 5结果表明, 构建模型的残差值在y=0上下小幅波动, 其期望为0, 方差固定.残差序列表现为自相关特征, 在任何Lag时差的序列之间自相关系数值在2倍标准差范围内, 近似为0(图 5).残差序列为正态分布, 且Ljung-Box Q统计量检验的P值为0.19(大于0.05), 进一步证明该模型拟合的残差时间序列为白噪声.综上, 经过统计检验表明可以利用上述动态ARIMA模型, 进行臭氧日最大8 h滑动平均值的预报.
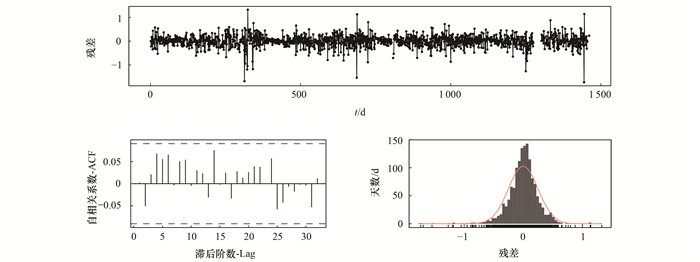
|
蓝色虚线: 自相关系数2倍标准差 图 5 动态ARIMA模型拟合残差检验 Fig. 5 Residual test of dynamic ARIMA model |
利用2015~2018年的臭氧日最大8 h滑动平均值数据作为训练集, 分别进行一般ARIMA模型和动态ARIMA模型拟合, 结果表明两种时间序列分析模型均具有较好的拟合效果, 模型的拟合值和观测值变化趋势吻合较好, 且观测值和模拟值之间的偏差较小.相比较而言, 动态ARIMA模型的RMSE值(29.9 μg·m-3)较一般ARIMA模型的RMSE值(32.3 μg·m-3)更小, 相关系数R更高(图 6).动态ARIMA模型在加入日最高气温及二次项作为协变量以后具有更好的拟合效果.因此, 在对臭氧日最大8 h滑动平均值的预报中采用此方法对2019年4~10月的臭氧日最大8 h滑动平均值进行滚动预报, 评估模型的预报效果.
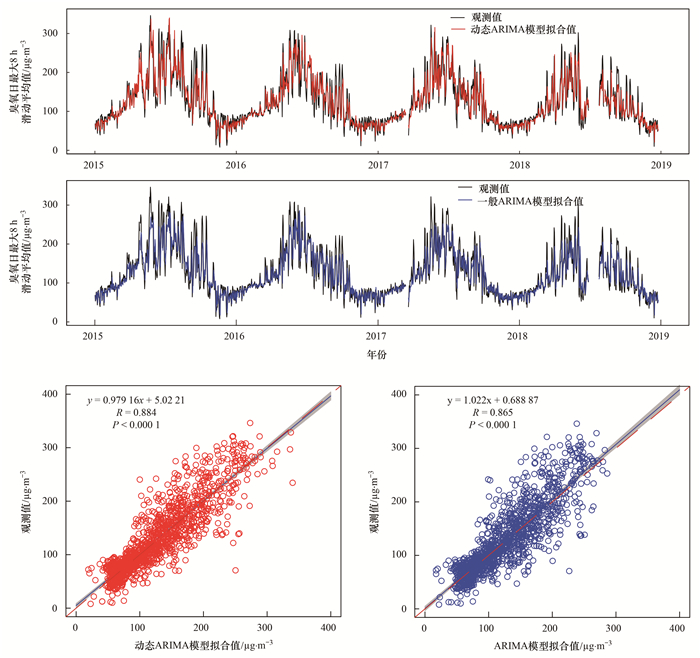
|
图 6 上甸子站一般ARIMA模型和动态ARIMA模型的拟合结果 Fig. 6 Fitting results of normal ARIMA model and dynamic ARIMA model at the SDZ site |
图 7给出了2019年4~10月上甸子臭氧日最大8 h滑动平均值动态ARIMA模型和一般ARIMA模型的7 d滚动预报的预测值和观测值的对比, 结果表明, 尽管动态ARIMA模型和一般ARIMA模型在训练集的拟合中均表现良好, 但是其模型的预报性能相差较大.加入了日最高气温及其二次项作为协变量的动态ARIMA模型, 模型预测值和观测值变化趋势一致性较好, 模型预测值和观测值的相关系数为0.670, RMSE为45.6 μg·m-3, 模型总体具有较好的预报准确性.但是未加入日最高气温及其二次项作为协变量的ARIMA模型, 模型预测值和观测值的相关系数仅为0.296, 预测值和观测值存在较大偏差, 不能满足臭氧中长期预报的需求.
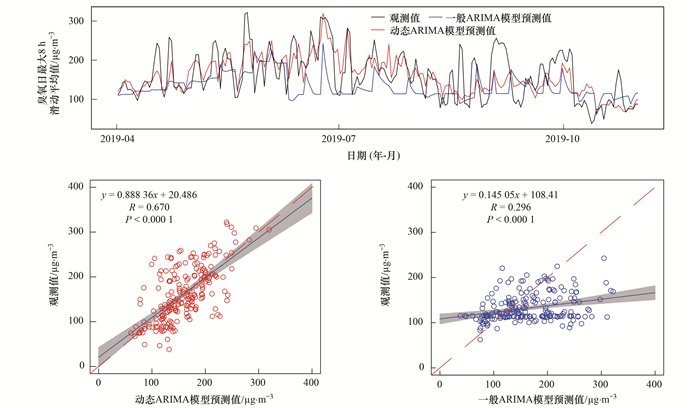
|
图 7 上甸子站一般ARIMA模型和动态ARIMA模型的预报结果 Fig. 7 Forecasting results of normal ARIMA model and dynamic ARIMA model at the SDZ site |
利用上甸子站点2015~2019年臭氧日最大8 h滑动平均值进行ARIMA建模预测分析表明, 加入了日最高气温及其二次项作为协变量的动态ARIMA模型对臭氧日最大8 h滑动平均值具有较好的预报效果.本研究进一步比较分析了动态ARIMA模型在不同预报时长(3 d、7 d、15 d和1个月)条件下模型预报性能表现.结果表明, 动态ARIMA模型在中长期(3~15 d)预报性能表现较为稳定, 观测值和预测值之间的相关系数在0.617~0.670之间(表 4).因此, 动态ARIMA模型可以用于臭氧日最大8 h滑动平均值中长期的预报.
|
|
表 4 动态ARIMA模型不同预报时长模型效果评价1) Table 4 Evaluation of dynamic ARIMA model for different forecasting durations |
2.3.3 动态ARIMA模型预报普适性检验
为了检验动态ARIMA模型在京津冀地区臭氧中长期预报中的空间普适性, 利用保定和天津站点2015~2019年观测数据进行了7 d臭氧日最大8 h滑动平均值预报模型空间适用性检验.和上甸子站点的结果类似, 未考虑日最高气温影响的一般ARIMA模型在保定和天津站点臭氧日最大8 h滑动均值预报中, 观测值和预测值的相关系数R分别为0.454和0.455, 而加入日最高气温及二次项作为协变量的动态ARIMA模型在保定和天津站点观测值和预报值的相关系数R可以提高到0.748和0.723(图 8).表明该动态ARIMA模型在京津冀地区臭氧中长期预报中具有较好的稳定性和空间普适性.
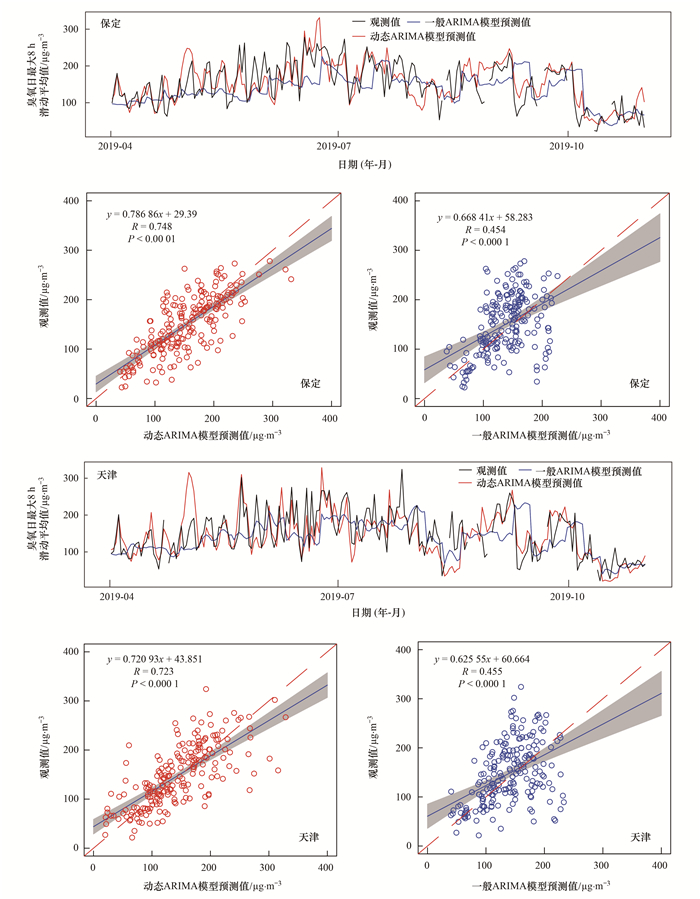
|
图 8 保定站和天津站一般ARIMA模型和动态ARIMA模型的预报结果 Fig. 8 Forecasting results of normal ARIMA model and dynamic ARIMA model at the Baoding site and the Tianjin site |
(1) 季节性ARIMA模型可以充分考虑具有季节变化的污染物的变化特征, 可用于臭氧月均值长期预报.
(2) 动态ARIMA模型在臭氧中长期预报中优势突出, 研究进一步验证了日最高气温是影响臭氧日最大8 h浓度的关键因素, 因此, 在加入了日最高气温及二次项最为协变量以后, 臭氧日最大8 h滑动平均值的预报效果得到了很大提升, 预测值和观测值的相关系数由0.296~0.455提升至0.670~0.748, RMSE得到了有效降低, 尤其是对于臭氧浓度高值的模拟偏差得到了有效控制.
(3) 动态ARIMA模型对臭氧日最大8 h滑动平均值3~15 d的中长期预报效果较为理想, 且在多个站点都取得了很好的预报效果, 因此该方法是臭氧日最大8 h浓度中长期预报的稳定性和普适性方法.
| [1] | Liu Y M, Wang T. Worsening urban ozone pollution in China from 2013 to 2017-part 1:the complex and varying roles of meteorology[J]. Atmospheric Chemistry and Physics, 2020, 20(11): 6305-6321. DOI:10.5194/acp-20-6305-2020 |
| [2] | Canella R, Borriello R, Cavicchio C, et al. Tropospheric ozone effects on chlorine current in lung epithelial cells: an electrophysiological approach[J]. Free Radical Biology and Medicine, 2016, 96: S58-S59. |
| [3] | Feng Z Z, Hu E Z, Wang X K, et al. Ground-level O3 pollution and its impacts on food crops in China: a review[J]. Environmental Pollution, 2015, 199: 42-48. DOI:10.1016/j.envpol.2015.01.016 |
| [4] |
余益军, 孟晓艳, 王振, 等. 京津冀地区城市臭氧污染趋势及原因探讨[J]. 环境科学, 2020, 41(1): 106-114. Yu Y J, Meng X Y, Wang Z, et al. Driving factors of the significant increase in surface ozone in the Beijing-Tianjin-Hebei region, China, during 2013-2018[J]. Environmental Science, 2020, 41(1): 106-114. DOI:10.13227/j.hjkx.201905222 |
| [5] | 陆克定, 张远航, 苏杭, 等. 珠江三角洲夏季臭氧区域污染及其控制因素分析[J]. 中国科学: 化学, 2010, 40(4): 407-420. |
| [6] | Lu K D, Guo S, Tan Z F, et al. Exploring atmospheric free-radical chemistry in China: the self-cleansing capacity and the formation of secondary air pollution[J]. National Science Review, 2019, 6(3): 579-594. DOI:10.1093/nsr/nwy073 |
| [7] | Wang T, Xue L K, Brimblecombe P, et al. Ozone pollution in China: a review of concentrations, meteorological influences, chemical precursors, and effects[J]. Science of the Total Environment, 2017, 575: 1582-1596. DOI:10.1016/j.scitotenv.2016.10.081 |
| [8] | Worden H M, Bowman K W, Worden J R, et al. Satellite measurements of the clear-sky greenhouse effect from tropospheric ozone[J]. Nature Geoscience, 2008, 1(5): 305-308. DOI:10.1038/ngeo182 |
| [9] | Monks P S, Archibald A T, Colette A, et al. Tropospheric ozone and its precursors from the urban to the global scale from air quality to short-lived climate forcer[J]. Atmospheric Chemistry and Physics, 2015, 15(15): 8889-8973. DOI:10.5194/acp-15-8889-2015 |
| [10] | Avnery S, Mauzerall D L, Liu J F, et al. Global crop yield reductions due to surface ozone exposure: 1. year 2000 crop production losses and economic damage[J]. Atmospheric Environment, 2011, 45(13): 2284-2296. DOI:10.1016/j.atmosenv.2010.11.045 |
| [11] |
徐晓斌, 林伟立. 卫星观测的中国地区1979-2005年对流层臭氧变化趋势[J]. 气候变化研究进展, 2010, 6(2): 100-105. Xu X B, Lin W L. 1979-2005 trends of tropospheric ozone over China based on the satellite data[J]. Advances in Climate Change Research, 2010, 6(2): 100-105. DOI:10.3969/j.issn.1673-1719.2010.02.005 |
| [12] | Fu Y, Liao H, Yang Y. Interannual and decadal changes in tropospheric ozone in China and the associated chemistry-climate interactions: a review[J]. Advances in Atmospheric Sciences, 2019, 36(9): 975-993. DOI:10.1007/s00376-019-8216-9 |
| [13] | Lu X, Hong J Y, Zhang L, et al. Severe surface ozone pollution in China: a global perspective[J]. Environmental Science & Technology Letters, 2018, 5(8): 487-494. |
| [14] | Ding A J, Wang T, Thouret V, et al. Tropospheric ozone climatology over Beijing: analysis of aircraft data from the MOZAIC program[J]. Atmospheric Chemistry and Physics, 2008, 8(1): 1-13. DOI:10.5194/acp-8-1-2008 |
| [15] |
陈鹏飞, 张蔷, 权建农, 等. 北京地区臭氧时空分布特征的飞机探测研究[J]. 环境科学, 2012, 33(12): 4141-4150. Chen P F, Zhang Q, Quan J N, et al. Temporal and spatial distribution of ozone concentration by aircraft sounding over Beijing[J]. Environmental Science, 2012, 33(12): 4141-4150. |
| [16] |
邓涛, 吴兑, 邓雪娇, 等. 珠江三角洲一次典型复合型污染过程的模拟研究[J]. 中国环境科学, 2012, 32(2): 193-199. Deng T, Wu D, Deng X J, et al. Simulation of a typical complex pollution process over Pearl River Delta area[J]. China Environmental Science, 2012, 32(2): 193-199. DOI:10.3969/j.issn.1000-6923.2012.02.001 |
| [17] | Xu Z N, Huang X, Nie W, et al. Impact of biomass burning and vertical mixing of residual-layer aged plumes on ozone in the Yangtze River Delta, China: a tethered-balloon measurement and modeling study of a multiday ozone episode[J]. Journal of Geophysical Research: Atmospheres, 2018, 123(20): 11786-11803. DOI:10.1029/2018JD028994 |
| [18] | Wang T, Ding A J, Gao J, et al. Strong ozone production in urban plumes from Beijing, China[J]. Geophysical Research Letters, 2006, 33(21). DOI:10.1029/2006GL027689 |
| [19] | Ma Z Q, Xu J, Quan W J, et al. Significant increase of surface ozone at a rural site, north of eastern China[J]. Atmospheric Chemistry and Physics, 2016, 16(6): 3969-3977. DOI:10.5194/acp-16-3969-2016 |
| [20] |
安俊琳, 王跃思, 朱彬. 主成分和回归分析方法在大气臭氧预报的应用——以北京夏季为例[J]. 环境科学学报, 2010, 30(6): 1286-1294. An J L, Wang Y S, Zhu B. Principal component and multiple regression analysis predicting ozone concentrations: case study in summer in Beijing[J]. Acta Scientiae Circumstantiae, 2010, 30(6): 1286-1294. |
| [21] |
陈亚玲, 赵智杰. 基于小波变换与传统时间序列模型的臭氧浓度多步预测[J]. 环境科学学报, 2013, 33(2): 339-345. Chen Y L, Zhao Z J. A multi-step-ahead prediction of ozone concentration using wavelet transform and traditional time series model[J]. Acta Scientiae Circumstantiae, 2013, 33(2): 339-345. |
| [22] |
朱佳, 王振会, 金天力, 等. 基于小波分解和最小二乘支持向量机的大气臭氧含量时间序列预测[J]. 气候与环境研究, 2010, 15(3): 295-302. Zhu J, Wang Z H, Jin T L, et al. Combination of wavelet decomposition and least square support vector machine to forcast atmospheric ozone content time series[J]. Climatic and Environmental Research, 2010, 15(3): 295-302. DOI:10.3878/j.issn.1006-9585.2010.03.09 |
| [23] |
李梓铭, 赵秀娟, 孙兆彬, 等. 基于相似集合预报技术的臭氧预报释用研究[J]. 中国环境科学, 2020, 40(2): 475-484. Li Z M, Zhao X J, Sun Z B, et al. Research on the interpretation and correction of numerical ozone forecast based on analog ensemble[J]. China Environmental Science, 2020, 40(2): 475-484. DOI:10.3969/j.issn.1000-6923.2020.02.002 |
| [24] | 黄文杰, 曹鸿兴, 顾岚, 等. 时间序列的ARIMA季节模型在长期预报中的应用[J]. 科学通报, 1980, 25(22): 1030-1032. |
| [25] | 王燕. 时间序列分析: 基于R[M]. 北京: 中国人民大学出版社, 2015. |
| [26] | Hyndman R J, Athanasopoulos G. Forecasting: principles and practice[M]. (2nd edition). Melbourne, Australia: OTexts, 2018. |
| [27] | Box G E P, Jenkins G M. Time series analysis: forecasting and control[M]. San Francisco: Holden-Day, 1970. |
| [28] | Gu Y X, Li K, Xu J M, et al. Observed dependence of surface ozone on increasing temperature in Shanghai, China[J]. Atmospheric Environment, 2020, 221. DOI:10.1016/j.atmosenv.2019.117108 |
| [29] | Pu X, Wang T J, Huang X, et al. Enhanced surface ozone during the heat wave of 2013 in Yangtze River Delta region, China[J]. Science of the Total Environment, 2017, 603-604: 807-816. DOI:10.1016/j.scitotenv.2017.03.056 |
| [30] | Gao Y, Zhang L, Zhang G, et al. The climate impact on atmospheric stagnation and capability of stagnation indices in elucidating the haze events over north China plain and northeast China[J]. Chemosphere, 2020, 258. DOI:10.1016/j.chemosphere.2020.127335 |
 2021, Vol. 42
2021, Vol. 42


