环境科学  2021, Vol. 42 Issue (6): 2769-2777   PDF    
引用本文
荣易, 秦成新, 杜鹏飞, 孙傅. 基于模型研究质量评价的SWAT模型参数取值特征分析[J]. 环境科学, 2021, 42(6): 2769-2777.
RONG Yi, QIN Cheng-xin, DU Peng-fei, SUN Fu. Characteristic Analysis of SWAT Model Parameter Values Based on Assessment of Model Research Quality[J]. Environmental Science, 2021, 42(6): 2769-2777.
基于模型研究质量评价的SWAT模型参数取值特征分析
荣易, 秦成新, 杜鹏飞, 孙傅     
清华大学环境学院, 北京 100084
收稿日期: 2020-10-28; 修订日期: 2020-11-25
基金项目: 国家水体污染控制与治理科技重大专项（2017ZX07301006002）；国家自然科学基金项目（51878372）
作者简介: 荣易(1995~), 男, 博士研究生, 主要研究方向为环境系统分析建模, E-mail: y-rong17@mails.tsinghua.edu.cn
通信作者: 孙傅, E-mail: sunfu@tsinghua.edu.cn
摘要: SWAT模型是目前我国应用最为广泛的流域水环境模型之一.由于该模型拥有分布式参数并且基于美国环境特征建立，确定合理的和符合我国流域环境特征的参数取值是模型应用中的关键工作.有研究通过总结现有报告的参数取值，为模型本地化应用提供参数取值参考，但这些研究忽略了其中SWAT模型研究质量之间的差异，也未考虑参数取值的非均匀性以及极端值的影响，因而研究结果的实用性不佳.建立了综合考虑模型建立、参数率定和验证、模拟效果的SWAT模型研究质量评价指标体系，对中国知网收录的2015~2017年发表的428篇SWAT模型研究文献开展定量评价并筛选高可信度文献.基于高可信度文献报告的SWAT模型参数取值，分析了15个涉及水文、泥沙和水质过程模拟的参数取值特征，包括参数取值分布特征及其在不同地理区域间的差异，以及参数率定值与默认值的偏差等.研究表明，在筛选得到的129篇高可信度文献中，SWAT模型应用整体上更加规范，且具有较好的区域代表性；15个模型参数在我国流域的取值分布具有正偏态、负偏态等不同特征，其中4个参数在我国不同地理区域的取值分布存在显著差异，12个参数在我国流域的取值明显偏离默认值.基于模型参数取值特征，以置信区间的形式给出了SWAT模型在我国本地化应用的参数取值建议，并针对不同数据条件下的模型应用提出了参数取值建议.
关键词: SWAT模型      指标体系      高可信度文献      参数取值      地理区域      置信区间     
Characteristic Analysis of SWAT Model Parameter Values Based on Assessment of Model Research Quality
RONG Yi , QIN Cheng-xin , DU Peng-fei , SUN Fu     
School of Environment, Tsinghua University, Beijing 100084, China
Abstract: The soil and water assessment tool (SWAT) model is currently one of the most widely used watershed models in China. Since the model has been developed with distributed parameters and is customized to satisfy the environmental characteristics of the U.S.A., determining appropriate parameter values that reflect local features for model application in China is crucial. Some studies have proposed parameter values for the SWAT model by summarizing reported values in the literature; however, these studies neither differentiate the literature with respect to its quality nor consider non-uniformity in parameter values and the impact of extreme values. To address this, an indicator system for assessing the quality of SWAT model research was established, taking into account the process of model development, parameter calibration, and model validation as well as model performance. This screening approach was applied to a total of 428 journal articles on SWAT model research published between 2015 and 2017 were retrieved from the China National Knowledge Infrastructure database. The reported values of 15 model parameters involved in hydrology and sediment and nutrient simulation were extracted from highly credible articles and analysed in terms of statistical distributions, differences among geographic regions, and discrepancies between calibrated and default values. Results showed that the 129 highly credible journal articles screened generally followed good modelling practice and consisted of case studies from different regions across China. The statistical distributions of the 15 model parameters derived from the SWAT model studies exhibited a range of features including positive and negative skewness, and those of 4 parameters showed significant differences among regions where the watersheds are located. Furthermore, the calibrated values of 12 out of 15 parameters were significantly different from their default values. Considering the statistical characteristics of these model parameters, recommended parameter values for SWAT model application in China are proposed in the form of confidence intervals, and specific suggestions are also provided based on data availability.
Key words: SWAT model      indicator system      highly credible literature      parameter value      geographic region      confidence interval     

SWAT(soil and water assessment tool)模型是目前我国应用最为广泛的流域水环境模型之一, 并且近年来相关应用研究的数量不断增加[1].作为分布式流域水环境模型, SWAT模型拥有大量参数, 其中大部分参数具有明确的物理意义和特定的取值范围.同时, 由于SWAT模型由美国农业部开发, 很多模型参数的默认取值源自美国实际观测或经验, 直接移用到我国可能导致偏差, 例如文献[2]发现SWAT模型中使用的径流曲线数经验对照表在我国并不适用.因此, 在SWAT模型的应用研究中, 应确保模型参数取值符合物理规律及应用流域特征[3].

针对SWAT模型参数取值合理性与本地化的要求, 同时考虑到模型参数众多的实际情况, 目前多数研究采用了先识别灵敏参数、而后仅率定灵敏参数的方法[4~6].然而, 现有的参数灵敏度分析方法多是基于大规模参数采样和模型计算的, 仍然需要耗费大量时间, 一定程度上影响了模型应用实践.为解决这一问题, 有研究通过总结已有文献的参数取值特征[7~11], 为模型本地化应用提供参数取值参考, 提高模型参数率定效率.例如, 文献[7]基于我国七大水系流域的600个应用案例, 总结提出了ESCO和ALPHA_BF等5个模型参数的取值建议.但是, 这些参数的本地化取值建议在实际应用中还存在一定局限.一方面, 这些取值建议所依据的部分案例存在观测数据时间序列较短和参数取值超出理论范围等问题[12], 由此得到的参数取值值得存疑, 如果不加甄别地用于分析参数取值特征, 则可能出现偏差.另一方面, 现有研究提供的模型参数本地化取值建议仅以上下界表征参数取值范围, 无法体现参数在此区间内的概率分布情况, 且受极端值影响较大, 降低了参数取值建议的实用性.

本文针对SWAT模型参数取值特征研究中存在的上述问题, 建立了SWAT模型研究质量评价指标体系, 对2015~2017年公开发表的SWAT模型在我国流域应用的文献进行评价, 并利用筛选得到的高可信度文献开展模型参数取值特征分析, 基于分析结果提出SWAT模型在我国本地化应用的参数取值建议.

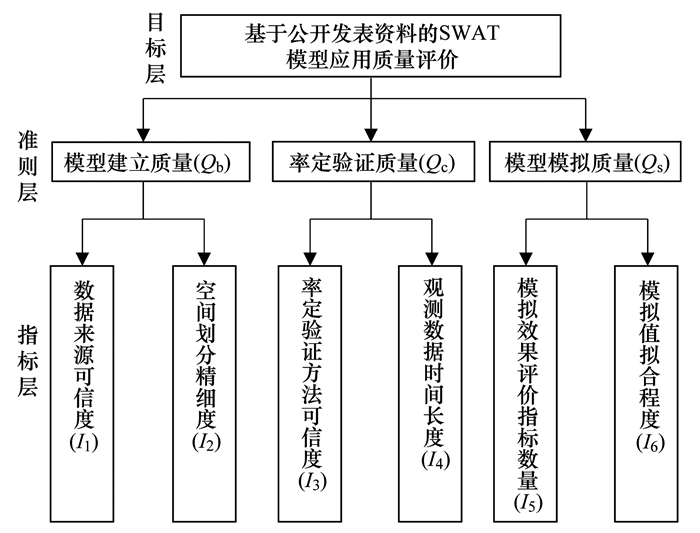
1 材料与方法 1.1 SWAT模型研究质量评价

本文依据文献[12]提出的SWAT模型评估验证过程评价方法, 同时考虑到公开发表文献中信息的可获得性, 建立了如图 1所示的由模型建立质量、率定验证质量和模型模拟质量这3个准则及其相应的6个指标构成的SWAT模型研究质量评价指标体系.利用该指标体系, 对文献[12]收集的2015~2017年公开发表的428篇SWAT模型研究文献的研究质量开展定量评价, 并由此筛选高可信度文献.

图 1 SWAT模型研究质量评价指标体系 Fig. 1 Quality assessment indicators for SWAT model studies

SWAT模型需要流域数字高程模型(DEM)、土地利用分布、土壤分布、气象和水文水质等基础数据, 数据来源可信度(I1)指标要求这些数据可溯源, 即文献应明确描述数据来源.该指标赋值规则如式(1)所示:

(1)

应用SWAT模型时, 子流域划分数量会影响模型模拟效果[13], 因此空间划分精细度(I2)指标要求文献对研究流域的空间划分水平合理.总结文献[14~17]并考虑到较小流域无需划分过多数量的子流域, 该指标赋值规则如式(2)所示:

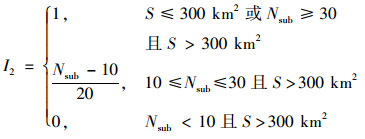
(2)

式中, S为文献中研究流域的面积, Nsub为子流域划分数量.若文献未报告子流域划分数量, 则I2为0.

模型参数率定和验证是提高模型可靠性的关键步骤, 因此率定验证方法可信度(I3)指标要求文献明确报告所使用的率定和验证方法.该指标赋值规则如式(3)所示:

(3)

SWAT模型通常用于较长时间尺度的流域水文水质模拟, 为保证模型在不同水文条件下均有良好的模拟表现, 应尽可能使用长时间序列的观测数据开展模型率定和验证.基于已有研究总结[18~20], 观测数据时间长度(I4)指标要求文献中用于SWAT模型率定和验证的观测数据时间长度合计不少于8 a.该指标赋值规则如式(4)所示:

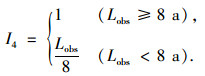
(4)

式中, Lobs为观测数据时间长度.

现有文献通常从趋势拟合效果(如决定系数)、均值拟合效果(如百分比偏差)和峰值拟合效果(如纳什效率系数)等3方面对SWAT模型模拟效果进行评价.由于单一种类指标无法全面表征拟合程度[21], 因此模拟效果评价指标数量(I5)指标要求文献应至少使用上述3类指标评价SWAT模型的模拟能力.该指标赋值规则如式(5)所示:

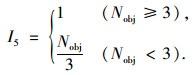
(5)

式中, Nobj为模拟效果评价指标类型的数量.

模拟值拟合程度(I6)指标要求采用不同的模拟效果评价指标时, SWAT模型的模拟值和观测值均能够较好地吻合.基于Moriasi等[22]总结的常用评价指标取值与模型模拟能力的评价标准, 该指标赋值规则如式(6)所示:

(6)

式中, NSE为变量拟合纳什效率系数值, R2为变量拟合决定系数值, PBIAS为变量拟合百分比误差值.

由于不同研究的目标不同, 其关注的模拟变量也不同, 此外不同流域的监测点位数量也存在差异, 这些难以形成统一标准, 因此本研究不将模拟变量数量和观测点位数量纳入评价.当文献中报告多模拟变量和多点位模拟结果时, 本研究选择水文观测数据(通常为流量)模拟效果最差的结果作为评价依据.

根据上述规则计算得到全部428篇文献的6个指标值后, 使用熵权法[23]确定各个指标的权重, 以避免主观赋权可能造成的经验性偏差.各文献研究质量的最终得分如式(7)所示:

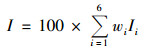
(7)

式中, I为最终得分, wi为第i项指标权重, Ii为第i项指标值.将各文献研究质量的最终得分从高到低排序, 选取其中排名前30%的文献认定为高可信度文献, 基于高可信度文献中SWAT模型参数取值开展后续研究.

1.2 SWAT模型参数取值特征分析

将筛选出的高可信度文献按照其研究流域在我国所处的地理区域(即西北地区、北方地区、南方地区和青藏地区)分类, 整理得到SWAT模型在各地理区域应用时的参数典型取值, 分析不同区域之间参数取值分布的差异、各区域内部参数取值分布的特征及其与参数默认值的偏差程度, 在此基础上提出SWAT模型本地化应用的参数取值建议.

1.2.1 区域间参数取值分布差异

由于不同地理区域气候和地理条件不同, SWAT模型参数取值分布可能存在整体差异.本研究使用两样本Kolmogorov-Smirnov(K-S)检验评价不同区域之间的模型参数取值分布是否存在显著差异, 统计量DK-S代表两经验分布间距离的最大值, 可由式(8)计算:

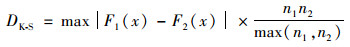
(8)

式中, F1(x)和F2(x)分别为两个区域参数取值样本的经验分布, n1和n2为两个样本的样本数量.通过查表可知DK-S在自由度f下的显著度水平P, 通常认为P < 0.05时两样本的经验分布存在显著差异.

1.2.2 区域内参数取值分布特征

为了避免简单地以取值范围表示SWAT模型参数取值特征、忽视参数在取值范围内分布不均匀的特点, 本研究计算各区域内模型参数取值分布的偏度S和峰度K, 由此分析参数取值分布特征.两个指标的计算方法如式(9)和(10)所示:

(9)
(10)

式中, n为参数取值样本数量, 为样本平均数, xi为第i个样本值.

1.2.3 参数率定值与默认值的偏差程度

为了分析SWAT模型参数默认值是否可能直接移用至我国流域, 本研究使用箱式图定性比较模型参数取值与默认值的偏差程度, 观察是否存在整体高于或低于默认值的情况以及参数取值在默认值附近的密集程度.

2 结果与讨论 2.1 高可信度文献筛选

由熵权法计算得到的SWAT模型研究质量评价各指标的权重取值如表 1所示, 其中空间划分精细度和率定验证方法可信度两项指标的权重较大, 说明现有文献在这两个指标上的得分较为分散, 是体现研究质量差别的主要指标.数据来源可信度和模拟值拟合程度两项指标的权重相对较低, 这是由于现有文献中数据的可溯源性以及模型的模拟效果总体较好[12], 例如纳什效率系数通常高于0.5.

表 1 SWAT模型研究质量评价指标权重 Table 1 Weighting of quality assessment indicators for SWAT model studies

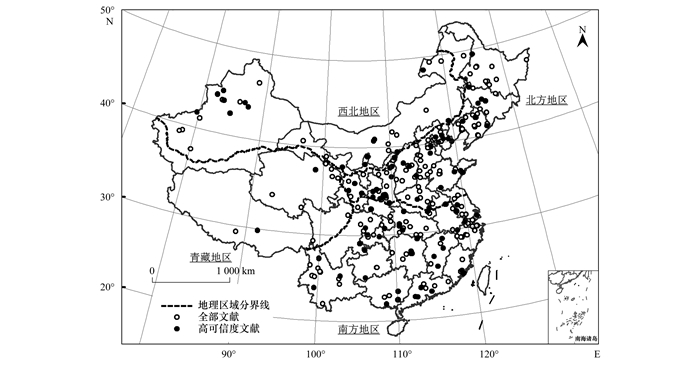
428篇文献最终得分的最高值、最低值、平均值和中位数分别为100、0、67.32和71.21, 而按得分排名前30%筛选得到的129篇高可信度文献的得分均超过90, 说明高可信度文献的SWAT模型研究整体上更加规范.图 2给出了全部文献和高可信度文献研究流域位置的分布, 从中可以看出, 虽然4个地理区域的文献数量存在差异, 但高可信度文献与全部文献的空间分布较为相似, 因此筛选得到的高可信度文献具有较好的区域代表性.

图 2 被评价文献中研究流域的位置分布示意 Fig. 2 Distribution of the studied watersheds in the reviewed journal articles

2.2 SWAT模型参数取值特征分析

整理高可信度文献中报告的SWAT模型参数取值, 选定控制流域不同水文水质过程且参数取值报告较多的15个参数进行分析, 包括: ALPHA_BF、CN2、CH_K2、CH_N2、CANMX、ESCO、EPCO、GW_REVAP、GW_DELAY、SURLAG、SOL_AWC、SOL_K、SPCON、SPEXP和NPERCO.这些参数控制了产流(CN2)、汇流(SURLAG)、蒸散发(CANMX、ESCO、EPCO)、土壤水(SOL_AWC、SOL_K)、地下水(ALPHA_BF、GW_REVAP、GW_DELAY)、河道(CH_K2、CH_N2)等水文过程以及泥沙(SPCON、SPEXP)和水质(NPERCO)过程的模拟.由于青藏地区高可信度文献数量较少, 不足以开展统计分析, 因此下文只对西北、北方和南方这3个地区的参数取值特征进行分析.

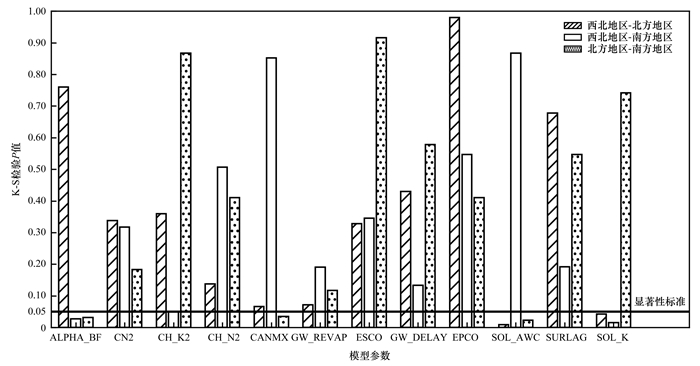
2.2.1 不同区域参数取值分布差异分析

图 3所示为不同地理区域间SWAT模型参数取值两样本K-S检验P值结果, 由于控制泥沙和水质过程的参数取值报告总数较少, 故不做区域间差异分析.从中可以看出, ALPHA_BF、CANMX、SOL_AWC和SOL_K等4个参数的取值分布在部分区域间存在显著差异.

图 3 不同地理区域间SWAT模型参数取值分布的两样本K-S检验P值 Fig. 3 Two-sample K-S test P values for SWAT model parameters between different regions

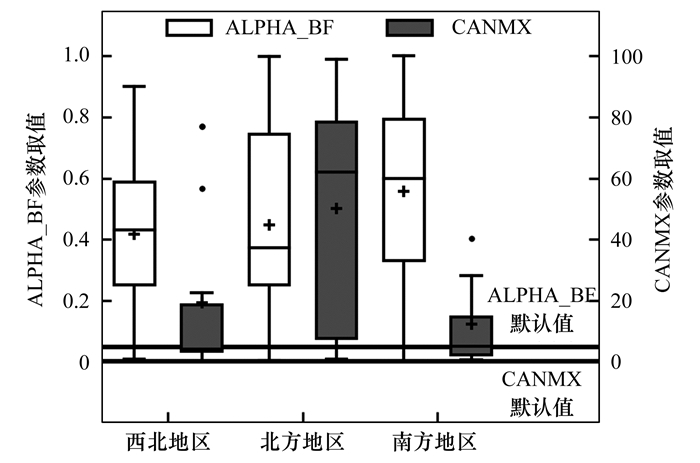
从图 4所示的参数取值分布可以看出, 南方地区ALPHA_BF取值的平均数和中位数均明显高于西北和北方地区, 而北方地区的CANMX明显高于西北和南方地区.ALPHA_BF为基流衰退系数, 控制地下水进入河道的速率; ALPHA_BF越大, 基流越平稳.由于南方地区属于湿润区, 降雨相对较多, 土壤长期处于高含水量状态, 地下水径流相对降雨量较少的北方和西北地区更为稳定[9], 因而ALPHA_BF取值较高.CANMX为植物冠层最大持水量, 控制植物对降雨的截流过程; CANMX越大, 降落到地表的水分越少, 径流量越小.由于北方地区以阔叶林为主, 树冠截流能力较强, 而且部分研究流域处在水库附近[24, 25], 多为流域上游, 植被覆盖较好, 两者共同导致CANMX参数取值较高.

图 4 参数ALPHA_BF和CANMX的默认值及其在不同地理区域的取值分布 Fig. 4 Default values of ALPHA_BF and CANMX and their statistical distributions among different regions

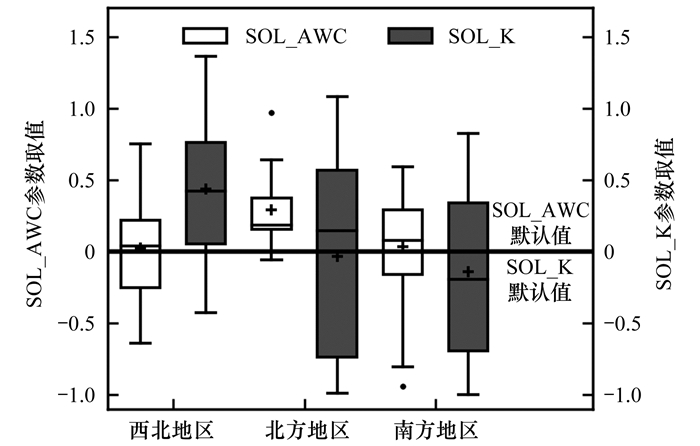
参数SOL_AWC和SOL_K随土壤种类而变化, 调整参数取值时通常设置为与调整前参数取值的相对变化率, 文献报告值也均为相对变化率.SOL_AWC为土壤持水度, 控制土壤水与河道及地下水的交互; SOL_AWC越大, 土壤可容纳水分越多, 径流量越小.SOL_K为土壤饱和水力传导率, 控制地表水渗入土壤的速率; SOL_K越大, 土壤渗透性越强.图 5为不同地理区域SOL_AWC和SOL_K取值分布, 从中可以看出, 西北地区率定后的SOL_K取值明显高于初始值, 平均约为初始值的1.5倍, 而北方地区率定后的SOL_AWC取值也高于初始值约30%.在SWAT模型应用中, SOL_AWC和SOL_K的初始值通常基于土壤数据库中的粒径数据进行计算, 而SWAT模型默认的粒径数据为美国标准, 与国内不同, 需进行转换[26].这一转换过程可能导致用于计算的土壤粒径组成与实际情况不符, 从而造成参数初始值与率定值之间的偏差.

图 5 参数SOL_AWC和SOL_K的默认值及其在不同地理区域的取值分布 Fig. 5 Default values of SOL_AWC and SOL_K and their statistical distributions among different regions

2.2.2 区域内参数取值分布特征分析

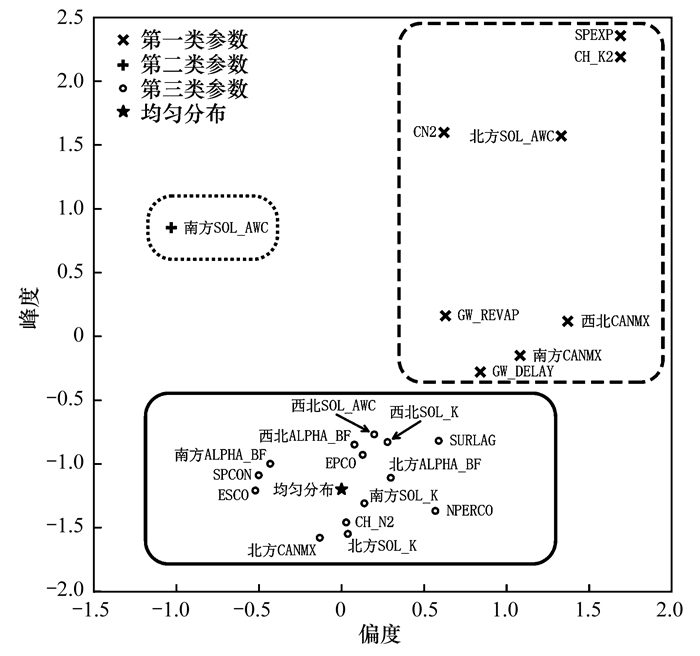
图 6为不同地理区域SWAT模型参数取值分布的偏度和峰度计算结果, 作为比较, 标准均匀分布的偏度和峰度也列在其中.根据图中各个参数与均匀分布的相对位置, 可将所有参数分为3类.第一类参数取值分布的峰度和偏度均远大于均匀分布, 包括北方地区的SOL_AWC、西北和南方地区的CANMX以及全国范围内的CN2、SPEXP、CH_K2、GW_REVAP和GW_DELAY等参数.第二类参数的峰度远大于均匀分布, 但偏度远小于均匀分布, 仅有南方地区SOL_AWC一个参数.第三类参数的峰度和偏度均接近均匀分布, 包括第一和第二类参数之外的其他参数.

图 6 不同地理区域SWAT模型参数取值分布及均匀分布的偏度和峰度 Fig. 6 Skewness and kurtosis of SWAT model parameters in different regions in comparison with the uniform distribution

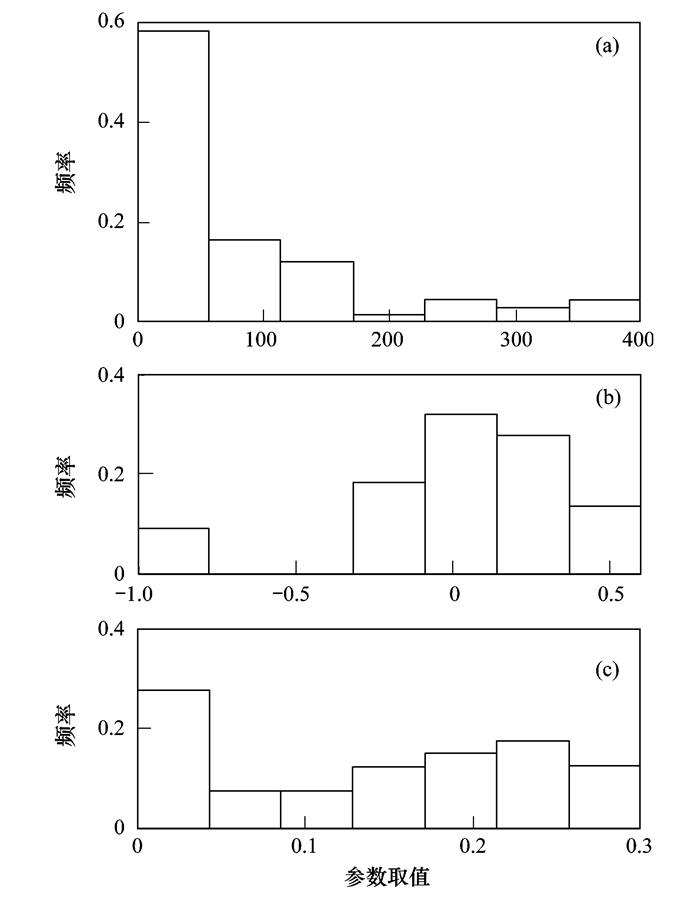
图 7以上述3类参数中的典型参数为例, 给出了其取值分布.从中可以看出, 第一类参数的取值分布呈现明显的正偏态, 大部分取值集中在最小值附近; 第二类参数呈现明显的负偏态, 大部分取值趋向于较大值; 第三类参数则呈现双峰或均匀分布, 没有明显的集中趋势.由于参数取值分布存在偏态, 在以最小值和最大值构成的取值范围内, 参数在某个区间内取值的概率较低.例如, 参数CH_K2的取值范围为[1.5, 394.9], 但落在[300, 394.9]区间的概率仅为4.5%, 而这个区间相当于取值范围的24.1%.如果采用置信区间的概念, 在参数率定时排除这一低概率区间, 则可以在保证一定置信水平的同时大幅缩小采样空间, 提高计算效率.

图 7 SWAT模型3类参数的取值分布 Fig. 7 Histograms of SWAT model parameters in three types

2.2.3 参数率定值与默认值的偏差程度

从图 4可以看出, SWAT模型在我国西北、北方和南方地区应用时, 率定得到的参数ALPHA_BF取值分布的第一四分位数均高于其默认值, 而参数CANMX的取值分布则明显偏离其默认值.类似地, 如图 5所示, 北方地区参数SOL_AWC和西北地区参数SOL_K取值分布的第一四分位数也均高于相应的默认值, 而其他地区这两个参数的取值分布则围绕其默认值, 高于默认值和低于默认值的概率相当.

图 8所示为其它11个取值分布在我国不同地理区域间无显著差异的SWAT模型参数的取值分布及其相应的默认值.从中可以看出, EPCO、CH_K2、CH_N2和SPCON等4个参数的取值分布明显偏离默认值, GW_REVAP、GW_DELAY、ESCO和SPEXP等4个参数的默认值或是低于率定值分布的第一四分位数、或是高于率定值分布的第三四分位数, SURLAG和NPERCO的率定值分布也有较高的概率高于其默认值, 而CN2取值分布则围绕默认值近似呈对称分布.

图 8 SWAT模型其它11个参数的取值分布及其默认值 Fig. 8 Default values and statistical distributions of the other 11 SWAT model parameters

综上, 在本研究的15个SWAT模型参数中, 12个参数在我国流域的率定值以较大概率偏离默认值, 因此默认值的适用性较差.而CN2、SOL_AWC和SOL_K在我国或其部分区域的取值分布与默认值相比不存在系统性偏差, 参数率定值高于或低于默认值的概率相当.但由于这3个参数在我国流域多属于灵敏参数[12], 因此也不宜直接使用默认值.

3 SWAT模型本地化应用的参数取值建议

如表 2所示, 基于上述分析, 本研究针对SWAT模型的15个参数提出本地化应用的取值建议.与文献[7]相比, 本研究基于参数取值特征分别以90%和75%置信区间的形式给出参数取值范围建议, 并根据三类不同的参数取值分布特点, 选择不同的方法计算置信区间: 第一类参数为右侧单侧置信区间, 第二类参数为左侧单侧置信区间, 而第三类参数为双侧置信区间.同时, 对于在不同地理区域间存在取值差异的参数, 分别给出不同区域的取值范围建议.

表 2 SWAT模型在中国应用的参数取值建议1) Table 2 Recommended parameter values for SWAT model application in China

在应用SWAT模型开展流域水环境模拟时, 如果研究流域的数据资料较为齐全, 有条件开展模型参数率定和验证, 那么表 2可为研究者提供参数先验分布取值范围的参考.如果研究流域数据资料缺乏, 特别是缺乏观测数据, 本研究亦可提供模型参数初始化的取值参考.例如, 对于CN2、研究流域位于西北和南方地区时的SOL_AWC等参数, 其默认值在表 2建议的取值范围内, 因此其初始化取值可选用默认值; 而对于ALPHA_BF、CANMX和SPCON等参数, 由于其默认值偏离表 2建议的取值范围, 其初始化取值可选用研究流域所在区域取值分布的中位数等.

4 结论

(1) SWAT模型研究质量评价结果表明, 从428篇文献中筛选得到的129篇高可信度文献的得分均超过90.高可信度文献的SWAT模型应用整体上更加规范, 且高可信度文献与全部文献的空间分布较为相似, 具有较好的区域代表性.

(2) 考察的15个SWAT模型参数中, 与地下水、土壤水和蒸散发过程相关的4个水文参数在我国不同地理区域的取值分布存在显著差异; 7个与地下水、土壤水、产流、蒸散发和河道过程相关的参数在我国及其部分区域的取值分布呈现明显的正偏态或负偏态; 在我国流域应用时, 全部15个参数均不宜直接使用模型默认值.

(3) 以90%和75%置信区间的形式给出了SWAT模型在我国本地化应用的参数取值建议, 并针对不同数据条件下的模型应用提出了参数取值建议.

参考文献
[1] 尤丽萍, 林雪儿, 林美娇, 等. 可视化知识图谱的中国SWAT模型研究趋势分析[J]. 武夷学院学报, 2019, 38(3): 33-39.
You L P, Lin X E, Lin M J, et al. An analysis of research trends of Chinese SWAT model based on visual knowledge map[J]. Journal of Wuyi University, 2019, 38(3): 33-39.
[2] Lian H S, Yen H, Huang J C, et al. CN-China: revised runoff curve number by using rainfall-runoff events data in China[J]. Water Research, 2020, 177. DOI:10.1016/j.watres.2020.115767
[3] Arnold J G, Moriasi D N, Gassman P W, et al. SWAT: model use, calibration, and validation[J]. Transactions of the ASABE, 2012, 55(4): 1491-1508. DOI:10.13031/2013.42256
[4] Wang Q R, Liu R M, Men C, et al. Temporal-spatial analysis of water environmental capacity based on the couple of SWAT model and differential evolution algorithm[J]. Journal of Hydrology, 2019, 569: 155-166. DOI:10.1016/j.jhydrol.2018.12.003
[5] Wang R, Yao Z J, Lei Y P. Modeling of soil available phosphorus surplus in an intensive wheat-maize rotation production area of the North China Plain[J]. Agriculture, Ecosystems & Environment, 2019, 269: 22-29.
[6] Hu J, Ma J, Nie C, et al. Attribution analysis of runoff change in Min-Tuo River Basin based on SWAT model simulations, China[J]. Scientific Reports, 2020, 10(1). DOI:10.1038/s41598-020-59659-z
[7] 王晓朋, 乔飞, 雷坤, 等. SWAT模型在我国的研究和应用进展[J]. 中国农村水利水电, 2015(5): 109-113.
Wang X P, Qiao F, Lei K, et al. Research on and application of SWAT model in China[J]. China Rural Water and Hydropower, 2015(5): 109-113. DOI:10.3969/j.issn.1007-2284.2015.05.027
[8] 高鑫. SWAT模型径流过程参数时空差异研究[D]. 福州: 福建师范大学, 2018.
Gao X. Spatial-temporal differences of hydrologic parameters in SWAT model[D]. Fuzhou: Fujian Normal University, 2018.
[9] 林炳青, 陈莹, 陈兴伟. SWAT模型水文过程参数区域差异研究[J]. 自然资源学报, 2013, 28(11): 1988-1999.
Lin B Q, Chen Y, Chen X W. A study on regional difference of hydrological parameters of SWAT model[J]. Journal of Natural Resources, 2013, 28(11): 1988-1999. DOI:10.11849/zrzyxb.2013.11.015
[10] Malagò A, Pagliero L, Bouraoui F, et al. Comparing calibrated parameter sets of the SWAT model for the Scandinavian and Iberian peninsulas[J]. Hydrological Sciences Journal, 2015, 60(5): 949-967.
[11] Daggupati P, Deb D, Srinivasan R, et al. Large-scale fine-resolution hydrological modeling using parameter regionalization in the Missouri River Basin[J]. Journal of the American Water Resources Association, 2016, 52(3): 648-666. DOI:10.1111/1752-1688.12413
[12] 荣易, 秦成新, 孙傅, 等. SWAT模型在我国流域水环境模拟应用中的评估验证过程评价[J]. 环境科学研究, 2020, 33(11): 2571-2580.
Rong Y, Qin C X, Sun B, et al. Assessment of evaluation process of SWAT model application in China[J]. Research of Environmental Sciences, 2020, 33(11): 2571-2580.
[13] 张雪松, 郝芳华, 程红光, 等. 亚流域划分对分布式水文模型模拟结果的影响[J]. 水利学报, 2004(7): 119-123, 128.
Zhang X S, Hao F H, Cheng H G, et al. Influence of subdivision of watershed on distributed hydrological model[J]. Journal of Hydraulic Engineering, 2004(7): 119-123, 128. DOI:10.3321/j.issn:0559-9350.2004.07.021
[14] 陈肖敏, 郭平, 彭虹, 等. 子流域划分对SWAT模型模拟结果的影响研究[J]. 人民长江, 2016, 47(23): 44-49.
Chen X M, Guo P, Peng H, et al. Influence of different sub-watershed division schemes on simulation results of SWAT model[J]. Yangtze River, 2016, 47(23): 44-49.
[15] 喻晓, 马孝义, 蔡朵朵. 基于SWAT模型的合理亚流域划分和径流模拟[J]. 中国农村水利水电, 2017(11): 20-25.
Yu X, Ma X Y, Cai D D. The reasonable sub-watershed delineation and runoff simulation based on SWAT model[J]. China Rural Water and Hydropower, 2017(11): 20-25. DOI:10.3969/j.issn.1007-2284.2017.11.005
[16] Jha M, Gassman P W, Secchi S, et al. Effect of watershed subdivision on SWAT flow, sediment, and nutrient predictions[J]. Journal of the American Water Resources Association, 2004, 40(3): 811-825. DOI:10.1111/j.1752-1688.2004.tb04460.x
[17] Fitzhugh T W, Mackay D S. Impacts of input parameter spatial aggregation on an agricultural nonpoint source pollution model[J]. Journal of Hydrology, 2000, 236(1-2): 35-53. DOI:10.1016/S0022-1694(00)00276-6
[18] Yapo P O, Gupta H V, Sorooshian S. Automatic calibration of conceptual rainfall-runoff models: sensitivity to calibration data[J]. Journal of Hydrology, 1996, 181(1-4): 23-48. DOI:10.1016/0022-1694(95)02918-4
[19] Huang Y C, Bardossy A. Impacts of data quantity and quality on model calibration: Implications for model parameterization in data-scarce catchments[J]. Water, 2020, 12(9). DOI:10.3390/w12092352
[20] Li C Z, Wang H, Liu J, et al. Effect of calibration data series length on performance and optimal parameters of hydrological model[J]. Water Science and Engineering, 2010, 3(4): 378-393.
[21] Jackson E K, Roberts W, Nelsen B, et al. Introductory overview: error metrics for hydrologic modelling-A review of common practices and an open source library to facilitate use and adoption[J]. Environmental Modelling & Software, 2019, 119: 32-48.
[22] Moriasi D N, Gitau M W, Pai N, et al. Hydrologic and water quality models: Performance measures and evaluation criteria[J]. Transactions of the ASABE, 2015, 58(6): 1763-1785. DOI:10.13031/trans.58.10715
[23] 邹志红, 孙靖南, 任广平. 模糊评价因子的熵权法赋权及其在水质评价中的应用[J]. 环境科学学报, 2005, 25(4): 552-556.
Zou Z H, Sun J N, Ren G P. Study and application on the entropy method for determination of weight of evaluating indicators in fuzzy synthetic evaluation for water quality assessment[J]. Acta Scientiae Circumstantiae, 2005, 25(4): 552-556. DOI:10.3321/j.issn:0253-2468.2005.04.022
[24] 尹军. 流域干旱还原理论与方法研究——以白洋淀流域为例[D]. 北京: 中国水利水电科学研究院, 2017.
Yin J. Research on drought reduction theory and method in basin-with Baiyangdian River basin as the case study[D]. Beijing: China Institute of Water Resources & Hydropower Research (IWHR), 2017.
[25] 张亚娟. 流域"源—汇"景观格局对河流氮磷影响的研究[D]. 天津: 天津师范大学, 2017.
Zhang Y J. Effects of landscape pattern of "source-sink" on the nitrogen and phosphorus in rivers[D]. Tianjin: Tianjin Normal University, 2017.
[26] 徐冬梅, 胡昊, 王文川, 等. SWAT模型土壤物理属性数据库本土化构建研究[J]. 华北水利水电大学学报(自然科学版), 2018, 39(1): 36-41.
Xu D M, Hu H, Wang W C, et al. Localization method for soil physical property database of SWAT model[J]. Journal of North China University of Water Resources and Electric Power (Natural Science Edition), 2018, 39(1): 36-41. DOI:10.3969/j.issn.1002-5634.2018.01.006