2. 湖南科技大学地理空间信息技术国家地方联合工程实验室, 湘潭 411201;
3. 中南大学地质资源与地质工程系, 长沙 410000;
4. 中南林业科技大学测绘工程系, 长沙 410000
2. National-Local Joint Engineering Laboratory of Geo-Spatial Information Technology, Hunan University of Science and Technology, Xiangtan 411201, China;
3. Department of Geological Engineering, Central South University, Changsha 410000, China;
4. Department of Surveying and Mapping Engineering, Central South University of Forest and Technology, Changsha 410000, China
改革开放以来, 粗放型经济发展模式在满足我国人民日益增长的物质文化需求的同时, 给我国生态环境带来了极为严峻的挑战.当前, 以细颗粒物(PM2.5)为特征的区域性大气污染问题尤为突出, 严重威胁着人民群众身体健康, 制约着社会经济可持续发展.有研究显示, 2013年中国近83%的人口暴露于PM2.5年均浓度高于空气质量二级阈值[《环境空气质量标准》(GB 3095-2012)]的污染环境中, PM2.5暴露导致约130万人过早死亡[1], 2017年全国PM2.5污染健康经济损失约占当年GDP的1.53%[2], 近十年来环境污染治理成本已达到GDP的10%[3].面临空前严峻的大气污染形势, 我国政府明确提出防治大气污染, 转变经济发展模式, 优化产业结构和布局、调整能源结构, 推行区域大气污染联合防治.
针对细颗粒物为特征的大气污染防治, 首先需要回答, 究竟有哪些因素与细颗粒物存在关联, 关联机制是否随时空发生变化, 如何变化.以这一系列问题为导向, 国内外学者已进行了大量研究, 较多研究集中于局地/区域空间尺度或较短时间跨度, 由于各区域的污染关联因素(自然因素或社会经济因素)呈现显著的时空变异性, 即不同区域在同一时期的关联机制各异, 同一区域关联机制亦随时间发生变化, 使得PM2.5关联分析结果存在明显的差异[4~12].此外, 从大气污染治理的角度看, 大气污染的外溢性引起治理责任界定模糊, 各自为政的方式会导致“搭便车”等问题, 只有相邻地区的联合和突破行政边界, 摸清大气污染潜在的关联机制, 形成污染治理合力才能有效地控制污染物的转移[13], 因此, 联合治理分区下PM2.5关联关系时空变异特征识别对有效大气污染联合治理具有重要的现实意义.然而, 我国虽然已成立京津冀与长三角区域大气污染防治小组, 但目前国家尺度上大气防治联合分区规模尚未成熟, 全国统筹的大气污染联合治理框架仍未形成[14, 15].国内学者虽然从不同的视角出发, 构建了大气污染联防联控划分方案, 但是, 划分策略不同与选择因素各异导致分区结果的不一致[16, 17].鉴于不同污染物的形成与关联机制存在差异[18~20], 基于不同的污染物构建的分区可能不尽相同, 故迫切需要针对当前细颗粒物造成的污染, 建立污染联合治理分区方案, 实现大气污染联合治理分区下PM2.5关联关系时空变异特征识别.
为此, 本文基于2000~2016年遥感反演的PM2.5数据与社会经济数据等, 利用地理时空加权回归模型, 识别334个地级市PM2.5关联关系的时空变异特征, 在此基础上, 针对国家尺度大气污染联合治理对区域性PM2.5关联关系识别的迫切需求, 建立以PM2.5为首要污染物的大气污染联合治理分区方案, 通过空间单元聚合分析不同PM2.5关联关系时空变异特征, 以期为区域大气污染联合防治提供有效的决策支撑信息.
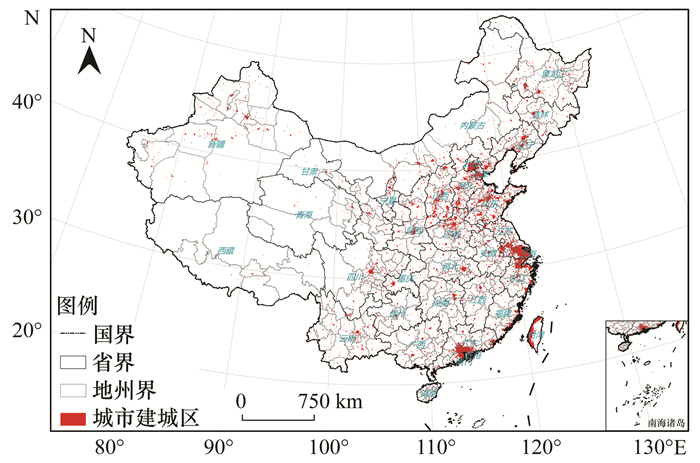
1 材料与方法 1.1 数据来源与处理本研究所采用的PM2.5数据来源于MODIS、MISR以及SeaWiFS气溶胶反演的全球2000~2016年年均PM2.5浓度格网数据集(https://beta.sedac.ciesin.columbia.edu), 空间分辨率为1km.考虑到城市是人类活动最为强烈的区域, 亦是PM2.5污染事件发生的主要区域, 本文以我国大陆地区334个地级市为初始的分析单元, 采用2000~2012年的DMSP/OLS以及2013~2016年NPP/VIIRS夜间灯光数据(https://ngdc.noaa.gov/)分别对每年城市建成区的范围进行提取[21], 图 1为提取2005年全国城市建成区的空间分布, 将各地级市范围内建成区包含格网中PM2.5浓度平均值设置为分析单元的PM2.5浓度值.自然因素主要包括:我国大陆地区607个气象站点记录2000~2016年的年平均气温、年降水量以及年平均相对湿度(数据来源于http://data.cma.cn).社会经济数据则直接来源于2000~2016年城市统计年鉴(http://www.stats.gov.cn), 主要包括:国内生产总值、第二产业生产总量、地区人口数量、SO2排放量和城市年用电量.
|
图 1 2005年我国城市建成区空间分布示意 Fig. 1 Spatial distribution of built-up areas of Chinese cities in 2005 |
本文以PM2.5为首要污染物, 综合考虑污染程度、地理位置、气象、地形和经济等因素建立大气污染联合治理分区方案[14].PM2.5污染严重的区域是治理主要关注点, 因此, 可将污染程度转化为污染中心地条件, 依据污染中心地条件识别不同类型污染区域, 进一步以重点区为分区的逻辑起点, 兼顾其它因素进行污染治理联合分区.地形与气象条件直接影响污染物扩散与输送, 同时该物理过程在空间的连续性决定了在风向路径上地理位置越邻近的地区越容易产生跨区污染问题, 故风向与地理邻近是区域划分的约束条件.此外, 城市经济联系度高的地区通常表现为政府、企业间强关联度, 此条件下联合治理效率高, 经济联系度应作为区域划分因素之一.城市i与j之间经济联系度Tij可利用空间交互模型进行测度, 其表达式如下:
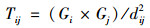
|
(1) |
式中, Gi与Gj表示城市i与j的经济总量, dij为城市间的空间距离.
基于上述分析可以定义大气污染防治分区方案:首先, 构建省份间空间邻近关系的0~1矩阵(有公共边界的省份定义为相邻, 元素值设为1, 否则为0), 并依据式(1)计算省份间社会经济关联距离矩阵;然后, 对各省份污染物浓度进行分级, 参考《环境空间质量标准》(GB 3095-2012)中PM2.5年平均浓度一、二级限值, 按照年平均浓度0~15、15~25、25~35、35~45与>45μg·m-3识别出污染轻微污染区、较轻度污染区、中度污染区、较重污染区与重度污染区;在此基础上, 以重度污染区为逻辑起点, 合并其风向路径上最大经济联系度的空间邻近单元, 依次对其它污染类型区域进行处理, 直到所有区域均被遍历一次.
1.2.2 地理空加权回归模型地理时空加权回归(geographically and temporally weighted regression, GTWR)是在经典地理加权回归的基础上, 通过构建时空依赖的局部模型对时空非平稳关系建模[22, 23].由于该模型能够较好地刻画变量间关系的时空变异, 近年来受到了广泛地关注与应用[24~26].GTWR模型的表达式为:
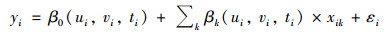
|
(2) |
式中, (ui, vi, ti)表示i个观测点(i=1, 2, …, n, n为观测样本数)的空间与时间位置信息, yi与xik分别为第i个观测点因变量与自变量, β0(ui, vi, ti)与βk(ui, vi, ti)分别表示第i个观测点所在位置回归模型的常数项与系数项, εi表示模型的随机误差项.回归系数的估计值可以表示为:
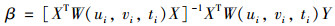
|
(3) |
式中, 权重W(ui, vi, ti)=diag(αi1, αi2, …, αin), αij为观测点j的样本权重.在对第i观测点对应模型的参数估计中, 通常假设:离观测点i时空距离越近的样本点j其重要性越大, 该点观测值对应的权重αij赋予较大的值, 而距离较远的观测点则被赋予较小的权值.此外, 考虑到空间与时间尺度效应的差异, GTWR在定义时空耦合距离基础上, 建立时空距离衰减函数来计算权重.
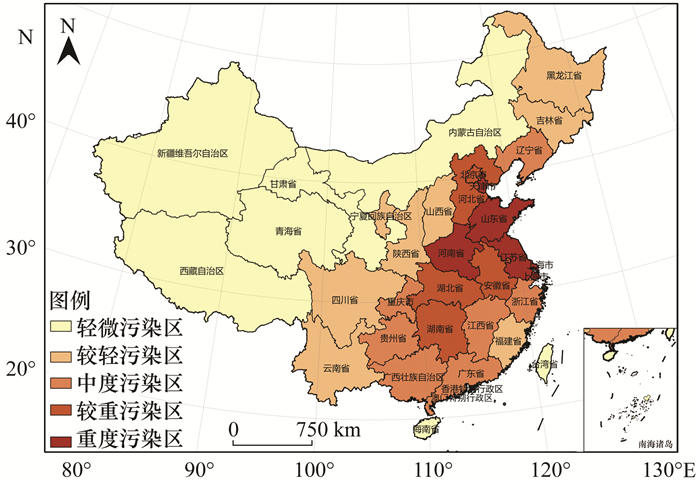
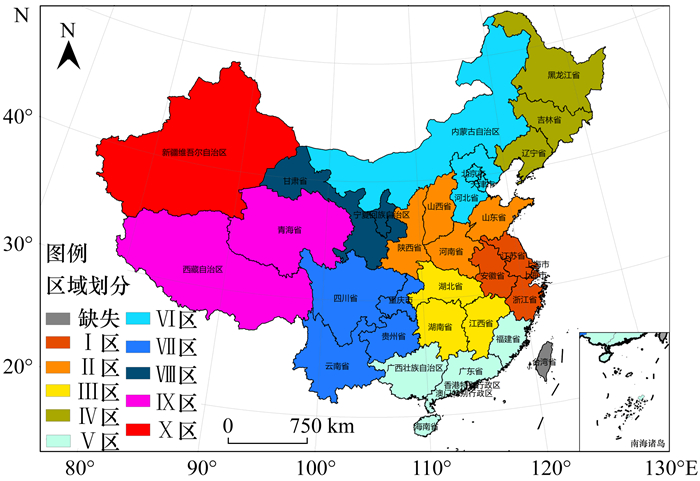
2 结果与讨论 2.1 PM2.5污染联合治理分区结果依据1.2.1节中大气污染防治分区方案, 首先, 基于空间拓扑关系判断省份间是否存在公共边, 构建描述空间邻近关系的0~1矩阵, 并计算省份间经济联系度;然后, 按照年平均浓度0~15、15~25、25~35、35~45与>45 μg·(m3)-1对2016年的PM2.5年平均浓度进行分级, 识别出轻微污染区、较轻度污染区、中度污染区、较重污染区与重度污染区(图 2).在此基础上, 通过合并风向路径上最大经济联系度的空间邻近单元, 最终得到10个联合治理区(图 3), 分别为:Ⅰ区苏皖沪浙、Ⅱ区陕晋豫鲁、Ⅲ区鄂湘赣、Ⅳ区黑吉辽、Ⅴ区桂粤闽琼、Ⅵ区京津冀蒙、Ⅶ区川渝滇黔、Ⅷ区宁甘、Ⅸ区青藏与Ⅹ区新疆.
|
图 2 全国PM2.5污染分级结果 Fig. 2 Graded results of PM2.5 pollution in China |
|
图 3 大气污染联合治理分区结果 Fig. 3 Results of zoning for air pollution regional linkage control and prevention |
采用GTWR对数据集进行建模分析, 可以得到334个地级市PM2.5关联因素的回归系数值.为了评价GTWR结果的有效性, 选择普通最小二乘回归(OLS)与地理加权回归(GWR)对比分析.其中, OLS通过建立全局模型来描述变量间的关系, 而GWR通过参数空间依赖的局部模型对变量间关系的空间非平稳性进行表达, GTWR则能够同时对时间与空间非平稳关系建模.以ArcGIS 10.2为实验平台, 通过载入GTWR_Beta安装包实现GTWR、OLS与GWR模型的运行(http://www.grm.cuhk.edu.hk/~huangbo/GTWR/GTWR_AddIn.rar).不同模型的精度表列入表 1, 可以发现:GTWR的模型AICc的值为45 179.21, 小于OLS的AICc值(53 321.04);GTWR模型的决定系数(R2)以及调整后的决定系数(Radj2)均为0.81, 远大于OLS与GWR对应的值;GTWR、OLS与GWR模型拟合结果的均方根误差(RMSE)分别为10.17、20.29与13.27, 其中, GTWR模型的RMSE最小, 不同的评价指标值均证实GTWR模型效果优于OLS与GWR模型, 即PM2.5与其关联因子间关系存在时空变异特征.此外, 通过多重共线性分析以及统计T检验, 最终识别出6个解释变量, 即:人口规模(千万)、第二产业生产总值(千亿)、SO2排放量(万t)、年平均气温(℃)、年降水量(100 mm)以及年平均相对湿度(%).
|
|
表 1 不同模型的精度评价结果 Table 1 Results of accuracy evaluation of different models |
2.3 治理分区视角下PM2.5浓度关联关系时空变异性分析
以2.1节中识别出的10个联合治理区为基础, 分别对各区域中关联因素的回归系数值进行统计聚合, 得到不同治理区的PM2.5关联因素回归系数值变化曲线.考虑到Ⅷ区(宁甘), Ⅸ区(青藏)与Ⅹ区(新疆)污染程度低, 因此, 本研究重点分析其它治理区中PM2.5关联关系时空变异特征.
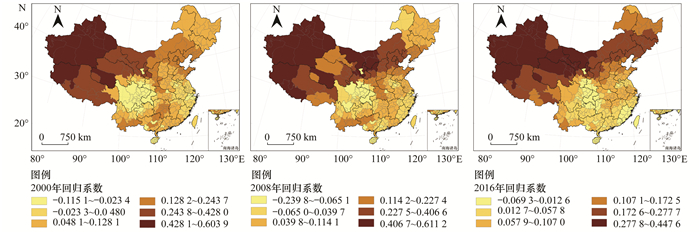
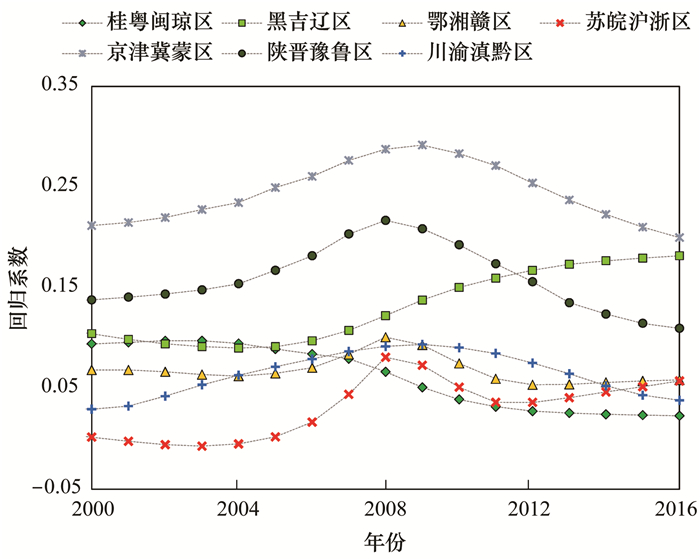
2.3.1 人口因素回归系数值的时空变异特征由GTWR模型分析出的人口因素回归系数值(2000、2008与2016年回归系数值的空间分布如图 4所示)可发现:人口规模对PM2.5浓度的影响主要表现为正向相关, 其中, 影响较高的主要集中于西北与华北地区.各治理区中回归系数值随时间变化的曲线如图 5所示.依据曲线形态的不同, 可将治理区分为三类模式:第一类为“先增后减”型, 回归系数值随时间先增大后减小, 该类包括:Ⅰ区(苏皖沪浙)、Ⅱ区(陕晋豫鲁)、Ⅲ区(鄂湘赣)、Ⅳ区(京津冀蒙)与Ⅶ区(川渝滇黔);第二类为“先减后增”型, 回归系数值总体上随时间先减小后增大, 该类包括:Ⅳ区(黑吉辽);第三类为“单调递减”型, 回归系数值总体上随时间逐渐减小, 该类包括:Ⅴ区(桂粤闽琼).从个体水平上看, Ⅵ区(京津冀蒙)人口因素在2000~2016年对PM2.5浓度的影响程度均是最大的, 平均值约为0.25 μg·(m3·千万人口)-1, 这意味着该区域中城市每增加1千万人口, PM2.5年平均浓度上升约0.25 μg·m-3; 而2000~2008年间人口因素影响程度最小为Ⅰ区(苏皖沪浙), 其回归系数值均接近0 μg·(m3·千万人口)-1, 2009~2016年间人口因素回归系数值最低为Ⅴ区(桂粤闽琼), 约为0.02 μg·(m3·千万人口)-1.
|
图 4 人口因素回归系数空间分布(2000、2008与2016年) Fig. 4 Spatial distribution of population regression coefficient (2000, 2008, and 2016) |
|
图 5 各治理区人口回归系数值变化曲线 Fig. 5 Change curve of population regression coefficient in management areas |
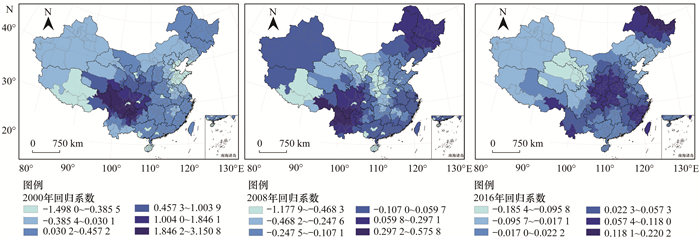
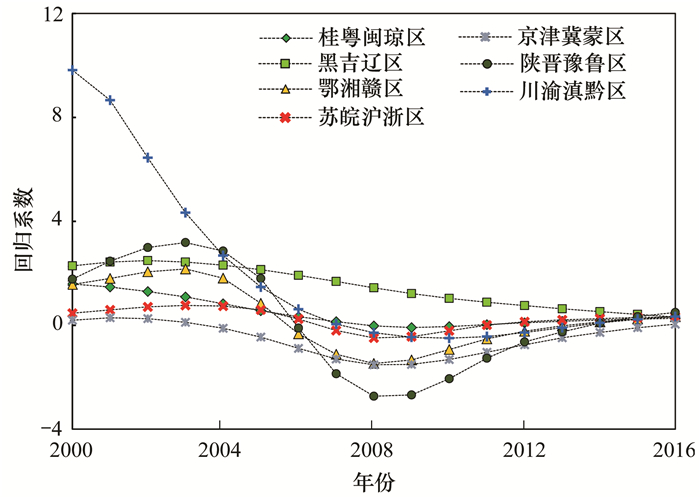
由GTWR所得到第二产业生产总值回归系数值(2000、2008与2016年回归系数值的空间分布如图 6所示)可发现:在整个研究时空范围内, 该因素对PM2.5浓度既有正相关又存在负相关.通过空间统计聚合得到各治理区中第二产业生产总值回归系数值的变化曲线如图 7所示.依据曲线形态的不同, 可以识别出两类模式:第一类为“单调递减”型, 该类包括:Ⅳ区(黑吉辽)、Ⅴ区(桂粤闽琼)与Ⅶ区(川渝滇黔);第二类为“先增再减后增”型, 回归系数值大致上先随时间逐渐增大再减小最后又增大, 该类包括:Ⅰ区(苏皖沪浙)、Ⅱ区(陕晋豫鲁)、Ⅲ区(鄂湘赣)以及Ⅵ区(京津冀蒙).其中, Ⅶ区(川渝滇黔)回归系数值变异程度最大, 由2000年的约10 μg·(m3·千亿元)-1逐渐减小到2008年的0 μg·(m3·千亿元)-1, 随后趋于稳定.
|
图 6 第二产业生产总值回归系数值空间分布(2000、2008与2016年) Fig. 6 Spatial distribution of regression coefficient of total amount of secondary industry (2000, 2008, and 2016) |
|
图 7 各治理区第二产业生产总值回归系数值变化曲线 Fig. 7 Change curve of regression coefficient of total amount of secondary industry in management areas |
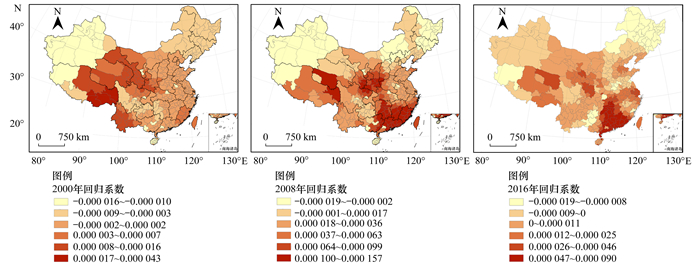
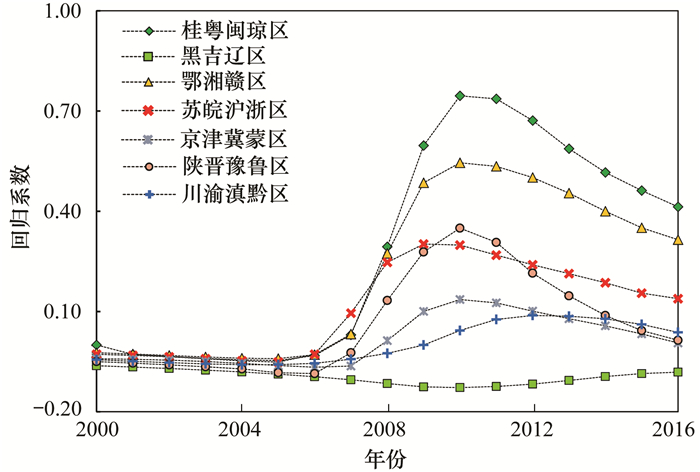
由GTWR所得到SO2排放量回归系数值(2000、2008与2016年回归系数值的空间分布如图 8所示)可发现:在整个研究时空范围中, SO2排放量对PM2.5浓度的影响主要呈正相关关系, 部分负相关的地区主要集中在西北与东北地区.依据图 9中回归系数值变化曲线可知:仅Ⅳ区(黑吉辽)的回归系数值变异程度较小, 呈现“平稳”型变化特征, 其它区域的回归系数值均表现为“先减再增后降”型, 即回归系数值大致上先随时间逐渐减小再增大最后又减小.其中, 2007与2010年左右的回归系数值分别对应的极小值与极大值, 变异程度最大的位于Ⅴ区(桂粤闽琼), 2010年增加到0.70 μg·(m3·万t)-1.
|
图 8 SO2排放量回归系数值空间分布(2000、2008与2016年) Fig. 8 Spatial distribution of regression coefficient of SO2 emissions (2000, 2008, and 2016) |
|
图 9 各治理区SO2排放量回归系数值变化曲线 Fig. 9 Change curve of regression coefficient of SO2 emissions in management areas |
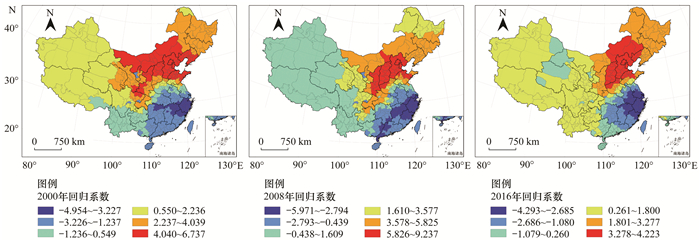
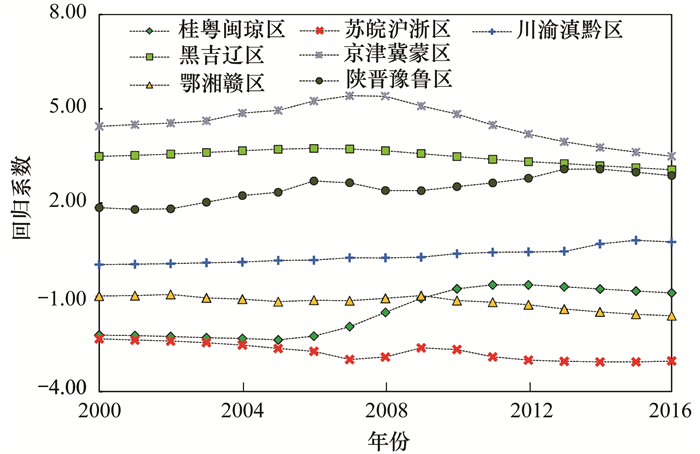
由GTWR所得到年平均温度回归系数值(2000、2008与2016年的回归系数值如图 10所示)可发现:在整个研究时空范围中, 年平均温度对PM2.5浓度的影响既有正向相关亦有负向相关.分区统计的回归系数值变化曲线如图 11所示, Ⅰ区(苏皖沪浙)、Ⅲ区(鄂湘赣)、Ⅳ区(黑吉辽)与Ⅶ区(川渝滇黔)的回归系数值曲线大致上平行于横坐标轴, 时间变异程度较小, 呈现“平稳”型变化特征, 其中, Ⅳ区(黑吉辽)与Ⅶ区(川渝滇黔)的回归系数值均为正, 约为4.5 μg·(m3·℃)-1与0 μg·(m3·℃)-1, 而Ⅰ区(苏皖沪浙)与Ⅲ区(鄂湘赣)的回归系数值为负, 分别为-1.0μg·(m3·℃)-1与-3.5 μg·(m3·℃)-1.此外, Ⅱ区(陕晋豫鲁)与Ⅴ区(桂粤闽琼)的回归系数值分别呈现“单调递增”型与“单调递减”型, Ⅵ区(京津冀蒙)的回归系数值先增大后减小, 各年的回归系数值均是所有区域中最大的值.
|
图 10 年平均温度回归系数值空间分布(2000、2008与2016年) Fig. 10 Spatial distribution of regression coefficient of annual average temperature (2000, 2008, and 2016) |
|
图 11 各治理区年平均温度回归系数值变化曲线 Fig. 11 Change curve of regression coefficient of annual average temperature in management areas |
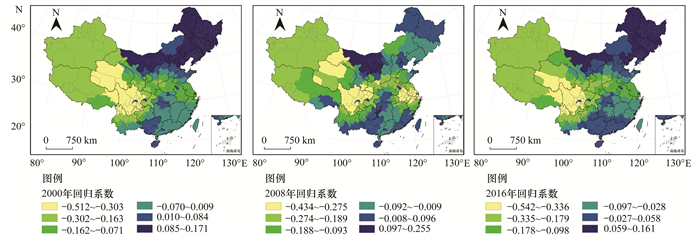
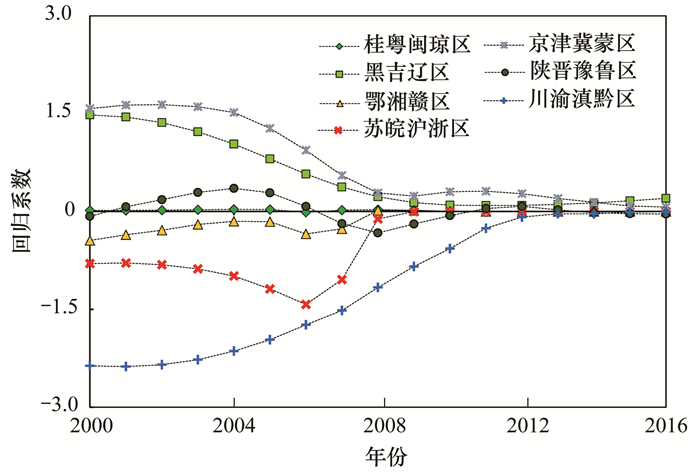
由GTWR所得到年降水量回归系数值(2000、2008与2016年回归系数值空间分布如图 12所示)可发现:在整个研究时空范围内, 年降水量对PM2.5浓度的影响既存在正向相关又有负向相关, 负相关的区域主要位于西北与华东地区.分区统计的回归系数值变化曲线如图 13所示, 依据回归系数值的变化形态的差异, 可以区分四类模式:第一类为“单调递减”型, 该类包括:Ⅳ区(黑吉辽)与Ⅵ区(京津冀蒙), 两者均从2000年的1.5 μg·(m3·100 mm)-1减小到2016年0 μg·(m3·100 mm)-1;第二类为“单调递增”型, 该类包括:Ⅶ区(川渝滇黔), 从2000年的-2.8μg·(m3·100 mm)-1增大到2016年0 μg·(m3·100 mm)-1;第三类为“先减后增”型, 该类包括:Ⅰ区(苏皖沪浙), 2006年的系数值最小, 约为-1.5 μg·(m3·100 mm)-1;第四类为“平稳”型, 包括:Ⅱ区(陕晋豫鲁)、Ⅲ区(鄂湘赣)与Ⅴ区(桂粤闽琼), 回归系数值在0 μg·(m3·100 mm)-1上下波动.
|
图 12 年降水量回归系数值空间分布(2000、2008与2016年) Fig. 12 Spatial distribution of regression coefficient of annual precipitation (2000, 2008, and 2016) |
|
图 13 各治理区年降水量回归系数值变化曲线 Fig. 13 Change curve of regression coefficient of annual precipitation in management areas |
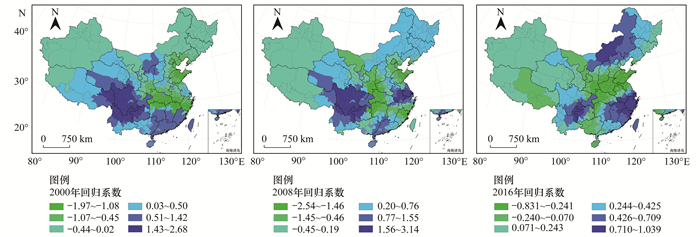
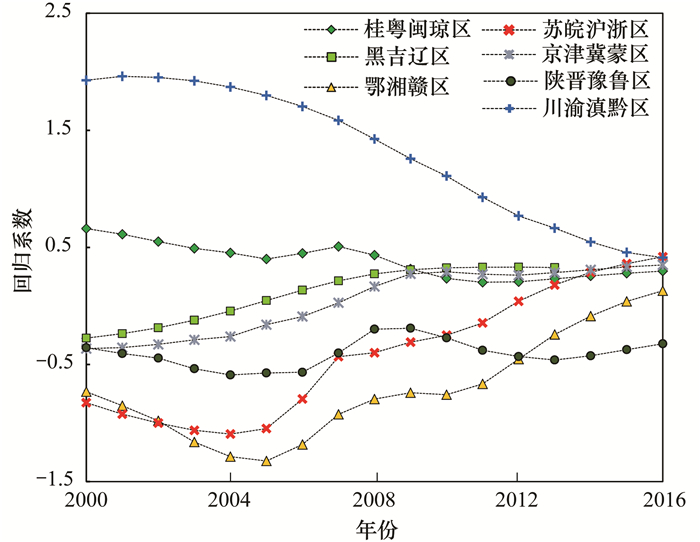
由GTWR所得到年平均相对湿度回归系数值(2000、2008与2016年回归系数值的空间分布如图 14所示)可发现:在整个研究时空范围内, 年平均湿度对PM2.5浓度的影响既有表现正向相关亦有负向相关, 较高的正相关区域主要分布在西南与华东地区, 而较高的负相关区域则主要位于中南地区.治理分区统计的回归系数值变化曲线如图 15所示, 依据形态的差异可识别出三类模式:第一类为“单调递减”型, 该类包括:Ⅴ区(桂粤闽琼)与Ⅶ区(川渝滇黔), 从2000~2016年回归系数值分别减少了0.10与1.5 μg·(m3·%)-1;第二类为“单调递增”型, 该类包括:Ⅳ区(黑吉辽)与Ⅵ区(京津冀蒙), 两者的回归系数值均从2000年的-0.65μg·(m3·%)-1增大到0.4 μg·(m3·%)-1;第三类为“先减后增”型, 该类包括:Ⅰ区(苏皖沪浙)与Ⅲ区(鄂湘赣), 分别在2004年与2005年取极小值-1.0μg·(m3·%)-1与-1.3 μg·(m3·%)-1;第四类为“先减再增后减”型, 该类包括:Ⅱ区(陕晋豫鲁), 在2008年取得最大值, 为-0.25 μg·(m3·%)-1.
|
图 14 年平均相对湿度回归系数值空间分布(2000、2008与2016年) Fig. 14 Spatial distribution of regression coefficient of annual average humidity (2000, 2008, and 2016) |
|
图 15 各治理区年平均相对湿度回归系数值变化曲线 Fig. 15 Change curve of annual average humidity regression coefficient in governance areas |
(1) 以PM2.5为首要污染物, 综合考虑污染程度、地理位置、气象、地形和经济等因素实现了国家尺度上大气污染联合治理区的划分, 该分区结果与存在过污染治理合作的省域较一致, 如:京津冀地区与珠三角地区为包含关系, 长三角地区则完全一致.
(2) 与普通最小二乘回归与地理加权回归相比, 地理时空加权回归能够有效揭示PM2.5与关联因素的时空非平稳关系, 研究证实了人口规模、第二产业生产总值、SO2排放量、年平均气温、年降水量与年平均相对湿度与PM2.5的关系随时空位置发生改变.
(3) 在所识别的联防联控治理单元中, 2000~2016年人口因素对PM2.5浓度主要是正向影响, 其它因素与PM2.5浓度同时存在正向与负向相关, 同时, 由回归系数值在时间维度上变化曲线能够探测出不同因素在各治理区中与PM2.5浓度的关联关系.
| [1] | Liu J, Han Y Q, Tang X, et al. Estimating adult mortality attributable to PM2.5 exposure in China with assimilated PM2.5 Concentrations based on a ground monitoring network[J]. Science of the Total Environment, 2016, 568: 1253-1262. |
| [2] |
曾贤刚, 阮芳芳, 彭彦彦. 基于空间网格尺度的中国PM2.5污染健康效应空间分布[J]. 中国环境科学, 2019, 39(6): 2624-2632. Zeng X G, Ruan F F, Peng Y Y. Health effects' spatial distribution analysis of PM2.5 pollution in China based on spatial grid scale[J]. China Environmental Science, 2019, 39(6): 2624-2632. |
| [3] | Liu M D, Shadbegian R, Zhang B. Does environmental regulation affect labor demand in China? Evidence from the textile printing and dyeing industry[J]. Journal of Environmental Economics and Management, 2017, 86: 277-294. |
| [4] | Luo J Q, Du P J, Samat A, et al. Spatiotemporal pattern of PM2.5 concentrations in mainland China and analysis of its influencing factors using geographically weighted regression[J]. Scientific Reports, 2017, 7: 40607. DOI:10.1038/srep40607 |
| [5] | He Z J, Deng M, Cai J N, et al. Mining spatiotemporal association patterns from complex geographic phenomena[J]. International Journal of Geographical Information Science, 2019. DOI:10.1080/13658816.2019.1566549 |
| [6] |
刘可可, 张红, 刘桂建. 合肥市PM2.5和PM10中元素组成特征及重污染成因分析[J]. 环境科学, 2019, 40(8): 3415-3420. Liu K K, Zhang H, Liu G J. Elemental composition characteristics of PM2.5 and PM10, and heavy pollution analysis in Hefei[J]. Environmental Science, 2019, 40(8): 3415-3420. |
| [7] |
吕喆, 魏巍, 周颖, 等. 2015~2016年北京市3次空气重污染红色预警PM2.5成因分析及效果评估[J]. 环境科学, 2019, 40(1): 1-10. Lv Z, Wei W, Zhou Y, et al. Cause and effect evaluation of PM2.5 during three red alerts in Beijing from 2015 to 2016[J]. Environmental Science, 2019, 40(1): 1-10. |
| [8] |
段杰雄, 翟卫欣, 程承旗, 等. 中国PM2.5污染空间分布的社会经济影响因素分析[J]. 环境科学, 2018, 39(5): 2498-2504. Duan J X, Zhai W X, Cheng C Q, et al. Socio-economic factors influencing the spatial distribution of PM2.5 concentrations in China:an exploratory analysis[J]. Environmental Science, 2018, 39(5): 2498-2504. |
| [9] | Han L J, Zhou W Q, Li W F, et al. Impact of urbanization level on urban air quality:a case of fine particles (PM2.5) in Chinese cities[J]. Environmental Pollution, 2014, 194: 163-170. |
| [10] |
刘海猛, 方创琳, 黄解军, 等. 京津冀城市群大气污染的时空特征与影响因素解析[J]. 地理学报, 2018, 73(1): 177-191. Liu H M, Fang C L, Huang J J, et al. The spatial-temporal characteristics and influencing factors of air pollution in Beijing-Tianjin-Hebei urban agglomeration[J]. Acta Geographica Sinica, 2018, 73(1): 177-191. |
| [11] | Wang Z B, Fang C L. Spatial-temporal characteristics and determinants of PM2.5 in the Bohai rim urban agglomeration[J]. Chemosphere, 2016, 148: 148-162. |
| [12] | Zhou C S, Chen J, Wang S J. Examining the effects of socioeconomic development on fine particulate matter (PM2.5) in China's cities using spatial regression and the geographical detector technique[J]. Science of the Total Environment, 2018, 619-620: 436-445. |
| [13] |
袁凯华, 李后建, 林章悦. 约束性考核促进了官员的减排激励吗[J]. 当代经济科学, 2014, 36(6): 1-10. Yuan K H, Li H J, Lin Z Y. Does constraining assessment enhance the officials' incentives to reduce emission?[J]. Modern Economic Science, 2014, 36(6): 1-10. |
| [14] |
高明, 郭施宏, 夏玲玲. 大气污染府际间合作治理联盟的达成与稳定——基于演化博弈分析[J]. 中国管理科学, 2016, 24(8): 62-70. Gao M, Guo S H, Xia L L. Analysis on the formation and stability of cooperation management alliance of air pollution control among local governments:based on the evolutionary game[J]. Chinese Journal of Management Science, 2016, 24(8): 62-70. |
| [15] |
王金南, 宁淼, 孙亚梅. 区域大气污染联防联控的理论与方法分析[J]. 环境与可持续发展, 2012, 37(5): 5-10. Wang J N, Ning M, Sun Y M. Study on theory and methodology about joint prevention and control of regional air pollution[J]. Environment and Sustainable Development, 2012, 37(5): 5-10. |
| [16] |
汪克亮, 孟祥瑞, 杨宝臣, 等. 技术异质下中国大气污染排放效率的区域差异与影响因素[J]. 中国人口·资源与环境, 2017, 27(1): 101-110. Wang K L, Meng X R, Yang B C, et al. Regional differences and influencing factors of China's air pollution emission efficiency considering technological heterogeneity[J]. China Population, Resources and Environment, 2017, 27(1): 101-110. |
| [17] |
胡志高, 李光勤, 曹建华. 环境规制视角下的区域大气污染联合治理——分区方案设计、协同状态评价及影响因素分析[J]. 中国工业经济, 2019(5): 24-42. Hu Z G, Li G Q, Cao J H. Air pollution regional linkage control and prevention from the perspective of environmental regulation——the scheme design, state evaluation and influencing factors analysis[J]. China Industrial Economics, 2019(5): 24-42. |
| [18] |
刘佳澍, 顾远, 马帅帅, 等. 常州夏冬季PM2.5中无机组分昼夜变化特征与来源解析[J]. 环境科学, 2018, 39(3): 980-989. Liu J S, Gu Y, Ma S S, et al. Day-night differences and source apportionment of inorganic components of PM2.5 during summer-winter in Changzhou city[J]. Environmental Science, 2018, 39(3): 980-989. |
| [19] |
郭文凯, 刘晓, 朱玉凡, 等. 兰州市煨炕污染物排放清单及其对PM2.5浓度贡献[J]. 环境科学, 2018, 39(11): 4849-4857. Guo W K, Liu X, Zhu Y F, et al. Emissions inventory of smoldering Chinese Kangs and their contribution to PM2.5 pollution in Lanzhou city[J]. Environmental Science, 2018, 39(11): 4849-4857. |
| [20] |
尹晓梅, 李梓铭, 熊亚军, 等. 2014~2017北京市气象条件和人为排放变化对空气质量改善的贡献评估[J]. 环境科学, 2019, 40(3): 1011-1023. Yin X M, Li Z M, Xiong Y J, et al. Contribution assessment of meteorology conditions and emission change for air quality improvement in Beijing during 2014-2017[J]. Environmental Science, 2019, 40(3): 1011-1023. |
| [21] |
汪韬阳, 张过, 李沛然, 等. 基于DMSP/OLS夜光遥感影像的城市扩张政策驱动因素分析[J]. 测绘学报, 2018, 47(11): 1466-1473. Wang T Y, Zhang G, Li P R, et al. Analysis on the driving factors of urban expansion policy based on DMSP/OLS remote sensing image[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(11): 1466-1473. |
| [22] | Huang B, Wu B, Barry M. Geographically and temporally weighted regression for modeling spatio-temporal variation in house prices[J]. International Journal of Geographical Information Science, 2010, 24(3): 383-401. |
| [23] | He Q Q, Huang B. Satellite-based mapping of daily high-resolution ground PM2.5 in China via space-time regression modeling[J]. Remote Sensing of Environment, 2018, 206: 72-83. |
| [24] | Chu H J, Huang B, Lin C Y. Modeling the spatio-temporal heterogeneity in the PM10-PM2.5 relationship[J]. Atmospheric Environment, 2015, 102: 176-182. |
| [25] |
杨文涛, 姚诗琪, 邓敏, 等. 北京市PM2.5时空分布特征及其与PM10关系的时空变异特征[J]. 环境科学, 2018, 39(2): 684-690. Yang W T, Yao S Q, Deng M, et al. Spatio-temporal distribution characteristics of PM2.5 and spatio-temporal variation characteristics of the relationship between PM2.5 and PM10 in Beijing[J]. Environmental Science, 2018, 39(2): 684-690. |
| [26] | Shi Y, Ho H C, Xu Y, et al. Improving satellite aerosol optical Depth-PM2.5 correlations using land use regression with microscale geographic predictors in a high-density urban context[J]. Atmospheric Environment, 2018, 190: 23-34. |
 2020, Vol. 41
2020, Vol. 41

