环境科学  2020, Vol. 41 Issue (4): 1513-1519   PDF    
引用本文
刘林钰, 张永军, 李彦胜, 刘欣怡, 万一. 基于深度学习的华东地区PM2.5浓度遥感反演[J]. 环境科学, 2020, 41(4): 1513-1519.
LIU Lin-yu, ZHANG Yong-jun, LI Yan-sheng, LIU Xin-yi, WAN Yi. PM2.5 Inversion Using Remote Sensing Data in Eastern China Based on Deep Learning[J]. Environmental Science, 2020, 41(4): 1513-1519.
基于深度学习的华东地区PM2.5浓度遥感反演
刘林钰, 张永军, 李彦胜, 刘欣怡, 万一     
武汉大学遥感信息工程学院, 武汉 430079
收稿日期: 2019-09-23; 修订日期: 2019-11-14
基金项目: 国家重点研发计划项目（2018YFB0505003）
作者简介: 刘林钰(1995~), 女, 硕士研究生, 主要研究方向为大气遥感, E-mail:linyu_liu@whu.edu.cn
通信作者: 张永军, E-mail:zhangyj@whu.edu.cn
摘要: PM2.5作为大气污染的主要来源，对人类身体健康有着极大的影响.本文提出基于深度学习模型的多要素联合PM2.5反演方法，以PM2.5浓度作为真值数据，引入Himawari气溶胶光学厚度（AOD）日数据产品与温度、相对湿度和气压等10个要素作为反演要素.为验证方法的有效性，采用华东地区2016~2018年的数据分季节开展实验，并与传统反演方法进行对比.结果表明，PM2.5浓度与AOD、降水、风速、高植被覆盖指数呈正相关关系，与矮植被覆盖指数呈负相关关系，与温度、湿度、气压以及DEM的相关性随季节的变化而改变；基于深层神经网络（DNN）反演的PM2.5精度高于传统的线性和非线性模型，各个季节R2均在0.5以上并且误差较小，其中秋季的反演效果最好R2为0.86，夏季为0.75，冬季为0.613，春季为0.566；模型的可视化结果显示，DNN模型的反演结果更接近地面监测站点插值的PM2.5浓度分布，分辨率更高且更精确.
关键词: PM2.5      Himawari数据      华东地区      深度学习      反演     
PM2.5 Inversion Using Remote Sensing Data in Eastern China Based on Deep Learning
LIU Lin-yu , ZHANG Yong-jun , LI Yan-sheng , LIU Xin-yi , WAN Yi     
School of Remote Sensing and Information Engineering, Wuhan University, Wuhan 430079, China
Abstract: PM2.5, which is a major source of air pollution, has a considerable impact on human health. In this study, a multi-element joint PM2.5 inversion method based on a deep learning model is proposed. With PM2.5 concentration as the ground truth, 10 elements including the Himawari-AOD daily data products, temperature, relative humidity, and pressure, were introduced as inversion elements. To verify the effectiveness of the method, the experiment was carried out by season using remote sensing data in Eastern China during 2016-2018. The results demonstrate that PM2.5 concentrations were positively correlated with AOD, precipitation, wind speed, and high vegetation cover index and negatively correlated with dwarf vegetation cover index. The correlation with temperature, humidity, pressure, and DEM changed with seasons. Comparative experiments indicated that the accuracy of PM2.5 inversion based on the deep neural network is higher than that of traditional linear and nonlinear models. R2 was above 0.5, and the error was small in each season. The R2 value for autumn, which showed the best inversion, was 0.86, that for summer was 0.75, that for winter was 0.613, and that for spring was 0.566. The visualization of the model illustrates that the inversion result of the DNN model is closer to the PM2.5 concentration distribution interpolated by the ground monitoring station, and the resolution is higher and more accurate.
Key words: PM2.5      Himawari data      Eastern China      deep learning      inversion     

近年来, 随着我国经济的快速发展, 工业化进程的不断加快, 环境问题日益严重, 霾便是其中之一, 尤其中国华东地区的空气污染日趋严重, 灰霾天气出现频率增多[1, 2].而PM2.5通常指直径小于2.5 μm的颗粒, 是霾的主要成分, 对人体健康和能见度均具有重要影响[3, 4].目前对PM2.5的监测主要以站点的形式开展, 但各个城市国控点的数量有限且分布不均, 难以获取大区域内较为准确的PM2.5浓度信息, 因此使用遥感手段监控大范围内PM2.5浓度具有重要意义[5~7].

AOD为气溶胶光学厚度, 是表征大气浑浊度的重要物理量, 此前有学者研究表明, AOD与PM2.5有较强的相关性[8, 9], Koelemeijer等[10]在研究欧洲气溶胶时加入了边界层高度和相对湿度因子, 提升了PM2.5与AOD的相关性；张智等[11]采用6S模型构建查找表, 以西安为研究区域, 使用MODIS数据中的1 km AOD建立回归模型进行反演；李瑶等[12]利用HJ-1影像, 建立起AOD与PM2.5的线性统计模型.上述反演方法都使用了传统的线性或非线性回归模型, 这一类模型仅适用于短时间且小范围的反演, 精度较低, 无法应对多要素共同反演时的复杂关系.目前国内学者使用深度学习方法反演PM2.5的较少, 大多开展PM2.5的预测研究[13, 14], 申原等[15]提出了基于随机森林的PM2.5反演方法, 直接建立起MODIS影像与PM2.5的关系, 可以取得更好的反演效果.

在此前的反演研究中, 大多都使用MODIS传感器的AOD数据或产品[11, 13, 15], 但该产品每天仅过境2次, 若观测区域在卫星过境时间被云覆盖, 则不能得到有效数据.Himawari-8卫星是日本于2014年10月发射的地球同步卫星, 其搭载的AHI (advanced Himawari imager)传感器有16个波段, 具有更高的时间分辨率, 每10 min就能得到一幅全景影像, 给亚洲及大洋洲区域更详细的气溶胶监测带来了可能[16].目前学者对于Himawari数据的研究, 主要在气溶胶反演、暴雨对流云团监测和冰云识别等方面[17~19], 对PM2.5的反演研究比较匮乏.

综上所述, 传统反演所使用的数据存在如下问题：①时间分辨率低；②覆盖范围小；③数值精度低, 且使用传统模型进行多要素反演效果较差.针对以上问题, 本文使用2016~2018年这3 a的华东地区Himawari AOD数据、ERA5再分析资料和地面高程数据提出一种基于深度学习的PM2.5浓度反演方法并开展实验, 同时与传统的回归模型进行精度对比分析.

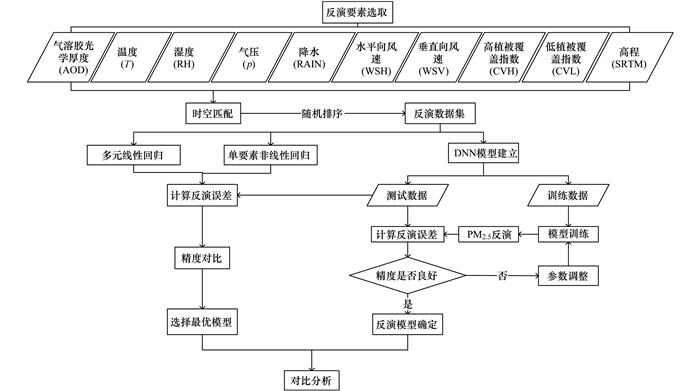
1 材料与方法

本文提出了基于深度学习的多要素联合PM2.5反演方法, 以华东地区459个国控点的PM2.5观测浓度作为真值数据, 以气溶胶光学厚度(Himawari-8 AOD)、温度(T)、相对湿度(RH)、气压(p)、累计降水(RAIN)、水平向风速(WSH)、垂直向风速(WSV)、高植被覆盖指数(CVH)、矮植被覆盖指数(CVL)以及地面数字高程(SRTM)在内的10个要素作为反演要素, 进行华东地区PM2.5反演研究, 具体流程如图 1所示.

图 1 技术流程示意 Fig. 1 Flow chart of the proposed technology

1.1 基于深层神经网络(DNN)的反演模型构建

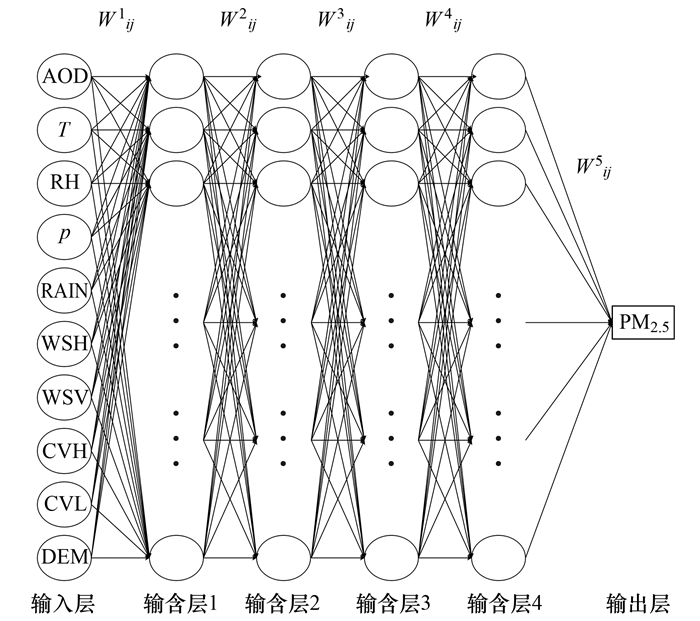
在要素变多的情况下, 各要素之间的关系变得更加复杂, 对模型的非线性拟合能力有了更高要求, 传统线性或非线性回归模型在进行多要素拟合的时候精度都较低, 因此本文使用DNN进行多要素的模型构建.本文构建的深层神经网络结构如图 2所示, 该模型的输入为气溶胶光学厚度、温度和相对湿度等在内的10个反演要素组成的向量, 经过4个隐含层后得到反演结果.每个隐含层均以上一层所有节点的输出作为输入向量, 经激活函数变换后, 逐层向前传递信号.在训练模型时, 采用反向传播损失函数(loss function)的倒数来优化每一层的权重值与偏置值. 本文模型所采用的损失函数为MSE, 其形式为：

图 2 深层神经网络结构 Fig. 2 Deep neural network structure

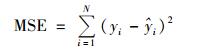
(1)

式中, yi是PM2.5浓度的模型反演值, 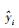为PM2.5浓度的地面真实值, N为样本总个数.

在深度神经网络中, 隐含层里的每一个节点都通过激活函数将输入映射到输出, 常用的激活函数有S型函数(sigmoid)、双曲正切函数(tanh)和线性整流函数(ReLU)等.与深度神经网络在分类中的应用不同, 本模型最终的输出值为一个具体的数值, 而Sigmoid和Tanh等激活函数均将输入信号映射到[0, 1]之间, 与本实验的输出需求不契合；ReLU函数则是一种分段线性函数, 当输入信号大于零的时候其输入等于输出, 当输入信号小于0的时候则输出0, 没有限定输出信号的上限, 同时ReLU函数由于求导简单, 在训练中具备更快的训练速度, 效率更高.故本模型使用ReLU函数作为隐含层神经元的激活函数.

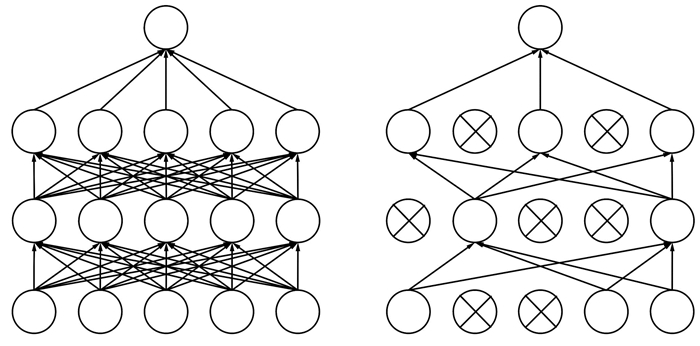
为防止出现过拟合现象, 本文选择在模型中加入随机失活算法(dropout)[20], 即在网络训练过程中按照一定的概率随机将神经元从当前网络中丢弃, 让其不参与到当前训练, 待当前批次训练结束后再将丢弃的神经元恢复并重复上述过程, 如图 3所示.dropout能有效减少神经元之间的共适应关系, 是深度学习中最常用的正则化技术.在本模型中dropout概率设置为0.3.

图 3 随机失活算法示意 Fig. 3 Schematic diagram of the dropout

在模型训练过程中, 优化函数和学习率的设置对模型的训练速度和训练结果有着重要影响.本文选择自适应学习率的优化方式adamx, 它是adam优化函数的一种变体, 不仅具备adam每一次迭代中学习率都有确定范围、参数平稳的优势, 同时令学习率上限范围的界定方法更加简单, 提高了迭代效率[21].在本模型训练过程之中, 初始学习率设为0.001.模型参数设置如表 1所示.

表 1 模型参数设置 Table 1 Model parameter setting

1.2 精度评估

本文采用决定系数(R2)、平均绝对误差(MAD)以及均方根误差(RMSE)作为精度评定标准[22].

决定系数(R2)一般用于回归模型中评估预测值和真实值的符合程度, 一般地, R2越接近1, 表示回归分析中自变量对因变量的解释越好.

平均绝对误差(MAD)是所有单个观测值与算术平均值的偏差的绝对值的平均, 可以避免误差相互抵消的问题, 因而可以准确反映实际预测误差的大小[23].

均方根误差(RMSE)是预测值与真实值偏差的平方与观测次数比值的平方根, 用来衡量预测值与真实值之间的偏差.其值越小, 预测值越接近真实值, 即精度越高.

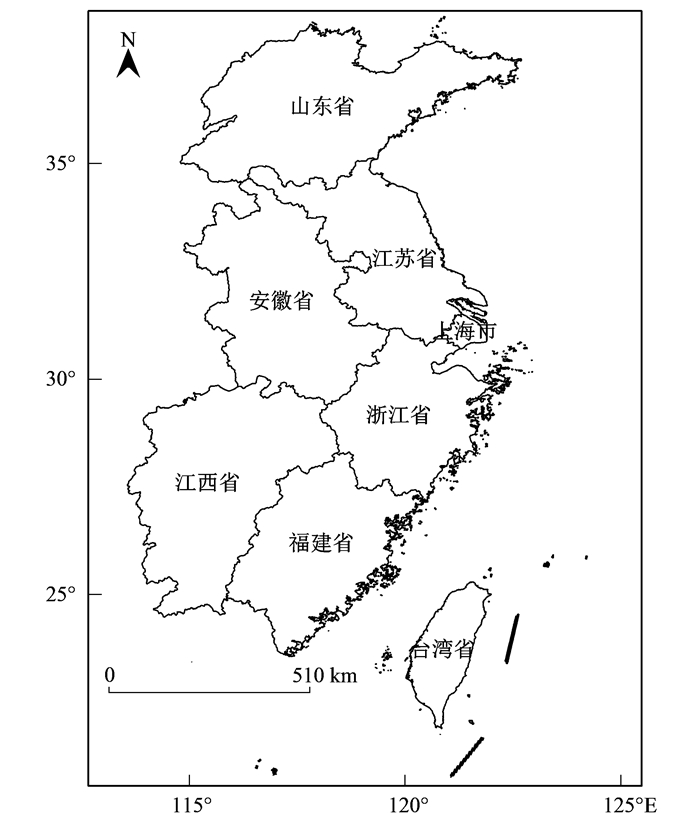
2 结果与讨论 2.1 研究区概况

本文选择的研究区域为中国华东地区, 地理范围为23.56°~38.41°N, 113.57°~122.96°E, 覆盖上海市、浙江省、江苏省、山东省、安徽省、江西省和福建省在内的六省一市, 由于台湾省无国控点, 无法开展实验, 所以本实验未加入对台湾省的分析.本研究区域如图 4所示.

图 4 研究区域示意 Fig. 4 Location of the study area

2.2 实验数据

本实验所用数据见表 2.

表 2 实验数据 Table 2 Experimental dataset

2.3 PM2.5与各反演要素相关性分析

对10个反演要素和地面PM2.5真值进行时空匹配, 共获得66 611条有效数据.对季节进行分割后, 获得春季数据(3~5月)20 290条、夏季数据(6~8月)12 734条、秋季数据(9~11月)16 064条, 冬季数据(12月~次年1、2月)17 523条, 然后使用SPSS软件分析各反演要素与PM2.5的相关性如表 3所示.

表 3 PM2.5与各反演要素间Pearson相关系数 Table 3 Pearson correlation coefficient between PM2.5 and each inversion factor

由表 3得出, PM2.5与气溶胶光学厚度(AOD)的相关性最高, 相关系数均高于0.4, 其中夏季达到了0.542, 因为AOD为表征大气浑浊程度的物理量, 其值越高表明大气污染越强, 相应的PM2.5浓度可能越高；PM2.5与降水(RAIN)、风速(WSH/WSV)呈负相关关系, 降水可以冲刷悬浮于空气中的PM2.5颗粒, 从而降低PM2.5的质量浓度, 风速可以降低PM2.5的积聚, 所以也与PM2.5呈负相关；PM2.5与高植被覆盖指数(CVH)负相关, 矮植被覆盖指数(CVL)正相关, 这与高植被可以更好地吸收、吸附和转移颗粒物有关.而PM2.5与温度(T)、湿度(RH)、气压(p)以及地面数字高程(DEM)的相关性则随季节的变化而改变因而本实验针对4个不同季节分别构建模型.

将4个季节反演数据集的80%用于模型训练, 20%用于验证.为消除数据因时间上连续性带来的偏差, 对数据打乱后随机抽样选取训练数据和验证数据.

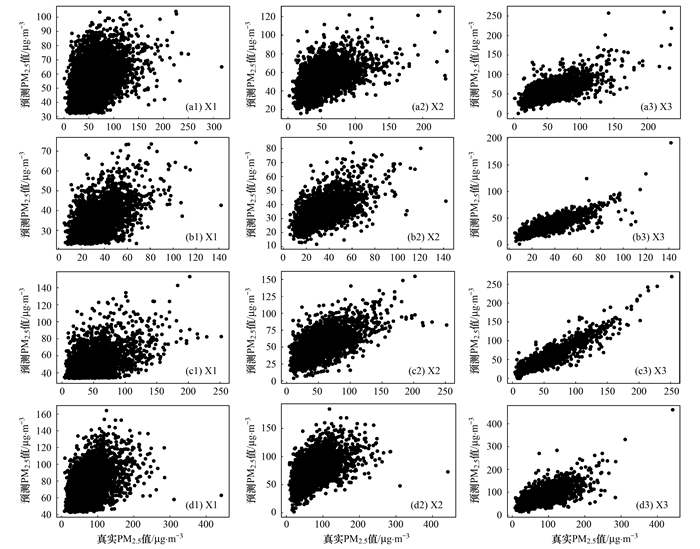
2.4 反演模型结果对比分析 2.4.1 各模型精度评定

按照1.1节所述策略完成基于深层神经网络的反演模型构建(X3模型), 并且与传统的单要素非线性回归[24](X1模型)和多元线性回归模型[25](X2模型)进行对比. 3类反演模型在验证数据集上的反演与效果如图 5所示, 其精度评定结果如表 4所示.

(a)春季; (b)夏季; (c)秋季; (d)冬季 图 5 分季节各反演模型回归效果 Fig. 5 Regression results of the inversion model with seasonal data

表 4 各反演模型精度对比1) Table 4 Comparison of the accuracies of each inversion model

由图 5可见, 与单元素非线性回归(X1)、多元线性回归(X2)结果相比, 在任何季节DNN模型(X3)反演结果的离散程度均更低, 预测值和真实值更接近.

由表 4也可以看出, 无论在任何季节, X1模型精度最低, X2模型加入多种要素反演后的结果更具科学性, 且精度有少量的提升, X3模型在精度上远优于其他两种模型, R2在各个季节均很高(0.5以上), 并且误差相对较小, 可见, 本文提出的基于DNN的反演模型的反演精度优于另外两种模型.同时, 该模型的反演精度与季节有关, 夏季和秋季的反演效果最好, R2分别达到了0.75和0.86, 并且均方根误差为7.64和10.81;春季和冬季的反演效果虽然略逊于夏季和秋季, 但依然整体优于X1和X2方法.

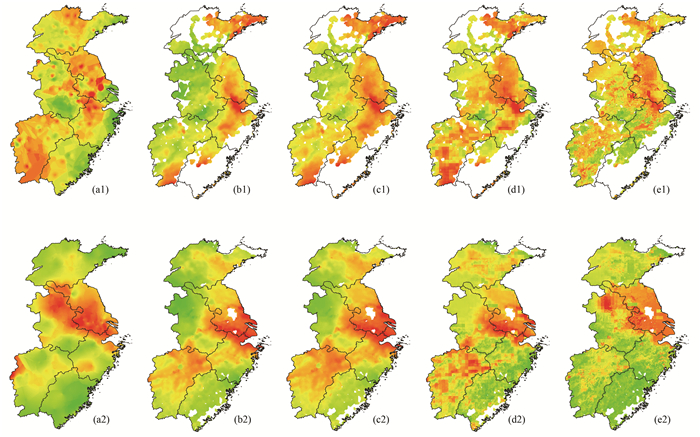
2.4.2 结果可视化分析

对AOD数据进行云量计算, 选择云量覆盖最少的产品进行3种模型的反演并可视化, 结果如图 6所示.

(a1)~(e1)2016-07-25;(a2)~(e2)2017-12-24；(a)国控点PM2.5插值；(b)AOD数据插值；(c)单要素非线性；(d)多元线性；(e)DNN模型 图 6 反演结果对比 Fig. 6 Comparison of inversion results

从2016年7月25日可视化结果可知, 国控点插值出多个PM2.5高值区, 但结果不平滑且分辨率较低.同时, 单要素非线性回归模型与AOD的可视化结果保持较好的一致性, 但并没有反演出安徽中部和江西省的PM2.5高值区；多元线性回归模型的反演效果有所提升, 但粒度偏大；基于DNN的模型不仅与国控点插值结果保持较好的一致性, 并且颗粒度更小、分辨率更高.

从2017年12月24日国测点插值结果可知, 华东地区中部PM2.5浓度最高, 呈中部向南北递减的趋势, 西南部也存在较高的PM2.5.AOD可视化结果在安徽北部并没有较高浓度, 同时单要素非线性回归与多元线性回归模型在安徽北部也呈现低值, 与国控点插值结果相反, 反观基于DNN的反演模型, 其结果与地面监测站点的PM2.5浓度分布更加一致, 并且在地面监测站未有明显PM2.5浓度变化的区域, DNN反演可以得到更小颗粒更精确的结果.

3 结论

(1) PM2.5与反演要素的相关性特征结果表明, 本文选取的10个要素中, PM2.5与AOD、降水、风速、高植被覆盖指数呈正相关关系, 其中对AOD有着较强的正相关性；和矮植被覆盖指数呈负相关关系.而与温度、湿度、气压以及DEM的相关性则随季节的变化而改变.因此, 在不同季节各个要素对PM2.5浓度的变化产生不同的影响, 分季节建模与分析是合理且必要的.

(2) DNN模型为本实验中华东地区PM2.5的最优反演模型：仅使用单要素AOD的反演模型在任何季节的R2都较低, 当加入了其他要素以后R2会有一定程度的提高, 但是多元线性回归模型提升的精度有限, 任何季节的R2都在0.4以下, 而基于DNN的模型反演R2都在0.5以上.并且通过对不同模型可视化的结果分析也可得出, DNN模型的反演效果最好, 分辨率最高.因而本文提出的基于DNN的反演模型可以作为华东地区反演PM2.5的最优模型.

(3) 不同季节的DNN模型效果分析：相比于另外两种反演模型, 基于DNN的反演模型在任何季节都有着较好的反演效果, 但是各个季节之间的效果会存在一定的差异.秋季的反演效果最好R2达到0.86, 夏季次之, 然后是冬季和春季, 虽然不同季节存在差异, 但总体的反演效果都较好.

(4) 华东地区为我国工业水平最高的经济区, 对其快速发展所带来的空气质量问题展开探究, 可以为政府决策提供依据, 也可以为经济的可持续发展提供指导.

参考文献
[1] 郁珍艳, 高大伟, 李正泉, 等. 华东区域PM2.5变化背景下浙江省人口经济暴露水平评估[J]. 环境科学, 2017, 38(12): 4924-4931.
Yu Z Y, Gao D W, Li Z Q, et al. Exposure level of population and economy in Zhejiang Province considering the background of PM2.5 in East China[J]. Environmental Science, 2017, 38(12): 4924-4931.
[2] 郭建平, 吴业荣, 张小曳, 等. BP网络框架下MODIS气溶胶光学厚度产品估算中国东部PM2.5[J]. 环境科学, 2013, 34(3): 817-825.
Guo J P, Wu Y R, Zhang X Y, et al. Estimation of PM2.5 over eastern China from MODIS aerosol optical depth using the back propagation neural network[J]. Environmental Science, 2013, 34(3): 817-825.
[3] 贺晋瑜, 燕丽, 王彦超, 等. 我国PM2.5浓度分阶段改善目标情景分析[J]. 环境科学, 2019, 40(5): 2036-2042.
He J Y, Yan L, Wang Y C, et al. Scenario analysis of PM2.5 concentration targets and milestones in China[J]. Environmental Science, 2019, 40(5): 2036-2042.
[4] 吴健生, 王茜. 基于AOD数据反演地面PM2.5浓度研究进展[J]. 环境科学与技术, 2017, 40(8): 68-76.
Wu J S, Wang X. Research progress of retrieval ground-level PM2.5 concentration based on AOD data[J]. Environmental Science & Technology, 2017, 40(8): 68-76.
[5] 陈辉, 厉青, 李营, 等. 京津冀及周边地区PM2.5时空变化特征遥感监测分析[J]. 环境科学, 2019, 40(1): 33-43.
Chen H, Li Q, Li Y, et al. Monitoring and analysis of the spatio-temporal change characteristics of the PM2.5 concentration over Beijing-Tianjin-Hebei and its surrounding regions based on remote sensing[J]. Environmental Science, 2019, 40(1): 33-43.
[6] 徐建辉, 江洪. 长江三角洲PM2.5质量浓度遥感估算与时空分布特征[J]. 环境科学, 2015, 36(9): 3119-3127.
Xu J H, Jiang H. Estimation of PM2.5 concentration over the Yangtze Delta using remote sensing:analysis of spatial and temporal variations[J]. Environmental Science, 2015, 36(9): 3119-3127.
[7] Li S W, Joseph E, Min Q L. Remote sensing of ground-level PM2.5 combining AOD and backscattering profile[J]. Remote Sensing of Environment, 2016, 183: 120-128. DOI:10.1016/j.rse.2016.05.025
[8] Hoff R M, Christopher S A. Remote sensing of particulate pollution from space:have we reached the promised land?[J]. Journal of the Air & Waste Management Association, 2009, 59(6): 645-675.
[9] 周云云, 张德英, 施润和. 多种气象要素及其变化对AOD与PM2.5关联模型的影响研究[J]. 环境科学学报, 2019, 39(1): 204-211.
Zhou Y Y, Zhang D Y, Shi R H. Influence of multiple meteorological parameters and their variations on the association model of AOD and PM2.5[J]. Acta Scientiae Circumstantiae, 2019, 39(1): 204-211.
[10] Koelemeijer R B A, Homan C D, Matthijsen J. Comparison of spatial and temporal variations of aerosol optical thickness and particulate matter over Europe[J]. Atmospheric Environment, 2006, 40(27): 5304-5315. DOI:10.1016/j.atmosenv.2006.04.044
[11] 张智, 白穆, 游浩妍. 基于MODIS数据的PM2.5反演在大气污染监测中的应用[J]. 测绘科学, 2016, 41(9): 42-46.
Zhang Z, Bai M, You H Y. Application of PM2.5 retrieval in air pollution monitoring with MODIS data[J]. Science of Surveying and Mapping, 2016, 41(9): 42-46.
[12] 李瑶, 刘琳, 胡潭高, 等. 石河子市PM2.5浓度的遥感反演研究[J]. 环境科学与管理, 2018, 43(1): 138-142.
Li Y, Liu L, Hu T G, et al. Remote sensing estimation model of PM2.5 mass concentration in Shihezi City[J]. Environmental Science and Management, 2018, 43(1): 138-142. DOI:10.3969/j.issn.1673-1212.2018.01.031
[13] 黄婕, 张丰, 杜震洪, 等. 基于RNN-CNN集成深度学习模型的PM2.5小时浓度预测[J]. 浙江大学学报(理学版), 2019, 46(3): 370-379.
Huang J, Zhang F, Du Z H, et al. Hourly concentration prediction of PM2.5 based on RNN-CNN ensemble deep learning model[J]. Journal of Zhejiang University (Science Edition), 2019, 46(3): 370-379.
[14] 符海月, 张祎婷. 时间尺度重构EEMD-GRNN改进模型预测PM2.5的研究[J]. 地球信息科学学报, 2019, 21(7): 1132-1142.
Fu H Y, Zhang Y T. Improving the EEMD-GRNN model for PM2.5 prediction based on time scale reconstruction[J]. Journal of Geo-information Science, 2019, 21(7): 1132-1142.
[15] 申原, 陈朝亮, 钱静, 等. 基于随机森林的高分辨率PM2.5遥感反演--以广东省为例[J]. 集成技术, 2018, 7(3): 31-41.
Shen Y, Chen C L, Qian J, et al. High resolution PM2.5 estimation using remote sensing data based on random forest-a case study of Guangdong, China[J]. Journal of Integration Technology, 2018, 7(3): 31-41. DOI:10.3969/j.issn.2095-3135.2018.03.004
[16] Bessho K, Date K, Hayashi M, et al. An introduction to Himawari-8/9-Japan's new-generation geostationary meteorological satellites[J]. Journal of the Meteorological Society of Japan, 2016, 94(2): 151-183. DOI:10.2151/jmsj.2016-009
[17] 葛邦宇, 杨磊库, 陈兴峰, 等. 暗目标法的Himawari-8静止卫星数据气溶胶反演[J]. 遥感学报, 2018, 22(1): 38-50.
Ge B Y, Yang L K, Chen X F, et al. Study on aerosol optical depth retrieval over land from Himawari-8 data based on dark target method[J]. Journal of Remote Sensing, 2018, 22(1): 38-50.
[18] 张夕迪, 孙军. 葵花8号卫星在暴雨对流云团监测中的应用分析[J]. 气象, 2018, 44(10): 1245-1254.
Zhang X D, Sun J. Application analysis of Himawari-8 in monitoring heavy rain convective clouds[J]. Meteorological Monthly, 2018, 44(10): 1245-1254.
[19] 朝鲁门, 宁小莉, 包玉海, 等. 基于葵花-8卫星的白天冰云识别初探[J]. 内蒙古农业大学学报(自然科学版), 2019, 40(2): 45-49.
Chao L M, Ning X L, Bao Y H, et al. Preliminary study of identification day ice cloud based on Himawari-8 data[J]. Journal of Inner Mongolia Agricultural University (Natural Science Edition), 2019, 40(2): 45-49.
[20] Srivastava N, Hinton G, Krizhevsky A, et al. Dropout:a simple way to prevent neural networks from overfitting[J]. Journal of Machine Learning Research, 2014, 15: 1929-1958.
[21] Kingma D P, Ba J. Adam: a method for stochastic optimization[C]. ICLR 2015, 2015. 1-15.
[22] 武紫超.石家庄地区PM2.5浓度的反演模型构建研究[D].石家庄: 河北师范大学, 2019.
Wu Z C. Study on the construction of inversion model of PM2.5 concentration in Shijiazhuang Area[D]. Shijiazhuang: Hebei Normal University, 2019.
[23] 贾俊平, 何晓群, 金勇. 统计学[M]. (第四版). 北京: 中国人民大学出版, 2009: 374.
[24] Bates D M, Watts D G.非线性回归分析及其应用[M].韦博成, 万方焕, 朱宏图, 译.北京: 中国统计出版社, 1997.
[25] 刘严. 多元线性回归的数学模型[J]. 沈阳工程学院学报(自然科学版), 2005, 1(2-3): 128-129.
Liu Y. Mathematical model of multiple linear regression[J]. Journal of Shenyang Institute of Engineering (Natural Science), 2005, 1(2-3): 128-129.