2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
模型是为了特定目的而根据研究对象特有的内在规律, 做出一些必要的简化假设, 运用适当的数学工具得到的原型替代物[1].模型有助于人们理解复杂系统, 并对不同情景模拟下的管理决策进行评估[2].环境模型是研究复杂环境系统的重要工具, 在土地利用、气候变化情景分析、洪水预报、水质管理和环境健康风险评价、污染物在环境中的迁移转化与风险等方面均有应用[3].由于环境模型需要对环境系统进行概念化和抽象化, 进而采用经验性的数学公式或物理方程描述各种环境系统的行为, 往往存在“失真”现象, 经验参数的定义和获取充满不确定性[4, 5].随着对环境系统认识的加深, 环境模型愈趋复杂[6].复杂模型虽然能更好的模拟真实系统过程, 但其所需参数也越来越多, 参数获取困难, 导致参数不确定性增加, 模型输出误差也随之增加.因此, 研究模型输出对输入参数的敏感性极为必要.
在环境模型的构建和应用中引入敏感性分析能够确定敏感参数、帮助数据挖掘和情景设置、降低模型模拟的误差水平, 从而提供更好的辅助决策支持.因此敏感性分析成为了环境模型研究的前沿和热点, 已经成为现代环境模型应用过程中必不可少的环节.
一些学者就某一类型环境模型敏感性分析方法开展了综述研究[7, 8], 其研究侧重于介绍各种敏感性分析方法的数学原理以及在模型中的应用, 而没有阐明敏感性分析方法在模型应用中的具体作用.另一方面, 尽管不同环境模型结构不同, 研究的问题不同, 但其敏感性分析方法是类似的, 也是可以互相借鉴的.因此, 本文对敏感性分析在环境模型应用中的作用进行了总结, 并对常见的敏感性分析方法的原理、应用范围和优缺点进行了综述.最后, 阐述了敏感性分析在环境模型模拟决策中应用的现状和未来研究方向, 以期为研究人员使用某一特定模型时根据敏感性分析的目标选用具体敏感性分析方法提供参考.
1 敏感性分析概述由于研究系统属性的可变性(如不同物种、气象条件、水文条件)及观察与实验室分析的不确定性, 模型参数具有较大的变异性和不确定性.敏感性分析是研究模型参数、初始条件和边界条件等输入的变化对模型输出的影响程度[9].对于仅有少量参数的简单环境模型, 模型输出与各参数呈线性响应关系, 且参数间互不影响, 因此可以快速分析各独立参数对模型输出的影响.而随着模型结构复杂度增加, 模型所需参数和状态变量随之增加.模型输出与模型输入参数间可能存在非线性响应关系或者参数间存在相互作用, 模型输入对模型输出的影响愈加难以定性或量化, 从而敏感性分析难度也随之增加[10].如图 1所示, 随着模型复杂性增加, 模型敏感性亦增加, 在保证各模型输入参数的准确性的前提下模拟结果的准确性也随之增加, 但现实中往往由于各种原因难以保障一些参数的准确性甚至难以获取, 因而, 并非使用越复杂模型越好.
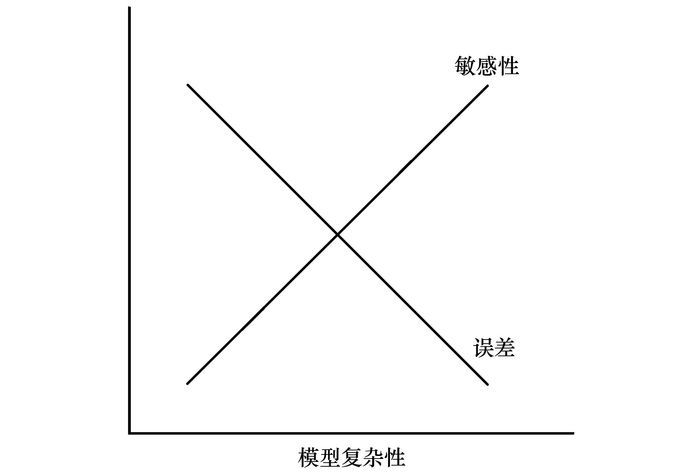
|
图 1 敏感性与模型复杂性关系[10] Fig. 1 Uncertainty-sensitivity relationship model |
敏感性分析是环境模型构建及应用中不可缺少的环节, 应贯穿于模型开发前、开发中以及开发后应用于特定问题的整个过程中[11, 12].敏感性分析的作用通常包括以下7个方面.
(1) 简化模型结构.开展敏感性分析可以识别非敏感参数, 从而将其固定为常量.在一些结构复杂的环境模型中, 由于模型参数众多且在高维空间表现出了复杂的相关性, 可能会出现参数冗余现象.而通过敏感性分析可以识别并移除这些冗余参数[13].
(2) 提高参数率定的效率.通过敏感性分析可以筛选出对模型输出贡献较大的敏感参数, 再对这些敏感参数进行率定, 从而可以减少率定过程的计算量[14, 15].
(3) 分析模型输出不确定性与模型输入参数不确定性的关系, 从而增加模型应用的可靠性[16, 17].
(4) 提高模型的精度.敏感性分析能够筛选出不确定性较大的输入参数, 而这有助于确认数据收集或实验(实地)研究的优先顺序, 进而减少这些输入参数和模型输出的不确定性[18, 19].
(5) 用于确定环境过程中的关键影响因素, 指导环境风险控制措施.
(6) 环境健康风险评价模型中, 敏感性分析可用于确定主要环境污染物, 识别主要暴露途径等关键因子[20].
(7) 环境决策管理模型中, 应用敏感性分析有助于决策者在综合考虑环境效应、经济效益和社会影响等因素下选择合适的决策[21, 22].
2 敏感性分析的数学方法敏感性分析分为局部敏感性分析和全局敏感性分析[23].局部敏感性分析是研究单个输入参数在局部范围内变化时对模型输出响应的影响.最常见的局部敏感性分析方法是一次一个变量法(one-variable-at-a-time approach, OAT)和微分分析法(differential analysis, DA).局部敏感性分析方法简单、计算量小、便于应用, 但其缺点是无法充分描述模型参数的空间分布形态, 并且忽略了参数之间的相互作用[24].而全局敏感性分析研究的是多个模型变量同时变化对模型响应的影响, 从而可以克服局部敏感性分析的缺点.常用的全局敏感性分析方法包括回归分析法、Morris筛选法、Sobol方法、FAST方法和RSA方法等.
2.1 一次一个变量法一次一个变量法(one-variable-at-a-time approach, OAT)的基本原理是分别计算每个参数在其最佳估计值附近进行微小变化(如增减10%)所导致模型输出的变化率, 其变化率的绝对值代表了该参数的敏感性[25].一次一个变量法方法简单、计算量小、便于应用, 适合识别并筛选重要的参数.但其缺点在于:① 目标参数的变化引起的输出结果的灵敏度大小依赖于模型其他参数值的选取, 如果其他参数的基准值存在误差的话, 则分析结果也将存在误差. ② 当模型输出对目标参数呈非线性响应时, 则一次一个变量法无法有效揭示目标参数值变化对模型输出变化的影响. ③ 一次一个变量法也忽略了参数间的相互作用. ④ 无法分析目标参数在更大取值范围的变化如何影响模型输出.
2.2 微分分析法微分分析法(differential analysis, DA)首先将模型进行泰勒展开, 然后根据泰勒展开式计算模型输出对目标参数的一阶偏微分函数值, 则各参数的一阶偏微分函数值代表了该参数的敏感性[26].微分分析法仅在模型局部可微的条件下适用, 偏微分函数的计算难度大, 需要特定的软件.
2.3 回归分析法回归分析法(regression analysis, RA)通过随机采样生成参数样本序列, 计算每个样本对应的模型响应, 然后进行线性回归.建立多元线性模型[27, 28]:
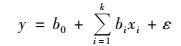
|
式中, y为模型响应, xi为模型参数, k是变量数, ε是误差项, bi为对应于xi的线性回归模型系数, 则可以用标准回归系数、皮尔逊相关系数、斯皮尔曼等级相关系数或偏相关系数等指标表示各参数的敏感性[29, 30].
回归分析法计算相对便捷, 并且可以同时计算多个参数的敏感性.但是敏感性分析结果受回归模型本身的影响, 如果回归模型由于参数变化范围过窄以致于没有产生明显的模型响应, 则分析结果无法揭示真实情况[31].此外, 如果数据间呈现非线性关系或者参数间存在相互作用, 分析结果也将与真实情况存在巨大误差.
2.4 Morris筛选法Morris筛选法由Morris于1991年提出, 随后经Campolongo等进行改进, 是目前应用较广的一种全局敏感性分析方法[32, 33]. Morris筛选法的基本思想是选取模型中某一变量在整个变化范围内进行微小扰动, 其他变量保持不变, 评估该变量微小变化量引起的输出响应变化, 即其提出的基效应概念.记y(x)=y(x1, x2, …, xn), 其中xi为模型某一输入变量, y(x)为运行模型得到的目标函数, n为参数个数, 用di(j)表示第i个参数第j组样本的基效应, 则:
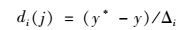
|
式中, y*为参数变化后的输出值; y为参数变化前的输出值; Δi为参数i的变幅; j=1, 2, …, t(t为重复抽样次数).
则可以用di(j)的修正后的均值μi*和标准差σi来判断参数的敏感性:
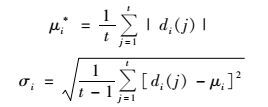
|
式中, μi*表征参数的敏感度, 确定参数的排序, 其值越大, 说明参数的敏感性越强; σi表征参数之间的非线性效应或相互作用的强弱, 其值越高, 参数相互作用越强. Morris筛选法结果可以用散点图表示, μ*为横坐标, σ为纵坐标[17]. Morris筛选法可以简单快速地筛选出敏感性高的参数, 但无法量化这些参数对模型输出变化的影响.值得注意的是, Morris筛选法形式上和一次一个变量法相似, 但鉴于它可以最大化地研究参数空间, 因此仍被视为一种全局敏感性分析方法[34].
2.5 Sobol方法Sobol方法最早由Sobol于1993年提出, 其核心是将模型输出的总方差可分解为每个参数的方差和参数相互作用的方差之和, 然后通过参数对输出方差的贡献比例进行敏感性分级[35].假设模型y=f(xi, x2, …, xn), xi服从[0, 1]均匀分布, 则有:
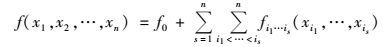
|
Sobol证明了该分解式具有唯一性且每一分解项均可以通过多重积分求得. f(x)总方差为:
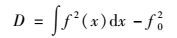
|
偏方差为:
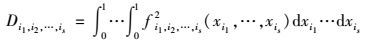
|
其中1≤it<…<is≤n且s=1, 2, …, n.
则敏感度系数Si1, i2, …, is为:
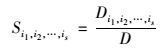
|
式中, Si为xi的一阶敏感度指数, 表示参数单独对模型输出的影响, 也称为主要影响; Si1, i2, …, is叫做因素xi1, xi2, …, xis的s阶敏感性指数, 用于定量描述这s个参数共同作用于f(x).因此对于有s个参数的模型来说, 变量xi1总敏感性指数TSi1可表示为:
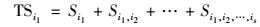
|
Sobol方法不仅可以定性地分析不同模型参数敏感性程度, 也可以定量地分析各参数的敏感性大小.但对于拥有大量参数的复杂环境模型而言, Sobol方法需要消耗巨大的计算资源.此外, Sobol方法没有考虑模型参数间的相关性[36].
2.6 FAST方法FAST(fourier amplitude sensitivity test)理论来源于傅里叶变换(fourier transform)和方差分析方法(analysis of variance, ANOVA). FAST通过计算指定参数造成的模型输出方差在整个模型方差中的贡献, 来衡量参数的一阶敏感性[37~39]. FAST方法采样速度大于Monte Carlo方法, 不受模型结构的影响, 单调、非单调模型均可适用[40].此外, FAST方法对参数的变化范围没有限制, 且优于一些基于相关系数和回归系数的全局敏感性分析方法[41]. FAST方法的缺点在于:① 通常需要大量取样、计算资源消耗量大; ② 忽略参数间的相互作用影响, 无法计算参数的高阶敏感性; ③ 不适合计算离散参数的敏感性[31].耦合FAST和随机平衡设计(random balance design)建立的RBD-FAST方法将所有参数设置成相同的频率, 取样后做随机重组, 模型输出的结果可以根据上一步重组的次序再做傅里叶分解, 从而极大地减少了计算所需要的资源.而由Saltelli等结合Sobol法和FAST的优点提出的EFAST(extended fourier amplitude sensitivity test)可以得到每个参数及参数的相互作用所引起的模型结构的方差, 从而计算参数的高阶敏感性[42].
2.7 RSA方法RSA方法(regional sensitivity analysis)是由Young等于20世纪70年代末、80年代初提的[43, 44].其步骤为:① 按照多元一致分布的原则在可行参数空间内利用蒙特卡罗采样生成参数集; ② 利用生成的参数进行模型模拟, 并按照事先设定的条件, 进行基于行为和非行为的二元划分原则的参数识别; ③ 利用K-S检验或者边缘累积分布函数等方法判断参数对模型的影响程度[45].参数的边缘累积分布离原始分布越远, 则说明该参数对目标函数的影响越显著, 其灵敏度度越高[46]. RSA方法所需假设条件较少无需修改模型, 分析结果直观, 同时还具有参数识别的功能.但是没有考虑参数间相互作用的影响, 无法量化分析参数敏感性.
2.8 各敏感性分析方法综合比较在以上总结的7种敏感性分析方法中, 一次一个变量法(OAT)和微分法(DA)属于局部敏感性分析方法, 回归分析法(RA)、Morris筛选法、Sobol指标法、FAST、RSA属于全局敏感性分析方法(表 1).就计算成本而言, 一次一个变量法最为方便, 微分法数学原理复杂且需要借助于特定软件计算, 计算成本高.回归分析法、Morris筛选法、Sobol指标法、FAST、RSA使用过程中均需要利用蒙特卡罗法或者拉丁超立体采样等方法进行取样进行模拟, 因此对计算资源的占用较大.而这5种方法相互比较, 则回归分析法、Morris筛选法、RSA的计算成本较低, FAST次之、Sobol指标法最高.一次一个变量法以比率或百分比的形式度量敏感性, 直观简单, 但没有考虑参数间的相互作用, 因而适合在参数较少的模型(如经验模型或者半经验模型)中寻找并研究重要参数对模型的影响.回归分析法原理较为简单, 可以用标准回归系数、皮尔逊相关系数、斯皮尔曼等级相关系数或偏相关系数等多种指标衡量参数敏感性.回归分析法适合对参数重要性排名, 寻找重要参数并进行参数校正, 在环境风险评价、水文模型和大气模拟中均有应用. Morris筛选法结果可以用散点图的方式表达, 直观明了. Morris筛选法适合在结构复杂、参数众多的模型(如AGNPS、SWAT等水文模型)中进行初步敏感性分析筛选潜在重要参数进行进一步的分析, 并对非敏感参数进行固定. Sobol指标法和FAST均以参数对模型输出方差的贡献比例衡量敏感性, 适合量化复杂模型中参数的敏感性, 帮助模型选择、数据收集、模型校正和不确定性分析.
|
|
表 1 各敏感性分析方法综合比较 Table 1 Summary of sensitivity analysis methods discussed in this study |
3 敏感性分析在环境模型中的应用
敏感性分析在环境模型中有着广泛的应用, 可概括分析如下.
(1) 用于在环境风险评估中确定主要环境污染物、暴露途径, 以及识别各风险因子对总风险的贡献大小.环境风险评估由于参数数量通常较少, 参数间相互作用的可能性小, 且多为经验或半经验性模型, 因此多应用一次一个变量法和回归分析法等相对简单的敏感性分析方法.如杨彦等[47]进行了电子废弃物拆解场多氯联苯的暴露评估研究, 利用一次一个变量法对暴露源和暴露途径进行鉴定, 发现体重、呼吸速率、实测参数食物摄食、皮肤接触表面积和污染物实测浓度是影响暴露的主要因素. Ligaray等[48]开发了耦合SWAT模型的流域尺度PAHs模型, 对Taehwa流域多环芳烃暴露评估时, 通过一次一个变量法分析识别了主要因素.回归分析法被广泛应用于不同空间尺度上多环芳烃的健康风险评价中, 如Li等[49]开展了上海油条中多环芳烃的终身致癌风险健康风险评价, 并利用多元回归系数分析了不同参数对终身致癌风险模型输出的影响. Wu等[50]则借助于多元回归系数研究识别了全国范围内影响水源水和饮用水多环芳烃健康风险评价的主要参数.
(2) 用于确定环境过程中的关键影响因素, 指导环境风险控制措施. Peng等[51]利用PAM-HMs模型对中国湖南省某地区稻田土壤中Cd污染情况进行了模拟, 同时用一次一个变量法分析并揭示了影响该地区土壤Cd迁移转化及累积的重要参数.在此基础上, 作者进一步总结了该地区土壤修复应关注的易受人为活动影响的重要参数.此外, 一次一个变量法也常用于生命周期评价模型, 通过找到对环境影响较大的阶段和主要环境影响, 并提出相关建议, 以期能够为降低研究对象生命周期过程的资源消耗和环境污染提供参考[52~54]. Bouraoui[55]对PEARL模型应用微分分析法和Morris筛选法进行敏感性分析发现农药降解性能比土壤水力性质具有更重要的影响.
(3) 模型改进优化:帮助模型选择、数据收集、模型校正和不确定性分析.这类应用常见于机制模型, 且由于机制模型结构复杂、参数众多, 因此这类应用中敏感性分析方法多为Morris筛选法、Sobol方法和RSA方法等全局敏感性分析方法.其中, Morris筛选法和Sobol方法被广泛用于众多复杂的水文模型.以SWAT模型为例, 由于模型参数众多, Morris筛选法被用于筛选出重要参数并进行校正[56~58]; 另一方面, SWAT模型由水文子模型、土壤侵蚀子模型和污染负荷子模型构成, 模型结构异常复杂, 当考虑结构化导致的参数相互作用对敏感性分析的影响时, 则可应用Sobol方法开展了敏感性分析.如Zhang等[59]基于Sobol方法的SWAT模型敏感性分析结果有助于理解SWAT的结构、参数校正和不确定性分析.除Morris筛选法和Sobol法外, RSA方法和回归分析法也常用于识别分析模型重要参数. Sun等[60]开发水质模型用于澳大利亚Moruya流域TN、TSS等污染物负荷量模拟研究, 同时用RSA方法分析模型重要参数并进行校正.黄金良等[61]以厦门市小流域, 基于蒙特卡洛随机采样和RSA方法, 从参数的可识别性和灵敏度分析2个方面分析了城市径流模型SWMM模型参数的不确定性.李一平等[62]利用水文模型EFDC(environmental fluid dynamic code)对太湖水动力过程进行了模拟评估, 并利用线性、非线性回归模型识别分析了模型不同输出目标下的重要参数.除了众多全局敏感性分析方法, 一次一个变量法作为局部敏感性分析方法, 由于方法简单, 计算成本低, 在这类应用中也较为常见.例如, 邹宗森等[63]利用以筼筜污水处理厂生物滤池工艺为研究对象, 构建该工艺的BioWin模型, 基于实测数据, 结合一次一个变量法BioWin模型进行校正.席庆等[64]利用农业非点源污染模型AnnAGNPS模型对中田河流域氮磷负荷进行模拟, 采用一次一个变量法分析了多个参数对水文水质结果的敏感性, 分析结果对模型构建中的参数选取与校验调整具有直接参考价值.
(4) 验证模型的可靠性, 洞察模型行为并证明模型结构的稳定性. Yang等[65]将斯皮尔曼秩相关系数用于多环芳烃(PAHs)致癌健康风险评价的参数敏感性分析, 识别鉴定了敏感参数和非敏感参数, 分析结果与前人的研究结果一致, 进一步验证了模型的可靠性.李如忠等[66]等利用OTIS模型解析暂态存储作用对于排水沟渠溶质传输规律的影响, 运用一次一个变量法对模型参数进行敏感性分析, 其研究结果有助于洞察模型行为和证明模型结构的稳定性.张质明等[67]将Sobol方法应用于WASP(The water quality analysis simulation program)模型, 研究表明参数的相互作用对模型输出有着不可忽视的影响, 同时参数间的相关性会影响Sobol敏感性分析结果, 研究结果有助于理解复杂模型的行为.
(5) 研究模拟情景与结果的关系. King等[68]在城市水供给产量研究中, 利用Morris筛选法分析发现影响模型输出的主要参数随着情景改变而变化, 分析结果表明在不同情景下使用重复单一的气候序列估计供水产量将导致错误的模拟结果. Dejonge等[69]利用CERES-Maize模型对农业灌溉管理研究中, 应用Morris筛选法去除非影响参数, 然后应用Sobol方法研究了不同灌溉情景模拟下参数对结果的影响, 为模型在实际场景的应用提供了参考. Ahmed等[70]在基于WMAM模型的城市暴雨低影响开发实践模拟研究中, 利用一次一个变量法分析了不同情景模拟中影响模型的主要参数.
以上研究表明, 对于环境健康风险评价等经验或者半经验环境模型, 由于其参数较少, 参数相互影响小, 所以应用一次一个变量法和回归分析法等原理简单、计算成本低的方法便可得到可靠结果.而对于机制性环境模型, 通常由于这类模型结构复杂、参数众多, 为防止参数相互作用对分析结果的影响, 则多应用全局敏感性分析方法.其中, Morris筛选法和RSA等侧重于定性分析参数敏感性, 虽考虑了参数的相互作用, 却无法量化这种作用, 因此适合快速筛选识别重要参数; Sobol和FAST则可以量化参数间的相互作用, 适合定量分析参数敏感性, 但应用这类敏感性方法时需要考虑方法原理复杂性和计算成本高等因素.总之, 实际研究中需要根据具体的模型和研究目标选择合适的敏感性分析方法.
4 问题与展望(1) 环境模型已广泛应用于环境科学研究中, 而敏感性分析是环境模型应用不可缺少的环节.每种敏感性分析方法均有各自的优缺点, 不存在一种方法明显优于别的方法.局部敏感性分析方法简便、计算成本低, 适用于参数少的经验模型.而对于假设简化较少、结构复杂参数众多的模型, 考虑到难以估量模型输出与模型输入是否存在非线性响应关系, 以及参数间是否存在相互作用, 这种情况下应进行全局敏感性分析.不同全局敏感性分析方法的区别主要在于:① 能否量化模型输入对模型输出的影响; ② 能否计算参数相互作用对模型输出的敏感性; ③ 对计算资源消耗的大小. Morris筛选法和RSA能够定性地分析参数敏感性, 计算成本相对较低, 适合鉴定非敏感参数并将其固定, 同时可以识别潜在敏感参数并用于进一步的定量敏感性分析.回归分析法、Sobol方法和FAST则可以量化各参数或多个参数共同作用对模型输出的影响.
(2) 未来对敏感性分析的研究包括以下4个方面:① 当前常用的全局敏感性分析方法都是基于数理统计原理, 应探寻基于其他原理的敏感性方法. ② 对于占用大量计算资源的全局敏感性分析方法, 寻找更优的算法以提高采样速度, 从而降低计算成本. ③ FAST、Sobol等基于方差的敏感性分析方法忽略了参数间的相关性对分析结果的影响, 这一点也应成为未来研究方向之一. ④ 开发集成各种敏感性分析方法的软件, 以降低模型使用者的门槛. ⑤ 在模型应用中, 应使用多个敏感性分析方法对比分析, 以提高模型结果的稳健性.
| [1] | Giordano F R, Weir M D, Fox W P著. 数学建模[M]. (第五版). 叶其孝, 姜启源, 译. 北京: 机械工业出版社, 2014. |
| [2] | Fitz H C, Kiker G A, Kim J B. Integrated ecological modeling and decision analysis within the everglades landscape[J]. Critical Reviews in Environmental Science and Technology, 2011, 41(S1): 517-547. |
| [3] | Nossent J, Elsen P, Bauwens W. Sobol' sensitivity analysis of a complex environmental model[J]. Environmental Modelling & Software, 2011, 26(12): 1515-1525. |
| [4] | Song X M, Zhan C S, Kong F Z, et al. Advances in the study of uncertainty quantification of large-scale hydrological modeling system[J]. Journal of Geographical Sciences, 2011, 21(5): 801-819. DOI:10.1007/s11442-011-0881-2 |
| [5] | 熊立华, 卫晓婧, 万民. 水文模型两种不确定性研究方法的比较[J]. 武汉大学学报(工学版), 2009, 42(2): 137-142. |
| [6] | 刘毅, 陈吉宁, 杜鹏飞. 环境模型参数优化方法的比较[J]. 环境科学, 2002, 23(2): 1-6. |
| [7] | 田雨, 雷晓辉, 蒋云钟, 等. 水文模型参数敏感性分析方法研究评述[J]. 水文, 2010, 30(4): 9-12, 62. |
| [8] | 宋晓猛, 张建云, 占车生, 等. 水文模型参数敏感性分析方法评述[J]. 水利水电科技进展, 2015, 35(6): 105-112. DOI:10.3880/j.issn.1006-7647.2015.06.020 |
| [9] | Baroni G, Tarantola S. A general probabilistic framework for uncertainty and global sensitivity analysis of deterministic models:a hydrological case study[J]. Environmental Modelling & Software, 2014, 51: 26-34. |
| [10] | Snowling S D, Kramer J R. Evaluating modelling uncertainty for model selection[J]. Ecological Modelling, 2001, 138(1-3): 17-30. DOI:10.1016/S0304-3800(00)00390-2 |
| [11] | Ascough Ⅱ J C, Green T R, Ma L, et al. Key criteria and selection of sensitivity analysis methods applied to natural resource models[EB/OL]. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.134.5105, 2005. |
| [12] | Herman J D, Kollat J B, Reed P M, et al. Technical note:method of morris effectively reduces the computational demands of global sensitivity analysis for distributed watershed models[J]. Hydrology and Earth System Sciences, 2013, 17(7): 2893-2903. DOI:10.5194/hess-17-2893-2013 |
| [13] | Gan Y J, Duan Q Y, Gong W, et al. A comprehensive evaluation of various sensitivity analysis methods:a case study with a hydrological model[J]. Environmental Modelling & Software, 2014, 51: 269-285. |
| [14] | Vanuytrecht E, Raes D, Willems P. Global sensitivity analysis of yield output from the water productivity model[J]. Environmental Modelling & Software, 2014, 51: 323-332. |
| [15] | Zambrano-Bigiarini M, Rojas R. A model-independent particle swarm optimisation software for model calibration[J]. Environmental Modelling & Software, 2013, 43: 5-25. |
| [16] | Makler-Pick V, Gal G, Gorfine M, et al. Sensitivity analysis for complex ecological models-a new approach[J]. Environmental Modelling & Software, 2011, 26(2): 124-134. |
| [17] | Zhan C S, Song X M, Xia J, et al. An efficient integrated approach for global sensitivity analysis of hydrological model parameters[J]. Environmental Modelling & Software, 2013, 41: 39-52. |
| [18] | Fraga I, Charters F J, O'Sullivan A D, et al. A novel modelling framework to prioritize estimation of non-point source pollution parameters for quantifying pollutant origin and discharge in urban catchments[J]. Journal of Environmental Management, 2016, 167: 75-84. DOI:10.1016/j.jenvman.2015.11.003 |
| [19] | Sin G, Gernaey K V, Neumann M B, et al. Global sensitivity analysis in wastewater treatment plant model applications:prioritizing sources of uncertainty[J]. Water Research, 2011, 45(2): 639-651. DOI:10.1016/j.watres.2010.08.025 |
| [20] |
于云江, 向明灯, 孙朋. 健康风险评价中的不确定性[J]. 环境与健康杂志, 2011, 28(9): 835-838. Yu Y J, Xiang M D, Sun P. Uncertainty in health risk assessment:a review of recent related studies[J]. Journal of Environment Health, 2011, 28(9): 835-838. |
| [21] | Song X M, Zhang J Y, Zhan C S, et al. Global sensitivity analysis in hydrological modeling:review of concepts, methods, theoretical framework, and applications[J]. Journal of Hydrology, 2015, 523: 739-757. DOI:10.1016/j.jhydrol.2015.02.013 |
| [22] | Anderson B, Borgonovo E, Galeotti M, et al. Uncertainty in climate change modeling:can global sensitivity analysis be of help?[J]. Risk Analysis, 2014, 34(2): 271-293. DOI:10.1111/risa.2014.34.issue-2 |
| [23] | Mousivand A, Menenti M, Gorte B, et al. Global sensitivity analysis of the spectral radiance of a soil-vegetation system[J]. Remote Sensing of Environment, 2014, 145: 131-144. DOI:10.1016/j.rse.2014.01.023 |
| [24] | Wainwright H M, Finsterle S, Zhou Q L, et al. Modeling the performance of large-scale CO2 storage systems:a comparison of different sensitivity analysis methods[J]. International Journal of Greenhouse Gas Control, 2013, 17: 189-205. DOI:10.1016/j.ijggc.2013.05.007 |
| [25] | Cho E, Arhonditsis G B, Khim J, et al. Modeling metal-sediment interaction processes:parameter sensitivity assessment and uncertainty analysis[J]. Environmental Modelling & Software, 2016, 80: 159-174. |
| [26] | Helton J C, Davis F J. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems[J]. Reliability Engineering & System Safety, 2003, 81(1): 23-69. |
| [27] | Olaya-Abril A, Parras-Alcántara L, Lozano-García B, et al. Soil organic carbon distribution in mediterranean areas under a climate change scenario via multiple linear regression analysis[J]. Science of the Total Environment, 2017, 592: 134-143. DOI:10.1016/j.scitotenv.2017.03.021 |
| [28] |
程晓光, 张静, 宫辉力. 半干旱半湿润地区HSPF模型水文模拟及参数不确定性研究[J]. 环境科学学报, 2014, 34(12): 3179-3187. Cheng X G, Zhang J, Gong H L. HSPF hydrologic simulation and parameter uncertainty in a semi-arid and semi-humid area[J]. Acta Scientiae Circumstantiae, 2014, 34(12): 3179-3187. |
| [29] | Montgomery D C, Peck E A, Vining G G. Introduction to linear regression analysis[M]. New York:John Wiley & Sons, 2015. |
| [30] | Cohen J, Cohen P, West S G, et al. Applied multiple regression/correlation analysis for the behavioral sciences[M]. Mahwah, NJ:Routledge, 2013. |
| [31] | Christopher Frey H, Patil S R. Identification and review of sensitivity analysis methods[J]. Risk Analysis, 2002, 22(3): 553-578. DOI:10.1111/risk.2002.22.issue-3 |
| [32] | Gamerith V, Neumann M B, Muschalla D. Applying global sensitivity analysis to the modelling of flow and water quality in sewers[J]. Water Research, 2013, 47(13): 4600-4611. DOI:10.1016/j.watres.2013.04.054 |
| [33] | Yi X, Zou R, Guo H C. Global sensitivity analysis of a three-dimensional nutrients-algae dynamic model for a large shallow lake[J]. Ecological Modelling, 2016, 327: 74-84. DOI:10.1016/j.ecolmodel.2016.01.005 |
| [34] | Neumann M B. Comparison of sensitivity analysis methods for pollutant degradation modelling:a case study from drinking water treatment[J]. Science of the Total Environment, 2012, 433: 530-537. DOI:10.1016/j.scitotenv.2012.06.026 |
| [35] | Bilotta G, Cappello A, Hérault A, et al. Sensitivity analysis of the MAGFLOW cellular automaton model for lava flow simulation[J]. Environmental Modelling & Software, 2012, 35: 122-131. |
| [36] | Wan H, Xia J, Zhang L P, et al. Sensitivity and interaction analysis based on Sobol' method and its application in a distributed flood forecasting model[J]. Water, 2015, 7(6): 2924-2951. DOI:10.3390/w7062924 |
| [37] | Wang J, Li X, Lu L, et al. Parameter sensitivity analysis of crop growth models based on the extended fourier amplitude sensitivity test method[J]. Environmental Modelling & Software, 2013, 48: 171-182. |
| [38] | Cukier R I, Levine H B, Shuler K E. Nonlinear sensitivity analysis of multiparameter model systems[J]. Journal of Computational Physics, 1978, 26(1): 1-42. DOI:10.1016/0021-9991(78)90097-9 |
| [39] | Guse B, Reusser D E, Fohrer N. How to improve the representation of hydrological processes in SWAT for a lowland catchment-temporal analysis of parameter sensitivity and model performance[J]. Hydrological Processes, 2014, 28(4): 2651-2670. DOI:10.1002/hyp.9777 |
| [40] | Bui D T, Tuan T A, Hoang N D, et al. Spatial prediction of rainfall-induced landslides for the Lao Cai area (Vietnam) using a hybrid intelligent approach of least squares support vector machines inference model and artificial bee colony optimization[J]. Landslides, 2017, 14(2): 447-458. DOI:10.1007/s10346-016-0711-9 |
| [41] | Saltelli A, Bolado R. An alternative way to compute fourier amplitude sensitivity test (FAST)[J]. Computational Statistics & Data Analysis, 1998, 26(4): 445-460. |
| [42] | Luan W F, Lu L, Li X, et al. Weight determination of sustainable development indicators using a global sensitivity analysis method[J]. Sustainability, 2017, 9(2): 303. DOI:10.3390/su9020303 |
| [43] | Young P C. General theory of modelling for badly defined dynamic systems[A]. In:Vansteenkiste G C (Ed.). Modeling, Identification and Control in Environmental Systems GC Vansteenkiste[M]. Amsterdam:North-Holland, 1978. |
| [44] | Norton J. An introduction to sensitivity assessment of simulation models[J]. Environmental Modelling & Software, 2015, 69: 166-174. |
| [45] | Pianosi F, Wagener T. A simple and efficient method for global sensitivity analysis based on cumulative distribution functions[J]. Environmental Modelling & Software, 2015, 67: 1-11. |
| [46] | 邓义祥, 王琦, 赖斯芸, 等. 优化、RSA和GLUE方法在非线性环境模型参数识别中的比较[J]. 环境科学, 2003, 24(6): 9-15. |
| [47] |
杨彦, 于云江, 李定龙, 等. 电子废弃物拆解场多氯联苯含量及健康风险评价[J]. 中国环境科学, 2012, 32(4): 727-735. Yang Y, Yu Y J, Li D L, et al. Concentration and health risk assessment of PCBs in E-waste dismantling field[J]. China Environmental Science, 2012, 32(4): 727-735. |
| [48] | Ligaray M, Baek S S, Kwon H O, et al. Watershed-scale modeling on the fate and transport of polycyclic aromatic hydrocarbons (PAHs)[J]. Journal of Hazardous Materials, 2016, 320: 442-457. DOI:10.1016/j.jhazmat.2016.08.063 |
| [49] | Li G, Wu S M, Wang L, et al. Concentration, dietary exposure and health risk estimation of polycyclic aromatic hydrocarbons (PAHs) in Youtiao, a Chinese traditional fried food[J]. Food Control, 2016, 59: 328-336. DOI:10.1016/j.foodcont.2015.06.003 |
| [50] | Wu B, Zhang Y, Zhang X X, et al. Health risk assessment of polycyclic aromatic hydrocarbons in the source water and drinking water of China:quantitative analysis based on published monitoring data[J]. Science of the Total Environment, 2011, 410-411: 112-118. DOI:10.1016/j.scitotenv.2011.09.046 |
| [51] | Peng C, Wang M E, Chen W P. Modelling cadmium contamination in paddy soils under long-term remediation measures:model development and stochastic simulations[J]. Environmental Pollution, 2016, 216: 146-155. DOI:10.1016/j.envpol.2016.05.038 |
| [52] |
刘凯辉, 徐建全. 纯电动汽车驱动电机全生命周期评价[J]. 环境科学学报, 2016, 36(9): 3456-3463. Liu K H, Xu J Q. Life cycle assessment of driving motor on electric vehicle[J]. Acta Scientiae Circumstantiae, 2016, 36(9): 3456-3463. |
| [53] |
杨东, 刘晶茹, 杨建新, 等. 基于生命周期评价的风力发电机碳足迹分析[J]. 环境科学学报, 2015, 35(3): 927-934. Yang D, Liu J R, Yang J X, et al. Carbon footprint of wind turbine by life cycle assessment[J]. Acta Scientiae Circumstantiae, 2015, 35(3): 927-934. |
| [54] |
孙锌, 刘晶茹, 杨东, 等. 家用空调碳足迹及其关键影响因素分析[J]. 环境科学学报, 2014, 34(4): 1054-1060. Sun X, Liu J R, Yang D, et al. The carbon footprint of household air-conditioner and its key influence factors[J]. Acta Scientiae Circumstantiae, 2014, 34(4): 1054-1060. |
| [55] | Bouraoui F. Testing the PEARL model in the Netherlands and Sweden[J]. Environmental Modelling & Software, 2007, 22(7): 937-950. |
| [56] | Licciardello F, Toscano A, Cirelli G L, et al. Evaluation of sediment deposition in a mediterranean reservoir:comparison of long term bathymetric measurements and SWAT estimations[J]. Land Degradation & Development, 2017, 28(2): 566-578. |
| [57] | Ahmadi M, Ascough Ⅱ J C, Dejonge K C, et al. Multisite-multivariable sensitivity analysis of distributed watershed models:enhancing the perceptions from computationally frugal methods[J]. Ecological Modelling, 2014, 279: 54-67. DOI:10.1016/j.ecolmodel.2014.02.013 |
| [58] | Sarrazin F, Pianosi F, Wagener T. Global sensitivity analysis of environmental models:convergence and validation[J]. Environmental Modelling & Software, 2016, 79: 135-152. |
| [59] | Zhang C, Chu J G, Fu G T. Sobol's sensitivity analysis for a distributed hydrological model of Yichun river basin, China[J]. Journal of Hydrology, 2013, 480: 58-68. DOI:10.1016/j.jhydrol.2012.12.005 |
| [60] | Sun X Y, Newham L T, Croke B F W, et al. Three complementary methods for sensitivity analysis of a water quality model[J]. Environmental Modelling & Software, 2012, 37: 19-29. |
| [61] |
黄金良, 林杰, 杜鹏飞. 城市降雨径流模拟的参数不确定性分析[J]. 环境科学, 2012, 33(7): 2224-2234. Huang J L, Lin J, Du P F. Parameter uncertainty analysis for urban rainfall runoff modelling[J]. Environmental Science, 2012, 33(7): 2224-2234. |
| [62] |
李一平, 邱利, 唐春燕, 等. 湖泊水动力模型外部输入条件不确定性和敏感性分析[J]. 中国环境科学, 2014, 34(2): 410-416. Li Y P, Qiu L, Tang C Y, et al. Uncertainty and sensitivity analysis of input conditions in large shallow lake hydrodynamic model[J]. China Environmental Science, 2014, 34(2): 410-416. |
| [63] |
邹宗森, 施汉昌, 陈向强, 等. 生物滤池工艺的数值模拟与运行优化[J]. 环境科学, 2014, 35(12): 4627-4635. Zou Z S, Shi H C, Chen X Q, et al. Numerical simulation and operation optimization of biological filter[J]. Environmental Science, 2014, 35(12): 4627-4635. |
| [64] |
席庆, 李兆富, 罗川. 基于扰动分析方法的AnnAGNPS模型水文水质参数敏感性分析[J]. 环境科学, 2014, 35(5): 1773-1780. Xi Q, Li Z F, Luo C. Sensitivity analysis of AnnAGNPS model's hydrology and water quality parameters based on the perturbation analysis method[J]. Environmental Science, 2014, 35(5): 1773-1780. |
| [65] | Yang W, Lang Y G, Li G L. Cancer risk of polycyclic aromatic hydrocarbons (PAHs) in the soils from Jiaozhou Bay wetland[J]. Chemosphere, 2014, 112: 289-295. DOI:10.1016/j.chemosphere.2014.04.074 |
| [66] |
李如忠, 钱靖, 董玉红, 等. 城郊排水沟渠溶质传输的暂态存储影响及参数灵敏性[J]. 环境科学, 2015, 36(2): 481-489. Li R Z, Qian J, Dong Y H, et al. Influence of transient storage on solute transport and the parameter sensitivity analysis in a suburban drainage ditch[J]. Environmental Science, 2015, 36(2): 481-489. |
| [67] |
张质明, 王晓燕, 李明涛, 等. 基于全局敏感性分析方法的WASP模型不确定性分析[J]. 中国环境科学, 2014, 34(5): 1336-1346. Zhang Z M, Wang X Y, Li M T, et al. Uncertainty analysis of WASP based on global sensitivity analysis method[J]. China Environmental Science, 2014, 34(5): 1336-1346. |
| [68] | King D M, Perera B J C. Morris method of sensitivity analysis applied to assess the importance of input variables on urban water supply yield-a case study[J]. Journal of Hydrology, 2013, 477: 17-32. DOI:10.1016/j.jhydrol.2012.10.017 |
| [69] | Dejonge K C, Ascough J C, Ahmadi M, et al. Global sensitivity and uncertainty analysis of a dynamic agroecosystem model under different irrigation treatments[J]. Ecological Modelling, 2012, 231: 113-125. DOI:10.1016/j.ecolmodel.2012.01.024 |
| [70] | Ahmed K, Chung E S, Song J Y, et al. Effective design and planning specification of low impact development practices using water management analysis module (WMAM):case of Malaysia[J]. Water, 2017, 9(3): 173. DOI:10.3390/w9030173 |
 2017, Vol. 38
2017, Vol. 38

