2. 北京大学城市与环境学院, 地表过程分析与模拟教育部重点实验室, 北京 100871;
3. 深圳市城市规划设计研究院, 城市发展与土地政策研究所, 深圳 518055
2. Laboratory of Earth Surface Processes of Ministry of Education, College of Urban and Environment Science, Peking University, Beijing 100871, China;
3. Department of Urban Development and Land Policy, Urban Planning and Design Institute of Shenzhen, Shenzhen 518055, China
随着城市化进程的加快, 城市面积、人口持续扩张, 工业排放、能源消耗和机动车持有量不断增加, 我国主要城市空气质量指数暴表事件频发, 大气污染成为了社会各界讨论的热点问题.目前, 我国的细颗粒物污染呈现逐年增加的趋势, 尤其是在中东部地区[1], 26%的区域[2]PM2.5浓度超过了国家规定(GB 3095-2012) 的日均PM2.5浓度限值35 μg·m-3, 高于世界卫生组织指导值(AQGs)的3.5倍以上.大气污染, 尤其是细颗粒物污染, 已成为制约京津冀地区乃至我国可持续发展的关键环境问题, 也是世界上许多大城市在城镇化进程中普遍面临的一个难题[3].
细颗粒物又称PM2.5, 是指环境空气中空气动力学当量直径小于等于2.5 μm的颗粒物. PM2.5已成为我国大气复合污染的首要污染物[4]. PM2.5污染作为一种时空上连续且不均匀分布的现象, 其时空浓度的分异受到如气候[5, 6]、地形[7, 8]和人类活动[9, 10]等不同因素的影响, 明确其浓度的空间分布特征对于大气污染防治和流行病学的研究均有重要的意义.从2012年12月起, 我国在京津冀、长三角、珠三角区域及直辖市、省会城市和计划单列市等74个城市建立了PM2.5监测网络, 并开始实时向公众发布PM2.5监测数据.但是由于监测站的建设成本高昂, 一个城市的站点有限, 并不能完全覆盖整个城市, 更不能用一个笼统的数据来概括整个城市的空气质量状况.此外, 我国的很多流行病学研究多采用研究区内PM2.5浓度的均值[11~13], 或者采用简单的空间插值方法[14, 15]得到的PM2.5浓度的空间分布作为剂量反应函数的自变量, 这些方法通常不能真实反映研究区内的PM2.5浓度的空间分异.而土地利用回归模型有着很强的模拟污染物浓度的空间分异的能力, 并且将覆盖范围广的卫星遥感数据产品大气气溶胶光学厚度AOD(aerosol optical depth)用于地面PM2.5浓度的模拟[16, 17], 恰到好处地弥补了以上缺陷. AOD数据产品多种多样, 常见的是MODIS(moderate resolution imaging spectroradiometer)的AOD数据.近年来, Suomi NPP卫星搭载的VIIRS(visible infrared imaging radiometer, 可见光红外辐射计组合仪)所提供的气溶胶产品成为了PM2.5遥感反演的热点[18], VIIRS AOD较MODIS AOD有空间覆盖度广、空间分辨率高、条带间无间隔等优势, 在模拟地面空气质量方面有较大的应用前景[19, 20].
本研究利用有限的站点监测数据, 结合VIIRS AOD、土地覆被、气象因子、道路分布、人口密度、污染源分布等信息, 分别利用最小二乘和地理加权回归的土地利用回归模型对PM2.5浓度时空分布情况进行模拟, 比较两种方法对京津冀地区PM2.5浓度在不同时段的空间模拟结果, 并分析不同回归模型的特点.
1 材料与方法环境保护部发布的报告[21]指出, 京津冀地区是我国空气污染最严重的区域, 首要污染物为细颗粒物, 其年均浓度为93 μg·m-3.京津冀地区13个地级以上城市中, 有12城市细颗粒物浓度超标, 有11个城市排在污染最重的前20位, 其中有8个城市排在前10位, 区域内PM2.5年均浓度平均超标1.6倍以上, 空气重度及以上污染天数占全年天数17%.
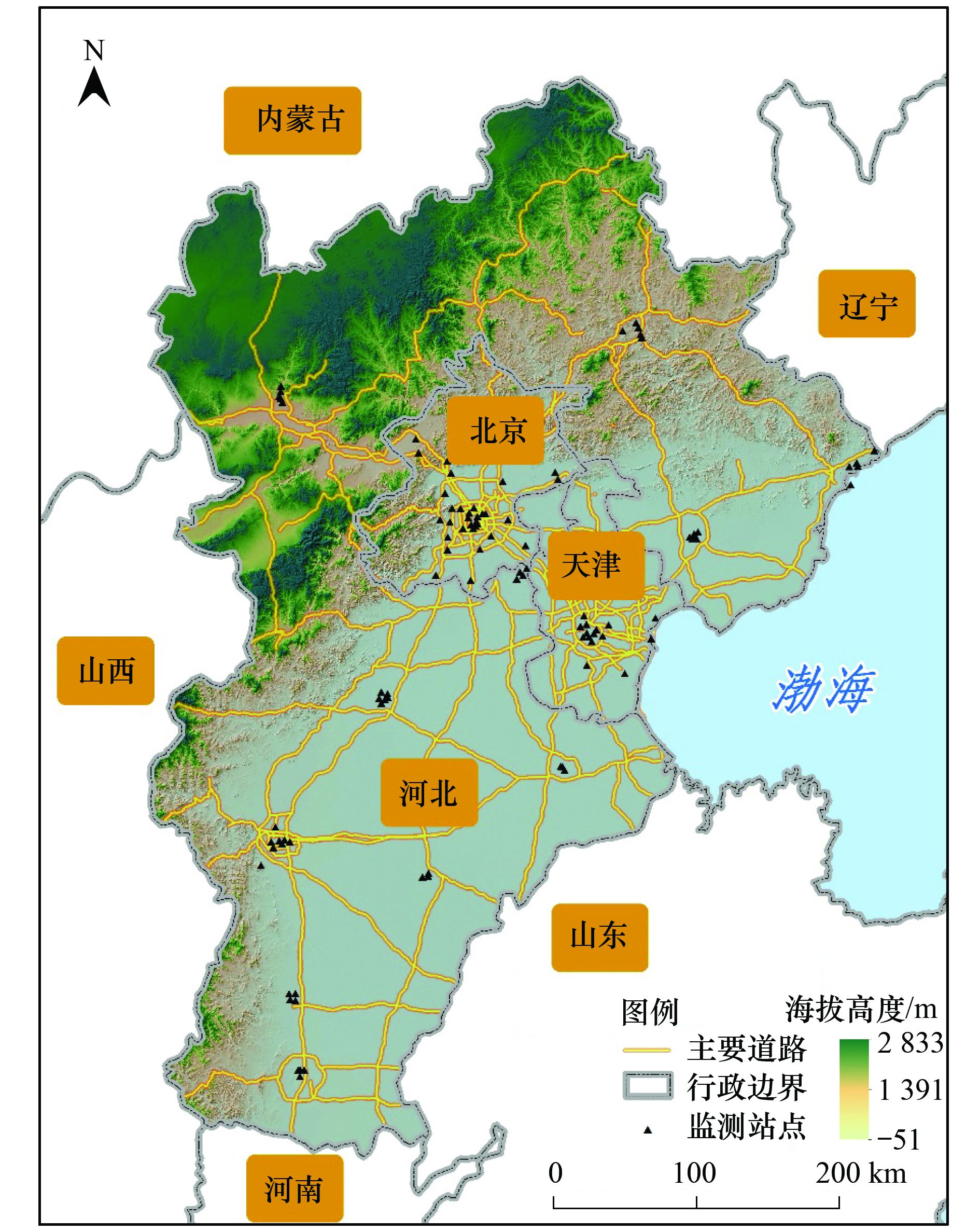
1.1 数据来源及预处理研究所用的资料主要有由中国环境监测总站(http://113.108.142.147:20035/emcpublish/)和北京市环境保护监测中心(http://zx.bjmemc.com.cn/)提供的2014年1月1日至2014年12月31日的PM2.5小时监测数据.京津冀地区共有104个监测站点, 其中北京市有36个站点, 天津市有15个站点, 河北省有53个站点.各站点的空间分布情况如图 1所示.
|
图 1 京津冀地区空气质量监测站点分布情况示意 Fig. 1 Distribution of air quality monitoring sites in Beijing-Tianjin-Hebei region |
本研究用到的资料还有来源于美国国家海洋和大气管理局(NOAA)卫星应用和研究中心(STAR)官方网站(http://www.star.nesdis.noaa.gov/smcd/emb/viirs_aerosol/index.php)提供的VIIRS Aerosol Environmental Data Record (EDR) AOD数据产品.省、地、市行政边界数据来源于国家基础地理信息系统网站(http://nfgis.nsdi.gov.cn).土地覆被数据(2010) 来源于国家基础地理信息中心GlobeLand30网站(http://www.globeland30.org/GLC30Download/index.aspx), 空间分辨率为30m.京津冀地区气象数据(2014) 来源于中国气象科学数据共享服务网(http://cdc.nmic.cn/home.do), 该数据集提供了京津冀地区26个气象站点的日值气象数据, 包括平均气温(℃)、平均风速(m·s-1)、平均相对湿度(%)、最大风速的风向(16个方位)、日降水量(mm).路网数据由矢量化OpenStreetMap Data Extracts (http://download.geofabrik.de/)的数据得到, 分为主干道和次要道路两类.归一化植被指数(NDVI)数据为MODIS MOD13Q1数据集, 来源于美国国家航空航天局戈达德宇宙飞行中心(NASA Goddard Space Flight Center)网站(https://ladsweb.nascom.nasa.gov/data/search.html), 具有250 m的空间分辨率, 每隔16 d提供一次.所用到的数字高程数据(DEM)为ASTER GDEM V2全球数字高程数据, 来源于地理空间数据云(http://www.gscloud.cn/), 空间分辨率为30 m.废气排放重点污染源数据来源于环境保护部发布的2014年国家重点监控企业名单(http://www.zhb.gov.cn/gkml/hbb/bgt/201312/t20131231_265877.htm), 污染源分布情况借助于公众环境研究中心(IPE)公布的污染地图来确定, 最终确定了307家废气排放企业的分布情况.本文使用的人口分布数据为LandScan 2013数据集, 来源于美国橡树岭国家实验室(http://web.ornl.gov/sci/landscan/index.shtml), 其空间分辨率为0.5″.文中的机场、港口分布数据由Google Earth数据矢量化得到.
由于PM2.5数据和气象数据的监测站点分布、时间分辨率均有所差异, 需要对PM2.5监测数据、气象数据以及VIIRS AOD数据进行时空匹配.在统一坐标系统(Albers正轴等面积割圆投影)的基础上, 以PM2.5站点监测数据为基础, 对VIIRS AOD数据和地面气象资料数据进行空间采样以完成数据的空间匹配. Suomi NPP卫星的过境时间为13:30, 在模型使用VIIRS AOD作为自变量时, 因变量需选取对应卫星过境时刻前后1 h(即13:00和14:00) 的PM2.5年均浓度.对于地面气象资料数据, 依据泰森多边形的原理, 采用最近邻原则进行数据匹配, 取距离PM2.5监测站点最邻近的气象站点观测数据作为该站点的气象自变量.受到气象数据时间分辨率的限制, 每日内同一个站点各时刻气象自变量是相同的.以上数据时空匹配过程借助Python脚本完成, 最终获得345 d数据时空匹配结果, 表现为345条Shapfile监测站点数据, 它们拥有共同的属性表结构, 即各站点名称、投影X Y坐标、PM2.5浓度(包括卫星过境前后1 h平均浓度和日平均浓度)、VIIRS AOD数据和地面气象数据(包括风速、温度、地面相对湿度、降水量).
1.2 模型构建土地利用回归模型(land use regression, LUR)通常能获得高于100 m空间精度的大气污染物空间浓度分布结果, 其被广泛应用于城市尺度的大气污染和流行病学研究.该模型最早是由Briggs于1997年提出[22], 现已广泛用于估计研究区内任意位置的大气污染物浓度.
最小二乘法(ordinary least square, OLS)是计量经济学中常用的一种拟合估算方法, 将自变量与因变量采用全局回归, 从而探究两者之间的关系.而地理加权回归(geographically weighted regression, GWR)模型是由Brunsdon等[23]和Fotheringham等[24]基于非参数建模的思想所提出的用于研究空间非平稳性的新方法.它是对普通线性回归全局模型的扩展, 将数据的地理位置嵌入到回归参数之中, 容许局部而不是全局的参数估计, 其本质上代表对每个观测点分别回归, 因此生成每个区域特有的参数.
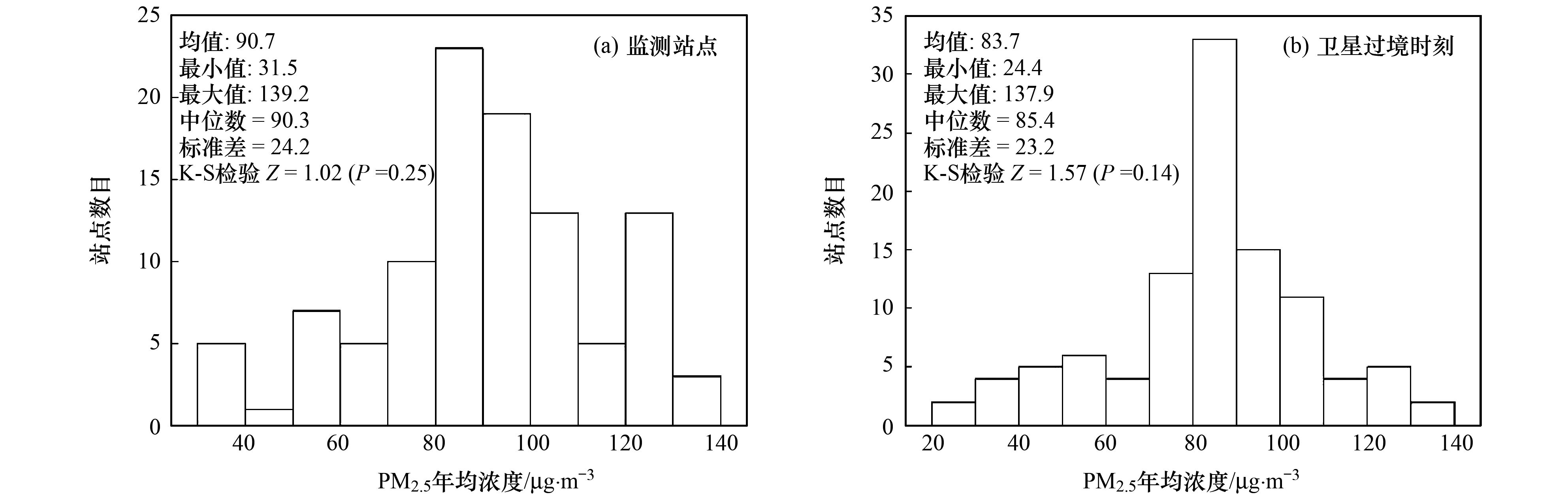
1.2.1 模型变量的生成模型的因变量为京津冀地区104个监测站点的PM2.5监测数据, 本文选取2014年各站点的浓度均值作为模型的因变量, 而模型在使用VIIRS AOD时作为自变量时, 因变量需选取对应卫星过境时刻前后1 h(即13:00和14:00) 的PM2.5年均浓度. 图 2分别是所有监测站点PM2.5年均浓度和卫星过境时刻年均浓度的分布, 两者通过Kolmogorov-Smirnov检验后均近似服从正态分布.
|
图 2 PM2.5年均浓度分布 Fig. 2 Distribution of PM2.5 annual concentration |
模型的自变量共分为7大类, 共包含63个, 用来表征站点周边的交通排放、土地覆被、人口密度因素, 站点所在位置的VIIRS气溶胶光学厚度, 站点到特定污染源等地物的距离, 以及站点所在位置的气象、地形、植被覆盖等可能影响PM2.5浓度的因素.所有自变量均在ArcGIS(ESRI China Inc., Version 10.1) 中生成, 其分类、描述和缓冲区设置如表 1所示.
|
|
表 1 自变量的分类、描述、缓冲区设置以及系数符号假定 Table 1 Classification and description of independent variables, buffer setting, and assumption of coefficient |
1.2.2 模型先验假定和算法设置
自SAVIAH研究[22]之后, 大多数研究都继承了Briggs等所采用的模型先验假定, 本文依据以往研究所描述的各类因素对PM2.5浓度的影响情况, 对各个自变量系数的符号做出如表 1的假定.本文所采用的土地利用回归模型算法参考了文献[25~27]的研究.
地理加权回归模型的执行是在GWR 4.0软件中完成的.各样本的空间坐标选取Albers正轴等面积圆锥投影坐标, 模型的解释变量选取与土地利用回归模型相同的解释变量.空间权重函数选取自适应带宽的高斯(Gaussian)核函数, 带宽设定准则设置为校正的Akaike信息量准则(corrected akaike information criterion, AIC).若模型结果中某一解释变量的全局变量差异标准(diff of criterion)值为正, 则表明其系数在空间上没有显著的分异, 此时将其设置为全局变量重新进行回归, 直到所有系数的全局变量差异标准值均为负值.
1.2.3 模型检验以往研究主要采用交叉检验(cross validation)[28]的方法来判断模型的精度.由于样本数较多, 本研究采用10折交叉验证(10-fold Cross-validation, 10-fold CV)的方法[29, 30], 也有的文献[31, 32]中称之为分组交叉检验(grouped cross-validation, GCV), 即初始采样被随机地平均分割成10个子样本, 一个单独的子样本被保留作为验证模型的数据, 其他9个样本用来训练.交叉验证重复10次, 每个子样本验证一次, 平均10次的结果最终得到一个单一估测.
为了对比添加VIIRS AOD数据后对模型结果的影响, 本研究分别构建包含VIIRS AOD数据和不包含该数据的回归模型.包含VIIRS AOD数据的土地利用回归模型选取对应卫星过境时刻的PM2.5年均浓度作为因变量, 不包含该数据的模型则选取2014年各站点的浓度均值作为模型因变量.采用SPSS 20.0软件利用上述模型算法进行逐步多元线性回归来估计待定参数, 得出回归方程.之后在MATLAB(R2010b)中执行10折交叉验证, 估计模型的精度.
1.2.4 回归映射得到最终回归模型以后, 利用回归方程中各个解释变量系数的空间分布对京津冀地区非监测点位进行污染物浓度的空间模拟, 此过程称为回归映射(regression mapping)[22].回归映射通常利用ArcGIS中的栅格计算器工具实现, 类似于地统计学中的空间插值, 而它能更好地从机理上模拟污染物的空间分异.考虑到研究区的范围大小和各个解释变量的空间分辨率, 将不包含VIIRS气溶胶数据的最小二乘土地利用回归模型和地理加权土地利用回归模型的回归映射的空间分辨率设置为1 km, 将包含VIIRS气溶胶数据的最小二乘土地利用回归模型和地理加权土地利用回归模型回归映射的空间分辨率设置为6 km.若模型中涉及到气象因素, 则参照专业气候数据空间插值软件Anusplin所采用的样条函数法(Spline)[33], 根据京津冀地区的26个气象站点的观测数值进行空间插值, 插值的空间分辨率为1 km.
根据回归方程估计到的污染物浓度通常存在异常值(如存在负值或过高的估计浓度), 根据已有研究[25, 34, 35]本文对回归映射的结果做出如下规定:当某栅格的回归映射结果小于所有监测站点污染物浓度最小值的60%时, 将该栅格的污染物浓度赋为监测站点污染物浓度最小值的60%;当某栅格的回归映射结果超过所有监测站点污染物浓度最大值的20%时, 将该栅格的污染物浓度赋为监测站点污染物浓度最大值的120%.
2 结果与分析 2.1 最小二乘土地利用回归模型利用最小二乘的土地利用回归模型得到的PM2.5年均浓度模型如表 2所示.
|
|
表 2 最小二乘土地利用回归模型结果 Table 2 Results of ordinary least-squares land use regression models |
不添加VIIRS气溶胶数据(模型A)和添加VIIRS气溶胶数据(模型B)的京津冀地区PM2.5年均浓度的最小二乘土地利用回归模型分别为:
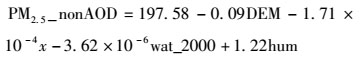
|
(1) |

|
(2) |
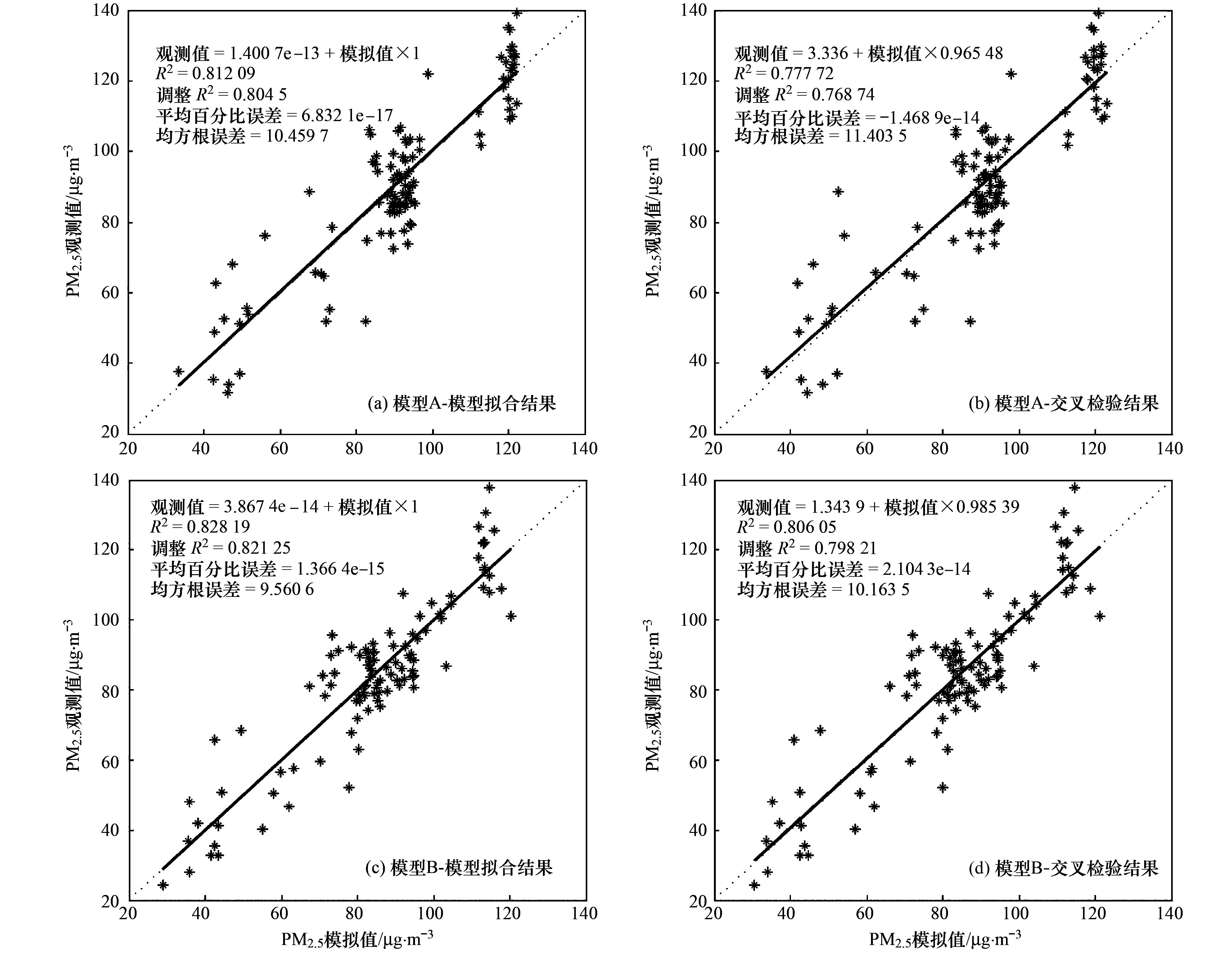
模型A和B的回归散点图如图 3所示, 其中图 3(a)和3(c)分别对应了模型A和B的拟合结果, 图 3(b)和3(d)分别对应了模型A和B的交叉验证结果.对比模型A和B的结果, 可以发现加入VIIRS AOD数据, 模型的拟合优度提升0.76%, 且模型交叉检验的误差略有减小.说明在区域尺度的PM2.5空间分异模拟中, 加入VIIRS AOD数据对于土地利用回归模型的结果会有所提升.
|
图 3 最小二乘土地利用回归模型的回归散点图 Fig. 3 Scatter diagram of ordinary least-squares land use regression models |
运用地理加权土地利用回归模型得到的PM2.5年均浓度模型如表 3所示.
|
|
表 3 地理加权土地利用回归模型结果 Table 3 Results of geographically weighted regression models |
不添加VIIRS气溶胶数据(模型C)和添加VIIRS气溶胶数据(模型D)的京津冀地区PM2.5年均浓度的地理加权土地利用回归模型分别为:
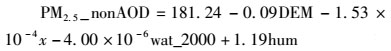
|
(3) |
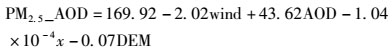
|
(4) |
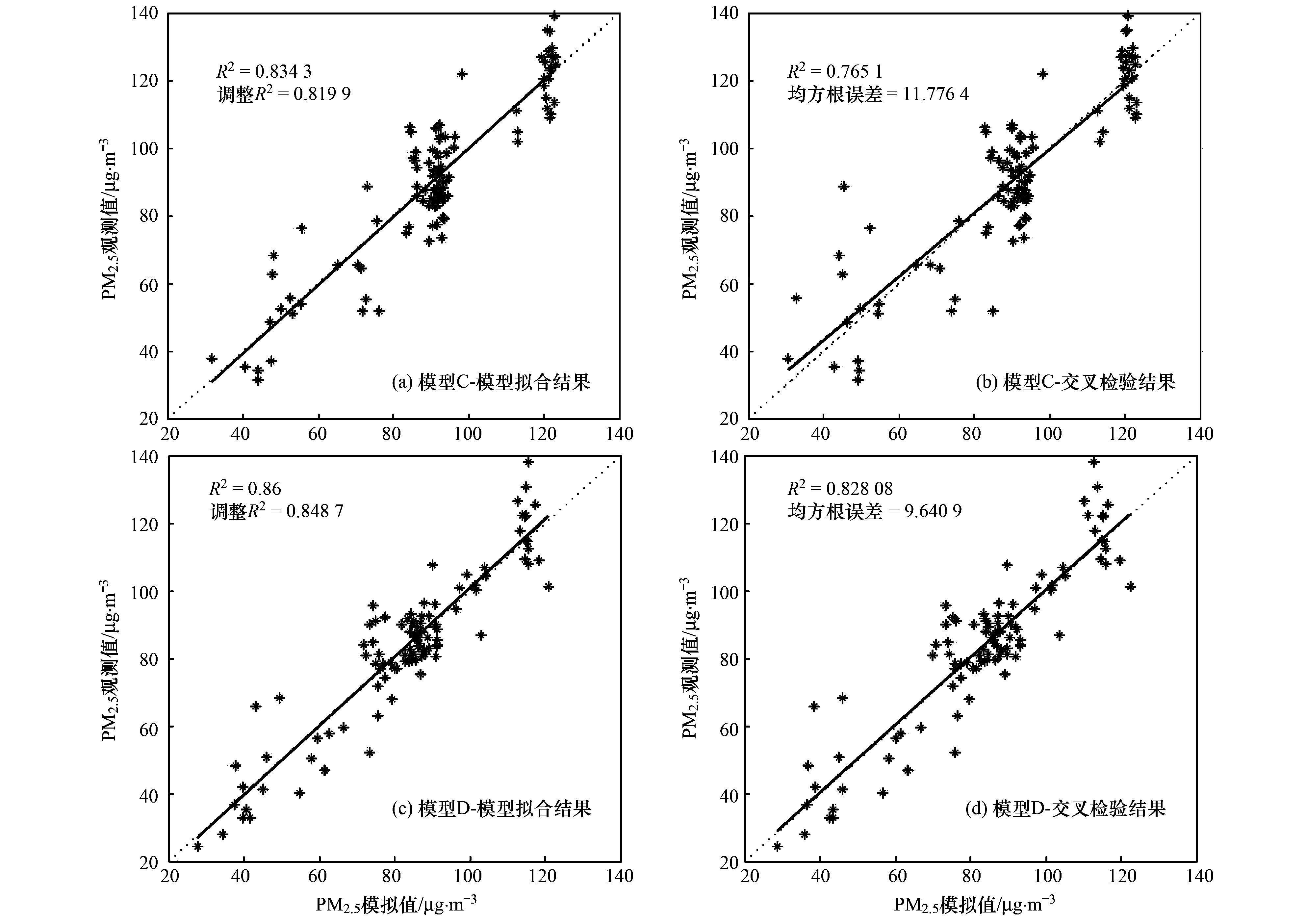
模型C和D的回归散点图如图 4所示, 其中图 4(a)和4(c)分别对应了模型C和D的拟合结果, 图 4 (b)和4(d)分别对应了模型C和D的交叉验证结果.
|
图 4 地理加权土地利用回归模型的回归散点图 Fig. 4 Scatter diagram of geographically weighted land use regression models |
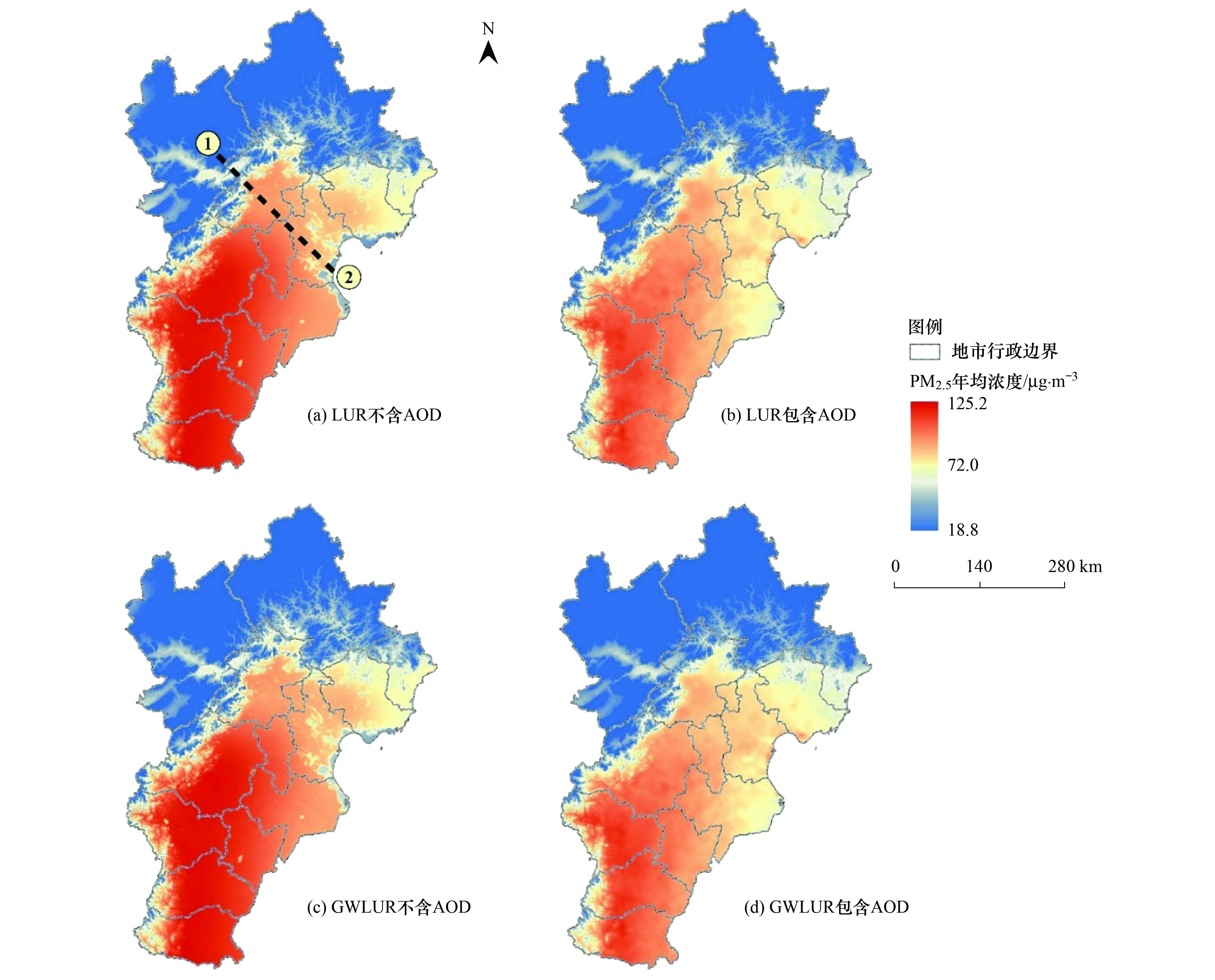
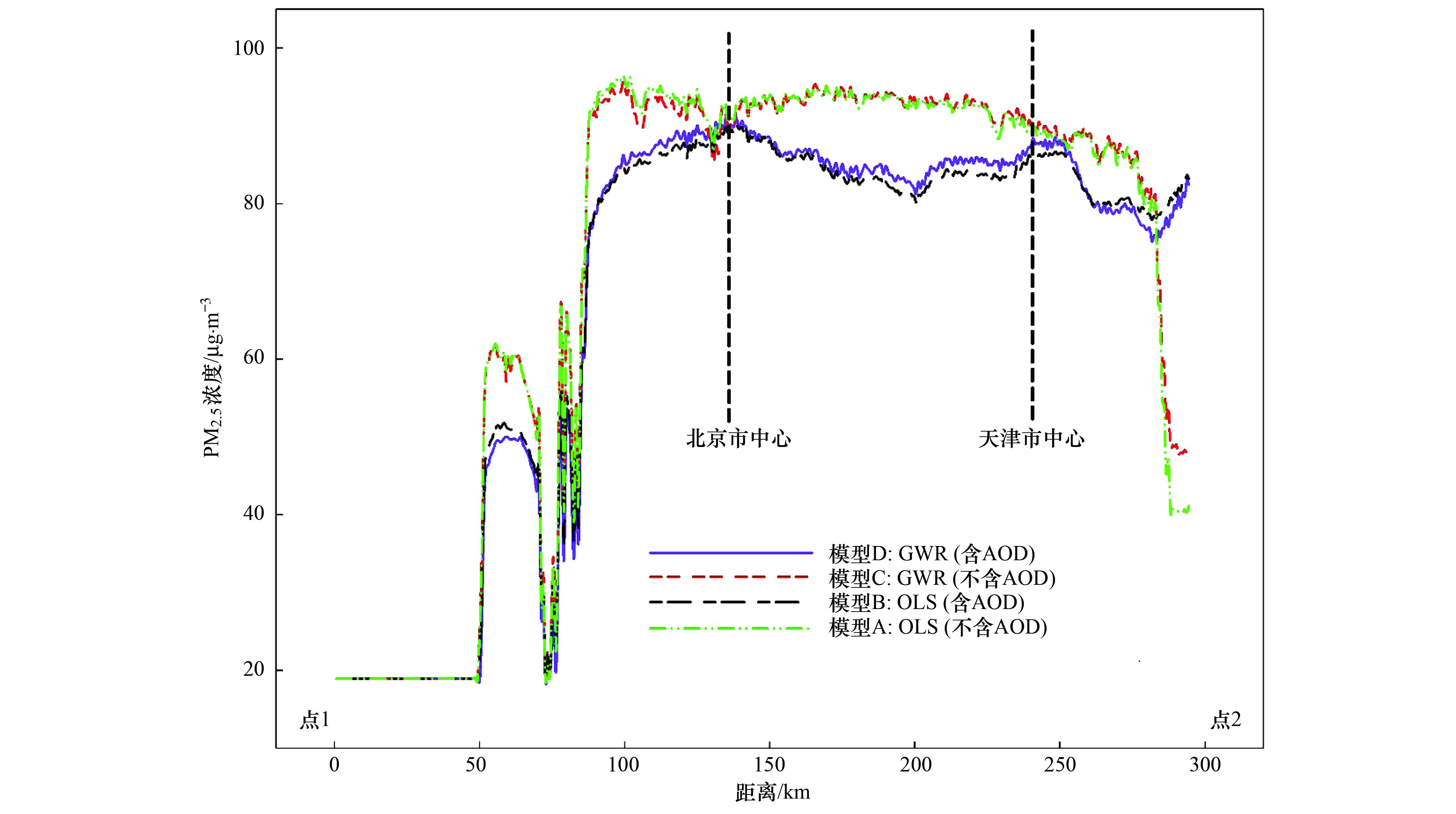
利用上述确定的4个模型得到京津冀地区PM2.5年均浓度空间分异结果如图 5所示.为了更好地呈现京津冀地区PM2.5的空间分异, 选取北京市和天津市中心的连线, 并将其向两端适当延伸, 作为截面线进行PM2.5年均浓度的截面分析. 4个模型在截面线的PM2.5年均浓度分布如图 6所示.
|
图 5 京津冀地区PM2.5年均浓度空间分异结果 Fig. 5 Space variation results of PM2.5 annual concentration in Beijing-Tianjin-Hebei region |
|
图 6 PM2.5年均浓度截面分析图 Fig. 6 Diagram of PM2.5 annual concentration in cross-section analysis |
如图 5所示, 京津冀地区PM2.5年均浓度呈现出很强的空间异质性, 有明显的纬度分异、海陆分异和海拔分异特征.纬度分异特征上, 随着纬度的增加, PM2.5浓度有明显降低; 海陆分异上, 随着到海岸线距离的增加, PM2.5浓度略有增加; 而海拔分异最为明显, 随着海拔的上升, PM2.5浓度显著降低.西南部平原地区PM2.5浓度很高, 是京津冀PM2.5污染的空间热点地区, 主要包括保定市、石家庄市、邢台市、邯郸市和衡水市.该区域地势以平原为主, 农用地和城镇工矿用地占比很高, 生态用地覆盖严重缺失.在区域的工业化、城镇化过程中土地粗放利用, 生态破坏严重, 城镇地区不顾生态环境监管大规模上马较多煤矿开采、钢铁、化工等高污染、高耗能产业, 农村地区乡镇或村办工厂分布广泛而密集, 包括小水泥、小冶金、小化工等企业, 对PM2.5的贡献不容忽视, 这些因素均导致了西南部平原地区PM2.5的高污染.北部山区是京津冀地区PM2.5污染的冷点, PM2.5年均浓度较低, 主要包括了张家口市、承德市和秦皇岛市.该区域地势较高, 自然植被覆盖度较好, 污染产业较少, 旅游业发达, 是京津冀地区的重要生态涵养区.北京和天津两直辖市虽然机动车保有量很高, 人口密集且能源消耗大, 但在该地区率先完成了产业转型升级和能源结构调整, 并将主要的污染企业迁出至周边欠发达地区, 城市化过程配套了较多的生态用地, 因此两直辖市的PM2.5浓度在京津冀地区处于中等偏低水平.
3 讨论对比4个模型得到的回归映射结果可以发现, 图 5所反映的PM2.5浓度空间分异相似程度很高, 并且图 6中各条截面线重合度较大, 说明了不论是否加入VIIRS AOD变量或者是使用地理加权回归的方法, 土地利用回归模型均能较为准确地反映污染物浓度的空间分异.回归映射得到的PM2.5浓度在北部山区存在较多的异常值(多为负值), 本研究对这些异常结果按照观测浓度的最小值进行了修正, 因此图 5中各模型在北部山区的PM2.5浓度差异很小.
4个模型所反映PM2.5浓度空间分布结果的差异主要集中在平原地区. 图 6中, 随着距离的增加, 4条截面线之间的差异明显增大.由于年均浓度模型(模型A和C, 不添加AOD变量)和过境浓度模型(模型B和D, 添加AOD变量)的解释变量不同, 所以两者得到的PM2.5回归映射结果略有差异.比较GWR模型和OLS模型的模拟结果, 图 6中曲线C和D较曲线A和B在平原地区的波动更大, 即PM2.5浓度在地理加权回归模型中所反映的空间分异更为明显, 这充分体现了地理加权回归模型较最小二乘回归更能反映因变量的空间分异的特性.
地理加权回归和最小二乘回归的模型结果对比如表 4所示.对比两者结果可以发现, 模型C较模型A的解释能力提升了1.54%, 交叉检验误差略有提高; 模型D较模型B的解释能力提升了2.74%, 交叉检验R2提升了1.16%, 交叉检验均方根误差减少了0.92 μg·m-3.
|
|
表 4 地理加权回归和最小二乘回归的模型结果对比 Table 4 Comparison between the results of weighted geographically weighted land use regressions and ordinary least-squares land use regression models |
4 结论
(1) 虽然地理加权回归模型的残差仍呈现空间正相关, 但Moran's Ⅰ指数却有了一定程度的下降, 模型的可信度得到了提升, 研究证实地理加权回归模型可以显著降低残差空间自相关性.
(2) 相对于最小二乘回归, 运用地理加权回归的方法能一定程度上提升土地利用回归模型的结果.
(3) 地理加权回归模型较最小二乘回归模型的解释力高, 说明气溶胶光学厚度与PM2.5之间的存在空间异质性, 同时表明在年均PM2.5空间分异模拟上, 地理加权土地利用回归模型最优, 不过该模型存在普适性差的问题; 而最小二乘土地利用回归模型的R2虽然较低, 但是其可以适用于每天的反演, 应用性较广.
| [1] | Peng J, Chen S, Lü H L, et al. Spatiotemporal patterns of remotely sensed PM2.5 concentration in china from 1999 to 2011[J]. Remote Sensing of Environment, 2016, 174: 109–121. DOI: 10.1016/j.rse.2015.12.008 |
| [2] | Han L J, Zhou W Q, Li W F. City as a major source area of fine particulate (PM2.5) in China[J]. Environmental Pollution, 2015, 206: 183–187. DOI: 10.1016/j.envpol.2015.06.038 |
| [3] | Han L J, Zhou W Q, Pickett S T A, et al. An optimum city size? The scaling relationship for urban population and fine particulate (PM2.5) concentration[J]. Environmental Pollution, 2016, 208: 96–101. DOI: 10.1016/j.envpol.2015.08.039 |
| [4] | Yang F, Tan J, Zhao Q, et al. Characteristics of PM2.5 speciation in representative megacities and across China[J]. Atmospheric Chemistry and Physics, 2011, 11(11): 5207–5219. DOI: 10.5194/acp-11-5207-2011 |
| [5] | Du C L, Liu S Y, Yu X, et al. Urban boundary layer height characteristics and relationship with particulate matter mass concentrations in Xi'an, central China[J]. Aerosol and Air Quality Research, 2013, 13(5): 1598–1607. |
| [6] | Tai A P K, Mickley L J, Jacob D J. Correlations between fine particulate matter (PM2.5) and meteorological variables in the United States:implications for the sensitivity of PM2.5 to climate change[J]. Atmospheric Environment, 2010, 44(32): 3976–3984. DOI: 10.1016/j.atmosenv.2010.06.060 |
| [7] | Saide P E, Carmichael G R, Spak S N, et al. Forecasting urban PM10 and PM2.5 pollution episodes in very stable nocturnal conditions and complex terrain using WRF-Chem CO tracer model[J]. Atmospheric Environment, 2011, 45(16): 2769–2780. DOI: 10.1016/j.atmosenv.2011.02.001 |
| [8] | Tanner R L, Bairai S T, Olszyna K J, et al. Diurnal patterns in PM2.5 mass and composition at a background, complex terrain site[J]. Atmospheric Environment, 2005, 39(21): 3865–3875. DOI: 10.1016/j.atmosenv.2005.03.014 |
| [9] | Braniš M, Řezáč ováP, Domasová M. The effect of outdoor air and indoor human activity on mass concentrations of PM10, PM2.5, and PM1 in a classroom[J]. Environmental Research, 2005, 99(2): 143–149. DOI: 10.1016/j.envres.2004.12.001 |
| [10] | Chen Q, Hildemann L M. The effects of human activities on exposure to particulate matter and bioaerosols in residential homes[J]. Environmental Science & Technology, 2009, 43(13): 4641–4646. |
| [11] | Hou Q, An X Q, Wang Y, et al. An evaluation of resident exposure to respirable particulate matter and health economic loss in Beijing during Beijing 2008 Olympic Games[J]. Science of the Total Environment, 2010, 408(19): 4026–4032. DOI: 10.1016/j.scitotenv.2009.12.030 |
| [12] | Zhang A, Qi Q W, Jiang L L, et al. Population exposure to PM2.5 in the urban area of Beijing[J]. PLoS One, 2013, 8(5): e63486. DOI: 10.1371/journal.pone.0063486 |
| [13] | 谢元博, 陈娟, 李巍. 雾霾重污染期间北京居民对高浓度PM2.5持续暴露的健康风险及其损害价值评估[J]. 环境科学, 2014, 35(1): 1–8. Xie Y B, Chen J, Li W. An assessment of PM2.5 related health risks and impaired values of Beijing residents in a consecutive high-level exposure during heavy haze days[J]. Environmental Science, 2014, 35(1): 1–8. DOI: 10.11654/jaes.2014.01.001 |
| [14] | 张衍燊, 马国霞, 於万, 等. 2013年1月灰霾污染事件期间京津冀地区PM2.5污染的人体健康损害评估[J]. 中华医学杂志, 2013, 93(34): 2707–2710. Zhang Y S, Ma G X, Yu F, et al. Health damage assessment due to PM2.5 exposure during haze pollution events in Beijing-Tianjin-Hebei region in January 2013[J]. National Medical Journal of China, 2013, 93(34): 2707–2710. DOI: 10.3760/cma.j.issn.0376-2491.2013.34.006 |
| [15] | 邹滨, 彭芬, 焦利民, 等. 高分辨率人口空气污染暴露GIS空间区划研究[J]. 武汉大学学报(信息科学版), 2013, 38(3): 334–338. Zou B, Peng F, Jiao L, et al. GIS aided spatial zoning of high-resolution population exposure to air pollution[J]. Geomatics and Information Science of Wuhan University, 2013, 38(3): 334–338. |
| [16] | Chu D A, Ferrare R, Szykman J, et al. Regional characteristics of the relationship between columnar AOD and surface PM2.5:application of lidar aerosol extinction profiles over Baltimore-Washington corridor during DISCOVER-AQ[J]. Atmospheric Environment, 2015, 101: 338–349. DOI: 10.1016/j.atmosenv.2014.11.034 |
| [17] | Chudnovsky A A, Koutrakis P, Kloog I, et al. Fine particulate matter predictions using high resolution aerosol optical depth (AOD) retrievals[J]. Atmospheric Environment, 2014, 89: 189–198. DOI: 10.1016/j.atmosenv.2014.02.019 |
| [18] | Schueler C F, Clement J E, Ardanuy P E, et al. NPOESS VIIRS sensor design overview[C]//Proceedings of SPIE 4483, Earth Observing Systems VI, 11. San Diego, CA, USA:SPIE, 2002. |
| [19] | Jackson J M, Liu H Q, Laszlo I, et al. Suomi-NPP VIIRS aerosol algorithms and data products[J]. Journal of Geophysical Research:Atmospheres, 2013, 118(22): 12673–12689. DOI: 10.1002/2013JD020449 |
| [20] | Sayer A M, Hsu N C, Bettenhausen C, et al. Validation and uncertainty estimates for MODIS Collection 6 "Deep Blue" aerosol data[J]. Journal of Geophysical Research:Atmospheres, 2013, 118(14): 7864–7872. DOI: 10.1002/jgrd.50600 |
| [21] | 环境保护部. 环境保护部发布2014年重点区域和74个城市空气质量状况[R/OL]. http: //www. mep. gov. cn/gkml/hbb/qt/201502/t20150202_295333. htm, 2015-02-02. |
| [22] | Briggs D J, Collins S, Elliott P, et al. Mapping urban air pollution using GIS:a regression-based approach[J]. International Journal of Geographical Information Science, 1997, 11(7): 699–718. DOI: 10.1080/136588197242158 |
| [23] | Brunsdon C, Fotheringham A S, Charlton M E. Geographically weighted regression:a method for exploring spatial nonstationarity[J]. Geographical Analysis, 1996, 28(4): 281–298. |
| [24] | Fotheringham A S. Trends in quantitative methods I:stressing the local[J]. Progress in Human Geography, 1997, 21(1): 88–96. DOI: 10.1191/030913297676693207 |
| [25] | Henderson S B, Beckerman B, Jerrett M, et al. Application of land use regression to estimate long-term concentrations of traffic-related nitrogen oxides and fine particulate matter[J]. Environmental Science & Technology, 2007, 41(7): 2422–2428. |
| [26] | Kashima S, Yorifuji T, Tsuda T, et al. Application of land use regression to regulatory air quality data in Japan[J]. Science of the Total Environment, 2009, 407(8): 3055–3062. DOI: 10.1016/j.scitotenv.2008.12.038 |
| [27] | Saraswat A, Apte J S, Kandlikar M, et al. Spatiotemporal land use regression models of fine, ultrafine, and black carbon particulate matter in New Delhi, India[J]. Environmental Science & Technology, 2013, 47(22): 12903–12911. |
| [28] | Hoek G, Beelen R, de Hoogh K, et al. A review of land-use regression models to assess spatial variation of outdoor air pollution[J]. Atmospheric Environment, 2008, 42(33): 7561–7578. DOI: 10.1016/j.atmosenv.2008.05.057 |
| [29] | Mercer L D, Szpiro A A, Sheppard L, et al. Comparing universal kriging and land-use regression for predicting concentrations of gaseous oxides of nitrogen (NOx) for the Multi-Ethnic Study of Atherosclerosis and Air Pollution (MESA Air)[J]. Atmospheric Environment, 2011, 45(26): 4412–4420. DOI: 10.1016/j.atmosenv.2011.05.043 |
| [30] | Novotny E V, Bechle M J, Millet D B, et al. National satellite-based land-use regression:NO2 in the United States[J]. Environmental Science & Technology, 2011, 45(10): 4407–4414. |
| [31] | Amini H, Taghavi-Shahri S M, Henderson S B, et al. Land use regression models to estimate the annual and seasonal spatial variability of sulfur dioxide and particulate matter in Tehran, Iran[J]. Science of the Total Environment, 2014, 488-489: 343–353. DOI: 10.1016/j.scitotenv.2014.04.106 |
| [32] | Tang R, Blangiardo M, Gulliver J. Using building heights and street configuration to enhance intraurban PM10, NOx, and NO2 land use regression models[J]. Environmental Science & Technology, 2013, 47(20): 11643–11650. |
| [33] | 钱永兰, 吕厚荃, 张艳红. 基于ANUSPLIN软件的逐日气象要素插值方法应用与评估[J]. 气象与环境学报, 2010, 26(2): 7–15. Qian Y L, Lv H Q, Zhang Y H. Application and assessment of spatial interpolation method on daily meteorological elements based on ANUSPLIN software[J]. Journal of Meteorology and Environment, 2010, 26(2): 7–15. |
| [34] | Abernethy R C, Allen R W, McKendry I G, et al. A land use regression model for ultrafine particles in Vancouver, Canada[J]. Environmental Science & Technology, 2013, 47(10): 5217–5225. |
| [35] | Wu J S, Li J C, Peng J, et al. Applying land use regression model to estimate spatial variation of PM2.5 in Beijing, China[J]. Environmental Science and Pollution Research, 2015, 22(9): 7045–7061. DOI: 10.1007/s11356-014-3893-5 |
 2017, Vol. 38
2017, Vol. 38

