统计显示,长期PM2.5污染暴露每立方米增加10 μg心脑血管引起的死亡风险增加76%[1]. 有研究显示,人类大约有86.9%的时间是在室内度过[2],人体大部分时间暴露在室内污染物中. 室外颗粒对室内的影响因素有颗粒向室内的传输,沉降过程以及通风方式的影响等.
室内污染与室外环境有着很大的关联性. 在室内无明显污染源的情况下,室外颗粒物的渗透是室内颗粒物的主要来源[3]. 亢燕铭等[4]研究两种空调房间内PM10和PM2.5的浓度变化,研究结果显示PM2.5的室内外颗粒浓度比值I/O均大于PM10的I/O值,表明细颗粒比粗颗粒的穿透性强,更容易通过缝隙进入室内,从而成为室内PM2.5的一个不可忽视的外部源. 张振江等[5]采集天津市某社区室内和室外可吸入颗粒物(PM10)样品,非采暖季和采暖季PM10的室内外浓度比(I/O比值)平均值分别为0.88和0.96,室内外相关系数R2分别为0.32和0.46. 特别在炎热的夏季和寒冷的冬季,尽管门和窗都关着,室外颗粒还是会通过建筑狭缝的缝隙结构如墙缝、 门缝、 窗口细缝以及机械通风系统管道渗透进入室内.
目前国内关于建筑狭缝结构的颗粒渗透传输作用研究还比较少. 近年来研究超细颗粒物渗透传输及其分布方法主要有建立颗粒渗透数学模型分析[6, 7, 8]、 半经验模型[9, 10, 11]、 数值模拟[12,13]、 实验舱模型研究[14,15]和真实建筑环境测量方法[16,17]. Chen等[18]对近年来室内外颗粒浓度相关性做了综述分析,由于颗粒渗透过程中影响因素较多,很多前人研究的结果会有一定差距,且前人多采用中和处理不带电的超细颗粒研究其经过狭缝的渗透情况,对于真实情况各种颗粒经过狭缝的渗透效应研究较少,自然界各种颗粒都带有一定电荷,经过狭缝会产生静电摩擦效应,为了评估室内人体污染物暴露风险,有效减少大气颗粒物污染对人体健康的危害,本文结合前人的研究,采用实验方法和数值模拟方法进一步研究室内超细颗粒经过建筑围护的影响因素及渗透传输机制. 1 材料与方法 1.1 实验装置
实验装置如图 1所示,由实验舱、 狭缝装置、 抽气泵和气体采样仪器FMPS等设备组成. 实验舱和狭缝装置均采用有机玻璃制成,实验舱1尺寸为400 mm×400 mm×400 mm,实验舱2尺寸为270 mm×30 mm×30 mm,中间由狭缝装置连接,实验舱1连接过滤器和颗粒入口,模拟室外环境,实验舱2模拟室内环境,左边连接流量计和抽气泵,通过抽气泵使舱内气体产生流动. 实验舱1顶部安装风扇用以混合舱内颗粒. 舱1和舱2通过三通阀连接快速粒径谱仪(FMPS)用以交替测量两舱内的颗粒数浓度变化. 实验假设狭缝两端温度相同,忽略温度梯度带来的热迁移及热泳效应.
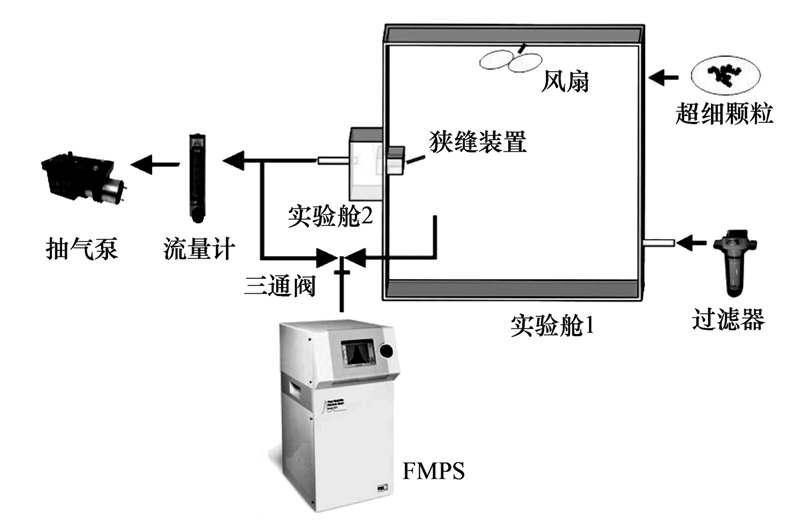 | 图 1 狭缝渗透实验装置示意
Fig. 1 Schematic of experimental setup for slit penetration
|
狭缝装置如图 2所示,是由两块光滑矩形有机玻璃中间两侧各夹1 mm厚的有机玻璃制成的矩形管道,连接处采用专用有机玻璃胶粘贴密封. 缝长z为平行空气流动方向颗粒所经过的距离,缝高d为狭缝高度,缝宽w为狭缝宽度,缝宽相对于缝高和缝长来说很大,可以忽略其对颗粒穿透率的影响. 颗粒物在狭缝中沉积的主要机制有布朗扩散、 重力沉积、 凝并碰撞等作用,其单位时间内布朗运动距离和重力沉降速率与狭缝的尺寸形态有很大关联. 有调查显示,室外空气渗透进入室内,其经过的狭缝高度小于2.5 mm[19],另有研究表明,建筑围护结构其狭缝高度在0.5~7.5 mm之间[20]. 为了方便与其他研究者的结果进行比较,实验选取典型狭缝的尺寸和压差[21],狭缝高度取1 mm,缝长选取43、 94 mm,缝宽选取250 mm,压差分别取4、 10 Pa. 实验所用超细颗粒选取蚊香燃烧颗粒.
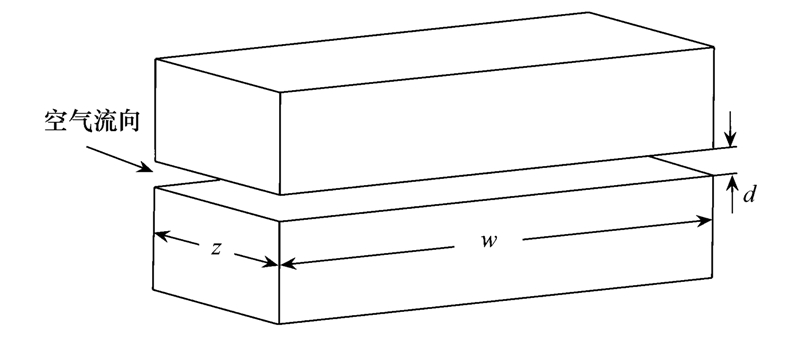 | 图 2 狭缝结构 Fig. 2 Slit structure |
狭缝流动可由风速、 室内外温差、 压差等驱动,当其由压差驱动时,Baker等[20]给出流经狭缝时空气流量Q和压力梯度 Δp的关系,可用方程(1)表示:
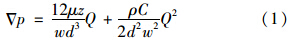
开启实验舱1内的风扇,用以加速气体混合均匀,开启抽气泵,采用流量计控制一定气流量,将蚊香燃烧颗粒直接注入实验舱1,采用FMPS测量其浓度C1,混合均匀数浓度达到106 cm-3量级后停止注入,利用三通阀连接FMPS间隔20 s交替测量两实验舱内浓度变化,实验舱2内浓度为C2. 穿透率P由实验舱2与实验舱1的数浓度比值得到,每个狭缝尺寸装置重复测量3次,每次实验取10组交替测量数值做平均. 1.3 实验仪器
采样分析仪器采用美国TSI公司生产的快速迁移率粒径谱仪(fast mobility particle sizer Spectrometer,FMPS),FMPS是基于EAA(electrical aerosol analyzer)原理的细微颗粒物粒径谱仪,粒径大于1 μm的颗粒经过旋风分离器去除,并可在1 s内达成微粒尺寸分布的分析,即1 s获得一个测量数据,FMPS分32个粒径测量通道涵盖了超细颗粒粒径范围,粒径计数范围为5.6~560 nm,数浓度范围为1~107 cm-3,采样流量为10 L ·min-1. 每次测量前采用HEAP进行清零标定. 2 数值模拟计算 2.1 计算模型建立
前人对狭缝的渗透效应研究多采用实验和理论模型研究,数值模拟计算采用Fluent软件进行研究,由于颗粒相在空气中所占体积比例很小,因此采用分散相模型(discrete phase model,DPM)模拟,通过对大量质点的运动方程进行积分运算获得其运动轨迹及沉积位置. 渗透传输过程流体处于层流状态,颗粒在运动过程中受到多种力的作用,考虑其主要因素如颗粒的重力沉降作用、 布朗扩散过程、 Saffman升力的影响. 颗粒采用稳态粒子跟踪方法,由于分散相所占体积分数较小,只考虑颗粒在已确定连续相流场中的运动,即采用单向耦合求解. 2.2 计算工况及相关算法设置
数值模拟计算工况基于上述实验的相关数据,采用三维模型模拟不同狭缝尺寸、 压差对穿透率的影响. 数值模拟将扩展研究不同缝高及狭缝形状对穿透率的影响,如图 3所示: 矩形截面直管道、 L型管道和U型管道. 相关参数如表 1所示.
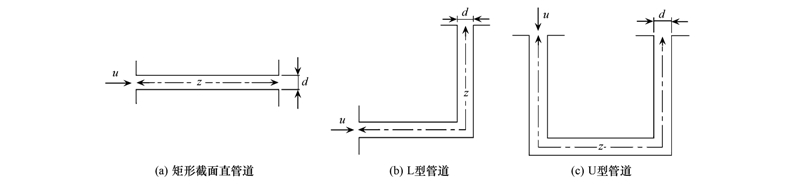 | 图 3 不同形状狭缝管道 Fig. 3 Different shapes of slit pipelines |
| 表 1 实验相关参数 Table 1 AcuteExperimentrelevant parameters |
模拟过程对颗粒相做以下假设: ①颗粒相为球形光滑颗粒(spherical); ②颗粒均不带电,颗粒间不发生静电摩擦、 碰撞凝并、 化学反应; ③对于很多燃烧的气溶胶颗粒如汽车尾气、 工业排放废气等都具有一定黏性,当遇到壁面时会牢固地黏附在表面上,因此设置颗粒遇壁面不反弹,即被捕捉(trap). 分散相颗粒为惰性颗粒(inert-particle),密度取1550 kg ·m-3,颗粒分布采用对数正态分布,粒径范围为对应实验仪器测量范围6~523 nm,分32个粒径段,其质量中位径为200 nm,数浓度取1×105 cm-3. 狭缝两端热力因素按照实验设置,狭缝入口设置为速度入口,出口设置为压强出口,壁面边界采用默认的无滑移条件,内表面颗粒遇到壁面不反弹,即将壁面设置成捕捉类型(trap),出口设置为逃逸类型(escape). 计算跟踪颗粒相对稳定后,穿透率P可由式(2)计算得到.

3 结果与讨论 3.1 狭缝尺寸对穿透率的影响
图 4给出在压差为4 Pa,缝高为1 mm情况下,不同狭缝缝长下各粒径段颗粒的穿透率. 比较实验和数值模拟结果显示,在仪器测量粒径范围内,随着粒径的增加,穿透率呈增加趋势,其影响主导因素为布朗扩散运动,颗粒粒径越小,其扩散系数越大. 模拟结果显示,当粒径大于30 nm,其穿透率接近于1,实验结果小于模拟结果,粒径在10 nm和250 nm附近的颗粒穿透率变化较剧烈,主要是由于10 nm附近的超细颗粒极不稳定,在短暂时间内迅速碰撞变成较大粒径颗粒,250 nm附近颗粒数量较少,误差较大. 缝长越长,颗粒穿透率越小,这是因为缝长增加则增加了颗粒在狭缝内的停留时间[22],从而增加了颗粒与壁面的碰撞几率. 实验结果相比模拟结果其整体趋势相近似,但实验结果偏小,这可能是因为自然界各种颗粒都带有一定电荷,经过狭缝会产生静电摩擦效应,从而对颗粒穿透有一定影响,同时颗粒在气体管道输送过程中也会有一定的损失. 由于所选颗粒为真实环境燃烧的蚊香颗粒,未对颗粒进行中和处理,结果与Liu[21]研究结果相比略小,但趋势基本吻合.
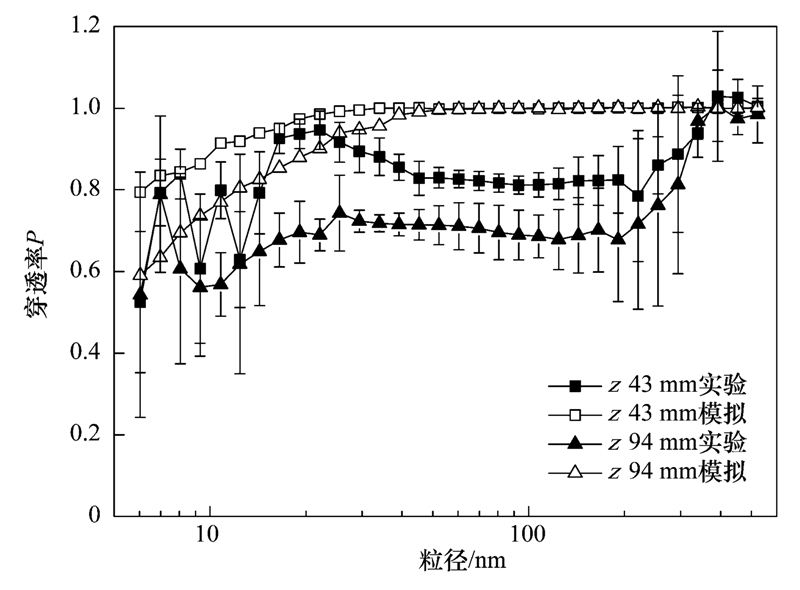 | 图 4 不同缝长下各粒径段颗粒的穿透率 Fig. 4 Penetration rates of particles with different sizes at different slit lengths |
由于实验装置加工及仪器测量范围有一定的限制,借助数值模拟方法扩展研究缝高对穿透率P的影响,结果如图 5(a)所示,在重力与布朗运动扩散、 Saffman升力的综合作用下,缝高越小,增加了颗粒与壁面的碰撞几率,从而穿透率越小. 随着粒径增大,穿透率呈增加趋势,而当缝高减小到0.25 mm时,粒径在300 nm附近颗粒穿透率达到最高0.93,随粒径继续增加,穿透率出现拐点,颗粒穿透率呈减小趋势. 去除重力的作用,如图 5(b)所示,在缝高为0.25 mm时,穿透率未出现拐点,而是随粒径增加呈增加趋势,结果表明,当粒径大于300 nm时,重力沉降开始起主导作用,在重力沉降和布朗运动的双重作用下颗粒穿透率开始降低. 当缝高变化时,不同粒径颗粒沉降到壁面的主导因素随之变化,这与单位密度球体单位时间内由布朗运动和重力引起的净位移有关[23],当缝高减小时,逐渐接近颗粒净位移,颗粒更容易碰到壁面被捕捉,如表 2给出部分粒径颗粒单位密度球体1 s内布朗运动和重力引起的净位移. 在粒径为10 nm时,布朗运动均方根位移与重力沉降位移比值xBM/xgrav达4.88×103,以布朗运动为主,随粒径增大,其位移比值xBM/xgrav降低,重力开始起主导作用,当颗粒粒径为1 μm时,位移比值xBM/xgrav只有0.21. 狭缝尺寸中缝高对穿透率影响最大,占主导影响因素.
| 表 2 单位密度球体1 s内布朗运动和重力沉降净位移 Table 2 Brownian motion within 1 s and gravity settling net displacement of unit density sphere |
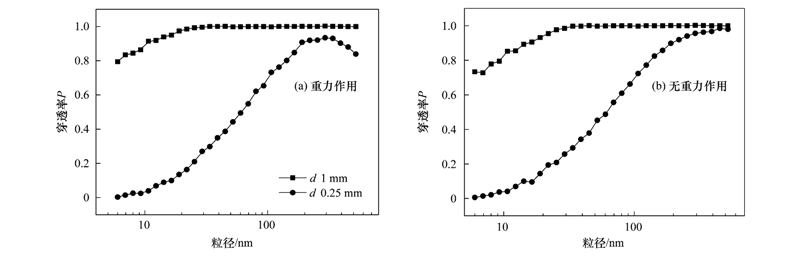 | 图 5 不同缝高下颗粒的穿透率的模拟结果 Fig. 5 Simulation results of particle penetration rates at different slit heights |
图 6给出缝长为43 mm、 缝高为1 mm的狭缝装置在压差分别为4、 10 Pa下的颗粒穿透率,将实验结果与数值模拟结果进行比较,模拟结果均略大于实验结果,数值模拟结果显示粒径小于30 nm的颗粒穿透率随压强增大而增大,当粒径大于30 nm,穿透率均接近于1. 实验结果显示,不同压差结果无明显区别,在一定范围内,较小压差对颗粒穿透率影响较小.
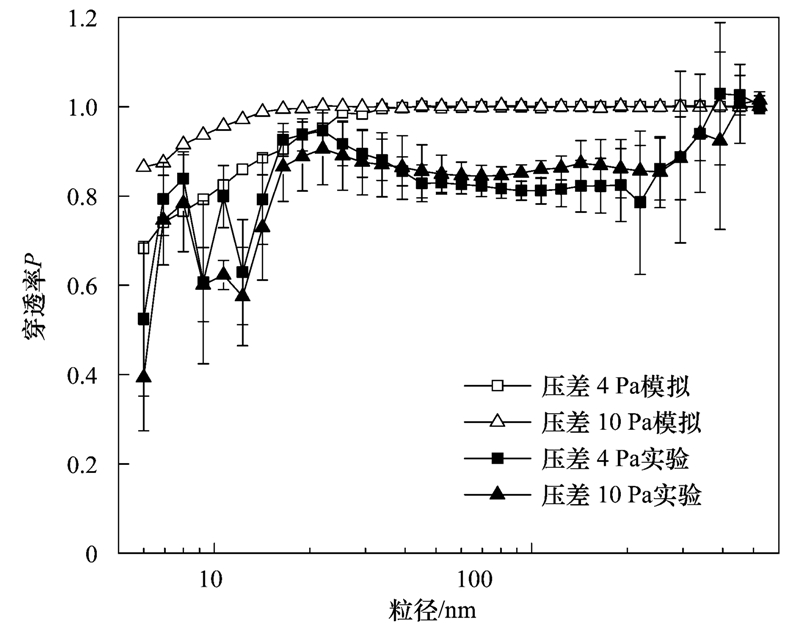 | 图 6 不同压差下颗粒穿透率 Fig. 6 Particle penetration rates under different inlet pressures |
数值模拟方法扩展研究不同狭缝形状对穿透率P的影响,狭缝缝长均为43 mm,缝高1 mm,压差4 Pa,结果如图 7所示,不同狭缝形状对粒径小于35 nm的颗粒穿透率影响较大,L型和U型穿透率接近,均小于矩形直通道.
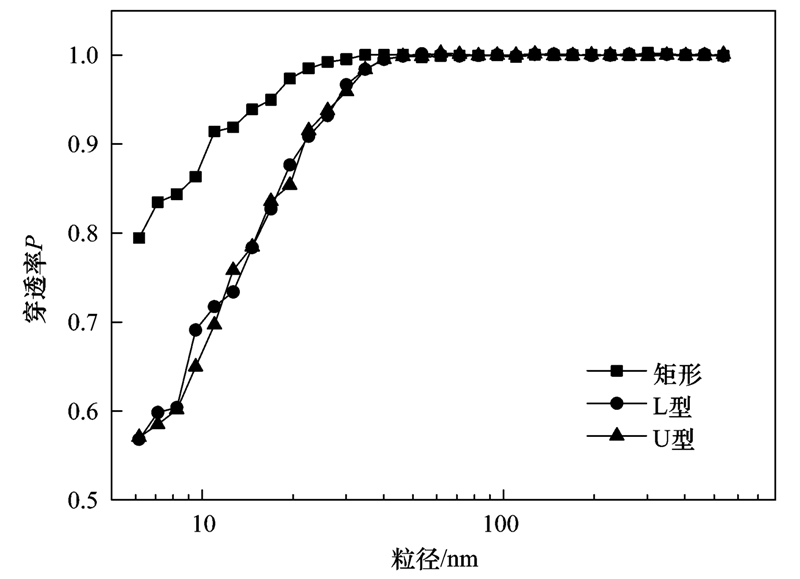 | 图 7 不同狭缝形状下颗粒穿透率的模拟结果 Fig. 7 Simulation results of particle penetration rates in slit with different shapes |
图 8为实验所测实验舱1(室外)和实验舱2(室内)的颗粒数浓度和穿透率随时间的变化,其狭缝缝长为43 mm,缝高为1 mm,压差为4 Pa. 结果显示,颗粒粒径为45.3~294.3 nm的颗粒数浓度随时间衰减迅速,其中粒径为107.5 nm的颗粒衰减最快. 其穿透率P随时间变化波动较小,穿透率P随粒径增大,有增加趋势. 在较低浓度一定范围内,颗粒数浓度对穿透率的影响较小,
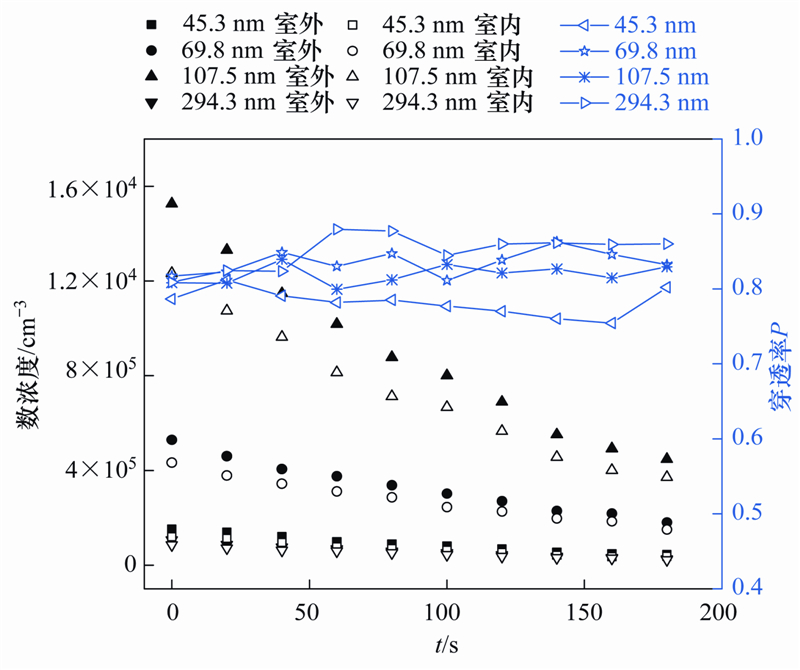 | 图 8 室内外不同粒径颗粒数浓度和穿透率P随时间变化趋势 Fig. 8 Trends of indoor and outdoor numerical concentration of particles with different sizes and penetration rate P over time |
与其粒径有关,根据室外空气各粒径段颗粒数浓度可以大概估算室内空气质量品质. 图 9给出室内外颗粒随时间的粒径谱分布,颗粒粒径主要分布在100 nm附近,该粒径段颗粒数浓度变化最明显. 随时间变化,颗粒数量中位径(CMD)向小粒径转移.
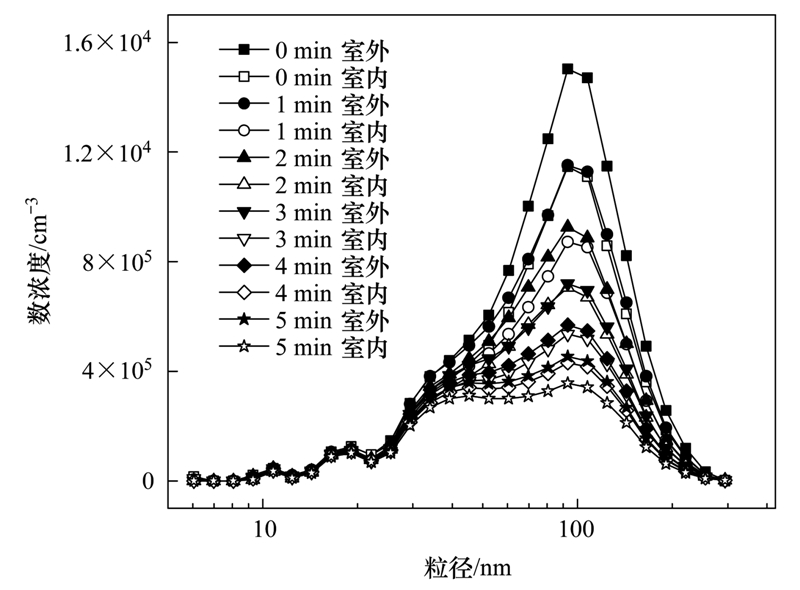 | 图 9 室内外颗粒粒径谱随时间分布 Fig. 9 Distribution of indoor and outdoor particle size spectra over time |
如图 10为不同狭缝尺寸及压差下实验所测舱1(室外)和舱2(室内)颗粒数浓度,其狭缝高度均为1 mm,结果显示室内外颗粒数浓度呈线性相关性,超细微粒I/O比值为0.69~0.73,这与Tippayawong等[24]在学校区域得到的超细微粒I/O比值0.69~0.8相近,Massey等[25]也给出了路边、 乡村和城市的室内外颗粒质量浓度回归曲线,PM0.5斜率分别为0.98、 0.47和0.74. 相关系数R2能很好地表征室内外颗粒的关联程度[26],相关系数R2均到达0.99以上,表明室内颗粒物浓度很大程度上与室外颗粒的渗透有关. 在实际应用环境中人们可以根据室外颗粒浓度来预测室内颗粒浓度,从而评估室内人体污染物暴露风险,有效减少大气颗粒物污染对人体健康的危害.
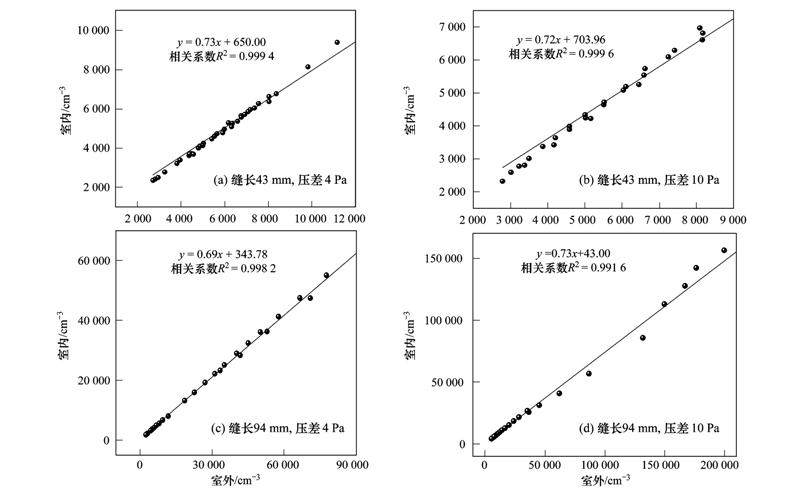 | 图 10 室内外颗粒数浓度相关性分析 Fig. 10 Correlation analysis of indoor and outdoor particle numerical concentrations |
(1)在仪器测量粒径范围内,实验和数值模拟结果显示,当缝高为1 mm,随着颗粒粒径的增加,穿透率呈增加趋势,缝长越长,缝高越小,颗粒穿透率就越小. 模拟计算结果表明当粒径大于30 nm,其穿透率接近于1,而当缝高减小到0.25 mm时,粒径在300 nm附近颗粒穿透率达到最高0.93,随粒径继续增加,颗粒穿透率呈减小趋势,重力沉降开始逐渐占主导因素. 当缝高变化时,不同粒径颗粒沉降到壁面的主导因素随之变化,这与单位密度颗粒单位时间净位移有关. 实验结果显示,粒径在10 nm和250 nm附近的颗粒穿透率变化较剧烈,小粒径颗粒穿透率较小,其影响主导因素为布朗扩散运动. 实验结果相比模拟结果偏小,但其整体趋势相一致.
(2)缝长为43 mm、 缝高为1 mm的狭缝装置在不同压差下其模拟结果均略大于实验结果,数值模拟结果显示粒径小于30 nm的颗粒穿透率随压强增大而增大,当粒径大于30 nm,穿透率接近于1. 实验结果显示,在一定范围内,压差对颗粒穿透率影响较小. 狭缝形状只对粒径小于35 nm的颗粒有影响,其直通道颗粒穿透率大于有拐角的通道穿透率. 狭缝颗粒的渗透传输机制与过滤器的过滤机制相类似,该结论可以为过滤器和空气净化器的研究提供一定参考价值.
(3)颗粒数浓度随时间衰减迅速,而其穿透率P随时间变化波动较小. 在一定范围内,颗粒数浓度对穿透率的影响较小. 室内外颗粒数浓度I/O比值范围为0.69~0.73,相关系数R2达0.99,线性相关性显著.
| [1] | Miller K A, Siscovick D S, Sheppard L, et al. Long-term exposure to air pollution and incidence of cardiovascular events in women[J]. The New England Journal of Medicine, 2007, 356 (5): 447-458. |
| [2] | Klepeis N E, Nelson W C, Ott W R, et al. The national human activity pattern survey (NHAPS): a resource for assessing exposure to environmental pollutants[J]. Journal of Exposure Analysis and Environmental Epidemiology, 2001, 11 (3): 231-252. |
| [3] | 程鸿, 胡敏, 张利文, 等. 北京秋季室内外PM2.5污染水平及其相关性[J]. 环境与健康杂志, 2009, 26 (9): 787-789. |
| [4] | 亢燕铭, 钟珂, 柴士君. 上海地区空调房间夏季室内外颗粒物浓度变化特征[J]. 过程工程学报, 2006, 6 (Z2): 46-50. |
| [5] | 张振江, 赵若杰, 曹文文, 等. 天津市可吸入颗粒物及元素室内外相关性[J]. 中国环境科学, 2013, 33 (2): 357-364. |
| [6] | Liu D L, Nazaroff W W. Modeling pollutant penetration across building envelopes[J]. Atmospheric Environment, 2001, 35 (26): 4451-4462. |
| [7] | 田利伟. 室内环境颗粒物浓度预测模型及污染控制策略研究[D]. 长沙: 湖南大学, 2009. 44-55. |
| [8] | Tian L W, Zhang G Q, Lin Y L, et al. Mathematical model of particle penetration through smooth/rough building envelop leakages[J]. Building and Environment, 2009, 44 (6): 1144-1149. |
| [9] | Jeng C J, Kindzierski W B, Smith D W. Particle penetration through inclined and L-shaped cracks[J]. Journal of Environmental Engineering, 2007, 133 (3): 331-339. |
| [10] | Lai A C K. Modeling indoor coarse particle deposition onto smooth and rough vertical surfaces[J]. Atmospheric Environment, 2005, 39 (21): 3823-3830. |
| [11] | Wood N B. A simple method for the calculation of turbulent deposition to smooth and rough surfaces[J]. Journal of Aerosol Science, 1981, 12 (3): 275-290. |
| [12] | Zhang Z, Chen Q. Comparison of the eulerian and lagrangian methods for predicting particle transport in enclosed spaces[J]. Atmospheric Environment, 2007, 41 (25): 5236-5248. |
| [13] | 张帆. 大气悬浮颗粒物对建筑围护结构穿透机理的数值模拟[D]. 长沙: 湖南大学, 2007. 37-49. |
| [14] | Mosley R B, Greenwell D J, Sparks L E, et al. Penetration of ambient fine particles into the indoor environment[J]. Aerosol Science and Technology, 2001, 34 (1): 127-136. |
| [15] | Liu D L, Nazaroff W. Particle penetration through building cracks[J]. Aerosol Science and Technology, 2003, 37 (7): 565-573. |
| [16] | Tung T C W, Chao C Y H, Burnett J. A methodology to investigate the particulate penetration coefficient through building shell[J]. Atmospheric Environment, 1999, 33 (6): 881-893. |
| [17] | Chao C Y H, Wan M P, Cheng E C K. Penetration coefficient and deposition rate as a function of particle size in non-smoking naturally ventilated residences[J]. Atmospheric Environment, 2003, 37 (30): 4233-4241. |
| [18] | Chen C, Zhao B. Review of relationship between indoor and outdoor particles: I/O ratio, infiltration factor and penetration factor[J]. Atmospheric Environment, 2011, 45 (2): 275-288. |
| [19] | Thomas D A, Dick B A. Air infiltration through gaps around windows[J]. Journal of the Institution of Heating and Ventilating Engineers, 1953, 21 : 85-97. |
| [20] | Baker P H, Sharples S, Ward I C. Air flow through cracks[J]. Building and Environment, 1987, 22 (4): 293-304. |
| [21] | Liu D L. Air pollutant penetration through airflow leaks into buildings[D]. Berkeley: University of California, 2002. 66-71. |
| [22] | Xu B, Liu S S, Zhu Y F. Ultrafine particle penetration through idealized vehicle cracks[J]. Journal of Aerosol Science, 2010, 41 (9): 859-868. |
| [23] | Hinds W C. Aerosol technology: properties, behavior, and measurement of airborne particles [M]. (2nd ed.). United States of America: John Wiley & Sons Inc, 1999. 156-160. |
| [24] | Tippayawong N, Khuntong P, Nitatwichit C, et al. Indoor/outdoor relationships of size-resolved particle concentrations in naturally ventilated school environments[J]. Building and Environment, 2009, 44 (1): 188-197. |
| [25] | Massey D, Masih J, Kulshrestha A, et al. Indoor/outdoor relationship of fine particles less than 2.5 μm (PM2.5) in residential homes locations in central Indian region[J]. Building and Environment, 2009, 44 (10): 2037-2045. |
| [26] | Colome S D, Kado N Y, Jaques P, et al. Indoor-outdoor air pollution relations: particulate matter less than 10 μm in aerodynamic diameter (PM10) in homes of asthmatics[J]. Atmospheric Environment. Part A. General Topics, 1992, 26 (12): 2173-2178. |
 2015, Vol. 36
2015, Vol. 36

