2. 中国环境科学研究院环境基准与风险评估国家重点实验室, 北京 100012
2. State Key Laboratory of Environmental Criteria and Risk Assessment, Chinese Research Academy of Environmental Sciences, Beijing 100012, China
铅酸蓄电池污染场地是工业污染场地一个重要类型[1,2],赋存在场地土壤中的铅对人体健康和生态环境产生严重危害[3]. 近年来,由生产过程和工业搬迁等原因产生的铅酸蓄电池污染场地数量呈现上升趋势[4]. 部分污染场地土地利用类型也由此发生变化,已有大量场地进入到环境调查、风险评估和修复治理过程[5, 6, 7]. 在此过程中,污染物在场地的空间分布范围是进行场地风险管理的重要基础[8],基于土壤采样点数据,采用空间统计模型对污染物空间分布预测是目前描述污染物空间分布的主要手段[9,10].
铅酸蓄电池企业在生产过程中涉及到重金属,对场地内土壤产生严重的Pb污染,受历史生产过程、车间工艺布局、污染源分布等因素影响,同其它工业污染场地类似,土壤中污染物的累积较多地受人为因素干扰,局部区域污染严重,污染物含量极高,不同区域污染物的污染程度和分布规律都不相同[11,12]. 受异常值影响,土壤中污染物具有很强的空间变异性[13,14],在受到人为干扰较大的地区,污染物含量与土壤属性等环境变量不具有很高的相关性[15]. 对于土壤污染中高值点的空间分布,现有研究大多采用数值模型或空间模拟的方法来表征污染物空间分布规律[16],插值计算中需要土壤性质等辅助信息且输入参数较多,对于受人为干扰因素较大的工业污染场地表层土壤污染分布表征,有些数据并不容易获取,因此插值的精度会受建模方法和参数准确性的影响较大.
现有空间插值模型针对较大尺度面源土壤污染预测效果较好,在使用时对数据统计分布特征、样本量和采样方案以及相关环境辅助数据都有一定要求. Li等[17]系统分析了空间统计模型、确定性插值模型等不同插值方法的应用机制和适用条件. 不同模型的模型精度优势和插值效果并不一致[18,19]. 为进一步提高土壤中污染物空间分布预测精度,相关学者提出了地理加权回归和贝叶斯最大熵模型,在反映空间变异特征等方面取得了较好的效果[20,21]; 同时在数据挖掘[22]、不同抽样方案[23]、引入环境数据[24]等方面也展开了提高预测精度相关内容的研究. 本研究针对该目标污染场地土壤Pb含量强变异性的分布特点,采用数据拆分后分区预测的思路,分别表征反映局部高污染区域真实高值点数据集部分和反映整体污染特征其它数据集部分的污染范围,将两部分数据集采用三角网格和对数克里格模型分别插值计算后叠加处理,并对预测结果与常用的地统计学模型和确定性插值模型进行对比,分析不同模型的精度优势和对污染评价结果的影响,弥补现有插值模型对高偏倚性数据集预测的不足,以期为此类污染场地的环境风险管理工作提供科学指导. 1 材料与方法 1.1 目标污染场地概况
该场地曾经是我国西南地区较大的铅酸蓄电池生产厂家,有60多年生产历史,生产产品有各类型铅酸蓄电池,广泛应用于交通、能源、通信等蓄能要求领域. 原厂区有生产车间、污水处理站、包装车间、机修车间以及废铅堆放区等功能区域,该厂区平面布置图如图 1所示. 生产的主要原材料有铅、锌、硫酸等,在生产过程中涉及到重金属污染物,通过场地初步调查,发现Pb为该场地的特征污染物. 根据场地的水文地质资料和钻孔显示,场区地层为第四系全新统素填土(Qml4)、残坡积粉质黏土层(Qel+dl4).
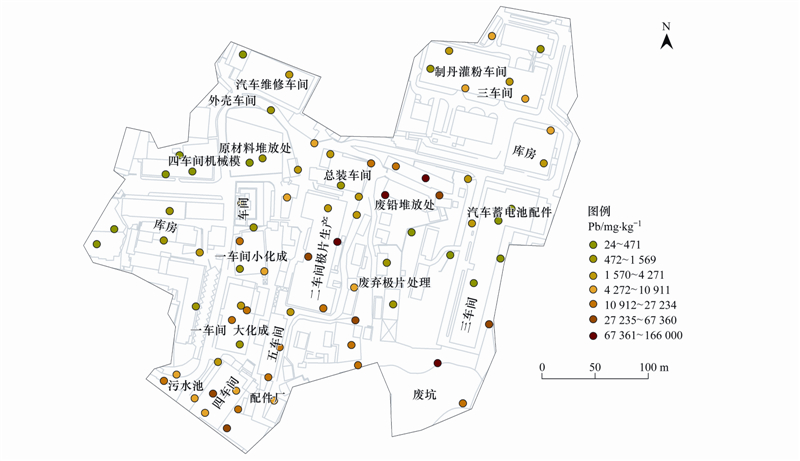 | 图 1 厂区平面布置和样点分布示意 Fig. 1 Factory floor plan and locations of sampling sites |
目标场地面积为13.6 hm2,通过对目标场地的勘察,结合该厂区车间布局以及生产管理等因素影响,现场采样采用随机布点和判断布点相结合的原则,对已察明的重污染区域和已知污染区域加密布点,共布设土壤样点79个,采样深度为0~9.4 m,本研究选择表层土壤即0~60 cm深度土壤样点进行分析. 因场地搬迁与拆除造成部分建筑垃圾堆砌在地面,钻孔采样采用挖掘机和钻机相结合的方式,在预先设定的采样点位钻探,获取该点位的土柱样品,将采样管移出地面后,将筛选出的土样混合均匀后立即装入250 mL直口玻璃瓶中,并正确密封、填写标签、放入装有适量低温蓝冰的保存箱中,样品采集完毕后送回实验室并进行检测. 土壤中Pb含量采用USEPA 6010C-2007方法进行测定[25].
1.3 不同插值方法介绍本研究采用4种不同插值模型对土壤中Pb污染进行空间分布预测. 通过对原始样点含量数据值初步统计分析可知,数据集具有严重偏倚特征,且含有异常值. 对于正态分布数据集,大概99.7%的样本值落在距平均值和3个标准差范围内,由于本研究中的高值点含量极大,因此本研究采用①平均值加4倍标准差的方法来识别异常值,识别出异常值后,对异常值进行拆分,并以原始数据的中值代替拆分出的高值,对于高值点部分,采用三角网格插值方法(TIN)进行预测,对于拆分出高值点后的数据集,符合对数正态分布特征,采用对数克里格方法(OKLG)进行预测,最后对两部分预测结果叠加处理,形成整个场地的污染分布预测. 使用对偏斜数据正态分布变换效果较好的BOX-COX方法对原始数据做正态变换处理,然后使用②普通克里格(OKBC)以及③确定性插值模型中的反距离加权方法(IDW)和样条函数方法(Spline)对正态变换后的数据插值计算,将插值后的结果根据正态变换公式进行逆变换,转换到原始数据单位. 最后对4种模型的预测精度和污染评价进行对比分析.
1.4 数据处理方法本研究中Pb含量的描述性统计分析采用软件SPSS 16.0,空间变异分析采用地统计学软件GS+7.0,空间插值计算与污染评价采用地理信息系统软件ESRI ArcGIS 10.0. 不同插值方法预测结果精度验证采用交叉验证法中常用的评价指标平均误差(ME)和均方根误差(RMSE)进行评价[26],ME越接近于0,RMSE越小表明插值精度就越高.
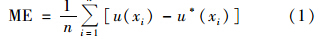
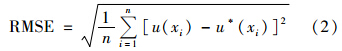
场地土壤中Pb含量的频率分布特征如图 2所示,可以看出,由于Pb含量数据中有真实高值点存在,其频率分布直方图具有很大的右偏斜,不符合正态分布特征. 约有75%的样点含量集中在23.60~8000 mg ·kg-1范围内. 最大值为166000 mg ·kg-1,最小值为23.60 mg ·kg-1,样点含量的极差很大. 描述性统计指标中的标准差为26970.67 mg ·kg-1,偏度为3.57,峰度为14.87,变异系数为1.95,表明原始样点含量数据具有很强的空间变异特征. 采用平均值加4倍标准差的方法识别数据集中高值点,共发现有9个异常真实高值点存在,将这9个异常真实高值点用中值代替后再进行描述性统计分析,发现新数据集的偏度、峰度以及变异系数都明显降低,基本符合对数正态分布特征,表明真实高值点是原始数据集产生严重右偏倚性的主要原因. 将采样样点叠加到原厂区平面分布图上可以看出,真实高值点以及超标较为严重的样点分布区域包括废铅堆放区,五车间和配件厂、二车间、一车间和四车间等,说明上述车间在生产过程中对土壤中Pb的累积影响较大. 样点含量数据的均值和中值分别为13839.83 mg ·kg-1和2855 mg ·kg-1,远超过北京住宅用地标准中的400 mg ·kg-1,目标场地已经存在较大的环境风险.
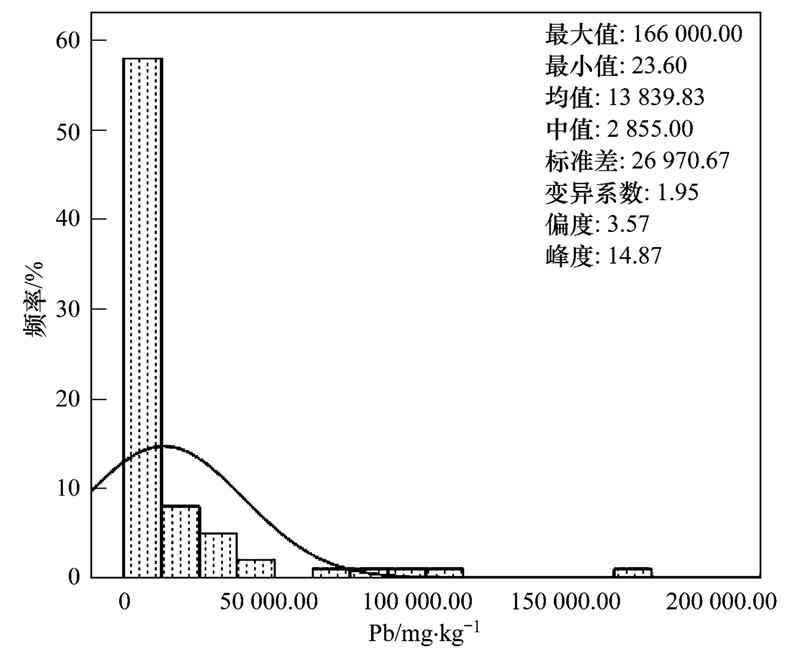 | 图 2 场地土壤中Pb含量频率分布直方图 Fig. 2 Frequency distribution of soil Pb |
该目标污染场地是我国典型的铅酸蓄电池生产企业,部分车间生产以及材料的存放过程中对局部区域产生较严重的土壤Pb污染,样点含量含有异常真实高值,造成样点污染物数据在场地中具有很强的空间变异性以及分布的不连续特征. 从原始样点Pb含量数据的描述性统计分析结果已经看出,原始数据集具有很强的偏倚性和离散特征. 本研究采用泰森多边形的方法来进一步揭示土壤中Pb污染的空间变异,分析采样样点间的相似性和局部变化特征. 采用土壤钻孔样点构建整个场地的泰森多边形,并依据每个样点的含量计算每个多边形的标准差和平均值,来确定多边形的变异系数(coefficient of variation,CV),对所有多边形变异系数值统计得出最小值为0.51,最大值为2.58,均值为1.27,标准差为0.48,计算出的土壤钻孔样点含量变异系数分布如图 3所示,从中可以看出,土壤中Pb污染的变异程度较强,空间变异系数在场地的中部区域较高,其它区域相对较低. 土壤中Pb污染的局部变异系数特征与原厂区生产车间产生污染源的分布情况较为一致,场地的中部区域主要为废铅堆放区,五车间和配件厂、二车间、一车间和四车间等,是产生土壤Pb污染的主要来源,在该区域的采样样点含量都较高,且含有真实高值点,造成了污染物在空间上强的空间变异性,因此污染物含量的空间变异系数值也较大. 其它区域主要有库房、成品车间、办公楼以及配件厂等,对土壤的Pb污染较轻,污染物的分布相对较为连续,污染物含量的空间变异系数值较小. 局部变异系数值较大的地方,是将来需要加密采样以及修复治理等相关工作重点关注的区域. 通过分析土壤中Pb含量的空间变异分布特征,可以直观获取污染物在空间上的离散特性和离散程度,对选择合理的插值方法,辅助分析污染评价结果具有重要作用.
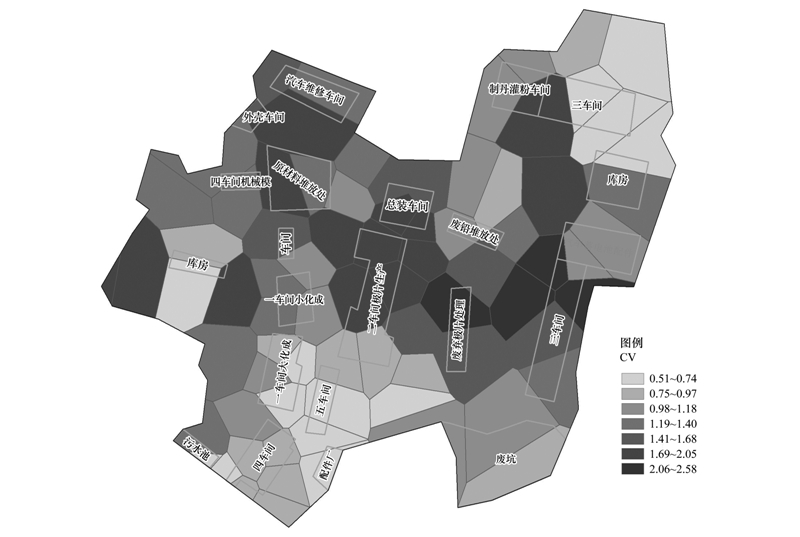 | 图 3 土壤中Pb含量的空间变异特征 Fig. 3 Spatial variation of Pb concentration in soil of part regions |
对拆分后的数据集做对数正态变换以及原始数据集做BOX-COX正态变换,两种正态变换后数据的描述性统计分析结果及频率分布直方图如图 4所示,可以看出,经正态变换后,两种数据集的偏度和峰度均有较大程度降低,能够通过正态分布检验,频率分布直方图显示符合正态分布特征.
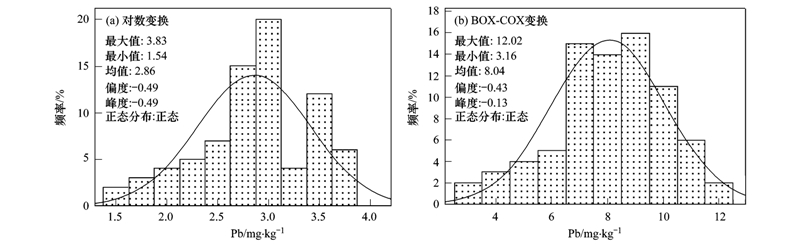 | 图 4 数据正态变换后频繁分布直方图 Fig. 4 Histograms of Pb concentrations in soils after normality transformation |
对正态变换后的数据集进行半变异函数拟合,拟合的最优理论模型和参数如表 1所示,两种数据正态变换后数据拟合的半变异函数理论模型分别符合指数和高斯模型,空间相关度分别为0.53和0.50,表明正态变换后的数据具有中等程度相关性,拟合的决定系数分别为0.96和0.82,具有较为稳健的效果,能够满足对数克里格和普通克里格插值要求.
|
|
表 1 半变异函数模型参数 Table 1 Parameters of variogram models |
4种方法预测后的交叉验证结果精度如表 2所示,4种方法的预测统计结果与插值精度差异较大. OKLG+TIN、OKBC、IDW、Spline预测的最大值分别为175699.2、115014.3、84752.0、55864.8 mg ·kg-1,预测的最小值分别为82.2、96.0、87.5、102.4 mg ·kg-1,预测的平均值分别为14143.2、11753.4、10857.3、9862.4 mg ·kg-1,可以看出,OKBC、IDW、Spline预测的最大值和平均值远低于实测的最大值和平均值,而预测的最小值均高于实测的最小值,表明该3种方法在插值计算过程中对高值和低值部分都有一定的平滑效应,即高值点部分受其周边低值点的影响,在插值预测后其含量被拉低,低值点部分受周围高值点的影响,预测后的含量被抬高. OKLG+TIN方法预测的最大值、平均值和实测最大值、平均值较为接近,其原因是高值点被拆分后采用TIN方法插值,能够最大程度反映污染的局部特征,拆分掉高值点部分的数据集符合对数克里格插值原理,能够反映出场地的整体污染特征,因此OKLG+TIN方法插值计算结果有效降低了预测过程中的平滑效应,其预测的最小值虽也高于实测最小值,但最小值远低于北京住宅用地标准规定的400 mg ·kg-1,不是修复治理过程重点关注的区域. 从不同方法预测精度的交叉验证结果来看,OKLG+TIN具有最小的ME和RMSE,其次分别是OKBC、IDW和Spline,表明OKLG+TIN具有最高的插值精度,其预测结果能够较为真实地反映场地的实际污染状况. OKBC方法在对原始数据正态变换和逆变换过程中,产生了较大的平滑效应,IDW方法对样点分布位置和样点数量要求较高,样点越多且分布越均匀其预测精度越高,Spline方法一般要求数据集有连续的一阶和二阶导数,受场地部分建筑物和硬化地面等实际情况影响,很难做到高密度和均匀网格布点采样,因此OKBC、IDW和Spline的预测精度都较低.
|
|
表 2 不同插值方法预测统计结果与预测误差 /mg ·kg-1 Table 2 Statistical summary and cross validation error for estimated Pb concentrations of different interpolation methods/mg ·kg-1 |
在对原始数据进行相应的预处理后,使用OKLG+TIN、IDW、Spline、OKBC方法对土壤中Pb含量的分布进行空间插值计算,最终形成的污染物空间分布如图 5所示, 从中可以看出,4种插值方法对污染物空间分布预测的总体趋势相似,但在细部特征上 差异较大. 总体上来看,4种插值方法预测污染较为严重的区域主要分布在厂区的中部和东南部分区域, 分布在厂区中部的主要车间有废铅堆放区、极片生产二车间、一车间等,场地东南区域的车间主要有四车间、五车间等,上述车间在生产以及材料存储过程中涉及到Pb,对土壤中Pb污染的程度较为严重. 从污染预测图的细部变化上来看,OKLG+TIN方法由于对高值点部分采用了TIN方法预测,较好地反映场地局部高污染特征,对拆分出高值点的数据集部分采用OKLG方法预测,符合对数克里格模型的插值原理,能够反映出场地整体的污染趋势,叠加后的污染预测图比较符合场地的实际污染状况. IDW和Spline方法属于确定性插值模型,在计算过程中只依据数据的几何结构特征,未考虑样点的空间信息,对样点要求较高,受样点分布位置和样点数量的影响,其插值结果虽能反映出场地污染的总体趋势,但难以准确反映出污染的局部尤其是高污染区的细部特征. OKBC方法对原始数据做了正态变换处理,符合克里格插值原理,但在数据正态变换以及插值结果的逆变换过程中,对高值点部分产生了很大的平滑效应,同样难以反映出高污染区域的细部特征. 在污染场地风险评估以及修复治理过程中,重点关注的是高污染和高风险区域,受采样样点数量、样点分布以及插值方法适用原理等因素影响,IDW、Spline、OKBC方法预测结果难以反映场地高污染区域的细部变化特征.
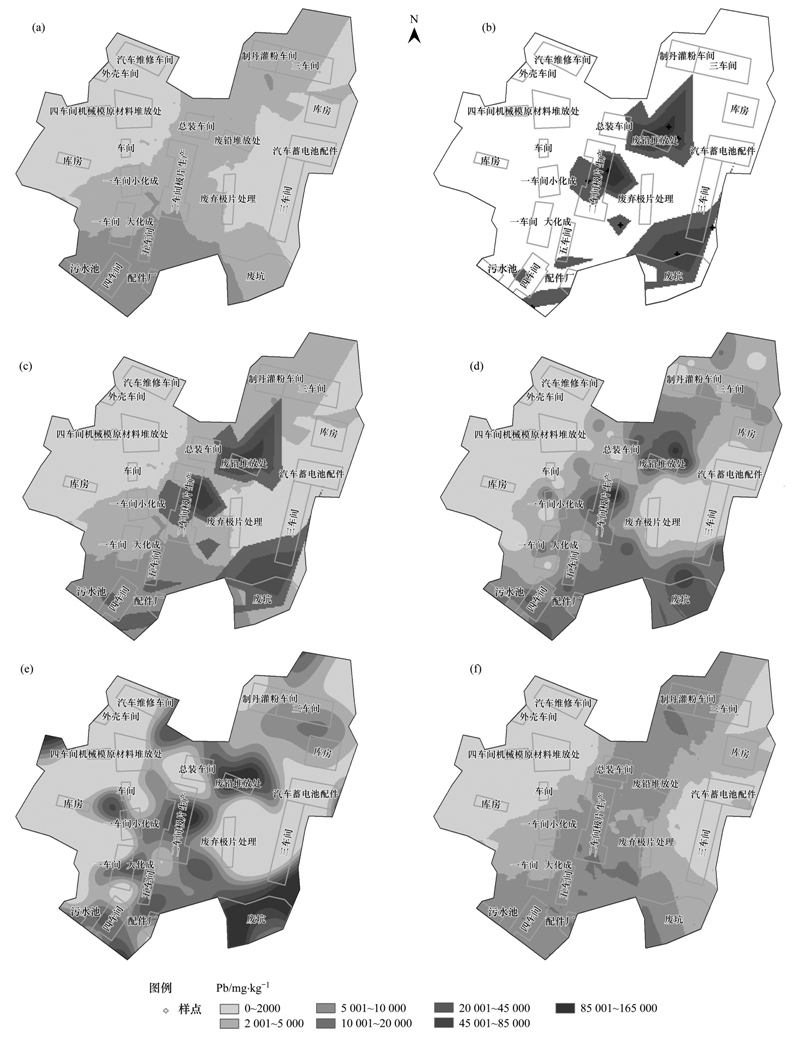 | 图 5 不同插值方法对土壤Pb污染的空间分布预测 Fig. 5 Soil Pb pollution prediction according to different models 图中(a)、(b)、(c)、(d)、(e)、(f)分别表示用OKLG、TIN、OKLG+TIN、IDW、Spline、OKBC方法的插值预测结果 |
参照北京市住宅标准所规定的Pb含量值400 mg ·kg-1,原始样点超标率为58.9%,将预测结果转化为栅格数据进行统计计算,将高于400 mg ·kg-1的区域界定为污染范围,统计结果发现,OKLG+TIN预测的污染范围与样点超标率较为接近,污染超标范围为55.4%,IDW和Spline预测的污染范围高于样点超标率,污染超标范围分别为65.7%和67.9%,OKBC预测的污染范围低于样点超标率,污染超标范围为51.8%. 污染范围界定过大,在修复过程中虽能消除整个场地的污染危害,但会增加修复的投资,影响实际修复工程的开展,污染范围界定过小,降低了修复工程的成本,但不能确保消除整个污染场地的风险. 因此选择合理的插值模型,准确界定污染范围和修复边界,对于指导实际修复工作、消除场地风险和危害具有重要作用.
3 结论
(1)受历史生产过程及人为因素干扰,场地土壤中Pb含量的样点数据集具有严重偏斜特征,统计发现含有异常真实高值点,在局部区域有很强的变异性和污染物空间分布的不连续性. 污染物空间变异特征与污染源对土壤中Pb的累积释放影响较为一致.
(2)不同插值方法预测结果都能反映出场地的总体污染趋势,但现有确定性插值模型和地统计学模型中的IDW、Spline、OKBC方法预测结果不能很好反映场地高污染区域的细部变化,对高污染区域产生很大的平滑效应,预测结果精度较低,难以精确表征场地土壤Pb污染的实际污染特征.
(3)OKLG+TIN对原始数据集拆分后,对高值点部分和其它数据集部分采用分区预测的思路,分别插值计算后再进行叠加处理,可以较好地反映出场地局部区域和整体趋势的污染变化,取得了最高的预测精度,预测结果比较符合场地的实际污染状况,能够较为有效指导污染场地污染范围界定和场地修复方案决策的制定.
| [1] | Forslund J, Samakovlis E, Johansson M V, et al. Does remediation save lives?-On the cost of cleaning up arsenic-contaminated sites in Sweden[J]. Science of the Total Environment, 2010, 408 (16): 3085-3091. |
| [2] | 岳希, 孙体昌, 黄锦楼. 某铅蓄电池厂表土不同粒径中铅分布规律研究[J]. 环境科学, 2013, 34 (9): 3679-3683. |
| [3] | Blake W H, Walsh R P D, Reed J M, et al. Impacts of landscape remediation on the heavy metal pollution dynamics of a lake surrounded by non-ferrous smelter waste[J]. Environmental Pollution, 2007, 148 (1): 268-280. |
| [4] | 骆永明. 中国污染场地修复的研究进展、问题与展望[J]. 环境监测管理与技术, 2011, 23 (3): 1-6. |
| [5] | 郭观林, 王翔, 关亮, 等. 基于特定场地的挥发/半挥发有机化合物(VOC/SVOC)空间分布与修复边界确定[J]. 环境科学学报, 2009, 29 (12): 2597-2605. |
| [6] | 林佳佳, 王维, 居婕, 等. 无锡市锡山区棕(褐)地环境风险评价研究[J]. 中国环境科学, 2013, 33 (4): 748-753. |
| [7] | 姜林, 钟茂生, 朱笑盈, 等. 多证据分析技术在场地重金属污染评价中的应用研究[J]. 环境科学, 2013, 34 (9): 3641-3647. |
| [8] | 刘庚, 郭观林, 南锋, 等. 某大型焦化企业污染场地中多环芳烃空间分布的分异性特征[J]. 环境科学, 2012, 33 (12): 4256-4262. |
| [9] | Franco C, Soares A, Delgado J. Geostatistical modelling of heavy metal contamination in the topsoil of Guadiamar river margins (S Spain) using a stochastic simulation technique[J]. Geoderma, 2006, 136 (3-4): 852-864. |
| [10] | Kamaruddin S A, Sulaiman W N A, Rahman N A, et al. A review of laboratory and numerical simulations of hydrocarbons migration in subsurface environments[J]. Journal of Environmental Science and Technology, 2011, 4 (3): 191-214. |
| [11] | Lark R M. Modelling complex soil properties as contaminated regionalized variables[J]. Geoderma, 2002, 106 (3-4): 173-190. |
| [12] | Rawlins B G, Lark R M, O'Donnell K E, et al. The assessment of point and diffuse metal pollution of soils from an urban geochemical survey of Sheffield, England[J]. Soil Use and Management, 2005, 21 (4): 353-362. |
| [13] | 吴运金, 何跃, 邓绍坡, 等. 污染场地土壤重金属空间异常值识别及其点源效应的分离[J]. 生态与农村环境学报, 2013, 29 (6): 789-795. |
| [14] | Juang K W, Lee D Y. A comparison of three kriging methods using auxiliary variables in heavy-metal contaminated soils[J]. Journal of Environmental Quality, 1998, 27 (2): 355-363. |
| [15] | Wu C F, Wu J P, Luo Y M, et al. Statistical and geoestatistical characterization of heavy metal concentrations in a contaminated area taking into account soil map units[J]. Geoderma, 2008, 144 (1-2): 171-179. |
| [16] | Marchant B P, Saby N P A, Lark R M, et al. Robust analysis of soil properties at the national scale: cadmium content of French soils[J]. European Journal of Soil Science, 2010, 61 (1): 144-152. |
| [17] | Li J, Heap A D. A review of comparative studies of spatial interpolation methods in environmental sciences: Performance and impact factors[J]. Ecological Informatics, 2011, 6 (3-4): 228-241. |
| [18] | Beelen R, Hoek G, Pebesma E, et al. Mapping of background air pollution at a fine spatial scale across the European Union[J]. Science of the Total Environment, 2009, 407 (6): 1852-1867. |
| [19] | Grunwald S. Multi-criteria characterization of recent digital soil mapping and modeling approaches[J]. Geoderma, 2009, 152 (3-4): 195-207. |
| [20] | 郭龙, 张海涛, 陈家赢, 等. 基于协同克里格插值和地理加权回归模型的土壤属性空间预测比较[J]. 土壤学报, 2012, 49 (5): 1037-1042. |
| [21] | D'Or D, Bogaert P. Continuous-Valued map reconstruction with the Bayesian Maximum Entropy[J]. Geoderma, 2003, 112 (3-4): 169-178. |
| [22] | Wu J, Norvell W A, Welch R M. Kriging on highly skewed data for DTPA-extractable soil Zn with auxiliary information for pH and organic carbon[J]. Geoderma, 2006, 134 (1-2): 187-199. |
| [23] | Juang K W, Liao W J, Liu T L, et al. Additional sampling based on regulation threshold and kriging variance to reduce the probability of false delineation in a contaminated site[J]. Science of the Total Environment, 2008, 389 (1): 20-28. |
| [24] | 张贝, 李卫东, 杨勇, 等. 贝叶斯最大熵地统计学方法及其在土壤和环境科学上的应用[J]. 土壤学报, 2011, 48 (4): 831-839. |
| [25] | http://www.epa.gov/osw/hazard/testmethods/sw846/pdfs/6010c.pdf. |
| [26] | Robinson T P, Metternicht G. Testing the performance of spatial interpolation techniques for mapping soil properties[J]. Computers and Electronics in Agriculture, 2006, 50 (2): 97-108. |
 2014, Vol. 35
2014, Vol. 35


