2. 昆明理工大学国土资源工程学院, 昆明 650093;
3. 宁夏大学地理科学与规划学院, 银川 750021
2. Faculty of Land Resources Engineering, Kunming University of Science and Technology, Kunming 650093, China;
3. School of Geography and Planning, Ningxia University, Yinchuan 750021, China
土壤是人类赖以生存的自然资源, 土壤质量直接关系到耕地保护和粮食安全[1~3]. 准确掌握土壤信息, 根据土壤质量科学进行农业生产布局, 是提升粮食生产能力的关键. 土壤有机质(soil organic matter, SOM)是构成土壤的核心物质, 研究查明区域SOM含量及空间分布, 对保护耕地、优化种植结构和调节施肥措施具有指导作用.
近年来, 学者们通过不同方法对全国不同尺度的SOM含量及空间分布特征进行了大量研究. 王绍强等[4]利用第二次全国土壤普查典型土壤剖面数据估算和分析了全国土壤有机碳库储量及其空间分布特征, 黄耀等[5]对20年来(1994~2003年)中国大陆农田表土中有机碳含量的变化进行了分析, 结果表明53%~59%的农田土壤有机碳含量呈增长趋势, 华东和华北地区增长最为明显. 同样, 杨帆等[6]通过对第二次全国土壤普查数据与2005~2014年测土配方施肥项目数据对比分析, 表明近30年来我国农田耕作层SOM含量总体呈上升趋势, 较全国第二次土壤普查时期提高了24.49%. 张维理等[7]分析了我国7个代表性地区30年来SOM时空演变趋势情况, 表明各地区SOM含量空间分布总体规律相似, 同时也指出了在全国尺度上获取精细土壤质量数据需要进行大样本量的地面调查和采样. 在预测方法上, 机器学习法逐步应用于全国尺度的SOM含量预测[8~11]. 相对于全国范围, 在省级尺度, 预测和分析空间分布变化趋势广泛应用了地统计插值方法[12~15]、经典统计学方法[16, 17]和机器学习方法[18]. 在县域尺度, 与SOM相关的环境因子作为辅助变量被纳入预测, 有研究表明在不同区域SOM的空间分布与采样尺度[19]、地形和地貌密切相关, SOM存在较强的空间自相关性[20], 地统计插值法与土壤类型法在估算土壤有机碳储量方面具有明显的差异[21], 不同类型土壤的有机质含量差异明显[22], 同时, 人类活动及耕作和土地利用也是重要的影响因素[23]. 地统计与环境因子和邻近信息结合可获得更好的预测结果[24], 确定性插值法在更小尺度(乡镇)上具有可行性[25].
上述研究大多是利用了自然环境因子作为辅助变量来预测SOM含量, 人为因子考虑较少, 但土壤属性具有复杂性, 辅助变量与土壤属性是非线性关系, 尺度与地域不同, 各因子的筛选也需要结合实际情况开展[26, 27]. 预测方法上, 神经网络、随机森林等机器学习法应用于SOM空间分布预测迅速发展[28~30], 但结合群智能算法的较少.
BP(back propagation, BP)神经网络采用反向传播算法, 能学习和存贮输入-输出模式映射关系, 无需事前揭示描述这种映射关系的数学方程, 在预测土壤有机质空间分布方面被证明有很大优势[31, 32], 但传统BP神经网络存在收敛速度慢、易陷入局部最优等问题, 因此需要对BP神经网络进行优化. 近年来, 群智能优化算法发展迅速, 这些算法具有较强的鲁棒性和搜索能力, 在许多领域得到了广泛地研究和应用. 麻雀搜索算法是一种较新的智能优化算法, 具有较高的收敛性能与全局搜索能力. 卫宁平原作为黄河流域宁夏段粮食主产区和人口聚集区, SOM与自然和人类活动紧密相关, 群智能算法优化BP神经网络预测SOM含量在研究区未见相关研究.
鉴于此, 本文以卫宁平原为研究区, 引入与县域尺度SOM紧密相关的自然与人类活动等辅助变量, 选择经典统计学方法、确定性插值方法、地统计插值方法和群智能算法优化的机器学习方法, 通过预测精度的对比分析, 探索县域尺度预测SOM含量的最佳方法.
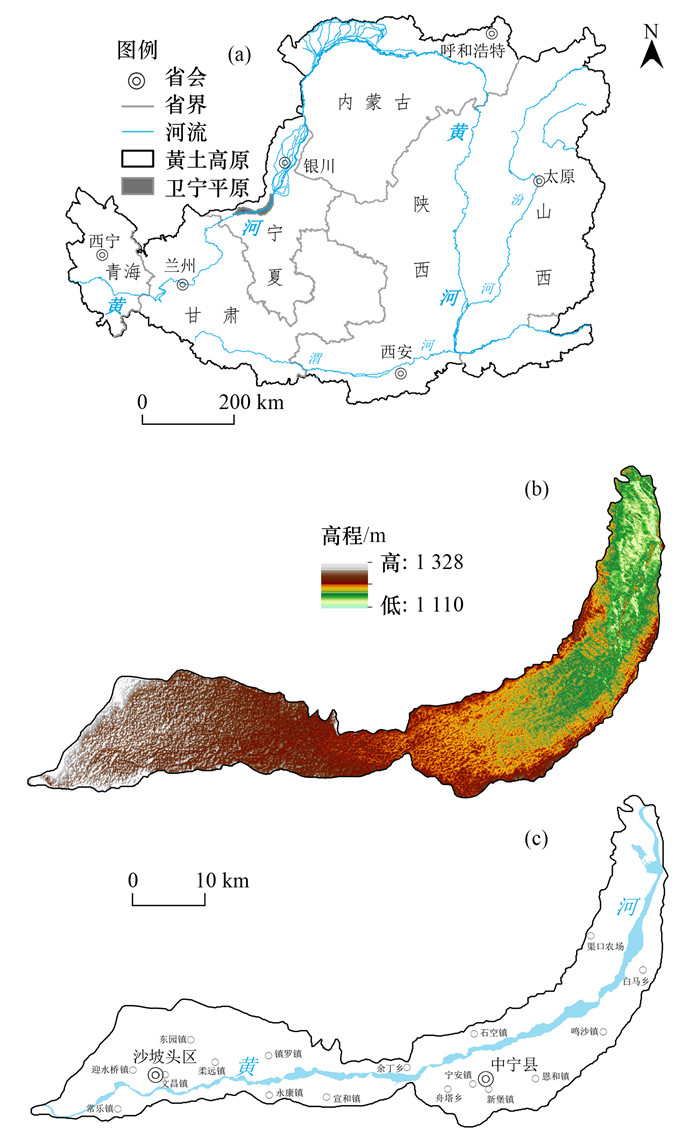
1 材料与方法 1.1 研究区概况卫宁平原地处黄土高原, 位于河套灌区的西套, 行政区划为宁夏回族自治区沙坡头区、中宁县和青铜峡市所辖(105°00′~106°00′E, 37°20′~37°50′N), 是历史悠久的黄河自流灌区, 总面积1 086 km2, 其中耕地面积480 km2(图 1). 卫宁平原为典型北温带大陆性季风气候, 多年平均气温为10.54℃, 降水稀少, 蒸发强烈, 主要河流为黄河及支流清水河和红柳沟. 卫宁平原为新生代断陷盆地, 研究区内发育黄河三级阶地, 依次为黄河两岸分布的冲积层, 冲积阶地后缘局部分布的冲洪积层、以及风积层. 地形地貌主要以黄河冲积与洪积平原为主. 研究区成土母质多为全新统河流冲洪积物, 其次为更新统洪积层, 全新统风积层最少. 根据第三次全国国土调查数据成果统计, 研究区主要地类为耕地(水田、水浇地和旱地), 主要分布在黄河两侧平原区域内. 主要种植水稻、小麦、枸杞、蔬菜、红枣和硒砂瓜等特色农产品, 是供港蔬菜基地和国家道地中药材枸杞的发源地和正宗原产地.
|
(a)基于2011年国家基础地理信息系统平台(http://nfgis.nsdi.gov.cn)全国1∶400万基础地理数据制作 图 1 研究区地理位置及数字高程模型 Fig. 1 Location and digital elevation model of study area |
土壤推理制图需要根据特定制图要求选择相应的土壤-环境关系表达模型, 采样和推理制图是相互联系的过程. 采样造成的误差远超样品处理与实验数据分析[33], 一般而言, 样点密度和代表性决定了制图精度[34]. 在布设采样点时, 权衡精度、成本和可达性等, 以高分二号遥感影像为底图, 规则公里网格为基础预设土壤采样点, 再综合考虑第三次全国国土调查土地利用现状图斑, 对样点位置进行优化调整, 确保采样点主要在农用地. 在2020~2021年分两批完成野外采集, 土壤样点用手持GPS记录坐标, 在定位中心周围100 m范围内随机选择5个分样点进行充分混合, 采样深度为0~20 cm, 共采集土壤样品1 690个.
土壤样品经风干、研磨和过20目筛等预处理后送实验室测定. 利用重铬酸钾外加热法测定SOM含量, 称取0.500 0 g样品于三角烧杯中, 加入5 mL 0.8 mol·L-1的重铬酸钾标准溶液、5 mL浓硫酸, 摇匀并于电热板上消解, 冷却后加入邻菲罗啉指示剂, 硫酸亚铁滴定. 利用离子选择电极法测定pH, 称取10.0 g样品, 加无二氧化碳蒸馏水浸溶, 用pH计测定.
1.2.2 辅助数据来源与处理土壤数字制图引入定量辅助因子可以提高预测精度[35]. 地形因子能较好反映土壤发生和发育[36], 经常用于土壤性质空间分布预测[37]. 已有研究表明在比较新形成的冲积单元上, 地形与土壤属性的关系远比其他景观单元密切, 丘陵区地形因素对土壤性质空间分布影响明显, 县域尺度土壤类型较土地利用类型和地貌类型对有机质影响更大[38]. 区域植被覆盖信息也与当地土壤有机质密切相关, 常用于表征土壤性质[39]. 各级尺度中, 土壤类型信息都十分重要[40]. pH被证明对SOM有着比较复杂的影响[41]. 已有研究表明在较小空间范围, 一般不考虑气候因素[42], 所以本研究未考虑气象因素. 综上, 本文选择了地理坐标、地形、土壤类型、pH和人口等10类代理变量, 土壤类型用于反映自然资源本底的差异;经纬度代表空间上的差异;高程、坡度、坡向与植被代表自然影响因素;土地利用与人口代表人类活动影响因素. 地理坐标在采样时实测;pH由土壤样品测定;植被因子采用归一化植被指数(normalized difference vegetation index, NDVI), 详见表 1.
|
|
表 1 数据类型与来源1) Table 1 Data type and source |
经纬度由手持GPS实测(水平精度5 m);数字高程模型采用ASTGTM2数据(分辨率30 m);坡度坡向数据由数字高程模型在GIS软件中计算得到;植被指数采用MODIS遥感数据产品的NDVI(2021年8月, 分辨率250 m);pH为实测然后用普通克里格插值得到栅格数据(分辨率30 m);人口数据采用人口密度(分辨率30″);土壤类型分为灌淤土、灰钙土、潮土、新积土、盐土和风沙土等6个土类, 由1∶25万宁夏土壤图数字化得到[43];土地利用采用第三次全国国土调查成果, 分为耕地、草地、园地和林地这4类. 对各类数据进行质量检查和预处理后, 重采样至30 m分辨率. 在GIS软件中将各辅助变量栅格数据值提取到采样点上, 生成实验数据.
1.3 研究方法 1.3.1 虚拟变量的引入土壤类型、土地利用类型与土壤表层有机质分布密切相关, 在预测中将这些因素纳入自变量考虑. 但土壤类型、土地利用类型属于类别变量, 获取的属性只是类型的划分, 需将其转换为虚拟变量才能进行回归分析. 虚拟变量(dummy variables)又称哑变量, 在回归分析时, 更能全面刻画因变量的影响因子, 能够提高回归模型的精度[44, 45].
虚拟变量不代表大小, 如果变量可划分为n类, 在回归分析时为避免共线性, 当回归模型包含截距时, 则定义n - 1个虚拟变量, 赋值如下:
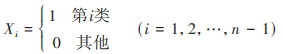
|
(1) |
式中, Xi为分类变量, i表示分类变量下的不同属性. 本研究选择土壤类型和土地利用类型为虚拟变量. 土壤类型选取潮土、风沙土、灌淤土、灰钙土、新积土和盐土这6类, 以盐土为参考类型;土地利用类型选取耕地、草地、园地和林地这4类, 以林地为参考类型.
1.3.2 麻雀搜索算法BP神经网络是一种按误差逆传播算法训练的多层前馈网络[46]. BP神经网络虽然是人工神经网络中应用最广泛的算法, 但也存在着一些缺陷, 比如学习收敛速度慢, 不能保证收敛到全局最小点、网络结构不易确定等. 网络的初始连接权值和阈值的选择对网络训练的影响很大, 但又无法准确获得, 针对这些特点可以采用智能优化算法对神经网络进行优化. 近年来群智能优化算法发展迅速, 在其他领域成为优化BP神经网络研究的热点.
麻雀搜索算法是依据麻雀觅食、逃避捕食者的行为提出的一种新型群智能优化算法[47, 48], 该算法主要依据麻雀种群的行为解决目标函数的最优问题. 麻雀种群在觅食时一部分负责提供觅食区域和方向, 其余麻雀进食, 如果意识到危险, 部分麻雀会发出警报, 整个种群会立即做出反应, 按照分工将其分为发现者、追随者和警戒者.
发现者位置更新:
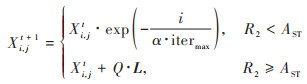
|
(2) |
式中, Xi, j为麻雀个体所在位置, t为迭代次数;α为随机数且α∈(0, 1], R为麻雀个体遇到危险时发出的预警值且R∈(0, 1];ST为发生转移的阈值且ST∈(0, 1];Q为随机数;L为一个一行多维的全一矩阵.
追随者位置更新:

|
(3) |
式中, Xworst为麻雀个体适应度最差位置, Xb为发现者所在最佳位置;A表示一个一行多维矩阵, 且每个元素随机赋值为-1或1, 且A+ = AT(AAT)-1.
警戒者位置更新:
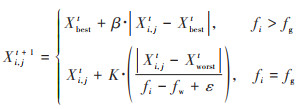
|
(4) |
式中, Xbest为当前全局最佳位置, β为步长控制参数;fi为当前第i个麻雀的适应度;fg为当前全局最佳适应度;fw为当前全局最差适应度;ε为常数, K为随机数.
麻雀搜索算法2020年由国内学者首次所提出[47, 48], 具有收敛速度快、局部搜索能力强的优势, 但全局搜索能力较弱, 因此在县域尺度预测土壤属性需要进一步改进麻雀搜索算法(optimized sparrow search algorithm, OSSA), 然后对BP神经网络的阈值、权值和偏置进行寻优处理, 进一步提高预测精度.
1.3.3 麻雀搜索算法改进原始的麻雀搜索算法在初始化种群时, 是随机产生的, 这会导致麻雀种群多样性不佳, 造成算法的全局搜索能力下降, 因此引入混沌映射函数对原算法进行改进[49].
(1)混沌映射
混沌映射被用于生成混沌序列, 是一种随机性序列, 在优化领域, 混沌映射可以用于替代伪随机数生成器, 生成0到1之间的混沌数. 本文采用Cubic映射来初始化麻雀搜索算法参数.
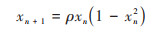
|
(5) |
式中, ρ为控制参数, Cubic映射序列值在(0, 1)之间, 并且当x0 = 0.3, ρ = 2.59时生成的混沌变量具有更好的遍历性.
(2)萤火虫扰动
萤火虫算法是根据萤火虫的闪烁行为而提出的一种元启发式算法[50]. 在萤火虫优化算法中, 萤火虫的位置表示优化问题的可行解, 亮度对应萤火虫位置的适应度值. 萤火虫不断向更亮萤火虫移动, 以搜索更优位置, 直至搜索到优化问题的最优解, 完成寻优.
萤火虫的相对荧光亮度:
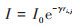
|
(6) |
式中, I0为最亮萤火虫的亮度, 即自身(r = 0处)荧光亮度, 目标函数组越优, 自身亮度越高;γ为光吸收系数, 因为荧光会随着距离的增加和传播媒介的吸收逐渐减弱, 所以设置光强吸收系数以体现此特性, 可设置为常数;ri,j为萤火虫i与j之间的距离.
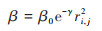
|
(7) |
式中, β0为最大吸引度, 即光源处(r = 0处)的吸引度.
最优目标迭代:
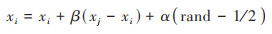
|
(8) |
式中, xi和xj分别为i和j两个萤火虫的空间位置, α为步长因子, rand为[0, 1]上服从均匀分布的随机因子.
1.3.4 模型构建选用经典统计学方法中多元逐步回归模型(multiple linear regression analysis, MLRA);确定性插值方法中反距离权重(inverse distance weighting, IDW)、径向基函数法(radial basis functions, RBF);地统计插值方法中普通克里格(ordinary Kriging, OK)以及普通最小二乘法(ordinary least squares, OLS)结合普通克里格插值(OLS-OK);机器学习采用未优化的BPNN作为对照方法.
OK法以半方差函数分析为基础, 构建最佳模型及相关参数进行插值. OLS-OK法首先采用普通最小二乘法进行土壤表层有机质与环境因子的回归预测, 研究表明回归预测结果残差具有空间自相关性, 再用普通克里格对回归预测结果残差进行插值, 最后将回归预测结果和普通克里格法预测残差趋势面相加, 得到最终结果.
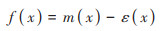
|
(9) |
式中, f(x)为点x处的土壤有机质预测值;m(x)为在x处回归得到的趋势项;ε(x)为由普通克里格在x处的残差项.
为了便于对比预测精度, 机器学习法均采用表 1中的10类数据共计18个因子参与模型构建. BP神经网络将1.2.2节中自然环境、人类活动因子归一化后作为网络输入, 以归一化后的实测SOM含量作为网络输出, 在Matlab R2021b中构建和训练神经网络模型, 训练函数选trainlm, 隐含层激活函数为logsig, 输出层激活函数为purelin, 预测输入数据为18维, 输出数据为1维. 网络模型训练次数为1 000次, 学习率为0.01, 最大迭代次数为100, 通过反复试算选取均方根误差最小时的隐含层节点为模型的最佳隐含层节点数, 最终确定为12.
OSSA-BPNN法首先采样Cubic映射初始化种群, 增强全局搜索能力, 再用萤火虫扰动优化策略对最优解位置进行扰动, 避免陷入局部最优, 然后把最优初始化阈值权值赋予BP神经网络, 为便于对比, BP神经网络其他参数与前文设置一致, 最后将预测值在GIS中可视化.
1.3.5 精度评价在GIS软件中随机从1 690个土壤样点中提取约20%(342个)样点作为验证点, 为使验证点更具有代表性, 在随机提取时考虑空间分布情况, 设置相互间距大于1 km, 其余1 348个样点作为建模点, 通过比较样点土壤表层有机质预测值与实测值的平均绝对误差(mean absolute error, MAE)、平均相对误差(mean relative error, MRE)、均方根误差(root mean square error, RMSE)、相关系数(r)和林氏一致性相关系数(concordance correlation coefficient, CCC)进行预测精度评价. 计算公式如下:
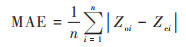
|
(10) |
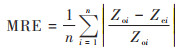
|
(11) |
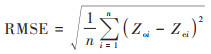
|
(12) |
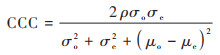
|
(13) |
式中, Zoi为第i个点的实测值(g·kg-1);Zei为预测值(g·kg-1);n为用于检验的点的数目. σo为测量值方差, σe为预测值方差, μo为平均测量值(g·kg-1), μe为平均预测值(g·kg-1), ρ为Pearson相关系数. 绝对差值越小, 相关性越强, CCC值也越大, 因此该值越接近1, 则算法的表现越好. MAE反映估计值的实测误差范围, 定量给出误差的大小, RMSE主要反映样点数据的估值和极值效应, CCC结合了MSE和Pearson相关系数的特点, 提供了一种可以同时度量相关性和绝对插值的指标.
统计采用SPSS 23软件探索SOM含量的空间分布情况及其与各影响因素间的相关性和异质性关系, 使用Pearson相关系数来计算辅助变量之间的关系, 使用GS+9.0分析SOM的空间自相关及Moran's I指数.
2 结果与分析 2.1 样本描述性统计分析统计结果表明(表 2), 1 690个采样点ω(SOM)的平均值为14.34 g·kg-1, 最小值为0.60 g·kg-1, 最大值为35.70 g·kg-1, 变异系数为34.81%, 为中等程度的变异性. SOM含量较高的样点主要位于常乐镇、中宁县城周边, 较低的区域主要分布于新堡镇以南, 不同土壤类型对应的SOM差异较大, 灌淤土、灰钙土、新积土、风沙土、潮土和盐土的ω(SOM)的平均值分别为15.51、8.79、8.33、6.58、14.48和14.48 g·kg-1.
|
|
表 2 研究区土壤有机质含量描述性统计特征 Table 2 Descriptive statistic characteristics of SOM content |
从数据的分布形态看, 采样点数据偏度为-0.18, 峰度为3.34, 经过Kolmogorov-Smirnov(K-S)检验, P < 0.05. K-S检验在样本量较大的时候, 检验结果又会太过敏感, 只要数据稍有偏离, 则P < 0.05, 检验结果倾向于拒绝原假设, 认为数据不服从正态分布. 所以, 如果样本量足够多, 即使检验结果P < 0.05, 数据总体也可能是服从正态分布的. 通过参考Q-Q图, 发现数据接近于正态分布. 样本点的全域Moran's I指数为0.39, 其SOM含量存在空间自相关.
2.2 半方差函数分析训练集SOM半方差函数分析结果显示(表 3), 研究区最优模型为指数模型, 拟合系数为0.998, 块金值与基台值分别为7.810和23.450, 块金效应66.7%, 小于75%, 表明研究区SOM具有中等程度的空间相关性, 变程为7 647 m, 空间自相关范围较大.
|
|
表 3 土壤有机质半方差函数模型及参数 Table 3 Parameters of the semi-variogram models for SOM |
2.3 多元逐步回归
多元逐步回归过程如表 4所示, 标准化系数是拟合方程的实际参数, 其大小是自变量对因变量重要程度的体现. 在显著性0.05的检验水准下, 坡度、坡向和土地利用虚拟变量的回归系数检验P值均大于0.05, 说明坡度大小、坡向不同和土地利用方式不同对SOM不存在显著差异. 因此剔除坡度、坡向和土地利用等8个因子, 剔除后进行逐步回归, 检验最大方差膨胀系数(variance inflation factor, VIF)均小于7.5(VIF < 7.5), 说明变量之间不存在共线性. 最终回归模型为:
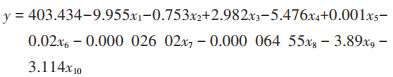
|
|
|
表 4 多元逐步回归过程1) Table 4 Process of multiple stepwise regression |
式中, y为有机质含量(g·kg-1);x1为pH值, x2为潮土, x3为NDVI, x4为风沙土, x5为人口, x6为高程, x7为经度, x8为纬度, x9为灰钙土, x10为新积土. 方差分析其残差平方和为30 974.109, F值为312.391, P < 0.001, 表明回归方程显著.
2.4 预测结果使用7种方法对SOM含量进行预测. 由表 5可知, 这7种方法预测平均值均小于实测值, 除RBF外, 其他方法预测的SOM的最大值均≤35.70g·kg-1, 与训练集相比, 高值区有一定的压缩. IDW和RBF模型得到的高值、低值预测较为接近, 对比表 2发现, IDW、RBF、OK和OLS-OK模型预测平均值较为接近, 而MLRA、BPNN和OSSA-BPNN方法预测结果平均值相近. 表 5中OLS-OK预测最小值出现了负值(-0.31), 具有明显的错误, 分析发现OLS-OK法的残差在插值中具有不确定性, 导致负值的出现, 该负值区域位于研究区西南角采样点稀疏的几个栅格单元.
|
|
表 5 研究区土壤有机质含量预测结果统计特征/g·kg-1 Table 5 Statistical characteristics of soil organic matter content predicated result/g·kg-1 |
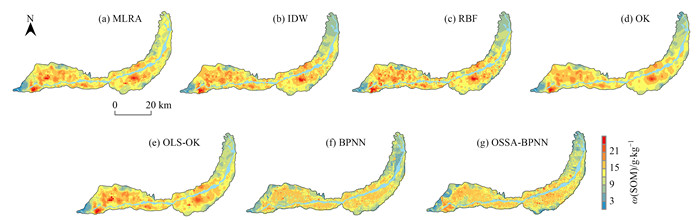
不同模型预测卫宁平原SOM空间分布如图 2所示, 这7种方法预测趋势基本一致, SOM空间分布特征为东北部、西南地区含量低, 中间黄河左右岸含量高, 地势平缓的黄河阶地相对含量高. 研究区SOM含量高值区主要分布在沙坡头区的常乐镇、柔远镇和宣和镇, 中宁县的鸣沙镇、恩和镇北部与石空镇东部, 低值区主要分布在迎水桥镇以西、东园镇和镇罗镇以北, 白马乡和渠口农场以北. 高值区有七星渠、美利渠等渠系分布, 高值可能与引水引沙及泥沙冲淤有关[51, 52], 农田淤积物以粉粒为多, 土壤质地随灌溉水淤积加重, 有机质与矿质养分含量富集[53]. 低值区主要在风沙土区和湿地.
|
图 2 不同模型预测SOM含量空间分布 Fig. 2 Spatial distribution of predicted values of SOM content in different models |
利用验证集342个点位数据, 将7种预测方法的精度指标进行对比, 结果见表 6. 总体来看, MLRA的各项精度指标最差, 说明利用多元逐步回归模型进行SOM预测的精确度最低, IDW与RBF确定性内插法预测精度稍低于OK地统计法, 但相差不大. OLS-OK法预测精度较前4种方法高, 但低于OSSA-BPNN, 说明将残差进行克里格插值, 用于消除误差的方法可提高预测精度, 这与文献[14, 20, 31, 32]的研究结论一致. 不同预测模型RMSE和MAE排序结果都依次为:MLRA>RBF>IDW>OK>BPNN>OLS-OK>OSSA-BPNN;MRE排序依次为:MLRA>IDW>OK>RBF>OLS-OK>BPNN>OSSA-BPNN;进一步说明这7种预测方法中OSSA-BPNN预测精度最高. 从相关系数r来看, MLRA法的相关性系数最低、OSSA-BPNN法最高, 说明通过改进麻雀搜索算法进行优化BP神经网络方法得到的预测值与样本实测值之间的相关性最高.
|
|
表 6 预测模型精度指标统计特征 Table 6 Statistic characteristics of precision indexes of prediction model |
3 讨论 3.1 预测模型精度及影响因素
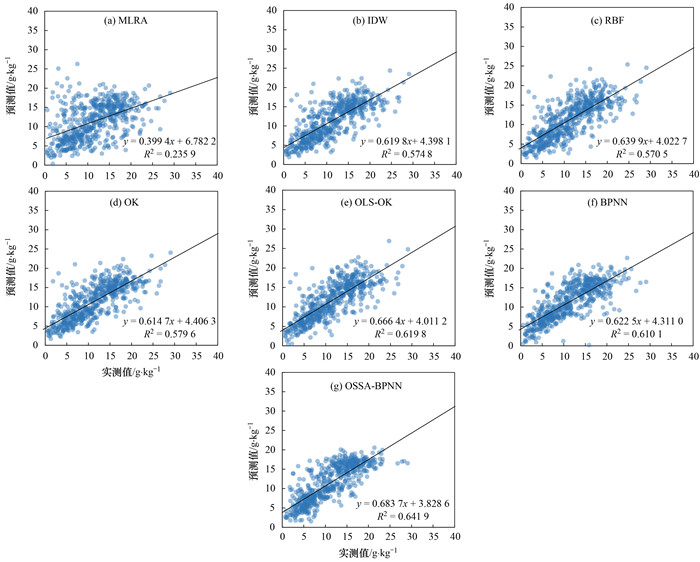
为进一步研究不同方法预测精度, 对SOM实测值和预测值进行线性拟合, 结果如图 3所示. 从中可知, 除MLRA法SOM实测值和预测值之间R2低于0.5外, 其余方法R2均高于0.5, OLS-OK、BPNN和OSSA-BPNN均在0.6以上. MLRA拟合效果最差, IDW、RBF、OK拟合效果接近, OSSA-BPNN拟合效果最好. OLS-OK效果优于OK, 说明引入回归预测结果残差面计算可以提高精度, OSSA-BPNN效果优于BP, 说明优化提高了精度. 以MLRA为参照, RBF、IDW、OK、BPNN、OLS-OK和OSSA-BPNN的预测精度分别提高了29.29%、30.04%、30.60%、32.28%、33.58%和37.13%. MLRA法得到的拟合点分布最为离散, 而机器学习的方法得到的拟合点分布的离散程度最低, 趋于集中, 该方法预测能力得到有效提升.
|
图 3 不同模型预测值和实测值回归分析 Fig. 3 Linear regression analysis of predicted values and measured values of different prediction methods |
从面积来讲本研究为县域尺度, 获取的辅助变量数据来源不一、精度不一, 如DEM分辨率为30 m, 而NDVI为250 m, 在统一空间分辨率时栅格重采样可能对辅助变量数据精度造成影响. pH数据是实地采样化验、用普通克里格法进行插值得到, 可能造成误差的传递叠加. 已有研究表明, 宁夏SOM随土壤质地由轻而重地富集[54], 在县域尺度, 土壤全氮含量与SOM密切相关[55]. SOM在黄河流域与人类活动密切相关, 代表人类活动的协变量诸如耕作制度、施肥方式, 代表自然的土壤质地、土壤理化性质和地下水埋深等因子, 因数据获取受限未能全部纳入模型预测, 一定程度上影响了预测精度.
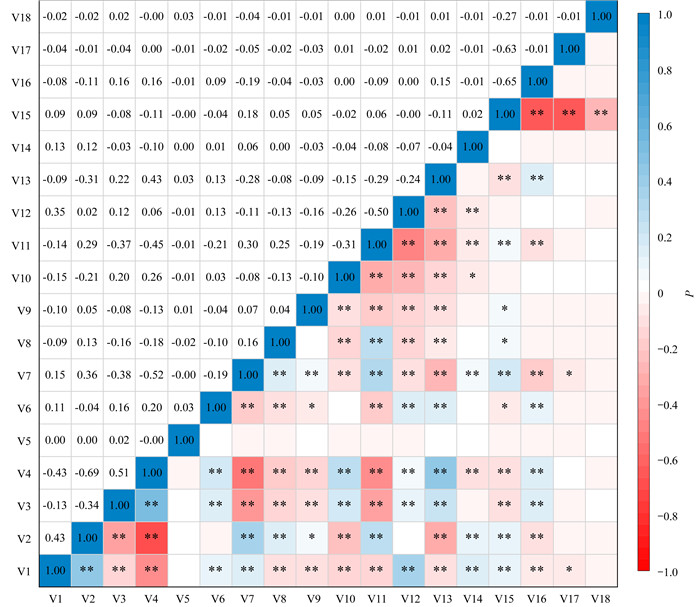
3.2 辅助变量相关性分析由图 4可知, 预测土壤有机质辅助变量中高程与纬度、NDVI呈现中等线性相关, 均为负相关, 与pH呈现中等程度的正相关. 已有研究表明高程与SOM呈负相关[20, 22], 间接说明研究区表层SOM与纬度和NDVI呈正相关;土壤pH值越大、海拔越高、坡度越大, SOM含量越低. 坡向与其他变量几乎无相关性, 人口与灌淤土呈正相关, 表明人类活动比如施肥、灌溉和耕作方式影响着当地SOM含量高低. 土地利用中耕地、草地和园地呈现中等线性相关, 土壤类型因子相互间线性关系很小. 整体而言, 18个自变量相互无强相关性, 说明因子在选取上是合理的, 在2.3节中为避免多重共线性经筛选保留了10个自变量, 但多元逐步回归模型预测精度仍是最低的, 表明经典统计学方法在预测SOM含量中的局限性.
|
V1.经度, V2.纬度, V3.pH, V4.高程, V5.坡向, V6.坡度, V7.NDVI, V8.人口, V9.潮土, V10.风沙土, V11.灌淤土, V12.灰钙土, V13.新积土, V14.盐土, V15.耕地, V16.草地, V17.园地, V18.林地;P表示Pearson相关性系数, *表示P < 0.05, **表示P < 0.01 图 4 辅助变量相关性分析 Fig. 4 Pearson's correlation analysis of auxiliary variables |
多元逐步回归过程中, 土地利用方式对SOM含量不存在显著差异, 这与张宏帅等[32]研究结果不同, 主要原因可能是本研究区在平原且地处黄灌区, 而文献[32]研究区地貌以山地、丘陵为主, 说明地形地貌对SOM的重要性. OK是SOM预测最常用的方法, 充分考虑了区域SOM含量的空间变异, 但插值结果不够精细, 图斑较大, 不能刻画细部特征. 本研究采样点密度为1.72个·km-2, 基本达到合理样本密度1.85个·km-2[56], 因此可较稳健模拟SOM空间结构特征. 由于本研究在白马乡以北和常乐镇以西样点较少, 内插法与统计学法插值在该区域视觉上出现了条块状.
OLS-OK法在回归预测结果残差进行插值过程中, 可能出现ε(x) > m(x)的情况[见公式(9)], 从而出现结果为负值的不正确预测(表 5), 经分析负值区域采样点较为稀疏, 因此采用OLS-OK法一定要注意采样点的空间分布与密度, 避免出现残差大于回归预测结果的现象. 总体而言, OLS-OK法在采样点密度高的情况下整体预测精度高, 但外推能力弱. 而机器学习的方法逐像元计算, 在采样点稀少的研究区东北部, 主要是青铜峡库区湿地, 为SOM含量的低值区, 但MLRA预测明显偏高, RBF、IDW、OK和OLS-OK法在形状上与实地不符, 未能预测出白马乡以北的广武一带零星分布的耕地SOM. 相比而言BPNN和OSSA-BPNN能够刻画SOM与外界因素的非线性关系, 更切合实际, 在视觉上还原了不同地类轮廓, 尤其在数据稀少区域有很大的预测优势, 这与文献[29]研究结论相同. 但模型需要反复训练, 调节优化参数才能取得好的预测效果.
4 结论(1)卫宁平原ω(SOM)的平均值为14.34 g·kg-1, 范围在0.60 ~ 35.70 g·kg-1之间, 变异系数为34.81%, 空间分布总体为东北部、西南地区含量低, 中间黄河左右岸含量高, 地势平缓的黄河阶地含量相对高.
(2)经典统计学、确定性内插、地统计学、机器学习等方法预测结果趋势基本一致. 以MLRA为参照, RBF、IDW、OK、BPNN、OLS-OK和OSSA-BPNN的预测精度分别提高了29.29%、30.04%、30.60%、32.28%、33.58%和37.13%. 经典统计学预测效果最差, 地统计学和普通最小二乘法结合的预测方法可以取得较高的预测精度, 但残差在插值过程中的不确定性不可忽视.
(3)机器学习在点位稀疏的区域预测更具优势, 其结果更加精细, 更贴近真实环境现状. 改进麻雀搜索算法优化BP神经网络具有更优的收敛精度, 避免了陷入局部最优的现象, 防止了数据过拟合, 预测效果更好, 是本文所研究县域尺度预测SOM含量的最佳方法. 本研究为黄河流域典型灌区土壤属性空间分布的准确预测提供了较为可行的方法.
| [1] | 徐建明. 土壤学[M]. ((第四版)). 北京: 中国农业出版社, 2019. |
| [2] |
刘旭. 新时期我国粮食安全战略研究的思考[J]. 中国农业科技导报, 2013, 15(1): 1-6. Liu X. Thoughts of China's food security strategy in the new era[J]. Journal of Agricultural Science and Technology, 2013, 15(1): 1-6. |
| [3] |
周立波. 中国土壤质量研究发展脉络解析[J]. 中国水土保持科学, 2018, 16(3): 142-152. Zhou L B. Historical venation of researches on soil quality in China[J]. Science of Soil and Water Conservation, 2018, 16(3): 142-152. |
| [4] |
王绍强, 周成虎, 李克让, 等. 中国土壤有机碳库及空间分布特征分析[J]. 地理学报, 2000, 55(5): 533-544. Wang S Q, Zhou C H, Li K R, et al. Analysis on spatial distribution characteristics of soil organic carbon reservoir in China[J]. Acta Geographica Sinica, 2000, 55(5): 533-544. |
| [5] | 黄耀, 孙文娟. 近20年来中国大陆农田表土有机碳含量的变化趋势[J]. 科学通报, 2006, 51(7): 750-763. DOI:10.3321/j.issn:0023-074X.2006.07.002 |
| [6] |
杨帆, 徐洋, 崔勇, 等. 近30年中国农田耕层土壤有机质含量变化[J]. 土壤学报, 2017, 54(5): 1047-1056. Yang F, Xu Y, Cui Y, et al. Variation of soil organic matter content in croplands of China over the last three decades[J]. Acta Pedologica Sinica, 2017, 54(5): 1047-1056. |
| [7] |
张维理, 傅伯杰, 徐爱国, 等. 中国土壤调查结果的地统计特征[J]. 中国农业科学, 2022, 55(13): 2572-2583. Zhang W L, Fu B J, Xu A G, et al. Geostatistical characteristics of soil data from national soil survey works in China[J]. Scientia Agricultura Sinica, 2022, 55(13): 2572-2583. |
| [8] |
李启权, 王昌全, 岳天祥, 等. 基于神经网络模型的中国表层土壤有机质空间分布模拟方法[J]. 地球科学进展, 2012, 27(2): 175-184. Li Q Q, Wang C Q, Yue T X, et al. Method for spatial simulation of topsoil organic matter in China based on a neural network model[J]. Advances in Earth Science, 2012, 27(2): 175-184. |
| [9] | Liang Z Z, Chen S C, Yang Y Y, et al. National digital soil map of organic matter in topsoil and its associated uncertainty in 1980's China[J]. Geoderma, 2019, 335: 47-56. DOI:10.1016/j.geoderma.2018.08.011 |
| [10] | Liu F, Wu H Y, Zhao Y G, et al. Mapping high resolution national soil information grids of China[J]. Science Bulletin, 2022, 67(3): 328-340. DOI:10.1016/j.scib.2021.10.013 |
| [11] | Zhang Z P, Ding J L, Zhu C M, et al. Exploring the inter-decadal variability of soil organic carbon in China[J]. CATENA, 2023, 230. DOI:10.1016/j.catena.2023.107242 |
| [12] |
赵永存, 史学正, 于东升, 等. 不同方法预测河北省土壤有机碳密度空间分布特征的研究[J]. 土壤学报, 2005, 42(3): 379-385. Zhao Y C, Shi X Z, Yu D S, et al. Different methods for prediction of spatial patterns of soil organic carbon density in Hebei province, China[J]. Acta Pedologica Sinica, 2005, 42(3): 379-385. DOI:10.3321/j.issn:0564-3929.2005.03.005 |
| [13] |
赵明松, 张甘霖, 吴运金, 等. 江苏省土壤有机质含量时空变异特征及驱动力研究[J]. 土壤学报, 2014, 51(3): 448-458. Zhao M S, Zhang G L, Wu Y J, et al. Temporal and spatial variability of soil organic matter and its driving force in Jiangsu province, China[J]. Acta Pedologica Sinica, 2014, 51(3): 448-458. |
| [14] |
李可, 杨勇, 刘亚军, 等. 基于回归克里格的河北省土壤有机质时空变化特征研究[J]. 中国土壤与肥料, 2020(3): 1-7. Li K, Yang Y, Liu Y J, et al. Characteristics of spatiotemporal variation of soil organic matter in Hebei province based on regression Kriging[J]. Soils and Fertilizers Sciences in China, 2020(3): 1-7. |
| [15] |
曹婧, 陈怡平, 毋俊华, 等. 近40年陕西省农田土壤有机质时空变化及其影响因素[J]. 地球环境学报, 2022, 13(3): 331-343. Cao J, Chen Y P, Wu J H, et al. Temporal and spatial variation of soil organic matter in Shaanxi province in the past 40 years and its influencing factors[J]. Journal of Earth Environment, 2022, 13(3): 331-343. |
| [16] |
董秀茹, 刘浩洋, 刘洪彬. 基于耕地资源质量分类的辽宁省耕地土壤条件及空间分布特征分析[J]. 土壤通报, 2021, 52(5): 1020-1027. Dong X R, Liu H Y, Liu H B. Cultivated soil conditions and spatial distribution characteristics based on cultivated land quality classification in Liaoning province[J]. Chinese Journal of Soil Science, 2021, 52(5): 1020-1027. |
| [17] |
王琦, 常庆瑞, 落莉莉, 等. 陕西省农田土壤有机质时空变异与驱动因子定量研究[J]. 农业机械学报, 2022, 53(11): 349-359. Wang Q, Chang Q R, Luo L L, et al. Spatiotemporal variation and driving factors for cultivated soil organic matter in Shaanxi province[J]. Transactions of the Chinese Society for Agricultural Machinery, 2022, 53(11): 349-359. |
| [18] |
齐雁冰, 王茵茵, 陈洋, 等. 基于遥感与随机森林算法的陕西省土壤有机质空间预测[J]. 自然资源学报, 2017, 32(6): 1074-1086. Qi Y B, Wang Y Y, Chen Y, et al. Soil organic matter prediction based on remote sensing data and random forest model in Shaanxi province[J]. Journal of Natural Resources, 2017, 32(6): 1074-1086. |
| [19] |
徐剑波, 宋立生, 夏振, 等. 基于GARBF神经网络的耕地土壤有效磷空间变异分析[J]. 农业工程学报, 2012, 28(16): 158-165. Xu J B, Song L S, Xia Z, et al. Spatial variability of available phosphorus for cultivated soil based on GARBF neural network[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012, 28(16): 158-165. |
| [20] |
连纲, 郭旭东, 傅伯杰, 等. 基于环境相关法和地统计学的土壤属性空间分布预测[J]. 农业工程学报, 2009, 25(7): 237-242. Lian G, Guo X D, Fu B J, et al. Prediction of the spatial distribution of soil properties based on environmental correlation and geostatistics[J]. Transactions of the Chinese Society of Agricultural Engineering, 2009, 25(7): 237-242. |
| [21] |
赵广帅, 李发东, 李运生, 等. GIS空间插值模拟法与土壤类型法估算比较土壤碳储[J]. 农业工程学报, 2014, 30(20): 155-162. Zhao G S, Li F D, Li Y S, et al. GIS spatial interpolation compared with soil type method for estimating soil carbon storage[J]. Transactions of the Chinese Society of Agricultural Engineering, 2014, 30(20): 155-162. |
| [22] |
李启权, 王昌全, 岳天祥, 等. 基于定性和定量辅助变量的土壤有机质空间分布预测——以四川三台县为例[J]. 地理科学进展, 2014, 33(2): 259-269. Li Q Q, Wang C Q, Yue T X, et al. Prediction of distribution of soil organic matter based on qualitative and quantitative auxiliary variables: a case study in Santai county in Sichuan province[J]. Progress in Geography, 2014, 33(2): 259-269. |
| [23] |
郭旭东, 傅伯杰, 陈利顶, 等. 河北省遵化平原土壤养分的时空变异特征——变异函数与Kriging插值分析[J]. 地理学报, 2000, 55(5): 555-566. Guo X D, Fu B J, Chen L D, et al. The spatio-temporal variability of soil nutrients in Zunhua plain of Hebei province: semivariogram and Kriging analysis[J]. Acta Geographica Sinica, 2000, 55(5): 555-566. |
| [24] |
江叶枫, 孙凯, 郭熙, 等. 基于环境因子和邻近信息的土壤属性空间分布预测[J]. 环境科学研究, 2017, 30(7): 1059-1068. Jiang Y F, Sun K, Guo X, et al. Prediction of spatial distribution of soil properties based on environmental factors and neighbor information[J]. Research of Environmental Sciences, 2017, 30(7): 1059-1068. |
| [25] |
谢梦姣, 王洋, 康营, 等. 人工神经网络与普通克里金插值法对土壤属性空间预测精度影响研究[J]. 生态与农村环境学报, 2021, 37(7): 934-942. Xie M J, Wang Y, Kang Y, et al. Accuracy study of spatial predicting in soil attributes based on interpolations by artificial neural network and ordinary Kriging[J]. Journal of Ecology and Rural Environment, 2021, 37(7): 934-942. |
| [26] |
张世文, 张立平, 叶回春, 等. 县域土壤质量数字制图方法比较[J]. 农业工程学报, 2013, 29(15): 254-262. Zhang S W, Zhang L P, Ye H C, et al. Comparison of digital mapping methods of regional soil quality[J]. Transactions of the Chinese Society of Agricultural Engineering, 2013, 29(15): 254-262. |
| [27] |
李龙, 姚云峰, 秦富仓, 等. 小流域土壤有机碳密度空间变异特征的尺度效应研究[J]. 土壤, 2014, 46(5): 787-792. Li L, Yao Y F, Qin F C, et al. Scale-dependency of spatial variability of soil organic carbon density in small watershed[J]. Soils, 2014, 46(5): 787-792. |
| [28] | Tziachris P, Aschonitis V, Chatzistathis T, et al. Assessment of spatial hybrid methods for predicting soil organic matter using DEM derivatives and soil parameters[J]. CATENA, 2019, 174: 206-216. DOI:10.1016/j.catena.2018.11.010 |
| [29] |
刘明杰, 徐卓揆, 郜允兵, 等. 基于机器学习的稀疏样本下的土壤有机质估算方法[J]. 地球信息科学学报, 2020, 22(9): 1799-1813. Liu M J, Xu Z K, Gao Y B, et al. Estimating soil organic matter based on machine learning under sparse sample[J]. Journal of Geo-information Science, 2020, 22(9): 1799-1813. |
| [30] | Wang Z, Du Z P, Li X Y, et al. Incorporation of high accuracy surface modeling into machine learning to improve soil organic matter mapping[J]. Ecological Indicators, 2021, 129. DOI:10.1016/j.ecolind.2021.107975 |
| [31] |
江叶枫, 郭熙, 叶英聪, 等. 应用集成BP神经网络模型预测土壤有机质空间分布[J]. 江苏农业学报, 2017, 33(5): 1044-1050. Jiang Y F, Guo X, Ye Y C, et al. Spatial distribution of soil organic matter predicted by BP neural network ensemble model[J]. Jiangsu Journal of Agricultural Sciences, 2017, 33(5): 1044-1050. |
| [32] |
张宏帅, 朱高龙, 吴家煜, 等. 基于BP神经网络与Kriging结合的土壤有机质空间分布模拟——以福建省华安县为例[J]. 亚热带农业研究, 2021, 17(1): 40-47. Zhang H S, Zhu G L, Wu J Y, et al. Simulation of spatial distribution simulation of soil organic matter based on BP neural network and Kriging interpolation—Taking Hua'an county, Fujian province as an example[J]. Subtropical Agriculture Research, 2021, 17(1): 40-47. |
| [33] |
黄思华, 濮励杰, 解雪峰, 等. 面向数字土壤制图的土壤采样设计研究进展与展望[J]. 土壤学报, 2020, 57(2): 259-272. Huang S H, Pu L J, Xie X F, et al. Review and outlook of designing of soil sampling for digital soil mapping[J]. Acta Pedologica Sinica, 2020, 57(2): 259-272. |
| [34] |
杨琳, 朱阿兴, 秦承志, 等. 一种基于样点代表性等级的土壤采样设计方法[J]. 土壤学报, 2011, 48(5): 938-946. Yang L, Zhu A X, Qin C Z, et al. A soil sampling method based on representativeness grade of sampling points[J]. Acta Pedologica Sinica, 2011, 48(5): 938-946. |
| [35] | McBratney A B, Odeh I O A, Bishop T F A, et al. An overview of pedometric techniques for use in soil survey[J]. Geoderma, 2000, 97(3-4): 293-327. |
| [36] | Amundson R, Harden J, Singer M. Factors of Soil Formation: A Fiftieth Anniversary Retrospective[M]. John Wiley & Sons, Ltd., 1994. |
| [37] | Phachomphon K, Dlamini P, Chaplot V. Estimating carbon stocks at a regional level using soil information and easily accessible auxiliary variables[J]. Geoderma, 2010, 155(3-4): 372-380. |
| [38] |
范胜龙. 农用地分等中样点布设对表征土壤有机碳空间变异的尺度效应研究[D]. 南京: 南京农业大学, 2011. Fan S L. Scale effect of sampling point allocation on detecting spatial variability of soil organic carbon in agricultural land classification[D]. Nanjing: Nanjing Agricultural University, 2011. |
| [39] | Sumfleth K, Duttmann R. Prediction of soil property distribution in paddy soil landscapes using terrain data and satellite information as indicators[J]. Ecological Indicators, 2008, 8(5): 485-501. |
| [40] |
邓燕红. 不同地貌类型区表征土壤有机质空间变异的空间插值模型及尺度效应研究[D]. 福州: 福建农林大学, 2015. Deng Y H. Scale effect and spatial interpolation models on detecting spatial variability of soil organic matter in different geomorphology types[D]. Fuzhou: Fujian Agriculture and Forestry University, 2015. |
| [41] | Rasmussen C, Heckman K, Wieder W R, et al. Beyond clay: towards an improved set of variables for predicting soil organic matter content[J]. Biogeochemistry, 2018, 137(3): 297-306. |
| [42] |
朱阿兴, 杨琳, 樊乃卿, 等. 数字土壤制图研究综述与展望[J]. 地理科学进展, 2018, 37(1): 66-78. Zhu A X, Yang L, Fan N Q, et al. The review and outlook of digital soil mapping[J]. Progress in Geography, 2018, 37(1): 66-78. |
| [43] | 蒯本信. 1: 25万宁夏土壤图的编制设计[J]. 土壤, 1991, 23(3): 140-142. |
| [44] |
郭少阳, 郑蝉金, 陈彦垒. 方差分析与回归分析的整合: 虚拟变量与设计矩阵[J]. 统计与决策, 2018, 34(12): 25-28. Guo S Y, Zhen C J, Chen Y L. The integration between analysis of variance and linear regression: dummy variables and design matrixes[J]. Statistics and Decision, 2018, 34(12): 25-28. |
| [45] |
戴金辉. 虚拟变量回归及其应用[J]. 统计与决策, 2019, 35(5): 77-80. Dai J H. Dummy variable regression and its application[J]. Statistics and Decision, 2019, 35(5): 77-80. |
| [46] |
邱锡鹏. 神经网络与深度学习[M]. 北京: 机械工业出版社, 2020. Qiu X P. Neural networks and deep learning[M]. Beijing: China Machine Press, 2020. |
| [47] | Xue J K, Shen B. A novel swarm intelligence optimization approach: sparrow search algorithm[J]. Systems Science & Control Engineering, 2020, 8(1): 22-34. |
| [48] |
薛建凯. 一种新型的群智能优化技术的研究与应用——麻雀搜索算法[D]. 上海: 东华大学, 2020. Xue J K. Research and application of a novel swarm intelligence optimization technique: sparrow search algorithm[D]. Shanghai: Donghua University, 2020. |
| [49] | Feng J H, Zhang J, Zhu X S, et al. A novel chaos optimization algorithm[J]. Multimedia Tools and Applications, 2017, 76(16): 17405-17436. |
| [50] | Yang X S. Nature-inspired metaheuristic algorithms[M]. Beckington: Luniver Press, 2008. |
| [51] | 师长兴, 王随继, 许炯心, 等. 黄河宁蒙段河道洪峰过程洪-床-岸相互作用机理[M]. 北京: 科学出版社, 2016. |
| [52] | 张厚军, 鲁俊, 张建, 等. 黄河上游宁蒙河段治理研究[M]. 北京: 科学出版社, 2020. |
| [53] | 张晴雯, 张爱平, 杨正礼. 黄河上游宁夏灌区稻田氮素平衡与污染控制[M]. 北京: 中国农业科学技术出版社, 2014. |
| [54] | 马玉兰. 宁夏土壤有机质、常量及微量元素的地理规律和丰欠类型[J]. 宁夏农林科技, 1992(2): 5-8. |
| [55] |
尉芳, 刘京, 夏利恒, 等. 陕西渭北旱塬区农田土壤有机质空间预测方法[J]. 环境科学, 2022, 43(2): 1097-1107. Wei F, Liu J, Xia L H, et al. Spatial prediction method of farmland soil organic matter in Weibei dryland of Shaanxi province[J]. Environmental Science, 2022, 43(2): 1097-1107. |
| [56] |
李维友, 段良霞, 谢红霞, 等. 基于条件拉丁超立方抽样的县域耕地土壤有机质空间插值合理样本密度的确定[J]. 土壤通报, 2022, 53(3): 505-513. Li W Y, Duan L X, Xie H X, et al. Determination of reasonable sample density for spatial interpolation of soil organic matter in cultivated land of county region based on conditional Latin hypercube sampling[J]. Chinese Journal of Soil Science, 2022, 53(3): 505-513. |
 2024, Vol. 45
2024, Vol. 45


