2. 农业部西北植物营养与农业环境重点实验室, 杨凌 712100
2. Key Laboratory of Plant Nutrition and the Agri-environment in Northwest China, Ministry of Agriculture, Yangling 712100, China
土壤有机质(soil organic matter, SOM)增强了土壤中水分和养分的保持能力[1], 其活性组分促进了微生物群落的健康发展, 作为土壤肥力的重要组成成分, SOM对维持高水平的粮食生产具有至关重要的意义.由于有机质能够对气候变化给出潜在反馈, 以及其在全球碳循环中的关键作用和在保持土壤质量方面的重要性, 因而有机质被普遍认为是土壤功能和生态系统服务的关键属性[2~7].
随着“3S”技术的发展, 数字土壤制图领域中的多种方法和模型被广泛应用于预测土壤属性的空间分布, 其中, 基于相邻采样点权重对未知点进行预测的普通克里格插值法(ordinary Kriging, OK)因其具有操作容易和原理简单的特点而得到了普遍应用[8, 9].但OK法强烈依赖于样本点的数量和质量且不考虑环境因素的影响[10], 而土壤自身属性受到地形和外界活动等众多因子的影响[11~13], 因此, 在复杂条件下使用OK法无法得到较高的预测精度.为使预测结果更准确, 有学者将影响预测值的环境因子作为辅助变量参与模型的建立.国外学者Moura-Bueno等[14]的研究为探究将环境数据作为协变量输入模型是否是一种有前途的策略, 建立了6个协变量集, 结果表明包含所有协变量的集表现最佳, 与其他模型相比其预测精度提高了12%; 国内学者夏子书等[15]和朱福斌等[16]在其研究中均利用了辅助变量参与预测模型的建立, 结果表明相比普通克里格等方法, 引入协变量辅助预测的模型精度都得到了提升, 诸多研究表明, 在预测模型中引入协变量是提高预测精度、减少预测误差的有效手段.在众多的预测方法中, GWR、PLS和RF模型的应用较多且精度较高, 如王春帅等[17]的研究构建GWR反演模型, 试图实现对农田土壤中Ni的预测, 经验证, GWR预测模型的预测精度高达96.51%; Wang等[18]的研究构建了农用地土壤重金属浓度的预测模型, 结果表明RF模型能够更好地预测土壤中重金属的浓度和空间分布.
然而, 上述的研究也存在一定缺陷, 在因子选取上, 部分研究仅考虑自然因素对预测变量的影响, 缺少对人为因素的探究; 在研究区尺度上, 国内的研究多是在小尺度区域上进行的, 在环境复杂的大尺度区这些算法的适用性和精度如何还有待讨论; 在预测模型的比较上, 目前的研究中缺少RF、GWR和PLS等模型的对比分析.鉴于此, 本文以地形地貌复杂的陕西渭北旱塬区为研究对象, 以与农田SOM含量相关性强的影响因子为切入点, 从地形因素、土壤属性和社会经济这3个方面选取影响因子并借助地理探测器得到主要影响因子, 选择随机森林和地理加权回归等模型, 通过对其预测精度的对比分析确定最优预测方法, 以期找到适合环境复杂区的SOM含量预测的最优模型.
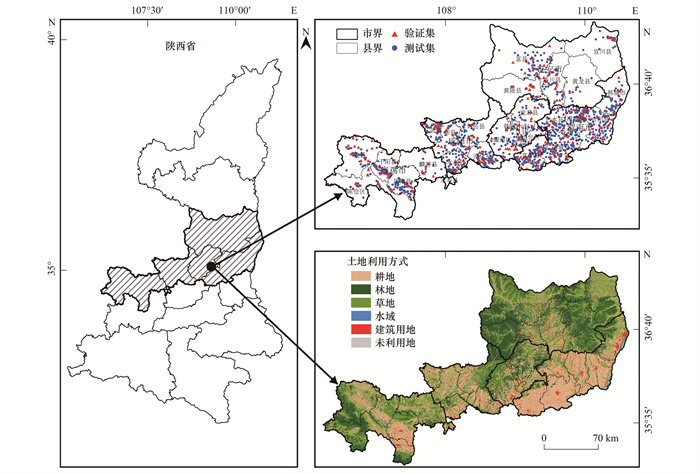
1 材料与方法 1.1 研究区概况渭北旱塬区处于陕西黄土高原丘陵沟壑区与渭河冲积平原的过渡区域(北纬34°22′~36°14′, 东经106°29′~110°36′), 包括宝鸡市、咸阳市、渭南市、延安市和铜川市这5个地市中的25个区县(图 1), 总面积3.96万km2, 约占陕西省总面积的19.26%, 全省粮、油、果等一半以上的生产基地都分布在这一区域, 是陕西省乃至我国西北地区重要的粮食生产基地.研究区海拔331~2 452 m, 区域内地形起伏较大, 地势从南到北逐步升高, 大体上呈阶梯状分布, 地貌复杂以高原沟壑为主.该区光热资源丰富, 年平均气温在8.6~13.5℃之间, 年降雨量520~650 mm, 降水多集中在7~9月, 降水量较少且年内分配不均.
|
图 1 研究区概况及土壤样点分布 Fig. 1 Overview of the study area and distribution of soil samples |
结合研究区实际, 在全区农用地上布设大田采样点, 采样点覆盖整个研究区域, 按照“随机”、“等量”和“多点混合”的原则进行土样的采集, 同时用GPS记录样点的经纬度, 最终得到SOM预测精度评估的实测样点数据(样点来自于2018年进行耕地质量评价时采集分析的数据)共1 432个, 实测样点数据均为耕层(取样深度在0~20 cm)样品, 各县(市县)样点统计情况见表 1, 样点分布见图 1.土壤有机质测定采用油浴加热重铬酸钾容量法、土壤全氮测定采用半微量开氏法、土壤速效钾测定采用乙酸铵浸提-火焰光度法、土壤有效磷测定采用碳酸氢铵浸提-钼锑抗比色法、pH测定采用电位法[19, 20].使用SPSS软件按标准方差的倍数识别特异值, 一般特异值定为样品均值m加减3倍均方差δ, 即m±3δ, 然后用正常值的最大值和最小值替代特异值[11].再通过ArcGIS 10.3软件地统计工具中的要素子集功能对监测点数据集进行均匀随机划分, 选取样本数据集的80%作为测试集数据(1 146个), 20%作为验证集数据(286个).
|
|
表 1 研究区县(市县)样点统计数据 Table 1 Statistical data of sample points of counties (cities) in the study area |
本文采用的2018年土地利用/土地覆被数据来源于中国科学院资源环境科学数据中心(http://www.resdc.cn), 土地利用数据的遥感解译主要使用了Landsat 8遥感影像数据; DEM数据和行政区划数据来源于地理国情监测云平台(http://www.dsac.cn); 海拔、坡度和坡向数据从DEM数据中提取得到; 社会经济数据来源于陕西省统计年鉴[21]; 土壤类型、土壤质地、地貌类型和土地利用方式是调查采样时获取的.
1.3 研究方法 1.3.1 地理探测器地理探测器[22](Geodetector)假设影响某个因变量变化的自变量在空间上具有差异性, 如果自变量对因变量有重要影响, 则该自变量对因变量的发生与发展具有重要意义, 并且二者的空间分布应该具有相似性[23, 24].因子检测器, 通过计算q统计量来衡量自变量对因变量的解释能力[25, 26], 根据二者间的相关性程度选取主要影响因子参与因变量的预测建模.交互探测器, 通过对两个因子的共同作用与两个因子单独的作用进行比较, 从两个因子交互作用和单独各个因子交互作用之和的解释力来分析, 主要交互作用的表现形式见表 2.
|
|
表 2 因子交互探测关系 Table 2 Factor interaction detection relationship |
1.3.2 地理加权回归模型和偏最小二乘回归模型
地理加权回归模型[27, 28](geographically weighted regression, GWR)引入对不同区域的影响进行估计, 能够反映参数在不同空间的空间非平稳性, 使变量间的关系可以随空间位置的变化而变化, 其结果更加符合客观实际.
偏最小二乘回归模型(partial least squares, PLS)结合了MSR中提取主成分的方法, 对数据进行信息处理和筛选, 具有尽可能多地提取自变量信息且不删除样本点的特点, 能够保证自变量与因变量之间最大的相关性[29, 30], 在解决自变量多重共线性和样本数量较少等问题上具有很好的表现[31~33].
1.3.3 GWRPLS模型在GWR模型的基础上构建的扩展模型GWRPLS, 可以同时兼顾地理加权回归方法的局部变化系数以及对模型残差进行偏最小二乘回归建模并赋予其全局固定系数[34].理论上, 该模型可以通过空间异质性更好地减少实测值和预测值之间的误差.公式如下:
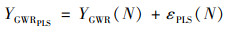
|
(1) |
式中, YGWRPLS为GWRPLS预测值, YGWR(N)为经过GWR模型插值获得的预测值, εPLS(N)为经过PLS模型建模得到的残差值.
1.3.4 随机森林模型在CART模型的基础上开发得到的随机森林模型(random forest, RF)不仅可以较好地处理变量之间复杂的非线性关系[35], 同时克服了过度拟合和计算复杂等缺陷, 具有对大量定性数据和定量数据进行简单处理的优点[36, 37], RF模型通过对大量分类树的汇总提高了模型的预测精度[38], 是取代神经网络等传统机器学习方法的新模型.在建立随机森林算法的过程中, ntree和mtry是两个非常重要的自定义参数, 本文将mtry值设为变量个数的开方值, 通过绘制模型误差与决策树数量关系图寻找最佳决策树数目.
1.3.5 模型验证均方误差(MSE)是衡量“平均误差”的一种较方便的方法, 可以评价数据的变化程度, MSE的值越小, 说明预测模型描述实验数据具有更好的精确度.平均绝对误差(MAE)和均方根误差(RMSE)的取值范围均为[0, +∞], 当预测值与真实值完全吻合时等于0, 即完美模型; 误差越大, 该值越大.预测偏差(RPD)用于模型预测能力的判断, RPD<1.4, 说明模型预测能力差, 无法对数据样本进行预测; 1.4≤RPD≤2, 说明模型预测能力较为一般, 能够对数据样本进行粗略预测; RPD>2, 说明预测模型能力极好, 能够对样本数据进行精确合理的预测.皮尔森相关系数(r)是相关性系数, 其取值范围为[-1, 1], 用于判断实测值和预测值之间是否存在着一定的线性相关关系, 若r>0, 表示实测值和预测值正相关; 若r<0, 表示实测值和预测值负相关[31, 39, 40].
2 结果与分析 2.1 SOM含量的描述性统计由表 3可知, 研究区农田ω(SOM)平均值为15.14 g ·kg-1, 范围在2.25~30.23 g ·kg-1之间, 依照全国第二次土壤普查养分分级标准, SOM含量处于分级标准的二~六级, 最小值和最大值之间差异显著; 研究区SOM含量的标准差为4.54, 表明不同县(市县)之间的土壤数据具有一定的波动; 从变异程度看, SOM含量的变异系数为30.00%, 属于中等变异, 表明土壤有机质在空间分布上具有一定差异, 适合进行空间局部估计.测试集样点ω(SOM)范围为2.25~30.23 g ·kg-1, 验证集样点ω(SOM)在4.38~30.23 g ·kg-1之间, 验证集样点最小值明显高于测试集样点, 测试集样点的中位数和标准差均略高于验证集样点, 其平均值略低于验证集样点, 变异系数分别为30.11%和29.57%, 均属于中等变异水平.
|
|
表 3 SOM含量基本统计特征 Table 3 Basic statistical characteristics of SOM content |
2.2 影响因子提取
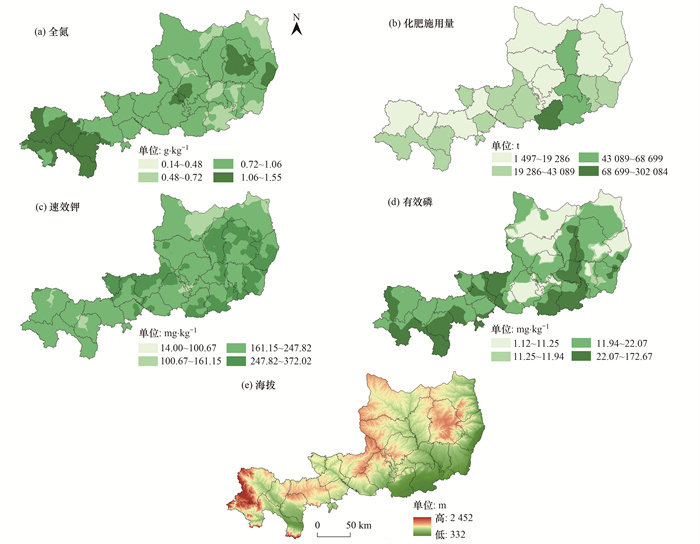
从地形因素、土壤属性和社会经济这3个方面选取了11种影响因子, 即化肥施用量、全氮、有效磷、速效钾、缓效钾、pH、海拔、坡度、坡向、土壤类型和土壤质地.利用地理探测器中的风险因子探测器计算各影响因子的q统计量, q值由大到小排序为: 全氮(0.521)>化肥施用量(0.345)>速效钾(0.162)>有效磷(0.099)>海拔(0.089)>土壤类型(0.067)>土壤质地(0.037)>缓效钾(0.035)>pH(0.029)>坡向(0.024)>灌溉能力(0.014)>坡度(0.013).因子探测结果说明, 不同影响因子对SOM含量的解释力程度不同, 其中土壤中全氮对SOM空间变异的影响最大, 主要原因是土壤有机质与全氮之间关系密切, SOM是土壤氮素的主要存在场地[41], 氮素的贮存和转化受到SOM累积和分解的直接影响, 这一现象与先前学者的研究结果一致[42~44]; 其次, 化肥施用量对SOM的解释力达到0.345, 表明渭北旱塬区SOM空间分异除受自然因素的影响较大外, 社会经济因素对其的影响力也较大, 人类活动的影响在一定程度上影响了研究区SOM含量变化.本研究选择前5个因子(全氮、化肥施用量、速效钾、有效磷和海拔)作为建模的辅助变量, 其他因子的解释力太低, 故不参与后续建模, 主要影响因子空间分布状况如图 2所示.
|
图 2 研究区主要影响因子空间分布情况 Fig. 2 Spatial distribution of major influencing factors in the study area |
地理探测器中的交互探测模块能够定量地表征两个影响因子对于土壤有机质含量的作用关系, 可以判断两个因子交互作用对SOM含量的影响相比于单个因子对SOM含量的影响为强化作用还是弱化作用.本文对SOM含量的解释力进行交互作用q统计量分析, 因子交互作用结果见表 4.
|
|
表 4 因子交互作用q值及相应交互关系 Table 4 Factor interaction q value and corresponding interaction relationship |
从研究区主要影响因子交互作用对于SOM含量的解释力结果来看, 在解释力较大的驱动因子中从大到小排列的顺序如下: 化肥施用量∩全氮(81%)>全氮∩海拔(68%)>全氮∩有效磷=全氮∩速效钾(58%), 其中, 海拔和全氮之间的交互作用表现为非线性加强; 化肥施用量、有效磷、速效钾和全氮之间则呈现出双线性加强的交互作用, 说明化肥施用量、有效磷和速效钾因素在对SOM含量的作用力方面都分别与全氮具有互相增强的关系, 使其各自影响力增大.
对因子交互作用的解释力与单个因子独立起作用的解释力值和q(A)+q(B)进行分析, 各因子之间的交互作用q值均大于各单因子的q值, 因子交互效果呈现为双线性加强和非线性加强.说明各因子的交互作用对SOM含量的影响不是简单的线性相加, 而是双线性加强和非线性加强的效应, 研究区各影响因子间相互作用对SOM含量空间分异的影响均高于单因子对SOM含量空间分异的影响.
2.3 SOM预测模型构建根据地理探测器的结果, 选择全氮、化肥施用量、速效钾、有效磷和海拔这5种影响因子作为协变量参与所有预测模型的建立.
采用测试集数据, 利用GWR 4.0软件拟合地理加权回归模型, 决定系数为0.85, 拟合系数见表 5.参与GWR建模的主要影响因子系数有正有负, 其中全氮的系数中值最大为15.34, 化肥施用量的系数中值最小, 仅为0.000 001, 所有因子的系数中值均大于0, 与SOM呈正相关; Moran指数的范围在0.210~0.907之间, 海拔和化肥施用量的Moran指数分别为0.906和0.907, 呈现出强烈的空间自相关性.
|
|
表 5 地理加权回归模型预测参数统计特征 Table 5 Statistical characteristics of the prediction parameters of the GWR model |
基于SIMCA 14.1软件建立PLS预测模型, 如表 6所示, 随着主成分数量的增加, 因变量和自变量的累计值逐渐增大, 主成分数量为3时, Y累积量达到最大值0.656, 同时, 决定系数升高至0.645, 当主成分数量继续增加时, Y累积量不再变化, 决定系数随之减少.因此, 本研究的PLS模型选取前3种主成分进行模型的构建.
|
|
表 6 偏最小二乘回归模型预测参数统计特征 Table 6 Statistical characteristics of prediction parameters of partial least squares regression model |
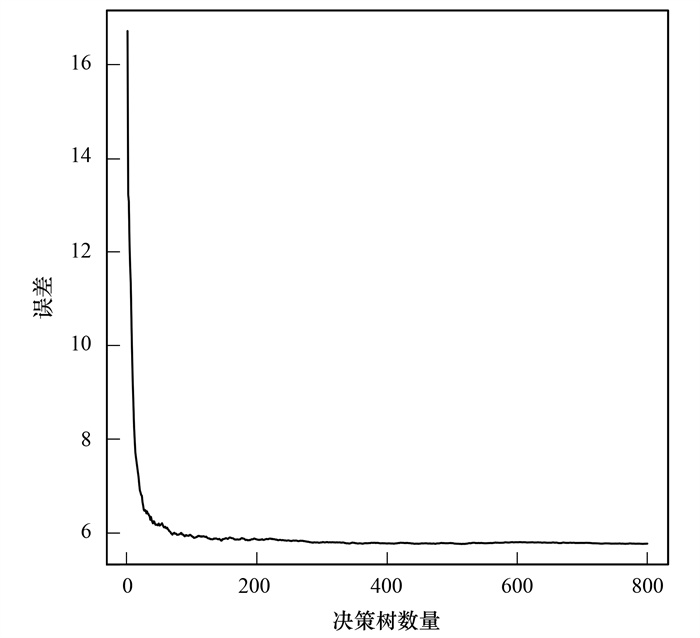
随机森林作为一种组合算法, 在生成森林的过程中, 单棵树的训练数据集通过自助法从原训练数据集中抽取, 在单棵树的分裂过程中, 每个内部分裂节点的分裂属性也是分别从原输入因子中抽取, 随机森林的最终预测结果综合多棵树的结果决定.用R 4.0.3软件中的random Forest软件包进行预测, 将每棵树使用的特征个数mtry值设置为2, 森林中树的个数ntree值设置为800, 模型误差结果见图 3, 其中的横坐标为随机森林模型中树的棵数, 纵坐标为交叉验证后得到模型的均方误差, 可以发现模型在树的棵数达到400时基本趋于稳定, 所以ntree在该模型中设置为400.
|
图 3 模型误差与决策树数量关系 Fig. 3 Relationship between model error and the number of decision trees |
使用5种模型对SOM含量进行预测, 结果见表 7和图 4.从表 7可以看出, 除GWRPLS以外, 其余4种模型得到的SOM的最小值均在6 g ·kg-1以上, 与测试集样点的最小值2.25 g ·kg-1相比, 低值区有一定程度的压缩, 测试集中仅有21个样点的SOM含量值小于6 g ·kg-1, 其中有15个点在宜川县集中分布, 其余低值点在研究区中零星分布, 因此在建模过程中低值点受到周边点的影响, 导致预测结果偏高, 而GWRPLS方法由于兼顾了全局和局部因素的影响, 能较好地处理预测时产生的误差, 使结果值更贴近实际情况.
|
|
表 7 土壤有机质含量预测结果统计特征/g ·kg-1 Table 7 Statistical characteristics of soil organic matter content prediction results/g ·kg-1 |
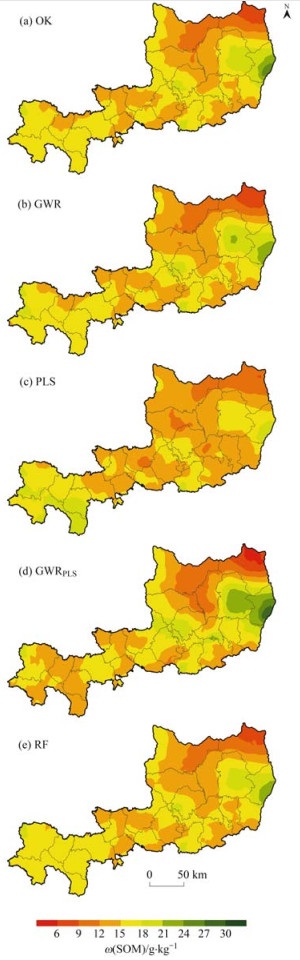
|
图 4 不同模型SOM含量预测值空间分布 Fig. 4 Spatial distribution of predicted values of SOM content in different models |
不同预测模型获得的SOM含量空间分布情况如图 4所示, 图 4(a)为对测试集中SOM的实测值进行OK插值得到的结果.通过对比可知, 5种方式得到的SOM空间分布特征较为相似, 呈现出北部、东北部地区含量低, 西部、东南部地势相对平缓的平原地区含量高的空间分布趋势, 研究区SOM含量的高值区主要分布在渭南市韩城市, 低值区则集中于延安市宜川县.出现高值区的原因可能是韩城市土壤全氮和速效钾含量高且该地区地势平坦有利于有机质的积累; 宜川县处于黄土高原丘陵沟壑区, 地势西高东低, 地形起伏较大, 雨水对土壤的冲刷能力大, 水土流失强, 耕作环境条件较差, SOM含量低, 不容易贮存, 因此出现了低值区.此外, 在宝鸡市陇县西北部也有少量区域SOM含量高, 主要原因是该地区海拔高, 气温相对较低, 土性凉, 土壤中微生物活动弱, 有机质分解缓慢.
2.5 不同模型的预测精度分析利用验证集数据, 将5种预测方法的精度指标进行对比, 结果见表 8.从中可知, OK模型的各项精度指标均为最差, 说明在渭北旱塬区进行SOM预测时加入辅助因子是有必要的; PLS模型的MSE最大(6.042), RF模型的MSE最小(1.733), 说明在渭北旱塬地区, 利用偏最小二乘回归方法进行农田SOM预测的精确度最差, 而通过随机森林方法得到的SOM精确度较好; 不同预测模型的RMSE和MAE由大到小排序结果皆为: PLS>GWR>GWRPLS>RF, 进一步说明了相比于其他几种预测模型, RF的预测精度更高; 除PLS模型的PRD介于1.4~2以外, GWR、GWRPLS和RF模型的RPD均大于2, 说明这3种模型的预测能力强, 得到的预测结果更为精确合理; 从r来看, RF法的相关性系数最高, 表明通过随机森林方法得到的预测值和样本实测值之间的相关性最高.
|
|
表 8 预测模型精度指标统计特征1) Table 8 Statistical characteristics of precision indexes of prediction model |
对比GWR、PLS和GWRPLS这3种预测模型的精度指标可知, GWR的MSE、RMSE和MAE值比PLS均有不同程度的降低, 预测偏差和相关性系数有所升高, 说明相比于只考虑全局数量关系的模型而言, GWR这种引入了局部空间位置关系的模型预测效果更好; 基于GWR预测结果和PLS预测残差值建立的GWRPLS模型, 在各项指标的表现上有一定提升, MSE、RMSE和MAE减小, RPD和r增加, 这一现象表明在研究区中进行SOM含量的预测工作时, 要重视模型残差对于预测结果的影响.
3 讨论由于受到环境因素的影响, 耕层SOM含量的预测存在一定的不确定性, 因此在考虑耕层SOM与影响因子之间关系的基础上, 探讨不同预测模型在环境复杂区域土壤有机质预测的适用性, 对提高农田SOM的预测精度具有科学指导意义.
3.1 耕层SOM空间分布与主要影响因子的关系整体上看, 基于5种模型得到的SOM空间分布情况几乎一致, 呈现出东北部高、东南部低的趋势.相比于普通克里格法得到的结果, PLS预测的SOM空间分布图高、低值区较不明显, 说明PLS法在预测时主要关注SOM与辅助变量间的全局关系, 忽略了相邻样本之间的局部关系; GWR和RF预测的空间分布则具有较好的表现, 说明这两种方法在建模时兼顾了SOM的空间异质性和相似性; 而利用GWRPLS法得到的SOM空间分布特征变化更加明显, 说明兼顾了全局数量关系的局部空间位置模型得到了一定程度的优化.对比主要影响因子与SOM的分布情况, 可以看出土壤全氮、速效钾和有效磷与有机质含量呈正相关, 高值区和低值区具有一定的对应关系, 如在宜川县北部, 4种土壤养分的含量值都很低, 而在韩城市, 都出现了4种营养成分的高值区域.自然因素中, 土壤全氮与有机质之间的相关性最明显, 其q值达到0.521, 土壤有机质是氮素的主要贮存场所, 土壤表层中约有80% ~97%的氮[33]存在于SOM之中, 因此两者关系紧密.人为因素中, 本研究只引入了化肥施用量一种因子, 由于化肥施用量的统计单位是县(市县)级, 因此在空间分布上与SOM的对照关系并不明显, 但其q值仍达到了0.345, 说明除土壤自身属性外, 人类活动对SOM的含量值产生较大的影响.本研究考虑的影响因子仍有一定的局限, 可在后续的研究中增加更多环境因子, 有研究将气温、降水、NDVI和光谱指数等因素作为优化预测模型的协变量[45~47], 并且取得了不错的预测精度, 如赵明松等[48]的研究利用年均温、物理性黏粒等因子预测SOM的空间分布, 建模结果优于传统的全局回归建模; 唐海涛等[49]的研究选取归一化指数、比值指数等作为辅助变量, 采用CARS算法预测土壤中有机质的含量, 结果表明模型预测精度好且稳定性高.
3.2 预测模型的精度相比于普通克里格插值法, GWR、RF等预测方法均能在一定程度上提高耕层SOM含量的空间预测精度.为进一步探究不同预测模型的精度, 对耕层SOM实测值和预测值进行线性拟合, 结果如图 5所示.从中可以看出, 除OK法得到的SOM含量的预测值和实测值之间的R2低于0.3以外, 其余4种模型的决定系数均在0.6以上, GWRPLS和RF的R2更是达到了0.937和0.945, 预测值和实测值之间表现出了很强的相关性, 以OK法为参照, GWR、PLS、GWRPLS和RF的预测精度分别提高了49.83%、34.68%、64.60%和65.03%, 较前人的研究结果有所增加[34]; 对比OK法得到的结果, 其余4种方法得到的拟合点分布的离散程度明显降低, 基本集中在1 ∶1线附近, GWRPLS和RF得到的拟合点分布十分紧密, 模型的预测效果得到明显提升.

|
图 5 不同预测方法的预测值和实测值线性回归分析 Fig. 5 Linear regression analysis of predicted values and measured values of different prediction methods |
预测模型精度指标和线性回归分析结果基本一致, 预测模型的精度由大到小排序为: RF>GWRPLS>GWR>PLS>OK.对前4种预测模型进行分析, 考虑了空间异质性的局部模型预测效果高于全局模型, 结合了二者优势的扩展模型预测精度得到了进一步提升, 说明该扩展模型不仅可以考虑研究区整体的空间非平稳性, 并且可以较好地解释存在预测残差区域的空间自相关性; 随机森林模型的预测优势十分明显, 较好地处理了各变量之间的复杂关系, 除RPD略低于GWRPLS以外, 其余精度指标值均优于其他模型, 说明相比于其他几种预测模型, RF模型更适合用于渭北旱塬区SOM的预测中.
综合所有指标的分析结果, RF模型的预测精度最高, GWRPLS的预测精度虽低于RF法, 但相差较小, 二者在渭北旱塬区SOM预测上均拥有较好的表现, 因此后续在环境复杂区进行土壤有机质含量预测的研究时, 应优先考虑GWRPLS法和RF法的应用和比较.
4 结论(1) 陕西渭北旱塬区农田样本ω(SOM)均值为15.14 g ·kg-1, 范围在2.25~30.23 g ·kg-1之间.研究区各县(市县)之间条件不同, 其空间分异受到地形、土壤理化性质和耕作制度的影响, 自然环境和耕作条件限制了土壤中的有机质含量, 并且各地区间外源性的肥料施入量不尽相同, 导致有机质含量差异显著.
(2) 因子探测结果显示, 影响研究区耕层SOM含量的主要影响因子分别为全氮(0.521)、化肥施用量(0.345)、速效钾(0.162)、有效磷(0.099)和海拔(0.089); 交互探测结果表现为双线性加强和非线性加强两种交互关系, 说明任意两因子的交互作用均高于单因子对SOM含量的影响.
(3) 5种预测模型中, GWRPLS模型和RF模型表现更突出, 与OK法相比, MSE降至1.775和1.733, RPD升高至3.804和2.710, 相关系数升至0.968和0.972, 拟合精度分别提升了64.60%和65.03%, RF法预测精度略高于GWRPLS模型, 因此在本研究中, 随机森林模型为最优预测模型.
| [1] | Picariello E, Baldantoni D, Izzo F, et al. Soil organic matter stability and microbial community in relation to different plant cover: a focus on forests characterizing Mediterranean area[J]. Applied Soil Ecology, 2021, 162. DOI:10.1016/J.APSOIL.2021.103897 |
| [2] | Machmuller M B, Kramer M G, Cyle T K, et al. Emerging land use practices rapidly increase soil organic matter[J]. Nature Communications, 2015, 6. DOI:10.1038/ncomms7995 |
| [3] | Chen L Y, Liu L, Qin S Q, et al. Regulation of priming effect by soil organic matter stability over a broad geographic scale[J]. Nature Communications, 2019, 10. DOI:10.1038/s41467-019-13119-z |
| [4] | Reis A S, Rodrigues M, dos Santos G L A A, et al. Detection of soil organic matter using hyperspectral imaging sensor combined with multivariate regression modeling procedures[J]. Remote Sensing Applications: Society and Environment, 2021, 22. DOI:10.1016/J.RSASE.2021.100492 |
| [5] | Kopecky M, Peterka J, Kolář L, et al. Influence of selected maize cultivation technologies on changes in the labile fraction of soil organic matter sandy-loam cambisol soil structure[J]. Soil and Tillage Research, 2021, 207. DOI:10.1016/J.STILL.2020.104865 |
| [6] | Manlay R J, Feller C, Swift M J. Historical evolution of soil organic matter concepts and their relationships with the fertility and sustainability of cropping systems[J]. Agriculture, Ecosystems & Environment, 2007, 119(3-4): 217-233. |
| [7] | Liu Y, Lv J S, Zhang B, et al. Spatial multi-scale variability of soil nutrients in relation to environmental factors in a typical agricultural region, Eastern China[J]. Science of the Total Environment, 2013, 450-451: 108-119. DOI:10.1016/j.scitotenv.2013.01.083 |
| [8] |
杨煜岑, 杨联安, 任丽, 等. 基于随机森林的农耕区土壤有机质空间分布预测[J]. 浙江农业学报, 2018, 30(7): 1211-1217. Yang Y C, Yang L A, Ren L, et al. Prediction for spatial distribution of soil organic matter based on random forest model in cul-tivated area[J]. Acta Agriculturae Zhejiangensis, 2018, 30(7): 1211-1217. DOI:10.3969/j.issn.1004-1524.2018.07.15 |
| [9] |
姜赛平, 张怀志, 张认连, 等. 基于三种空间预测模型的海南岛土壤有机质空间分布研究[J]. 土壤学报, 2018, 55(4): 1007-1017. Jiang S P, Zhang H Z, Zhang R L, et al. Research on spatial distribution of soil organic matter in Hainan Island based on three spatial prediction models[J]. Acta Pedologica Sinica, 2018, 55(4): 1007-1017. |
| [10] |
江叶枫, 孙凯, 郭熙, 等. 基于环境因子和邻近信息的土壤属性空间分布预测[J]. 环境科学研究, 2017, 30(7): 1059-1068. Jiang Y F, Sun K, Guo X, et al. Prediction of spatial distribution of soil properties based on environmental factors and neighbor information[J]. Research of Environmental Sciences, 2017, 30(7): 1059-1068. |
| [11] |
王幼奇, 张兴, 赵云鹏, 等. 基于GIS和地理加权回归的砂田土壤阳离子交换量空间预测[J]. 土壤, 2020, 52(2): 421-426. Wang Y Q, Zhang X, Zhao Y P, et al. Interpolation of soil CEC of sandy fields using GIS and geographically weighted regression-kriging[J]. Soils, 2020, 52(2): 421-426. |
| [12] | Alsamamra H, Ruiz-Arias J A, Pozo-Vázquez D, et al. A comparative study of ordinary and residual kriging techniques for mapping global solar radiation over southern Spain[J]. Agricultural and Forest Meteorology, 2009, 149(8): 1343-1357. DOI:10.1016/j.agrformet.2009.03.005 |
| [13] | Dai F Q, Zhou Q G, Lv Z Q, et al. Spatial prediction of soil organic matter content integrating artificial neural network and ordinary kriging in Tibetan Plateau[J]. Ecological Indicators, 2014, 45: 184-194. DOI:10.1016/j.ecolind.2014.04.003 |
| [14] | Moura-Bueno J M, Dalmolin R S D, Horst-Heinen T Z, et al. Environmental covariates improve the spectral predictions of organic carbon in subtropical soils in southern Brazil[J]. Geoderma, 2021, 393. DOI:10.1016/J.GEODERMA.2021.114981 |
| [15] |
夏子书, 白一茹, 王幼奇, 等. 基于GIS和随机森林算法的宁东土壤饱和导水率分布与预测[J]. 水土保持学报, 2021, 35(1): 285-293. Xia Z S, Bai Y R, Wang Y Q, et al. Distribution and prediction of soil saturated hydraulic conductivity in Ningdong based on GIS and random forest algorithm[J]. Journal of Soil and Water Conservation, 2021, 35(1): 285-293. |
| [16] |
朱福斌, 丁世伟, 甘晓玉, 等. 基于三种空间预测方法的安庆市耕地土壤速效钾空间分布预测[J]. 中国土壤与肥料, 2021(1): 1-8. Zhu F B, Ding S W, Gan X Y, et al. Prediction of spatial distribution of available potassium in cultivated soil of Anqing city based on three spatial prediction methods[J]. Soils and Fertilizers Sciences in China, 2021(1): 1-8. |
| [17] |
王春帅, 姚立伟, 刘弋珲, 等. GWR模型下农用地土壤镍空间分布预测[J]. 遥感信息, 2021, 36(1): 43-49. Wang C S, Yao L W, Liu Y H, et al. Prediction of soil nickel spatial distribution in agricultural soil under GWR model[J]. Remote Sensing Information, 2021, 36(1): 43-49. DOI:10.3969/j.issn.1000-3177.2021.01.007 |
| [18] | Wang H Z, Yilihamu Q, Yuan M N, et al. Prediction models of soil heavy metal(loid)s concentration for agricultural land in Dongli: a comparison of regression and random forest[J]. Ecological Indicators, 2020, 119. DOI:10.1016/j.ecolind.2020.106801 |
| [19] |
甲卡拉铁, 喻华, 冯文强, 等. 淹水条件下不同氮磷钾肥对土壤pH和镉有效性的影响研究[J]. 环境科学, 2009, 30(11): 3414-3421. Jia K L T, Yu H, Feng W Q, et al. Effect of different N, P and K fertilizers on soil pH and available Cd under waterlogged conditions[J]. Environmental Science, 2009, 30(11): 3414-3421. DOI:10.3321/j.issn:0250-3301.2009.11.048 |
| [20] |
王军, 傅伯杰, 邱扬, 等. 黄土高原小流域土壤养分的空间异质性[J]. 生态学报, 2002, 22(8): 1173-1178. Wang J, Fu B J, Qiu Y, et al. Spatial heterogeneity of soil nutrients in a small catchment of the Loess Plateau[J]. Acta Ecologica Sinica, 2002, 22(8): 1173-1178. DOI:10.3321/j.issn:1000-0933.2002.08.001 |
| [21] | 陕西省统计局, 国家统计局陕西调查总队. 陕西统计年鉴-2018[M]. 北京: 中国统计出版社, 2018: 18-19. |
| [22] |
王劲峰, 徐成东. 地理探测器: 原理与展望[J]. 地理学报, 2017, 72(1): 116-134. Wang J F, Xu C D. Geodetector: principle and prospective[J]. Acta Geographica Sinica, 2017, 72(1): 116-134. |
| [23] |
黄小刚, 赵景波, 孙从建, 等. 汾渭平原PM2.5空间分布的地形效应[J]. 环境科学, 2021, 42(10): 4582-4592. Huang X G, Zhao J B, Sun C J, et al. Orographic influences on the spatial distribution of PM2.5 on Fen-Wei Plain[J]. Environmental Science, 2021, 42(10): 4582-4592. |
| [24] | Wang J F, Li X H, Christakos G, et al. Geographical detectors-based health risk assessment and its application in the neural tube defects study of the Heshun region, China[J]. International Journal of Geographical Information Science, 2010, 24(1): 107-127. DOI:10.1080/13658810802443457 |
| [25] | Zhou Y, Li X H, Liu Y S. Land use change and driving factors in rural China during the period 1995-2015[J]. Land Use Policy, 2020, 99. DOI:10.1016/J.LANDUSEPOL.2020.105048 |
| [26] |
高煜, 王国兰, 金梓函, 等. 千河下游水体-沉积物重金属空间分布、风险及影响因素[J]. 环境科学, 2021, 42(11): 5333-5345. Gao Y, Wang G L, Jin Z H, et al. Spatial distribution, risk, and influencing factors of river water-sediment heavy metals in the lower reaches of the Qianhe River[J]. Environmental Science, 2021, 42(11): 5333-5345. |
| [27] |
黄小刚, 赵景波, 曹军骥, 等. 长江经济带PM2.5分布格局演变及其影响因素[J]. 环境科学, 2020, 41(3): 1013-1024. Huang X G, Zhao J B, Cao J J, et al. Evolution of the distribution of PM2.5 concentration in the Yangtze River economic belt and its influencing factors[J]. Environmental Science, 2020, 41(3): 1013-1024. |
| [28] |
杨伟, 姜晓丽. 华北地区大气细颗粒物(PM2.5)年际变化及其对土地利用/覆被变化的响应[J]. 环境科学, 2020, 41(7): 2995-3003. Yang W, Jiang X L. Interannual characteristics of fine particulate matter in North China and its relationship with land use and land cover change[J]. Environmental Science, 2020, 41(7): 2995-3003. DOI:10.3969/j.issn.1000-6923.2020.07.024 |
| [29] |
纪文君, 李曦, 李成学, 等. 基于全谱数据挖掘技术的土壤有机质高光谱预测建模研究[J]. 光谱学与光谱分析, 2012, 32(9): 2393-2398, 2408. Ji W J, Li X, Li C X, et al. Using different data mining algorithms to predict soil organic matter based on visible-near infrared spectroscopy[J]. Spectroscopy and Spectral Analysis, 2012, 32(9): 2393-2398, 2408. DOI:10.3964/j.issn.1000-0593(2012)09-2393-06 |
| [30] |
黄华, 李茂亿, 陈吟晖, 等. 基于PLSR的珠江口城市河流水质高光谱反演[J]. 水资源保护, 2021, 37(5): 36-42. Huang H, Li M Y, Chen Y H, et al. Water quality retrieval by hyperspectra for river in Pearl River Estuary city based on partial least squares regress[J]. Water Resources Protection, 2021, 37(5): 36-42. |
| [31] |
于雷, 洪永胜, 耿雷, 等. 基于偏最小二乘回归的土壤有机质含量高光谱估算[J]. 农业工程学报, 2015, 31(14): 103-109. Yu L, Hong Y S, Geng L, et al. Hyperspectral estimation of soil organic matter content based on partial least squares regression[J]. Transactions of the Chinese Society of Agricultural Engineering, 2015, 31(14): 103-109. DOI:10.11975/j.issn.1002-6819.2015.14.015 |
| [32] |
郭飞, 许镇, 马宏宏, 等. 基于PCA的土壤Cd含量高光谱反演模型对比研究[J]. 光谱学与光谱分析, 2021, 41(5): 1625-1630. Guo F, Xu Z, Ma H H, et al. A comparative study of the hyperspectral inversion models based on the PCA for retrieving the Cd content in the soil[J]. Spectroscopy and Spectral Analysis, 2021, 41(5): 1625-1630. |
| [33] |
阿依努尔·麦提努日, 麦麦提吐尔逊·艾则孜, 麦尔哈巴·图尔贡, 等. 吐鲁番盆地葡萄园土壤重金属铅含量高光谱估算[J]. 遥感技术与应用, 2021, 36(2): 362-371. Matnuri A, Eziz M, Turgun M, et al. Hyperspectral estimation of heavy metal Pb concentration in vineyard soil in Turpan Basin[J]. Remote Sensing Technology and Application, 2021, 36(2): 362-371. |
| [34] |
段丽君, 张海涛, 郭龙, 等. 典型柑橘种植区土壤有机质空间分布与含量预测[J]. 华中农业大学学报, 2019, 38(1): 73-81. Duan L J, Zhang H T, Guo L, et al. Spatial distribution and content prediction of soil organic matter in typical citrus growing areas[J]. Journal of Huazhong Agricultural University, 2019, 38(1): 73-81. |
| [35] |
韩杏杏, 陈杰, 王海洋, 等. 基于随机森林模型的耕地表层土壤有机质含量空间预测——以河南省辉县市为例[J]. 土壤, 2019, 51(1): 152-159. Han X X, Chen J, Wang H Y, et al. Spatial prediction of SOM content in topsoil based on random forest algorithm: a case study of Huixian City, Henan Province[J]. Soils, 2019, 51(1): 152-159. |
| [36] |
郭澎涛, 李茂芬, 罗微, 等. 基于多源环境变量和随机森林的橡胶园土壤全氮含量预测[J]. 农业工程学报, 2015, 31(5): 194-202. Guo P T, Li M F, Luo W, et al. Prediction of soil total nitrogen for rubber plantation at regional scale based on environmental variables and random forest approach[J]. Transactions of the Chinese Society of Agricultural Engineering, 2015, 31(5): 194-202. DOI:10.3969/j.issn.1002-6819.2015.05.028 |
| [37] |
卢宏亮, 赵明松, 刘斌寅, 等. 基于随机森林模型的安徽省土壤属性空间分布预测[J]. 土壤, 2019, 51(3): 602-608. Lu H L, Zhao M S, Liu B Y, et al. Spatial prediction of soil properties based on random forest model in Anhui Province[J]. Soils, 2019, 51(3): 602-608. |
| [38] | Breiman L. Random forest[J]. Machine Learning, 2001, 45(1): 5-32. DOI:10.1023/A:1010933404324 |
| [39] |
王玉娜, 李粉玲, 王伟东, 等. 基于无人机高光谱的冬小麦氮素营养监测[J]. 农业工程学报, 2020, 36(22): 31-39. Wang Y N, Li F L, Wang W D, et al. Monitoring of winter wheat nitrogen nutrition based on UAV hyperspectral images[J]. Transactions of the Chinese Society of Agricultural Engineering, 2020, 36(22): 31-39. DOI:10.11975/j.issn.1002-6819.2020.22.004 |
| [40] |
张万涛, 吉静怡, 李彬彬, 等. 黄土高原不同地貌区农田土壤有机质预测方法研究[J]. 植物营养与肥料学报, 2021, 27(4): 583-594. Zhang W T, Ji J Y, Li B B, et al. Spatial prediction of soil organic matter of farmlands under different landforms in the Loess Plateau, China[J]. Journal of Plant Nutrition and Fertilizers, 2021, 27(4): 583-594. |
| [41] |
李菊梅, 王朝辉, 李生秀. 有机质、全氮和可矿化氮在反映土壤供氮能力方面的意义[J]. 土壤学报, 2003, 40(2): 232-238. Li J M, Wang Z H, Li S X, et al. Significance of soil organic matter, total N and mineralizable nitrogen in reflecting soil N supplying capacity[J]. Acta Pedologica Sinica, 2003, 40(2): 232-238. DOI:10.3321/j.issn:0564-3929.2003.02.011 |
| [42] |
王琦, 常庆瑞, 黄勇, 等. 基于Geo-D的陕西省STN空间变异影响因子交互作用研究[J/OL]. 农业机械学报: 1-13. http://kns.cnki.net/kcms/detail/11.1964.S.20210322.1446.002.html, 2021-04-06. Wang Q, Chang Q R, Huang Y, et al. Driving factors and interaction of STN spatial variability in Shaanxi Province based on Geo-D[J/OL]. Transactions of the Chinese Society for Agricultural Machinery: 1-13. http://kns.cnki.net/kcms/detail/11.1964.S.20210322.1446.002.html, 2021-04-06. |
| [43] |
赵倩倩, 赵庚星, 董超, 等. 高密市农田土壤养分空间变异特征研究[J]. 土壤通报, 2012, 43(3): 643-650. Zhao Q Q, Zhao G X, Dong C, et al. Spatial variability of soil nutrients of cultivated land in Gaomi area[J]. Chinese Journal of Soil Science, 2012, 43(3): 643-650. |
| [44] |
赵云, 陈伟, 李春鸣, 等. 东祁连山不同退化程度高寒草甸土壤有机质含量及其与主要养分的关系[J]. 草业科学, 2009, 26(5): 20-25. Zhao Y, Chen W, Li C M, et al. Content of soil organic matter and its relationships with main nutrients on degraded alpine meadow in Eastern Qilian Mountains[J]. Pratacultural Science, 2009, 26(5): 20-25. DOI:10.3969/j.issn.1001-0629.2009.05.004 |
| [45] |
李梦佳, 王磊, 刘洪斌, 等. 不同模型预测土壤有机质含量空间分布对比分析[J]. 西南农业学报, 2021, 34(3): 610-617. Li M J, Wang L, Liu H B, et al. Contrastive analysis of spatial distribution of soil organic matter content predicted by different models[J]. Southwest China Journal of Agricultural Sciences, 2021, 34(3): 610-617. |
| [46] |
齐雁冰, 王茵茵, 陈洋, 等. 基于遥感与随机森林算法的陕西省土壤有机质空间预测[J]. 自然资源学报, 2017, 32(6): 1074-1086. Qi Y B, Wang Y Y, Chen Y, et al. Soil organic matter prediction based on remote sensing data and random forest model in Shaanxi Province[J]. Journal of Natural Resources, 2017, 32(6): 1074-1086. |
| [47] |
胡贵贵, 杨粉莉, 杨联安, 等. 基于主成分和机器学习的土壤有机质含量空间预测建模[J]. 干旱区地理, 2021, 44(4): 1114-1124. Hu G G, Yang F L, Yang L A, et al. Spatial prediction modeling of soil organic matter content based on principal components and machine learning[J]. Arid Land Geography, 2021, 44(4): 1114-1124. |
| [48] |
赵明松, 刘斌寅, 卢宏亮, 等. 基于地理加权回归的地形平缓区土壤有机质空间建模[J]. 农业工程学报, 2019, 35(20): 102-110. Zhao M S, Liu B Y, Lu H L, et al. Spatial modeling of soil organic matter over low relief areas based on geographically weighted regression[J]. Transactions of the Chinese Society of Agricultural Engineering, 2019, 35(20): 102-110. DOI:10.11975/j.issn.1002-6819.2019.20.013 |
| [49] |
唐海涛, 孟祥添, 苏循新, 等. 基于CARS算法的不同类型土壤有机质高光谱预测[J]. 农业工程学报, 2021, 37(2): 105-113. Tang H T, Meng X T, Su X X, et al. Hyperspectral prediction on soil organic matter of different types using CARS algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering, 2021, 37(2): 105-113. |
 2022, Vol. 43
2022, Vol. 43


