2. 广东省环境科学研究院, 广州 510045
2. Guangdong Provincial Academy of Environmental Science, Guangzhou 510045, China
土壤镉具有高毒性、易累积和难降解的特点, 随着食物链进入人体积累, 引发多种疾病, 严重威胁人体健康.土壤中的镉具有明显的空间异质性, 精准识别其空间分布对于土壤污染防治及农产品布局具有重要意义[1].土壤镉空间分布的影响因素有很多, 可概括为两类:一是自然因素, 主要包括成土母质[2]和土壤的理化性质(如pH和有机质含量)等; 二是人为因素, 主要包括土地利用类型[3]、工业污染[4]、交通排放[5]和农业生产等.有研究表明, 人类活动对重金属空间分布的影响已经远远超过自然背景. Gay等[6]的研究显示, 镉是土壤重金属污染的主要污染物, 污染成因复杂, 精准模拟其空间分布面临着巨大挑战[7].
空间插值法是模拟土壤重金属空间分布的重要手段.普通克里格(ordinary Kriging, OK)作为最简单有效的空间插值方法, 近年来应用较广[6], 但是, 该方法忽视了影响土壤重金属空间分布的环境要素, 其空间插值精度不高[8].通过构建回归克里格(regression Kriging, RK)模型, 利用OK与回归分析结合起来, 将影响插值变量的环境因子作为辅助变量, 建立插值变量与其影响因子之间的回归模型, 可以克服OK不足, 提高模拟精度[9].例如, Mondal等[10]的研究基于亮度指数、绿色指数和归一化植被指数等8个辅助变量的RK, 估算了印度纳尔默达河流域的土壤有机碳的空间分布.邵亚等[11]利用海拔高度、坡度和坡向等多个地理环境因子作为辅助数据, 构建了地理加权回归模型, 该方法比OK相关系数提升了59.38%.杨顺华等[12]的研究选取相对高程和汇流动力指数作为辅助变量构建模型, 发现RK法插值结果的平均误差、平均绝对误差和均方根误差相较于OK法分别降低39.2%、17.7%和20.6%.但是, 上述研究也存在一些问题, 例如未充分考虑土壤重金属复杂的来源和迁移转化过程, 特别是对于人为因素影响方面多只考虑土地利用, 缺乏对点状和线性等污染源的关注[13~15]; 此外, 环境要素之间的相关性会导致多重共线性问题, 降低回归函数的准确性[16].因此, 如何选取合适有效的环境变量, 去除各因素的自相关性是提升回归克里格模型模拟精度有效途径.
鉴于此, 本文从自然和人为两个方面选取23个影响因子, 应用主成分分析改进的回归克里格模型, 并考虑因子自相关性, 构建NRK(仅基于自然因子的回归克里格法)和NARK(基于自然-人为因子的回归克里格法)重金属空间分布模拟框架以南方某市冶炼厂周边区域为实证区域, 以期说明自然和人为因素对于区域土壤重金属分布模拟的影响.
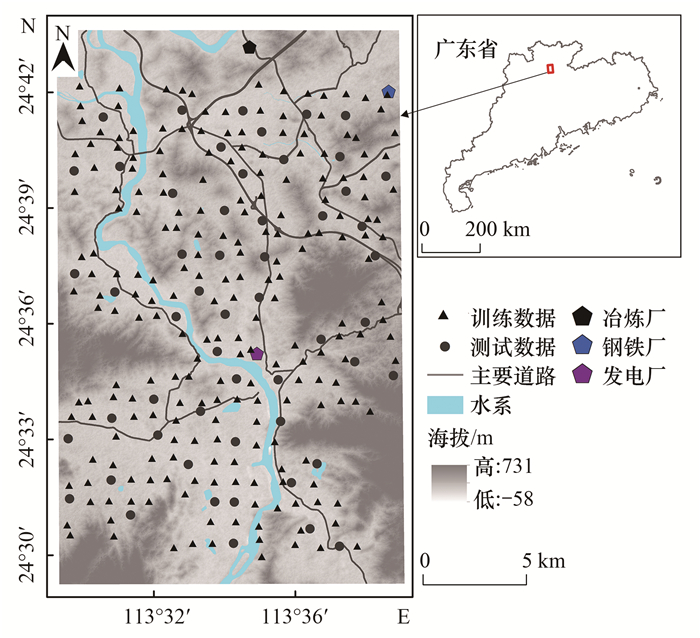
1 材料与方法 1.1 研究区概况研究区所在市是我国典型的重工业城市, 于20世纪五、六十年代先后建立了发电厂、冶炼厂和钢铁厂等大型重工业, 有色金属加工成为主导产业.伴随着工业和经济高速发展, 由于重金属加工和电镀等产业发展方式较为粗放, 早期污染物排放量较大, 土壤作为污染物的最终受体, 该区土壤重金属污染成为突出的问题, 王其枫等[17]和Dong等[18]的研究数据显示, 该地区土壤重金属镉污染情况严重.选取钢铁厂、冶炼厂和发电厂交汇区为重点研究区域(112°50′~114°45′E、23°5′~25°31′N), 聚焦重金属污染的时空分布.该区属亚热带季风气候, 盛行南北向风(图 1).
|
图 1 研究区域与样点分布示意 Fig. 1 Location of the study area and spatial distribution of the soil samples |
依据《土壤环境质量监测技术规范》(HJ/T 166-2004)要求, 综合考虑成土母质和土地利用的情况, 采用均匀布点和系统布点相结合的方法, 于2019年4月采集了271个点位土壤表层样品(0~20 cm).土壤样品采集后经自然风干, 去除杂物, 研磨过100目筛后, 采用HCl-HNO3-HF-HClO4法消解土壤样品, 经电感耦合等离子体光谱仪(ICP-OES, PerkinElmer Optima 8300, USA)测定镉元素.采用玻璃电极法测定土pH, 采用重铬酸钾氧化-分光光度法(HJ 615-2011)法测定土壤有机碳.分析过程中采用的试剂均为优级纯, 重金属的加标回收率为86.4%~110%之间, 同时进行空白试验, 测试的准确度和精密度符合国家一级标准物质GSS-4质量控制要求.使用全球定位系统(GPS)标记采样点位, 样点分布见图 1.
1.3 影响因素和数据处理 1.3.1 影响因素自然状态下, 成土母质是土壤镉的主要来源, 镉的活性和迁移速率受到土壤环境参数(酸碱度、有机质)、地形地貌和河流运移的影响.人为污染源是该市土壤镉的重要来源, 工业和交通布局对其空间分布影响很大.因此, 考虑到该区域土壤镉的多种来源, 且受自然和人为环境因素影响较大, 镉污染空间分布存在较大异质性特点, 综合选取了23个影响因素, 详见表 1.
|
|
表 1 土壤重金属镉空间分布影响因素 Table 1 Influencing factors used in this study |
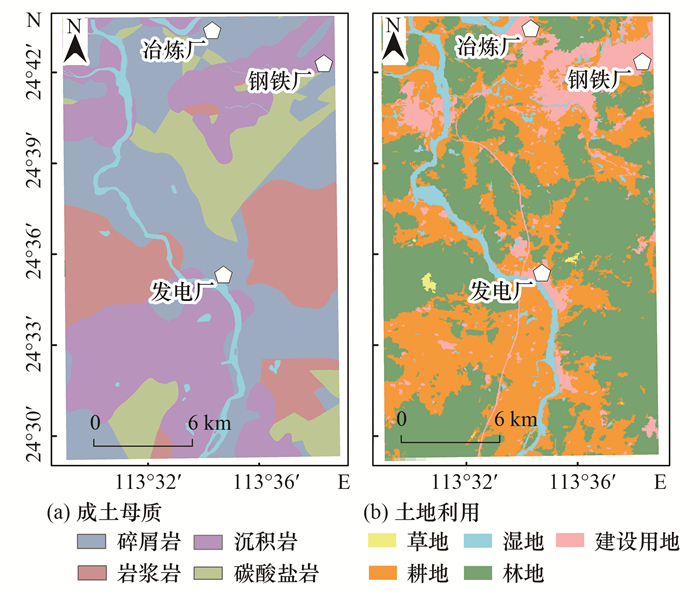
其中地形数据来自于地理空间数据云(http://www.gscloud.cn), 空间精度为30 m; 土地利用类型数据来源于地理资源与生态专业知识服务平台(网址), 分辨率为30 m; 取1:25万地质图来源于Local Space(图 2).风频数据来源于中国气象网多年统计数据(2015~2018年).成土母质和土地利用2个类型变量采用哑变量变换参与计算; 工业大气排放对样点的影响通过样点与企业的距离和样点相对工业企业风向上风频表达, 用FDi表示:
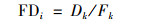
|
(1) |
|
图 2 研究区域成土母质和土地利用分布 Fig. 2 Distribution of land use and parent materials in the study |
式中, FDi是指不同样点受到工业企业的影响, 即工业企业影响因子; Fk是指样点位于工业企业风向上的风频; Dk是指样点距离工业企业的相邻距离; i为A、B和C分别表示发电厂、钢铁厂和冶炼厂.
1.3.2 模型构建利用SPSS 22.0的双变量相关分析、主成分分析、多元线性逐步回归和Origin 2020的方差分析功能, 结合Arcgis 10.2的空间分析功能, 分析土壤镉含量与环境变量之间的相关性; 通过分析土壤镉在不同类型变量上的显著性差异提取主要影响因素; 再利用主成分分析, 提取主控环境因子, 构建基于主成分的改进回归克里格模型(RK), 并将其与普通克里格模型(OK)进行对比.
为了对比分析自然因素、人为因素以及人为因素中的大气排放(考虑到大气排放是本区域重金属分布最为重要因素)对土壤中重金属空间模拟的影响, 构建了仅基于自然因子的回归克里格法(nature regression Kriging, NRK)、基于自然-人为因子的回归克里格法(natural anthropology regression Kriging, NARK)以及不考虑大气排放影响的回归克里格法(no atmospheric emission regression Kriging, NAERK)这种模型.
1.3.3 普通克里格普通克里格(OK)是一种常用的空间插值方法[19], 假设区域变量的平均值在整个研究区域中是未知常数.通过基于无偏预测和最小方差的半变异函数确定加权因子, 计算公式如下[20]:
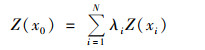
|
(2) |
式中, Z(x0)表示未知点的值, Z(xi)表示未知样点周围已知样本点的值, N表示已知样本点的个数, λi表示第i个样本点的权重.
1.3.4 利用主成分分析改进的回归克里格回归克里格模型中观测值被视为漂移和残差之和, 它是OK模型的扩展[21].漂移是由环境因素引起的综合影响, 通常使用多元线性回归进行拟合.残差在空间上是固定的, 理论上呈正态分布.因此, 在非采样位置X0处的预测值是回归测量的漂移与OK模型估计的残差和, 计算公式如下[22, 23]:
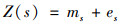
|
(3) |
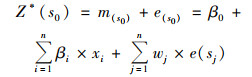
|
(4) |
式中, Z(s)是区域化变量的观测数据集; ms是相对应的漂移数据集; es是残差数据集.Z*(s0)是位置样点的预测值; βi是回归函数的回归系数; xi是独立变量; wj是普通克里格法的权重; e(sj)是样点sj处的残差.
有研究表明, 环境因子之间具有较强的相关性, 在回归中可能产生多重共线的问题[16].因此, 本文采用主成分分析和多元线性回归结合的方式建立回归方程[24].作为多变量分析方法, 最大方差旋转方法可以有效减少每个组件上的高负荷变量的数量[25], 取特征值大于1的主要成分(PCs, s=1, 2, …, n).在获得PC之后建立回归方程, 将多元线性回归方程应用到回归克里格中.
1.3.5 模型精度验证选择平均绝对误差(MAE), 均方根误差(RMSE)、测量值标准偏差与均方根误差的比值(RPD)和R2作为模型精度评价指标, R2越大, MAE和RMSE越小, 则模型精度越高[26], 当1.5≤RPD<2.0时表明模型只能进行粗略估计, 当2.0≤RPD<2.5时表明模型具有较好地预测能力, 当2.5≤RPD<3.0时表明模型具有很好地预测能力, 当RPD≥3.0时表明模型具有极好地预测能力[12].用RI表示两个模型之间预测精度的差异[27].
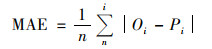
|
(5) |
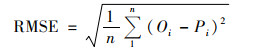
|
(6) |
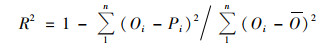
|
(7) |
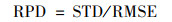
|
(8) |
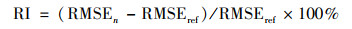
|
(9) |
式中, n是数量的样本, σi2样点克里格的方差, Oi是样点观测值, 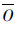
土壤镉含量介于0.07~21.93 mg·kg-1之间, 均值为3.55 mg·kg-1, 按照土壤质量环境标准(GB 15618-2018和GB 36600-2018)划分, 点位超标率达到85.93%, 土壤镉污染严重.从成土母质来看, 镉平均值分布:碳酸盐岩>碎屑岩>岩浆岩>沉积岩; 沉积岩中变异系数大于100%, 为强变异, 其他母质类型均为中等变异; 从土地利用类型来看, 镉平均值大小排序为:建设用地>草地>耕地>林地; 所有土地利用类型均呈现中等变异(表 2).
|
|
表 2 不同成土母质和土地利用类型的描述性统计 Table 2 Descriptive statistics of Cd by parent materials and land use types |
2.2 土壤镉含量与影响因素之间的相关性
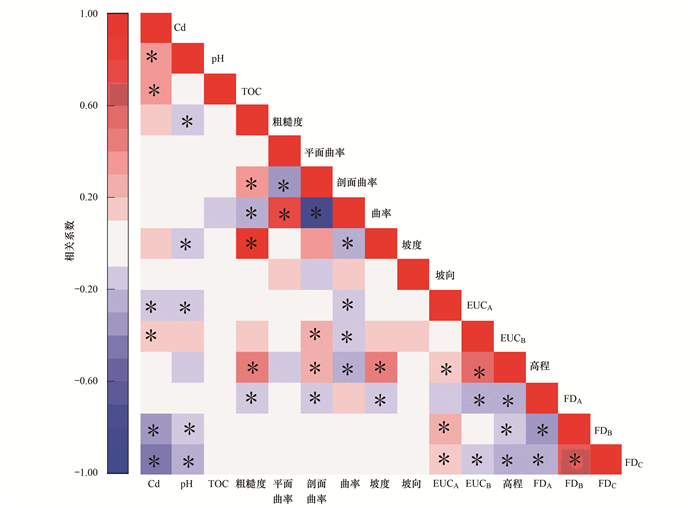
采用Spearman相关系数探讨土壤镉含量与环境因素之间的关系.结果显示, 河流和道路的欧氏距离、冶炼厂大气排放、钢铁厂大气排放、土壤有机质含量和土壤pH与镉含量呈显著相关(图 3), 各环境因素对土壤镉含量的影响程度由高到低呈现为冶炼厂大气排放>钢铁厂大气排放>pH>有机质>与道路的欧氏距离>与河流的欧氏距离.
|
FDA、FDB和FDC分别表示发电厂、钢铁厂和冶炼厂的工业大气排放影响; EUCA和EUCB:表示点位距离主要路网和河流的欧氏距离; *表示在0.05水平(双侧)上显著相关 图 3 镉含量与影响因素的Spearman相关性 Fig. 3 Spearman's correlation coefficients between Cd and the influential factors |
为避免自然影响因素之间较强的相关性(图 3)导致多元线性拟合过程出现较大的共线性, 采用主成分分析法处理数据.经KMO检验值为0.675, 大于0.5, 球形度检验P为0.017, 小于0.05, 表明可采用主成分分析.采用最大方差旋转PCA, 选取特征值大于1的6个PCs(s=1, 2, 3, 4, 5, 6), 成分矩阵见表 3, 用于多元线性逐步回归方程.选用的6个PC可以解释总方差分别为23.68%、37.87%、48.86%、58.88%、67.54%和75.23%(表 3).将成土母质和土地利用被转换成虚拟变量纳入计算[28].以逐步回归的多元线性函数来量化土壤镉含量与不同变量之间的关系, 逐步回归法每引入一个自变量都将对已输入的变量进行F检验, 以确保回归方程中只包含显著变量, 表 4列出了土壤镉含量与不同变量的系数和回归函数的决定系数R2.从中可知, NARK模型中的回归函数R2最高, 解释能力最佳.
|
|
表 3 自然因素的主成分分析矩阵1) Table 3 Principal component analysis matrix of natural factors |
|
|
表 4 不同模型关于变量的回归系数1) Table 4 Regression coefficients of the different models on variables |
对多元线性函数的残差进行K-S检验, 用拉伊达法则(平均值±标准差)在剔除异常值后, 在显著性水平为0.05时符合正态分布假设(H0).通过GS+ 9.0软件根据函数的最高R2和最低残差平方和的原理, 确定OK、NRK残差和NARK残差的最佳拟合半变异函数, 其参数如表 5所示.根据块金效应的划分, 块基比<25%为强空间变异, 25%~75%为中等空间变异, >75%为弱空间变异[29], OK模型、NRK模型和NAERK模型的块金效应呈现中等空间变异, NARK模型残差呈现强空间变异, NARK模型的空间依赖性最强.NARK模型空间自相关范围为14.7 km, 显著高于前3种模型.
|
|
表 5 利用不同类型影响因子4种模型的半方差函数和参数 Table 5 Semi-variograms and parameters of the four models |
2.4 模型验证
应用Arcgis软件中的地统计分析模块基于随机性原则分别选取217和54个样本作为测试集和验证集, 各占样本比例为80%和20%[10].验证效果表明(表 6):NARK是4种模型中MAE和RMSE最小, R2和RPD最大的, 说明结合人为因素和自然因素的回归克里格的模拟效果最好.没有利用辅助因素的OK模型只能粗略估计土壤镉空间分布情况, 而仅利用自然因素的NRK模型和没有考虑大气排放的NAERK模型的RPD分别为2.02和2.17, 两个模型都具有较好地预测能力, 利用自然和人为因素的NARK模型具有很好地预测能力.NRK模型较OK模型的MAE和RMSE分别降低4.15%和8.35%, RPD提升了9.12%;不考虑大气排放的NAERK模型较OK模型的MAE和RMSE降低了10.93%和17.61%, RPD提升了21.38%;融合了自然和人为因素的NARK模型较OK模型的MAE和RMSE分别降低27.30%和30.56%, RPD提升了44.01%.以上结果说明合理地利用多源辅助数据有利于提升改进回归克里格模型预测效果, 对大气污染源周边大气点源排放对该区域土壤镉空间模拟的精度提升有至关重要的作用.
|
|
表 6 不同影响因素对模型精度的影响 Table 6 Influence of the different influence factors on the precision of the models |
2.5 土壤镉空间模拟结果比较
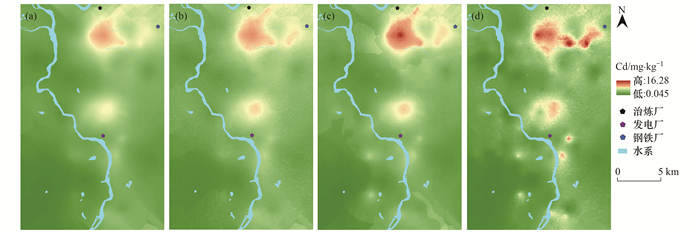
从空间分布可以看出(图 4), 通过4种不同方法模拟的土壤镉含量空间分布呈现了相似的空间分布, 均出现了两个高值区域, 高低值的变化趋势也是相同的.但是, 4种方法在局部有明显差异, 前3种模型的空间分布更为接近, 高值区域相对集中且位置相同, 增加了大气点源排放影响NARK模型出现多个高值区域且较为分散.首先OK法的模拟结果在空间上分布差异较小, 模拟结果更为平滑, 高值区域的镉含量相对较低, 捕捉到的局部异质性信息较少, 其拟合结果范围为0.12~11.05mg·kg-1, 预测结果范围较小, 与实测值范围(0.07~21.93mg·kg-1)差异最大.其中NRK模型与OK模型空间分布没有很大的区别, 其拟合结果范围为0.10~15.32 mg·kg-1, 较OK模型有小幅度扩大, 但是空间分布仍然十分平滑, 高值区域没有明显的边界.辅助因素增加了土地利用和主要交通干道后, NAERK模型在空间上出现明显的块状高值区域, 高值区域相对集中, 界线清晰, 出现了明显的斑块状分布, 在一定程度上克服了克里格的平滑效应, 但是小范围的空间异质性仍然没有得到明显地体现, 其拟合结果范围为0.08~16.37mg·kg-1.NARK应用了自然因素和人为因素作为辅助数据, 捕捉到的局部信息相对较多, 空间分布预测结果与其他3种模型有明显区别, 其空间分布较为突兀, 高低值呈斑块分布且较为离散, 体现了原始数据的波动性, 其拟合结果范围为0.045~19.68mg·kg-1, 与原始数据范围最为接近.
|
(a)普通克里格(OK); (b)基于自然因素的回归克里格(NRK); (c)没有大气点源污染的回归克里格(NAERK); (d)基于自然和人为因素的回归克里格(NARK) 图 4 不同影响因素对空间分布的影响 Fig. 4 Influence of different factors on the spatial distribution |
本研究选取的部分指标与土壤镉含量显著相关.对于自然因素来说, 土壤pH和有机碳含量与土壤镉含量呈正相关, 表明碱性土壤和高有机碳含量土壤有助于土壤中重金属的累积.由于pH会影响土壤镉的迁移转化能力, 在pH较低的酸性土壤中, H+使镉离子从土壤颗粒中解吸出来, 从而增加了镉的活性和迁移转化能力[16].有机碳含量是影响表层土壤镉含量的重要影响因素, 其可能是土壤中的有机质与其他物质相结合形成胶体, 增大了土壤的表面积和表面活性, 因此土壤吸附镉的能力随之增大, 这与李树辉等[30]的研究发现, 菜地中土壤镉的含量与土壤有机碳呈正相关的结果一致.河流两岸为河流冲积物, 受流水运输和泥沙吸附影响, 河流冲积物土壤重金属含量本应相对较高, 但是在本研究区域中样点距离河流的欧氏距离与土壤镉含量呈正相关[31], 这可能是因为土壤镉主要来源于工业污染源, 工业区距离河岸较远[32].由于受到包括施肥、金属冶炼和大气扬尘等多种人为随机因素的影响, 土壤镉含量在局部呈突变趋势[33].NRK模型仅在利用自然因素建立模型, 空间分布趋势与OK模型结果相近, 整体空间变化平缓, 高值区域面积相对扩大, 模型精度虽有小幅度的提升, 但是空间突变刻画效果不佳, 与土壤Cd实际分布存在较大差异.这表明, 经过主成分分析提取的自然因素信息对研究区高值区域的模拟效果有所提升, 但是提升幅度有限, 自然因素不是本研究区土壤Cd含量空间分布的主控因素.
对于人为因素来说, 土壤镉含量与样点距离道路和工业企业的距离呈显著负相关.这表明汽车汽油燃烧和含镉的汽车轮胎磨损过程排放的镉污染也是一个重要的污染源[5].经过主成分分析提取自然和人为因素信息后, NARK模型模拟效果出现明显提升, 土壤Cd空间分布出现明显的突变趋势, 模拟精度R2达到最高.高值区域面积小且较为分散, 较好地反映了原始数据的波动性.南部地区出现多个高值区域, 空间模拟的高值区与重点污染源所在位置并不完全匹配, 这可能是因为钢铁厂的南部、发电厂东南部和发电厂西部地形起伏较大, 工业废气排放扩散过程中, 污染物受风和地形综合影响, 局部高山形成涡流, 导致污染物运移受阻, 下沉至地面[34~36].本区域工业废气是以高架烟囱形式排放, 基本符合稳定连续点源排放, 大气污染物沉降也基本符合高架连续点源大气扩散模型分布特征, 即在污染企业周边其大气沉降浓度趋近于零, 之后一定范围内污染物浓度与距工业企业的距离正相关, 出现峰值后浓度下降[37~40].
许多研究将高程、坡度、汇聚指数和有机质含量等自然因素作为辅助变量优化土壤重金属空间分布模型, 结果表明自然因素对土壤重金属空间分布模型的优化是有限的.例如, Song等[27]利用高程、坡度和地形湿度指数等18个自然影响因素预测土壤中重金属空间分布, 砷、镉、铬、铅和锌的R2分别为0.642、0.618、0.544、0.609和0.593, 其拟合结果空间分布平滑, 没有明显的边界, 说明模型拟合精度仍然有待提高.李润林等[41]分别以土壤有机质、pH、全氮、碱解氮、有效铁、有效铜、有效锰和高程数据为辅助变量, 采用协同克里格插值方法预测土壤中锌含量空间分布, 结果表明其较普通克里格仅有小幅度提升.在中小尺度上, 土壤重金属含量可能会受到人为影响的作用更大.本文中相关性分析发现土壤镉含量与人为因素的相关系数大于自然影响因素, 不同的耕作方式和施肥影响了土壤镉含量的空间分布, 且研究区内存在电厂和冶炼厂等都是重要污染源, 这些人为因素成为区域土壤镉的主要输入源头.因此, 根据研究区域不同, 综合考虑自然-人为等多源辅助变量的RK模型, 可以有效提升土壤重金属空间分布预测精度.
3.2 改进的回归克里格模型对预测精度的影响本研究利用主成分分析改进的回归克里格模型对土壤镉空间分布具有较好的模拟效果, 主要原因可能是土壤Cd受到研究区内地形地貌差异的影响较小, 受到土地利用方式和工业生产活动等随机因素带来的影响较大, 因此土壤镉变异特征在整个区域的空间上存在较大差异, 这不满足克里格方法的固定假设[42].在不满足固定假设的情况下, 根据样本实测数据得到的半方差函数并不是无偏估计, 基于半方差函数得到的加权因子会出现较大偏差, 使得OK模型预测精度不高.本研究利用OK方法模拟的空间分布图, 整体变化趋势平缓, 高值区域边界模糊, 只能粗略地估计污染较为严重的区域分布.这主要是因为土壤重金属含量与多源辅助数据之间呈现复杂的非线性关系[43], 简单的线性拟合会破坏土壤重金属固有的空间结构关系.传统的RK模型仅仅采用了多元线性回归计算土壤镉含量在空间上存在的漂移, 预测效果较差.影响土壤镉的环境因素之间多存在相关性, 利用主成分分析方法可以有效去除影响因素之间的重叠信息, 有利于寻找土壤镉含量与影响因素之间的量化关系[44].本文通过主成分分析法量化了系统内的漂移后, 回归的残差在空间上呈现平稳和正态分布[22], 取得了很好地模拟效果.在本研究中, 利用主成分分析方法改进的回归克里格方法模拟结果呈现明显的空间突变, 真实地反映了原始数据的波动性, 模拟效果达到最优.
4 结论(1) 研究区土壤Cd污染严重, 点位超标率达到85.93%, 土壤镉含量介于0.07~21.93mg·kg-1之间, 均值为3.55 mg·kg-1; 各环境因素对土壤镉含量的影响效果由大到小是:冶炼厂大气排放>钢铁厂大气排放>pH>有机质>与道路的欧氏距离>与河流的欧氏距离.
(2) 综合自然-人为因子改进回归克里格模型可以系统提取预测辅助变量, 极大提高了土壤镉预测精度, MAE和RMSE分别达到0.47和0.89, 较OK法分别降低了26.86%和30.56%; R2达到0.88, 比普通克里格法提升了0.1.工业污染源对该地区土壤镉模拟精度影响很大, 开展工业污染源的普查, 是支撑精准识别镉空间分布的重要工作基础.
| [1] | Sun L, Guo D K, Liu K, et al. Levels, sources, and spatial distribution of heavy metals in soils from a typical coal industrial city of Tangshan, China[J]. CATENA, 2019, 175: 101-109. |
| [2] | Wang S, Cai L M, Wen H H, et al. Spatial distribution and source apportionment of heavy metals in soil from a typical county-level city of Guangdong Province, China[J]. Science of the Total Environment, 2019, 655: 92-101. |
| [3] |
舒心, 李艳, 李锋, 等. 土壤重金属累积对土地利用与景观格局的响应[J]. 环境科学, 2019, 40(5): 2471-2482. Shu X, Li Y, Li F, et al. Impacts of land use and landscape patterns on heavy metal accumulation in soil[J]. Environmental Science, 2019, 40(5): 2471-2482. |
| [4] |
李艳玲, 卢一富, 陈卫平, 等. 工业城市农田土壤重金属时空变异及来源解析[J]. 环境科学, 2020, 41(3): 1432-1439. Li Y L, Lu Y F, Chen W P, et al. Spatial-temporal variation and source change of heavy metals in the cropland soil in the industrial city[J]. Environmental Science, 2020, 41(3): 1432-1439. |
| [5] | Leroy M C, Marcotte S, Legras M, et al. Influence of the vegetative cover on the fate of trace metals in retention systems simulating roadside infiltration swales[J]. Science of the Total Environment, 2017, 580: 482-490. |
| [6] | Gay J R, Korre A. Accounting for pH heterogeneity and variability in modelling human health risks from cadmium in contaminated land[J]. Science of the Total Environment, 2009, 407(14): 4231-4237. |
| [7] | El Khodrani N, Omrania S, Zouahri A, et al. Spatial distribution and mapping of heavy metals in agricultural soils of the Sfafaa region (Gharb, Morocco)[J]. Materials Today: Proceedings, 2019, 13: 832-840. |
| [8] |
罗梅, 郭龙, 张海涛, 等. 基于环境变量的中国土壤有机碳空间分布特征[J]. 土壤学报, 2020, 57(1): 48-59. Luo M, Guo L, Zhang H T, et al. Characterization of spatial distribution of soil organic carbon in China based on environmental variables[J]. Acta Pedologica Sinica, 2020, 57(1): 48-59. |
| [9] | Pásztor L, Szabó K Z, Szatmári G, et al. Mapping geogenic radon potential by regression kriging[J]. Science of the Total Environment, 2016, 544: 883-891. |
| [10] | Mondal A, Khare D, Kundu S, et al. Spatial Soil Organic Carbon (SOC) prediction by regression kriging using remote sensing data[J]. The Egyptian Journal of Remote Sensing and Space Science, 2017, 20(1): 61-70. |
| [11] |
邵亚, 王毅伟, 蔡崇法, 等. 西南典型岩溶区土壤硒空间分布预测[J]. 农业工程学报, 2016, 32(22): 178-183. Shao Y, Wang Y W, Cai C F, et al. Prediction on spatial distribution of soil selenium in typical karst area of Southwest China[J]. Transactions of the Chinese Society of Agricultural Engineering, 2016, 32(22): 178-183. |
| [12] |
杨顺华, 张海涛, 郭龙, 等. 基于回归和地理加权回归Kriging的土壤有机质空间插值[J]. 应用生态学报, 2015, 26(6): 1649-1656. Yang S H, Zhang H T, Guo L, et al. Spatial interpolation of soil organic matter using regression Kriging and geographically weighted regression Kriging[J]. Chinese Journal of Applied Ecology, 2015, 26(6): 1649-1656. |
| [13] | Lv J S, Liu Y, Zhang Z L, et al. Factorial kriging and stepwise regression approach to identify environmental factors influencing spatial multi-scale variability of heavy metals in soils[J]. Journal of Hazardous Materials, 2013, 261: 387-397. |
| [14] |
李春芳, 曹见飞, 吕建树, 等. 不同土地利用类型土壤重金属生态风险与人体健康风险[J]. 环境科学, 2018, 39(12): 5628-5638. Li C F, Cao J F, Lü J S, et al. Ecological risk assessment of soil heavy metals for different types of land use and evaluation of human health[J]. Environmental Science, 2018, 39(12): 5628-5638. |
| [15] |
李春芳, 王菲, 曹文涛, 等. 龙口市污水灌溉区农田重金属来源、空间分布及污染评价[J]. 环境科学, 2017, 38(3): 1018-1027. Li C F, Wang F, Cao W T, et al. Source analysis, spatial distribution and pollution assessment of heavy metals in sewage irrigation area farmland soils of Longkou city[J]. Environmental Science, 2017, 38(3): 1018-1027. |
| [16] |
李雨, 韩平, 任东, 等. 基于地理探测器的农田土壤重金属影响因子分析[J]. 中国农业科学, 2017, 50(21): 4138-4148. Li Y, Han P, Ren D, et al. Influence factor analysis of farmland soil heavy metal based on the geographical detector[J]. Scientia Agricultura Sinica, 2017, 50(21): 4138-4148. |
| [17] |
王其枫, 王富华, 孙芳芳, 等. 广东韶关主要矿区周边农田土壤铅、镉的形态分布及生物有效性研究[J]. 农业环境科学学报, 2012, 31(6): 1097-1103. Wang Q F, Wang F H, Sun F F, et al. Fractionation and bioavailability of Pb and Cd in agricultural soils around mining area in Shaoguan Guangdong province, China[J]. Journal of Agro-Environment Science, 2012, 31(6): 1097-1103. |
| [18] | Dong X Q, Li C L, Li J, et al. A novel approach for soil contamination assessment from heavy metal pollution: a linkage between discharge and adsorption[J]. Journal of Hazardous Materials, 2010, 175(1-3): 1022-1030. |
| [19] | Pajak M, Halecki W, Gąsiorek M. Accumulative response of Scots pine (Pinus sylvestris L.) and silver birch (Betula pendula Roth) to heavy metals enhanced by Pb-Zn ore mining and processing plants: explicitly spatial considerations of ordinary kriging based on a GIS approach[J]. Chemosphere, 2017, 168: 851-859. |
| [20] | Dai F Q, Zhou Q G, Lv Z Q, et al. Spatial prediction of soil organic matter content integrating artificial neural network and ordinary kriging in Tibetan Plateau[J]. Ecological Indicators, 2014, 45: 184-194. |
| [21] | Ye H C, Huang W J, Huang S Y, et al. Effects of different sampling densities on geographically weighted regression kriging for predicting soil organic carbon[J]. Spatial Statistics, 2017, 20: 76-91. |
| [22] | Giustini F, Ciotoli G, Rinaldini A, et al. Mapping the geogenic radon potential and radon risk by using Empirical Bayesian Kriging regression: a case study from a volcanic area of central Italy[J]. Science of the Total Environment, 2019, 661: 449-464. |
| [23] | Hengl T, Heuvelink G B M, Stein A. A generic framework for spatial prediction of soil variables based on regression-kriging[J]. Geoderma, 2004, 120(1-2): 75-93. |
| [24] | Guillén-Casla V, Rosales-Conrado N, León-González M E, et al. Principal Component Analysis (PCA) and Multiple Linear Regression (MLR) statistical tools to evaluate the effect of E-beam irradiation on ready-to-eat food[J]. Journal of Food Composition and Analysis, 2011, 24(3): 456-464. |
| [25] | 徐尚平, 陶澍, 徐福留, 等. 内蒙土壤微量元素含量的空间结构特征[J]. 地理学报, 2000, 55(3): 337-345. |
| [26] | Sun X L, Wu Y J, Zhang C S, et al. Performance of median kriging with robust estimators of the variogram in outlier identification and spatial prediction for soil pollution at a field scale[J]. Science of the Total Environment, 2019, 666: 902-914. |
| [27] | Song Y Q, Zhu A X, Cui X S, et al. Spatial variability of selected metals using auxiliary variables in agricultural soils[J]. CATENA, 2019, 174: 499-513. |
| [28] | Martin M P, Orton T G, Lacarce E, et al. Evaluation of modelling approaches for predicting the spatial distribution of soil organic carbon stocks at the national scale[J]. Geoderma, 2014, 223-225: 97-107. |
| [29] | Zhang S W, Shen C Y, Chen X Y, et al. Spatial interpolation of soil texture using compositional Kriging and regression Kriging with consideration of the characteristics of compositional data and environment variables[J]. Journal of Integrative Agriculture, 2013, 12(9): 1673-1683. |
| [30] |
李树辉, 曾希柏, 李莲芳, 等. 设施菜地重金属的剖面分布特征[J]. 应用生态学报, 2010, 21(9): 2397-2402. Li S H, Zeng X B, Li L F, et al. Distribution characteristics of heavy metals in soil profile of facility vegetable fields[J]. Chinese Journal of Applied Ecology, 2010, 21(9): 2397-2402. |
| [31] |
朱爱萍, 陈建耀, 高磊, 等. 北江上游水环境重金属污染及生态毒性的时空变化[J]. 环境科学学报, 2015, 35(8): 2487-2496. Zhu A P, Chen J Y, Gao L, et al. Spatial and temporal variation of heavy metals and their association with ecotoxicity in the upper reaches of Wengjiang river in Beijiang Basin[J]. Acta Scientiae Circumstantiae, 2015, 35(8): 2487-2496. |
| [32] | 初娜, 赵元艺, 张光弟, 等. 江西省德兴铜矿矿区重金属元素的环境效应[J]. 地质学报, 2008, 82(4): 562-576. |
| [33] |
王洋洋, 李方方, 王笑阳, 等. 铅锌冶炼厂周边农田土壤重金属污染空间分布特征及风险评估[J]. 环境科学, 2019, 40(1): 437-444. Wang Y Y, Li F F, Wang X Y, et al. Spatial distribution and risk assessment of heavy metal contamination in surface farmland soil around a lead and zinc smelter[J]. Environmental Science, 2019, 40(1): 437-444. |
| [34] |
谢南洪, 仝纪龙, 刘明, 等. 地表参数设置对高架点源大气污染物扩散预测的影响研究[J]. 环境科学与管理, 2017, 42(4): 32-36. Xie N H, Tong J L, Liu M, et al. Study on effect of surface parameter setting on air pollutant diffusion prediction in elevated point source[J]. Environmental Science and Management, 2017, 42(4): 32-36. |
| [35] |
李山泉, 杨金玲, 阮心玲, 等. 南京市大气沉降中重金属特征及对土壤环境的影响[J]. 中国环境科学, 2014, 34(1): 22-29. Li S Q, Yang J L, Ruan X L, et al. Atmospheric deposition of heavy metals and their impacts on soil environmentin in typical urban areas of Nanjing[J]. China Environmental Science, 2014, 34(1): 22-29. |
| [36] |
罗莹华. 韶关某冶炼厂周边土壤重金属污染调查与生态风险评价[J]. 安徽农业科学, 2016, 44(19): 133-136. Luo Y H. Investigation of soil pollution from heavy metals and assessment of its ecological risk around a smelting plant in Shaoguan[J]. Journal of Anhui Agricultural Sciences, 2016, 44(19): 133-136. |
| [37] | 郭尚其, 周洁军, 农泽喜. 广西某铅锌矿水文地质调查与重金属迁移规律研究[J]. 矿产与地质, 2019, 33(3): 567-572. |
| [38] | Yuan G L, Sun T H, Han P, et al. Environmental geochemical mapping and multivariate geostatistical analysis of heavy metals in topsoils of a closed steel smelter: capital iron & steel factory, Beijing, China[J]. Journal of Geochemical Exploration, 2013, 130: 15-21. |
| [39] | Liu J, Wang J, Xiao T F, et al. Geochemical dispersal of thallium and accompanying metals in sediment profiles from a smelter-impacted area in South China[J]. Applied Geochemistry, 2018, 88: 239-246. |
| [40] |
杨伟光, 王美娥, 陈卫平. 新疆干旱区某矿冶场对周围土壤重金属累积的影响[J]. 环境科学, 2019, 40(1): 445-452. Yang W G, Wang M E, Chen W P. Effect of a mining and smelting plant on the accumulation of heavy metals in soils in arid areas in Xinjiang[J]. Environmental Science, 2019, 40(1): 445-452. |
| [41] | 李润林, 姚艳敏, 唐鹏钦, 等. 县域耕地土壤锌含量的协同克里格插值及采样数量优化[J]. 土壤通报, 2013, 44(4): 830-838. |
| [42] | 韩杏杏, 陈杰, 王海洋, 等. 基于随机森林模型的耕地表层土壤有机质含量空间预测——以河南省辉县市为例[J]. 土壤, 2019, 51(1): 152-159. |
| [43] |
吴健生, 谢舞丹, 李嘉诚. 土地利用回归模型在大气污染时空分异研究中的应用[J]. 环境科学, 2016, 37(2): 413-419. Wu J S, Xie W D, Li J C. Application of land-use regression models in spatial-temporal differentiation of air pollution[J]. Environmental Science, 2016, 37(2): 413-419. |
| [44] | Keskin H, Grunwald S. Regression Kriging as a workhorse in the digital soil mapper's toolbox[J]. Geoderma, 2018, 326: 22-41. |
 2021, Vol. 42
2021, Vol. 42


