2. 中国科学院南京地理与湖泊研究所湖泊与环境国家重点实验室, 南京 210008;
3. 南京师范大学地理科学学院, 南京 210023;
4. 河南农业大学资源与环境学院, 郑州 450002
2. State Key Laboratory of Lake Science and Environment, Nanjing Institute of Geography and Limnology, Chinese Academy of Sciences, Nanjing 210008, China;
3. School of Geography Science, Nanjing Normal University, Nanjing 210023, China;
4. College of Resources and Environmental Sciences, Henan Agricultural University, Zhengzhou 450002, China
水体富营养化是当今水环境面临的重要威胁之一, 也是当下学术界研究的热点问题之一.就内陆二类水体而言, 水体富营养化不仅影响城市生态景观, 而且对人们休闲娱乐生活造成影响, 甚至对人类身体健康造成威胁[1, 2].遥感技术的快速发展, 突破了传统的水体监测方法的局限性, 实现了大面积区域的同步、长期、快速、动态监测, 已逐步成为水环境质量监测的一种重要手段[3~5].近年来, 随着遥感技术的不断发展和监测需求的不断提升, 越来越多的水色遥感传感器被投入使用.近年来, 有大量的水色要素估算模型被成功应用于海洋和内陆水环境监测, 极大地丰富和推动了多传感器在水环境监测中的应用[6~11].
相比于开阔大洋一类水体而言, 内陆二类水体光学特性复杂, 水色要素的精确估算往往对传感器波段设置有较高要求[6, 7].多光谱卫星传感器的波段设置往往难以覆盖模型所需求的所有波段, 这也成为限制内陆水环境遥感发展的一大瓶颈[4, 12].有学者针对这一问题, 利用多元线性回归模型进行了水体遥感反射率高光谱重构的研究[12~14].由于这种统计方法需要大量实测数据进行率定, 才能得到较高的模型精度.因此, 该算法对数据和研究区具有一定依赖性, 不易推广使用.
稀疏表达是近年来在信号处理领域广受关注的热点理论[15~17].稀疏表达是对原始信号在过完备字典上进行分解, 获得信号稀疏表示的一种方法.对于自然图像(RGB图像)、遥感多光谱或高光谱数据而言, 这些数据被为是稀疏信号[18].所以, 利用光谱数据的稀疏特性, 稀疏表达方法在图像融合[19, 20]、超分辨率图像重构[17]、图像去噪[21]、分类[22]和去云[23]等多方面得到了广泛的应用和推广.
本文基于稀疏表达方法, 提出一种新的水体遥感反射率高光谱重构方法, 利用水体光谱信号的稀疏性, 结合水体辐射传输模型理论上的普适性, 构建出具有高精度、高普适性的水体高光谱遥感反射率, 以期为内陆水环境遥感监测提供更好的数据源.
1 材料与方法 1.1 研究区与采样点分布太湖, 中国第三大淡水湖泊, 位于江苏省南部和浙江省北部交界处, 在航运、旅游、文化服务及生态服务等方面具有重要作用[6]. 2013年5月13日、2013年8月1~3日在太湖进行了水体遥感实验(图 1), 分别获取10个和39个样点的遥感反射率及叶绿素a和总悬浮物浓度数据.

|
图 1 研究区及采样点空间分布示意 Fig. 1 Locations of Lake Taihu and Hangzhou Bay and spatial distribution of the sampling sites |
杭州湾地处经济发达的长三角地区, 位于浙江省和上海市之间.西起浙江省海盐市澉浦镇和慈溪市之间的西三丰收闸断面, 与钱塘江水域为界; 东至上海扬子角-宁波镇海连线, 与舟山、北仑港海域为邻.杭州湾是世界上著名的强潮型海湾, 水动力条件复杂, 水体中悬浮颗粒物浓度具有含量高、浓度变化范围广及动态性强的特点[24]. 2017年7月22~24日在杭州湾进行水体遥感实验(图 1), 共获取50个样点的水体遥感反射率和总悬浮物浓度数据.
1.2 水质参数、遥感反射率测量及影像数据处理叶绿素a浓度的测定方法为常规化学分析法, 首先使用0.45 μm的Whatman GF/F滤膜进行过滤, 然后用90%的热乙醇萃取, 最后利用分光光度计进行分析计算, 详细测量方法参考文献[25].悬浮物浓度采用常规的干燥、烘烧、称重法(GB/T 11901-1989)测定.
水体遥感反射率光谱测量采用美国ASD公司生产的ASD FieldSpec Pro便携式光谱辐射计, 其波段范围为350~1 050 nm.测量方法采用唐军武等[26]提出的内陆二类水体水面以上光谱测量的方法.
为验证本研究所提出的高光谱重构算法的适用性, 获取了2013年5月13日以及2017年7月23日的同步GOCI影像数据. GOCI数据预处理包括几何校正、辐射定标和大气校正3个部分.其中, GOCI影像的几何校正通过其自带的经纬度网格, 在ENVI软件中进行校正; 辐射定标是通过GOCI数据头文件中的辐射定标参数在ENVI软件中完成; 大气校正使用6S模型进行校正[27].
1.3 稀疏表达重构算法水体遥感反射率的光谱信息是不同水体组分在不同浓度配比下的一种表现方式, 水体复杂的光谱信息本质上蕴含在水体辐射传输模型中.水体辐射传输模型是研究水体光学特征的重要机理模型, 理论上具有一定的普适性.因此, 本研究结合水体辐射传输模型来模拟水体遥感反射率光谱特征, 运用稀疏表达方法, 实现对水体遥感反射率的高光谱重构.重构方法主要包含以下步骤(图 2):首先, 利用水体生物光学模型, 模拟在不同水体组分配比条件下的水体高光谱遥感反射率及与传感器对应的多光谱遥感反射率, 分别生成高光谱冗余字典和多光谱冗余字典; 其次, 利用多光谱冗余字典对测量得到的多光谱数据进行分解, 获得多光谱稀疏系数; 最后, 用分解得到的多光谱稀疏系数和高光谱冗余字典, 重构得到高光谱数据.本研究中的实测多光谱数据是由实测高光谱数据根据不同多光谱传感器的波段响应函数重采样得到.

|
图 2 基于稀疏表达的高光谱重构算法流程示意 Fig. 2 Flowchart of the hyperspectral reconstruction algorithm based on sparse representation |
Lee等[28]的研究结果表明, 水面以上遥感反射率(Rrs)与水面以下遥感反射率(rrs)之间的关系可以表示为:
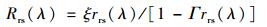
|
(1) |
式中, λ为波长(nm), ξ为离散作用系数, Γ为气水界面折射系数.在天顶观测时, ξ取值为0.52, Γ取值为1.7[29]. rrs可以表示为:
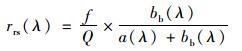
|
(2) |
式中, f为常数, 取值范围在0.2~0.56之间[30]; Q为依赖于水体光场分布的参数, 一般取值范围在1.7~7之间[30]. a为水体总的吸收系数(m-1), bb为水体总的后向散射系数(m-1). a和bb分别可以表示为水体各组分吸收系数和后向散射系数之和[30]:
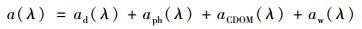
|
(3) |
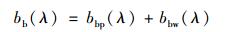
|
(4) |
式中, ad、aph、aCDOM、aw分别代表非色素颗粒物、色素颗粒物、黄色物质和纯水的吸收系数. bbp和bbw分别代表非色素颗粒物和纯水后向散射系数.其中纯水的吸收和后向散射取值参照Pope等[31]的研究结果.非色素颗粒物、色素颗粒物的吸收系数通过下式计算:
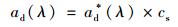
|
(5) |
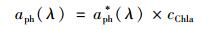
|
(6) |
式中, ad*为非色素颗粒物的比吸收系数, cs为总悬浮物浓度(mg·L-1), aph*为色素颗粒物的比吸收系数, cChla为叶绿素a浓度(μg·L-1).
黄色物质吸收系数可以利用指数函数进行参数化:
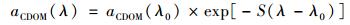
|
(7) |
式中, aCDOM(λ0)为参考波段λ0处的黄色物质吸收系数, λ0通常取440 nm. S为黄色物质的斜率指数.
非色素颗粒物的后向散射系数可以通过下式进行计算:
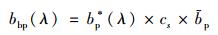
|
(8) |
式中, bp*为非色素颗粒物的比散射系数; 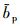
将式(5)~(7)代入式(3), 式(8)代入式(4), 进而将式(3)、式(4)代入式(2), 得到式(9):

|
(9) |
式(1)和(9)表明, 遥感反射率Rrs可以表示为cs、cChla和aCDOM(440)的函数.
1.3.2 光谱库的生成将水体不同的3组分浓度[cs、cChla、aCDOM(440)]组合代入式(9), 再代入式(1), 即可得到不同水色要素组成下的水体遥感反射率.本研究中, 将3组分浓度cs、cChla和aCDOM(440)的变化范围分别设定为:0~3 000 mg·L-1、0~300 μg·L-1和0~2 m-1; 步长分别设定为50 mg·L-1、10 μg·L-1和0.2 m-1; 共计生成20 801条高光谱数据, 将此数据作为高光谱数据库.为了提高计算效率, 参照常用高光谱数据波段设置以及水色要素反演波段常用宽度, 设定400~900 nm波段范围内, 5 nm波长间隔的101个波段数据为1条高光谱数据.
利用5种多光谱传感器(包括MERIS、MODIS Aqua、ⅦRS、GOCI、Sentinel-2A MSI)官方发布的波段响应函数, 将高光谱库数据重采样为多光谱数据.光谱重采样方法的详细步骤参照文献[25].
1.3.3 基于K-SVD算法的字典学习采用字典学习领域常用的K-SVD算法[15]对高光谱数据库和多光谱数据库进行字典学习, 生成包含200个原子的冗余字典.其中, 高光谱冗余字典Dh为101×200的矩阵(101为高光谱数据在400~900 nm范围内的波段数), 多光谱冗余字典Dm为n×200的矩阵(n为多光谱数据波段数量).
1.3.4 水体遥感反射率的高光谱重构对每一条水体高光谱(N个波段)数据Rh, Dh为N维空间中的K组基向量, 也被称为字典.当K≥N时, 目标光谱Rh可以用下式进行表达:
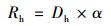
|
(10) |
式中, α代表稀疏系数, Dh代表高光谱冗余字典.
在压缩感知重构中, 常用的稀疏字典有DCT基、小波基、Gabor基等形式, 这些特定数学模型构建得到的字典具有较好的普适性, 但难以针对信号的稀疏特征进行自适应调整[33].近年来在图像处理领域多采用自适应字典训练方法, 采用样本训练的手段构建的字典, 在对目标信号进行表达时稀疏性更强[18].本研究中, 训练样本来自样本变化范围极大的模拟数据集, 字典一旦建立, 理论上具有一定的普适性.
由于K≥N, α的求解是一个欠定问题.因此对于一条多光谱数据, 可以利用α的稀疏性进行约束, 通过下式进行求解:
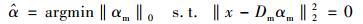
|
(11) |
式中, Dm代表多光谱冗余字典, αm代表多光谱稀疏系数.对每条多光谱数据, 稀疏系数
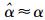


|
(12) |
高光谱数据波段间具有很高的相关性, 有学者直接利用波段间的相关性进行高光谱重构研究.参照文献[12]的方法, 建立多元线性回归模型, 对多光谱数据进行高光谱重构, 其表达式如下:
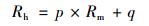
|
(13) |
式中, p和q代表线性回归拟合系数矩阵, Rh代表高光谱反射率数据矩阵, Rm代表多光谱反射率数据矩阵.
1.5 精度评价本研究利用平均相对误差(MAPE)和均方根误差(RMSE)来评价光谱重构算法及反演模型误差的精度.平均相对误差和均方根误差的计算公式可以参考文献[25].
2 结果与讨论 2.1 水色光谱及水色要素特征分析太湖和杭州湾水质参数浓度统计信息如表 1所示.由于杭州湾水域悬浮泥沙含量占主导, 叶绿素浓度较低, 所以本次实验未测量其叶绿素浓度.从表 1中可以看出, 2013年5月太湖叶绿素a浓度和总悬浮物浓度相比于2013年8月采样数据, 其浓度整体偏低; 杭州湾总悬浮物浓度要显著高于太湖总悬浮物浓度.
|
|
表 1 水色要素信息统计 Table 1 Statistics for the water color information |
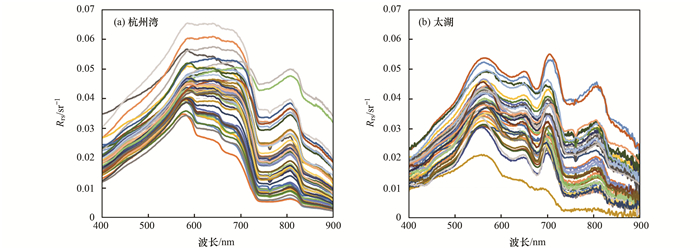
太湖与杭州湾实验获取的水面以上高光谱遥感反射率曲线如图 3所示, 其中图 3(a)是杭州湾遥感反射率曲线, 图 3(b)是太湖遥感反射率曲线.由于水体组分组成的差异, 两个研究区的光谱反射率曲线差异明显.由于杭州湾水体3组分中以悬浮颗粒物为主, 有强烈的后向散射, 所以杭州湾地区水体反射率整体偏高.同时, 由于水体叶绿素a浓度很低, 所以在680 nm左右没有明显的反射谷(主要由色素颗粒物的吸收峰造成), 在700 nm左右也没有反射峰信息(主要由叶绿素荧光作用产生).太湖地区反射率曲线整体偏低, 680 nm的反射谷和700 nm的反射峰清晰可见.
|
图 3 杭州湾和太湖水体遥感反射率曲线 Fig. 3 Above-water remote sensing reflectance collected at Hangzhou Bay and Lake Taihu |
综上所述, 在两个研究区采集得到的水色要素和光谱数据存在明显差异, 光谱重构难度较大.
2.2 光谱重构结果分析为验证光谱重构算法精度, 首先将地面实测99条高光谱遥感反射率, 利用光谱响应函数, 重采样到对应多光谱传感器(Sentinel-2A MSI、MERIS、MODIS Aqua、GOCI以及ⅦRS)的波段, 获得相应的多光谱数据.然后, 结合对应多光谱冗余字典进行稀疏分解, 获得稀疏系数.最后, 将稀疏系数应用于高光谱冗余字典, 完成高光谱重构.对多元回归重构算法, 利用生物光学模型模拟获得的数据集, 结合公式(13)获得针对每个传感器的多元回归重构拟合系数.最后, 将多元回归重构拟合系数应用于多光谱数据完成高光谱重构.最终, 将重构结果与实测高光谱数据进行对比, 分析光谱重构精度.
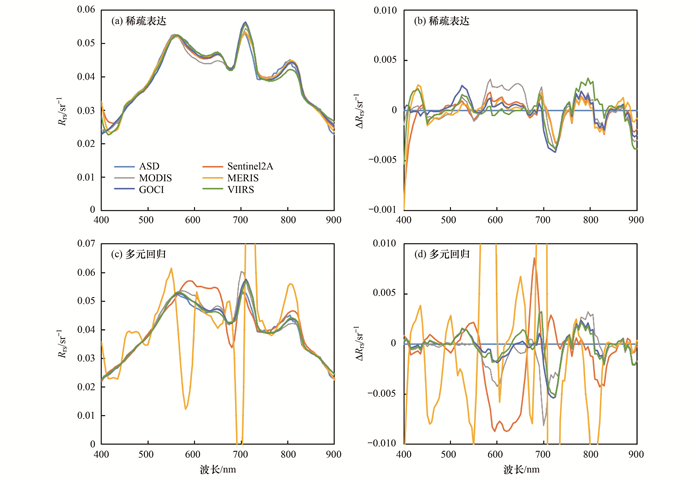
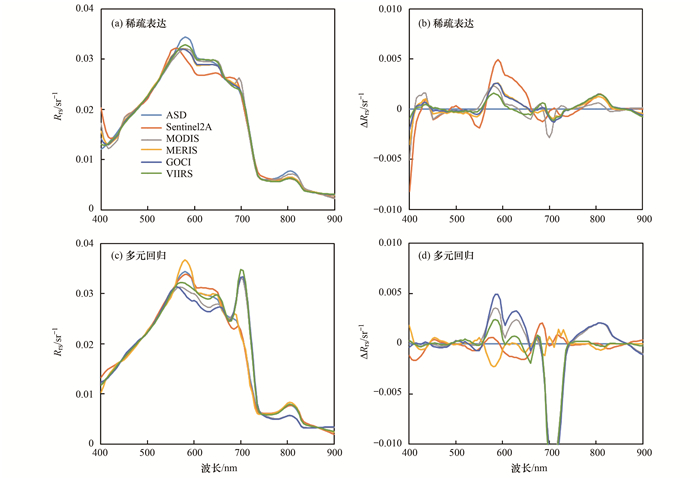
在此, 本研究展示2条典型光谱经2种重构方法在5种传感器上得到的重构高光谱及其与实测高光谱之间的偏差ΔRrs(ASD实测数据与重构数据间差值)分析结果.第一条光谱曲线采集于太湖, 其对应点位的叶绿素a浓度为108.112 μg·L-1, 总悬浮浓度为139.500 mg·L-1.从光谱曲线形态特征来看, 光谱曲线体现了丰富的色素颗粒物吸收、散射特性, 680 nm处的波谷和710 nm处的波峰都比较明显(图 4).第二条光谱曲线采集于杭州湾, 该点对应的总悬浮物浓度为37.229 mg·L-1.从光谱曲线形态特征来看, 680 nm和710 nm附近的谷峰特征信息模糊(图 5).
|
图 4 太湖典型光谱重构结果及其精度分析 Fig. 4 Comparison between two hyperspectral reconstruction methods with typical spectra collected at Lake Taihu |
|
图 5 杭州湾典型光谱重构结果及其精度分析 Fig. 5 Comparison between two hyperspectral reconstruction methods with typical spectra collected at Hangzhou Bay |
从图 4和图 5中可以看出, 基于稀疏表达重构方法获得的光谱重构结果在不同传感器之间差别很小且精度较高.说明基于模拟数据集构建的冗余字典包含了大部分实测光谱信息, 使得在目前构建的冗余字典维度下, 可以获得较好的重构精度.其次, 多元回归算法在小于550 nm以及大于750 nm的波段范围内可以得到较好的效果, 但在550~750 nm之间重构效果不太理想.同时, 多元回归重构方法得到的光谱曲线在不同传感器之间差别较大.例如, 对于MERIS传感器, 太湖典型光谱的重构结果在580 nm附近出现了明显的低估[图 4(c)], 杭州湾典型光谱的重构结果在710 nm处出现了异常的叶绿素荧光峰[图 5(c)].然而, 多元回归重构方法在Sentinel-2A MSI传感器上精度较高.整体上看, 5种常见水色多光谱传感器在应用基于稀疏表达的光谱重构算法后, 能较准确地还原ASD实测光谱曲线的特征峰谷信息.然而, 基于多元回归重构方法得到的重构光谱在不同传感器间和不同波段范围内精度差异明显.
最后, 逐波段的统计不同方法获得的重构光谱与ASD实测光谱间的误差信息, 结果如图 6所示.从结果中可以看出, 在多数传感器中(Sentinel-2A除外), 多元回归重构方法在580 nm、700 nm和710 nm附近的波段范围内存在较大误差, 特别在710 nm附近, MAPE达到40%以上.然而, 稀疏表达重构方法在400~900 nm波段范围内, 对5种传感器MAPE均值均在10%以内, RMSE均值均在0.005 sr-1以内.说明相比于多元回归方法, 稀疏表达方法在全波段上具有明显优势.
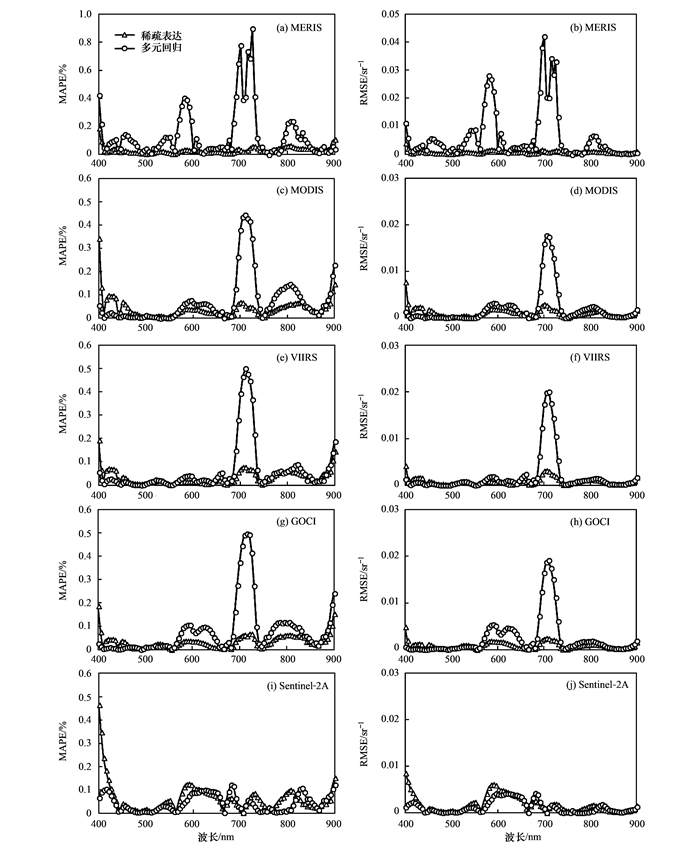
|
图 6 重构高光谱数据与实测高光谱数据的误差统计 Fig. 6 Error statistics for reconstructed hyperspectral data and in situ spectra |
为进一步验证重构算法在水色要素估算方面的适用性, 本研究利用重构光谱与实测水质参数进行相关性统计分析, 遴选最优估算光谱因子, 并将最优估算光谱因子应用于GOCI影像, 进行水质参数遥感估算.具体包括以下3个部分:首先, 利用地面实测光谱数据分别和叶绿素a浓度、总悬浮物浓度构建相应的遥感反演模型, 确定最优反演光谱因子; 其次, 分别利用基于稀疏表达和多元回归方法获得的重构高光谱, 与两种水质参数构建相应的遥感反演模型, 对比两种光谱重构方法在水质参数估算方面的精度差异; 最后, 利用基于稀疏表达方法获得的重构高光谱, 结合第二步获得的最优反演模型和同步GOCI影像, 进行叶绿素a浓度和总悬浮浓度反演, 验证反演精度, 获取两种水质参数时空分布.
在水质参数反演模型构建方面, 基于太湖和杭州湾的实测数据, 参考已发表的相关算法, 运用相关性分析和回归分析方法, 经反复比对, 以最小MAPE和RMSE为遴选标准, 最终确定最优估算因子及反演模型.对叶绿素a浓度反演模型而言, 本研究对比了目前较成熟的波段比值算法[8]和三波段[7]算法; 悬浮物浓度反演对比了单波段[34]和波段比值[35]算法.为方便对比, 将原位实测高光谱遥感反射率, 重采样到5 nm的光谱分辨率, 作为参考数据源进行反演模型构建和精度对比.在模型构建及验证中, 利用2013年8月太湖数据和2017年7月杭州湾数据(30个)分别进行太湖叶绿素a浓度和总悬浮物浓度及杭州湾总悬浮物浓度估算模型的构建.利用2013年5月13日太湖数据、2017年7月23日杭州湾数据(20个)及同步过境的GOCI影像对反演模型进行精度验证.以原位高光谱遥感反射率、基于稀疏表达重构高光谱遥感反射率和基于多元回归方法的重构高光谱遥感反射率分别构建的叶绿素a浓度和总悬浮物浓度最优反演模型和精度对比结果如表 2和表 3所示.
|
|
表 2 基于不同数据源的叶绿素a浓度反演模型构建及精度对比 Table 2 Development of the cchla retrieval model and comparison based on different data sources |
|
|
表 3 基于不同数据源的总悬浮物浓度反演模型构建及精度对比 Table 3 Development of the cs retrieval model and comparison based on different data sources |
从估算结果与实测结果的相关性来看, 由于ASD高光谱数据具有更多特征光谱信息, 因此模型决定系数(R2)最高.多光谱数据由于波段设置的限制, 特征光谱信息受到模糊, 所以模型R2有不同程度的降低.在叶绿素a浓度估算模型中, 原始多光谱Sentinel-2A MSI数据效果最好, R2达到0.731, 在总悬浮物浓度估算模型中, MODIS Aqua数据效果最好, R2达到0.803.从基于重构光谱所得模型的拟合情况来看:①利用稀疏表达算法重构所得光谱数据所构建的模型具有较好的模型解释能力, R2都在0.8左右; ②利用多元线性回归方法重构所得光谱数据构建的模型在不同传感器之间解释力差异明显, R2波动较大且显著低于由实测高光谱所构建的模型R2.例如, 基于Sentinel-2A MSI数据的多元线性回归重构光谱因子与叶绿素a浓度之间的R2能达到0.714, 而对MERIS数据而言, R2只有0.011.类似地, 多元线性回归重构光谱因子与总悬浮物浓度在MERIS传感器上R2只有0.357, 显著低于ASD光谱数据的R2(0.805).因此, 上述结果表明:①稀疏表达重构方法在得到丰富光谱信息的同时, 能够保证光谱信息的准确性, 适用于水色要素的估算研究; ②多元线性回归重构方法, 在不同传感器之间精度差异明显, 存在损失有用信息的情况, 会影响数据源对水色要素的估算能力.
最后, 结合2013年5月13日以及2017年7月23日的GOCI影像, 进行算法的适用性验证.利用稀疏表达重构方法, 对经过大气校正的GOCI影像进行光谱重构, 得到重构高光谱影像数据.然后, 结合最优反演模型, 进行水体叶绿素a浓度和总悬浮颗粒物浓度估算.通过与实测数据对比(图 7)可以看出, 经光谱重构后的数据, 对叶绿素a浓度和总悬浮浓度估算精度均有所提升.其中, 在叶绿素a浓度估算结果上差异比较明显, 利用重构数据估算所得结果更接近1:1线.统计结果显示, 重构数据与GOCI数据估算结果的RMSE分别为7.125 μg·L-1和12.175 μg·L-1, MAPE分别为51.5%和80.6%, 可见重构数据对叶绿素a浓度的估算精度有明显改善.虽然重构GOCI数据与原始GOCI数据对总悬浮物浓度估算结果差异较小, 但精度也有提升.统计结果显示, 重构数据与GOCI数据对总悬浮物浓度估算的RMSE分别为28.596 mg·L-1和29.048 mg·L-1, MAPE分别为18.8%和19.1%.此外, 重构数据在遥感估算过程中没有产生异常数据, 表明算法稳定性较强.
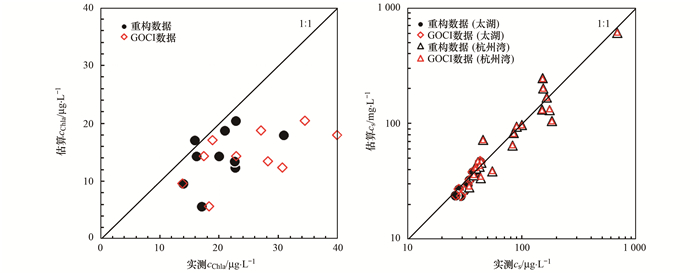
|
图 7 叶绿素a和总悬浮浓度反演估算验证散点图 Fig. 7 Scatter plot of the measured and predicted cchla and cs |
从GOCI影像估算结果来看(图 8), 2013年5月13日太湖北部的梅梁湾、竺山湾和贡湖湾这3个湖区, 以及西南沿岸湖区叶绿素a浓度较高; 总悬浮物体现出类似的特点, 湖心区浓度较低, 沿岸湖区浓度较高. 2017年7月23日杭州湾南部沿岸地区, 由于受滩涂影响, 导致总悬浮物含量较高.同时, 杭州湾跨海大桥东、西两侧总悬浮物浓度差异显著.在靠近长江口附近区域, 总悬浮物浓度有明显提升.

|
图 8 太湖、杭州湾叶绿素a和总悬浮物浓度空间分布 Fig. 8 Spatial distribution of cchla and cs at Lake Taihu and Hangzhou Bay |
(1) 本研究提出的基于稀疏表达方法的高光谱重构算法, 可以在不使用实测数据集的条件下, 实现高光谱重构.从重构光谱曲线的光谱形态及逐波段误差统计来看, 基于稀疏表达的高光谱重构算法能准确地还原光谱曲线的峰谷信息, 效果优于多元线性回归方法, 表明该算法具有较高的重构精度.
(2) 多元回归算法在不同传感器之间精度差异明显, 导致估算结果不稳定.基于稀疏表达的高光谱重构算法, 可以较好地应用于多种传感器, 精度与ASD实测数据接近.表明本研究提出的算法适用于目前大多数水色遥感传感器, 具有很强的应用潜力.
(3) 结合同步GOCI数据, 利用基于稀疏表达的高光谱重构算法对叶绿素a浓度和总悬浮浓度进行估算, 估算精度相比于原始GOCI多光谱数据有不同程度的提升, 说明基于稀疏表达的高光谱重构算法可以为水环境遥感提供更好的数据源.
| [1] |
汪嘉杨, 郭倩, 余静, 等. 城市景观水体富营养化评价的升半Г型分布指数公式[J]. 环境科学学报, 2017, 37(3): 1162-1168. Wang J Y, Guo Q, Yu J, et al. Eutrophication evaluation for urban landscape waters based on semi-Г type distribution function[J]. Acta Scientiae Circumstantiae, 2017, 37(3): 1162-1168. |
| [2] | Shi K, Zhang Y L, Xu H, et al. Long-term satellite observations of microcystin concentrations in Lake Taihu during cyanobacterial bloom periods[J]. Environmental Science & Technology, 2015, 49(11): 6448-6456. |
| [3] |
尹球, 巩彩兰, 匡定波, 等. 湖泊水质卫星遥感方法及其应用[J]. 红外与毫米波学报, 2005, 24(3): 198-202. Yin Q, Gong C L, Kuang D B, et al. Method of satellite remote sensing of lake water quality and its applications[J]. Journal of Infrared and Millimeter Waves, 2005, 24(3): 198-202. DOI:10.3321/j.issn:1001-9014.2005.03.009 |
| [4] | Palmer S C J, Kutser T, Hunter P D. Remote sensing of inland waters:challenges, progress and future directions[J]. Remote Sensing of Environment, 2015, 157: 1-8. DOI:10.1016/j.rse.2014.09.021 |
| [5] | McClain C R. A decade of satellite ocean color observations[J]. Annual Review of Marine Science, 2009, 1: 19-42. DOI:10.1146/annurev.marine.010908.163650 |
| [6] | Le C F, Li Y M, Zha Y, et al. A four-band semi-analytical model for estimating chlorophyll a in highly turbid lakes:the case of Taihu Lake, China[J]. Remote Sensing of Environment, 2009, 113(6): 1175-1182. DOI:10.1016/j.rse.2009.02.005 |
| [7] | Gitelson A A, Dall'Olmo G, Moses W, et al. A simple semi-analytical model for remote estimation of chlorophyll-a in turbid waters:validation[J]. Remote Sensing of Environment, 2008, 112(9): 3582-3593. DOI:10.1016/j.rse.2008.04.015 |
| [8] | Huang C C, Zou J, Li Y M, et al. Assessment of NIR-red algorithms for observation of chlorophyll-a in highly turbid inland waters in China[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2014, 93: 29-39. DOI:10.1016/j.isprsjprs.2014.03.012 |
| [9] | Zheng Z B, Li Y M, Guo Y L, et al. Landsat-based long-term monitoring of total suspended matter concentration pattern change in the wet season for Dongting Lake, China[J]. Remote Sensing, 2015, 7(10): 13975-13999. DOI:10.3390/rs71013975 |
| [10] | Sun D Y, Qiu Z F, Hu C M, et al. A hybrid method to estimate suspended particle sizes from satellite measurements over Bohai Sea and Yellow Sea[J]. Journal of Geophysical Research:Oceans, 2016, 121(9): 6742-6761. DOI:10.1002/2016JC011949 |
| [11] |
宋挺, 周文鳞, 刘军志, 等. 利用高光谱反演模型评估太湖水体叶绿素a浓度分布[J]. 环境科学学报, 2017, 37(3): 888-899. Song T, Zhou W L, Liu J Z, et al. Evaluation on distribution of chlorophyll-a content in surface water of Taihu Lake by hyperspectral inversion models[J]. Acta Scientiae Circumstantiae, 2017, 37(3): 888-899. |
| [12] | Sun D Y, Hu C M, Qiu Z F, et al. Reconstruction of hyperspectral reflectance for optically complex turbid inland lakes:test of a new scheme and implications for inversion algorithms[J]. Optics Express, 2015, 23(11): A718-A740. DOI:10.1364/OE.23.00A718 |
| [13] | Lee Z, Shang S L, Hu C M, et al. Spectral interdependence of remote-sensing reflectance and its implications on the design of ocean color satellite sensors[J]. Applied Optics, 2014, 53(15): 3301-3310. DOI:10.1364/AO.53.003301 |
| [14] |
郭宇龙, 李云梅, 朱利, 等. 基于HJ1A-CCD数据的高光谱影像重构研究[J]. 环境科学, 2013, 34(1): 69-76. Guo Y L, Li Y M, Zhu L, et al. Research of hyperspectral reconstruction based on HJ1A-CCD data[J]. Environmental Science, 2013, 34(1): 69-76. |
| [15] | Aharon M, Elad M, Bruckstein A. rmK-SVD:an algorithm for designing overcomplete dictionaries for sparse representation[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4311-4322. DOI:10.1109/TSP.2006.881199 |
| [16] | Wright J, Yang A Y, Ganesh A, et al. Robust face recognition via sparse representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(2): 210-227. DOI:10.1109/TPAMI.2008.79 |
| [17] | Yang J C, Wright J, Huang T S, et al. Image super-resolution via sparse representation[J]. IEEE Transactions on Image Processing, 2010, 19(11): 2861-2873. DOI:10.1109/TIP.2010.2050625 |
| [18] | Arad B, Ben-Shahar O. Sparse recovery of hyperspectral signal from natural RGB images[A]. In: Leibe B, Matas J, Sebe N, et al. European Conference on Computer Vision[M]. Cham, Switzerland: Springer, 2016. 19-34. |
| [19] | Li S T, Yang B. A new pan-sharpening method using a compressed sensing technique[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(2): 738-746. DOI:10.1109/TGRS.2010.2067219 |
| [20] | Huang B, Song H H. Spatiotemporal reflectance fusion via sparse representation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(10): 3707-3716. DOI:10.1109/TGRS.2012.2186638 |
| [21] | Elad M, Michal A. Image denoising via sparse and redundant representations over learned dictionaries[J]. IEEE Transactions on Image Processing, 2006, 15(12): 3736-3745. DOI:10.1109/TIP.2006.881969 |
| [22] | Chen Y, Nasrabadi N M, Tran T D. Hyperspectral image classification using dictionary-based sparse representation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(10): 3973-3985. DOI:10.1109/TGRS.2011.2129595 |
| [23] | Xu M, Jia X P, Pickering M, et al. Cloud removal based on sparse representation via multitemporal dictionary learning[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(5): 2998-3006. DOI:10.1109/TGRS.2015.2509860 |
| [24] | Shen F, Verhoef W, Zhou Y X, et al. Satellite estimates of wide-range suspended sediment concentrations in Changjiang (Yangtze) estuary using MERIS data[J]. Estuaries and Coasts, 2010, 33(6): 1420-1429. DOI:10.1007/s12237-010-9313-2 |
| [25] | Li Y, Zhang Y L, Shi K, et al. Monitoring spatiotemporal variations in nutrients in a large drinking water reservoir and their relationships with hydrological and meteorological conditions based on Landsat 8 imagery[J]. Science of the Total Environment, 2017, 599-600: 1705-1717. DOI:10.1016/j.scitotenv.2017.05.075 |
| [26] |
唐军武, 田国良, 汪小勇, 等. 水体光谱测量与分析Ⅰ:水面以上测量法[J]. 遥感学报, 2004, 8(1): 37-44. Tang J W, Tian G L, Wang X Y, et al. The methods of water spectra measurement and analysis Ⅰ:above-water method[J]. Journal of Remote Sensing, 2004, 8(1): 37-44. |
| [27] |
杜成功, 李云梅, 王桥, 等. 面向GOCI数据的太湖总磷浓度反演及其日内变化研究[J]. 环境科学, 2016, 37(3): 862-872. Du C G, Li Y M, Wang Q, et al. Inversion model and daily variation of total phosphorus concentrations in Taihu Lake based on GOCI data[J]. Environmental Science, 2016, 37(3): 862-872. |
| [28] | Lee Z, Carder K L, Mobley C D, et al. Hyperspectral remote sensing for shallow waters:2. Deriving bottom depths and water properties by optimization[J]. Applied Optics, 1999, 38(18): 3831-3843. DOI:10.1364/AO.38.003831 |
| [29] | Lee Z, Carder K L, Arnone R A. Deriving inherent optical properties from water color:a multiband quasi-analytical algorithm for optically deep waters[J]. Applied Optics, 2002, 41(27): 5755-5772. DOI:10.1364/AO.41.005755 |
| [30] |
刘忠华, 李云梅, 吕恒, 等. 基于生物光学模型的巢湖后向散射概率估算[J]. 环境科学, 2011, 32(2): 464-471. Liu Z H, Li Y M, Lü H, et al. Estimating of backscattering rate in Lake Chaohu based on bio-optical model[J]. Environmental Science, 2011, 32(2): 464-471. |
| [31] | Pope R M, Fry E S. Absorption spectrum (380-700 nm) of pure water. Ⅱ. Integrating cavity measurements[J]. Applied Optics, 1997, 36(33): 8710-8723. DOI:10.1364/AO.36.008710 |
| [32] |
李云梅, 黄家柱, 韦玉春, 等. 用分析模型方法反演水体叶绿素的浓度[J]. 遥感学报, 2006, 10(2): 169-175. Li Y M, Huang J Z, Wei Y C, et al. Inversing chlorophyll concentration of Taihu Lake by analytic model[J]. Journal of Remote Sensing, 2006, 10(2): 169-175. |
| [33] |
汪琪, 马灵玲, 唐伶俐, 等. 基于光谱稀疏模型的高光谱压缩感知重构[J]. 红外与毫米波学报, 2016, 35(6): 723-730. Wang Q, Ma L L, Tang L L, et al. Hyperspectral compressive sensing reconstruction based on spectral sparse model[J]. Journal of Infrared and Millimeter Waves, 2016, 35(6): 723-730. |
| [34] | Shi K, Zhang Y L, Zhu G W, et al. Long-term remote monitoring of total suspended matter concentration in Lake Taihu using 250 m MODIS-Aqua data[J]. Remote Sensing of Environment, 2015, 164: 43-56. DOI:10.1016/j.rse.2015.02.029 |
| [35] | He X Q, Bai Y, Pan D L, et al. Using geostationary satellite ocean color data to map the diurnal dynamics of suspended particulate matter in coastal waters[J]. Remote Sensing of Environment, 2013, 133: 225-239. DOI:10.1016/j.rse.2013.01.023 |
 2019, Vol. 40
2019, Vol. 40


