土壤作为一种不可再生的自然资源, 是人类生存和发展的物质基础.然而, 随着人类社会的发展, 工业“三废”排放、生活垃圾积累、农药化肥过度使用等造成了严重的土壤污染问题[1, 2].其中, 由于土壤重金属污染物具有难降解、隐蔽性高、易被富集和可以通过食物链进入人体等特点, 成为影响我国土壤环境质量的重要因素之一[3, 4].
为了解区域土壤重金属污染的空间分布特征、污染程度和污染风险, 我国在全国范围内开展了土壤污染调查和治理工作, 并在局部重金属高背景区域进行高密度采样分析[5, 6].但即使是在高密度采样的条件下, 土壤样点数量还是有限的, 需要借助地统计学的空间插值方法来建立重金属元素含量的连续性表面[7, 8].因此, 空间插值方法的优选是准确预测区域土壤重金属元素含量空间分布特征和污染风险的关键.
针对此问题, 学者对反映元素含量空间分布特征的反距离权重法(inverse distance weighted, IDW)、径向基函数法(radial basis function, RBF)、局部多项式法(local polynomial interpolation, LPI)和普通克里格法(ordinary kriging, OK)这4种空间插值方法进行了大量的研究.例如, 李凯等[9]以某镇土壤中Cd为例, 将2 033个样点随机抽取为1 830、1 423、1 017、610、203这5个子样进行研究发现:在2 033个样点数量下, IDW法的插值效果最优, 考虑到采样的成本, 1 017个左右样点是该镇域内较合理的采样数量; 陈思萱等[10]对广东某地区土壤中具有较强变异性的As插值表明: IDW法插值效果最佳, OK法平滑效应较明显.张金兰等[11]对广东某地区土壤中具有中等空间自相关性的Cd插值表明: RBF法和IDW法插值效果优于OK法, OK法表现出较强的平滑效应, 而RBF法插值精度最高.李湘凌等[12]对合肥义城地区土壤重金属插值表明:以元素空间分布而言, OK法对Cu、Pb、As最优, IDW法对Zn最优, RBF法对Cd、Hg最优, 但OK法相比于IWD法和RBF法操作较为复杂.可以看出, 由于不同研究区采样点的密度、元素空间相关性、插值参数选择和结果分析方法等不同, 使得最优插值方法的选取具有不确定性.
以上4种空间插值方法主要是对区域内重金属元素含量的空间分布特征进行预测, 但有时人们关心的是重金属元素含量污染概率分布特征.指示克里格法(indicator kriging, IK)能给出单一变量超过或低于某规定阈值的风险概率, 因而对重金属元素污染评价具有较好的应用前景[13~15].例如, 杨奇勇等[13]采用GB 15618-1995《土壤环境质量标准》中的二级标准值, 利用IK法对土壤重金属的污染进行评估, 结果表明:研究区存在As、Cd、Cu等重金属污染.但前人的研究中, 以地累积指数(index of geoaccumulation, Igeo)所对应的重金属元素含量作为评价阈值, 反映元素在不同污染等级的污染概率研究还较少.
本文以研究区表层土壤重金属As和Cd为例, 在数据分析转化和选择最优插值参数的前提下, 运用IWD、RBF、LPI和OK法这4种方法进行空间插值, 对插值结果进行交叉验证分析和评价, 对比选择了最优空间插值方法.利用IK法对研究区As和Cd的污染进行评估, 以期为其它土壤重金属高背景区高密度采样下的土地质量地球化学调查和污染评价提供技术参考.
1 材料与方法 1.1 研究区概况研究区位于湖北省恩施市东北边陲, 面积约50 km2.该区域属亚热带季风性湿润气候, 全年降水量1 100~1 400 mm, 年平均日照1 350~1 860 h, 相对湿度70%~80%, 年平均气温15℃.研究区地形为山地, 地势起伏大, 海拔在273~1 428 m之间(图 1).区内主要土壤类型为黄棕壤和黄壤, 主要土地利用类型有旱地、水田和林地.该区经济发展以农业为主, 区内种植玉米、水稻、烟叶、魔芋、蔬菜等多种作物.
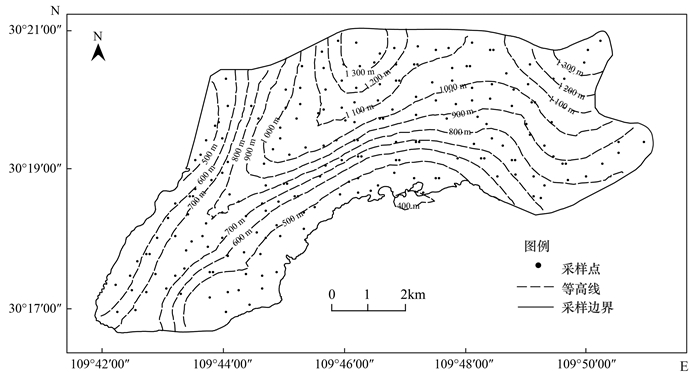
|
图 1 研究区采样点位示意及等高线 Fig. 1 Sampling sites and contour lines in the study area |
样品的采集、加工和测试分析严格按照《DZ/T 0295-2016土地质量地球化学评价规范》的要求进行[16].在研究区内采用网格化布点和土地利用图斑布点相结合, 每0.25 km2一个采样点.在布设的采样点上, 以GPS定位点为中心, 采用梅花形布点法采集3~5个子样, 每个子样均使用竹铲, 垂直采集0~20 cm的土柱, 并去除杂草、砾石、肥料块等杂质, 等份组合成一个混合样, 共获取土壤样品199件(图 1).采集的土样, 悬挂在室内自然阴干, 阴干后用木锤碾细, 过孔径为2 mm的尼龙筛, 未过筛的土粒重新碾压, 直至全部样品通过.过筛后的土样混合均匀, 装尼龙自封袋送至实验室进一步加工、测试.
室内将样品进一步用球磨机碾碎过200目筛, 土壤重金属全量采用HNO3-HCl-HF-HClO4溶样, As含量的测定采用原子荧光光度法(ICP-MS, X-SERIES Ⅱ, Thermo Electron, 美国), 检出限为0.2mg·kg-1; Cd含量的测定采用原子吸收分光光度法(AAS, novAA 350, Analytik Jena, 德国), 检出限为0.02 mg·kg-1.分析过程利用国家标准土样(GSS-17、GSS-22、GSS-25、GSS-27)监控测试分析的准确度, 采用密码样监控测试分析的精密度, As和Cd含量分析的准确度和精密度均在监控限内, 测试结果可靠.
1.3 空间插值与精度评价方法 1.3.1 反距离权重法反距离权重法(IDW)基于相近相似的原理, 即在同一个区域内, 两个测量点距离越近, 则测定参数越相似, 反之, 距离越远则相似性越小.它以插值点与样本点间的距离为权重进行加权平均, 离插值点越近的样本点赋予的权重越大[17].其公式为:
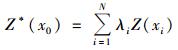
|
(1) |
式中, Z*(x0)为x0点处的预测值; N为用于插值的周围样点的个数; Z(xi)为样点xi处的实测值; λi为第i个样点对预测点的权重, 它由式(2)计算:
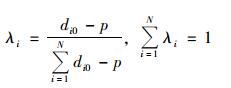
|
(2) |
式中, di0为预测点x0与各样点间的距离; p为距离的幂, 即随样点与预测点距离的增加, 样点对预测点权重的影响按指数规律减少; 权重值的总和为1.
1.3.2 径向基函数法径向基函数法(RBF)如同将一个软膜插入并经过各已知样点, 同时要求表面的总曲率最小.包括5种不同的基础函数:平面样条函数(thin-plate spline)、张力样条函数(spline with tension)、规则样条函数(completely regularized spline)、高次曲面函数(multiquadric functions)和反高次曲面样条函数(inverse multiquadric spline).径向基函数法适用于对大量样点的数据进行插值计算, 同时要求获得平滑表面的情况[17].
1.3.3 局部多项式法局部多项式法(LPI)应用最小二乘法来拟合数据, 通常选择一次、二次和三次多项式, 通过采用多个多项式作为局部方程式来拟合整个研究区域, 每个多项式都处于特定重叠的邻近区域内.根据已知样点拟合的多项式和预测点的坐标, 计算预测点的值.局部多项式法适用于确定变量的小范围变异和得到一个平滑的表面[17, 18].
1.3.4 普通克里格法克里格法(Kriging)以变异函数理论模型和结构分析为基础, 在局部区域内对区域变量进行无偏最优估计, 是地统计学的主要插值方法之一.普通克里格法(OK)是克里格法中最常用的一种方法, 前提要求数据成正态或近似正态分布.在满足固有假设条件下, OK法的估计公式与IDW法的公式相同, 不同的是OK法权系数λi的确定不仅与距离有关, 还通过使用半变异函数, 考虑了已知样点和预测点的空间方位关系.当区域化变量满足二阶平稳性和本征假设时, 半变异函数可用式(3)计算:

|
(3) |
式中, γ(h)为半变异函数; h为滞后距离或步长; N(h)为距离等于h的样点的对数; Z(xi)和Z(xi+h)分别为区域化变量Z(x)在位置xi和xi+h处的实测值.
半变异函数常用的拟合模型有:线性模型(Linear)、球类模型(Spherical)、指数模型(Exponential)和高斯模型(Gaussian), 所拟合的变异函数模型反映了区域化变量的结构性和随机性.在使用OK法进行空间插值过程中, 选择最优的拟合模型有利于提高插值的精度[19].
1.3.5 交叉验证法交叉验证法(cross validation)通过分别假设每一个样点的未知值, 利用周围样点和所用的插值方法来预测该样点的值, 以样点的真实值和预测值之间的误差来评价插值方法的优劣[20].常用的评价指标有平均误差(average error, ME)和均方根误差(root mean square error, RMSE). ME越接近0说明插值越无偏; RMSE越小说明误差均值的变化范围越小[18, 21].其表达式分别为:
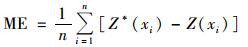
|
(4) |

|
(5) |
式中, Z*(xi)为样点xi的预测值; Z(xi)为实测值.
不精确度(imprecision, IP)是预测误差的变差, IP越小, 插值精度越高[21, 22].其公式为:
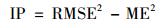
|
(6) |
地累积指数(Igeo)由德国科学家Muller于1969年提出, 最初被用于定量评价水环境沉积物中的重金属污染程度, 由于该评价方法的科学性和直观性, 近年来被学者们广泛地用于土壤重金属污染评价[23].地累积指数法不仅可以反映土壤重金属的自然分布特征, 还可以判别人为因素对土壤环境的影响[24].其表达式为:
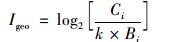
|
(7) |
式中, Igeo为地累积指数; Ci为i元素含量的实测值; Bi为i元素含量的背景值; k为修正系数, 一般取1.5.
深层土壤受到人为因素影响较小, 重金属含量特征主要受地理因素的影响[14].以湖北省深层(C层)土壤重金属含量的算术平均值作为背景值, 分析研究区表层土壤中As和Cd的污染状况(表 1).
|
|
表 1 湖北省土壤元素背景值[25] Table 1 Soil elements background values in Hubei Province |
1.4.2 指示克里格法
指示克里格(IK)属于非线性、非参数克里格插值法, 它将区域化变量转化为对其指数函数的研究, 用来估计超过预先设定的某一阈值的概率[26].与普通克里格插值方法相比, 指示克里格插值法不需要原始数据成正态分布或对异常值进行剔除, 能更加真实地反映土壤数据的空间变异特征[14].
1.5 数据分析与处理本文在研究中用SPSS 19.0(美国国际商业机器公司)和EXCEL 2007(美国微软公司)进行数据的处理和描述性统计; 用GS+7.0(美国伽马软件设计公司)对数据进行半方差函数拟合和空间结构分析; 插值参数的优化、交叉验证、空间插值和制图用ArcGIS 10.2(美国环境系统研究所公司)完成.
普通克里格法(OK)使用前提, 要求数据符合正态分布, 否则会产生比例效应, 影响预测精度[27].故采用偏度、峰度和Kolmogorov-Smirnove(K-S)对As和Cd进行正态分布检验.由表 2可知, As原始数据服从正态分布(P>0.05), 对不符合正态分布的Cd进行自然对数转换, 转换后的数据符合正态分布(P>0.05).
|
|
表 2 土壤中As和Cd的偏度和峰度 Table 2 Skewness and kurtosis values for As and Cd in soil |
2 结果与分析 2.1 研究区土壤As和Cd含量的描述性统计
研究区199个表层土壤样点中As和Cd含量的统计结果见表 3. As和Cd含量变化范围均较大, 分别介于6.3~28.4mg·kg-1和0.21~21.95mg·kg-1之间. As和Cd平均含量分别为14.6mg·kg-1和2.12mg·kg-1, 均超过湖北省土壤背景值(表 1), 分别是背景值的1.10和15.14倍, Cd积累情况较严重.变异系数的大小可以反映元素在土壤中的均匀性和变异性[28], As含量变异系数小于0.25, 呈低变异, 在研究区内分布较均匀, 受到人类活动影响较小; Cd含量变异系数高达1.43, 属强变异, 在研究区内分布不均匀, 可能受到了人类活动的影响.
|
|
表 3 土壤中As和Cd含量的描述性统计 Table 3 Descriptive statistics of concentrations of As and Cd in soil |
2.2 土壤As和Cd的插值研究 2.2.1 最优插值参数的确定与半变异函数的拟合
同一种插值方法参数选择的不同会影响插值的结果, 为尽可能减少误差, 插值方法的比较应建立在参数最优的前提下[29]. IDW法的参数较少, 易于选择最优的幂值(Power). RBF和LPI法参数较多, 需要用交叉验证的方法进行检验, 最优参数根据误差最小的原则选取, 结果见表 4.
|
|
表 4 各插值方法的最优参数 Table 4 Best parameters for each interpolation method |
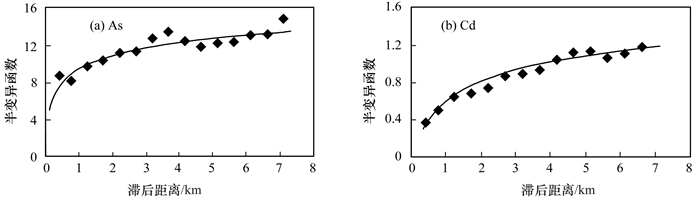
OK法参数选取较复杂, 主要体现在半方差函数拟合上, 半方差函数分析前提要求变量满足正态分布, 分析前对Cd含量进行自然对数转换, 使其符合正态分布.通过反复尝试, 半变异函数理论模型的拟合结果见图 2, As和Cd均以指数模型拟合最优, 决定系数(R2)分别为0.85和0.98(表 5).块金系数表示元素空间异质性程度, 是反映区域化变量空间相关性程度的指标.块金系数小于0.25, 表明变量空间自相关性强, 主要受结构性变异影响; 块金系数介于0.25~0.75之间, 变量空间自相关性中等; 块金系数大于0.75, 表明变量空间自相关性较弱, 主要受随机因素影响[2, 30]. As的块金系数为0.5, 介于0.25~0.75, 空间自相关性中等, 说明As受结构性因素(母质、地形、土壤类型等)和随机性因素(耕作、施肥、点源污染等)综合影响; Cd的块金系数为0.79, 大于0.75, 空间自相关性较弱, 说明Cd受随机性因素影响较强.
|
图 2 土壤中As和Cd含量的半变异函数拟合 Fig. 2 Semivariogram fitting plots of heavy metals As and Cd in soil |
|
|
表 5 土壤中As和Cd含量的变异参数 Table 5 Semivariogram parameters for concentration As and Cd in soil |
2.2.2 插值结果的交叉验证
在各插值方法选择最优参数的前提下, 交叉验证结果见表 6. As的4种插值方法中, ME最接近0的是LPI法, RMSE最小的是RBF法, IP最小的也是RBF法. IP越小插值精度越高, 对As而言, 4种插值方法的插值精度为RBF法>IDW法>OK法>LPI法. Cd的4种插值方法中, ME最接近0的是RBF法, RMSE最小的是OK法, IP最小的也是OK法.对Cd而言, 4种插值方法的插值精度为OK法>LPI法>RBF法>IDW法.
|
|
表 6 土壤中As和Cd含量的交叉验证结果/mg·kg-1 Table 6 Cross validation results of concentration of As and Cd in soil/mg·kg-1 |
2.2.3 土壤重金属As和Cd含量的空间分布特征
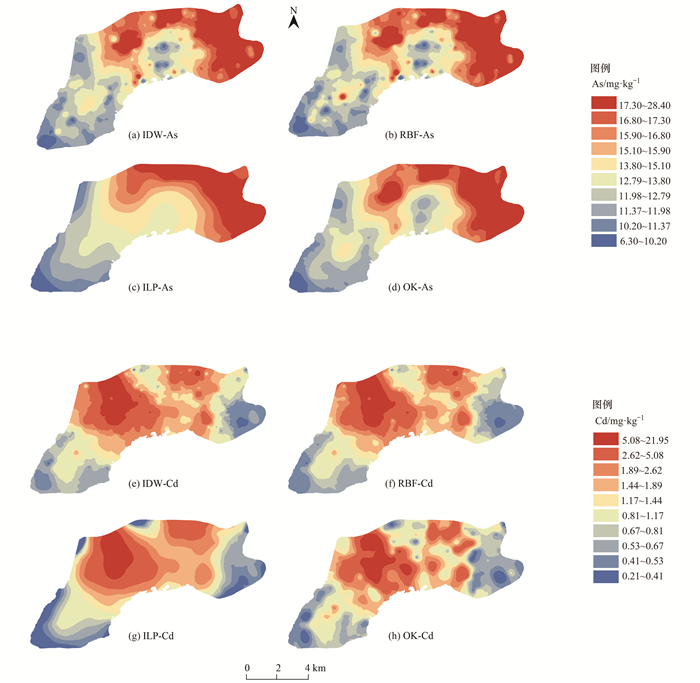
4种插值方法均在使用最优参数的前提下进行插值运算, 将重金属元素As与Cd的含量按分位数分为10个频率区间, 绘制As与Cd含量的空间分布图(图 3).可以看出, 对同一种元素而言, 不同插值方法的插值结果表现出相似的空间分布特征, 但对元素含量预测的详细程度, 相同含量区间分布的形状、面积大小均不同.
|
图 3 土壤中As和Cd含量空间插值 Fig. 3 Spatial distribution plots of concentration of As and Cd in soil |
As在研究区的西南部含量较低, 在北部和东北部的含量较高, 含量呈从西南向东北逐渐升高的趋势, 具有良好的连续性. LPI法很好地反映了As含量的这一变化趋势[图 3(c)], 但平滑效应过于明显, 不能准确地反映点源污染和小范围的面源污染, 其插值结果不如其它3种方法详尽. IDW、RBF和OK法插值结果的相似度较高, 其中RBF法反映出As在研究区西南部的一处点源污染[图 3(b)], 结果更为详尽, 对污染区的面积估计也较其它两种方法更为准确, 其次是IDW法[图 3(a)]; Cd在研究区中部含量较高, 在西南和东北含量较低, 含量变化趋势不明显. LPI法插值结果较其它3种方法较差[图 3(g)], 平滑效应明显, 对污染面积估计较大.其它3种插值方法的插值结果相近, 其中OK法对污染区面积估计相对较小[图 3(h)].
2.3 土壤中As和Cd的污染评价 2.3.1 地累积指数法污染评价以湖北省深层土壤元素含量的算术平均值作为背景值进行污染评价, 研究区土壤As和Cd的地累积指数和污染程度见表 7. As的超标样点有11个, 所占比例为5.5%, 超标样点均处于轻度-中度污染程度, 污染程度低; Cd超标样点有197个, 所占比例高达99.0%, 其中处于中度污染、中度-强污染和强污染程度的样点所占比例分别为30.2%、25.1%、18.1%.此外, 少数样点还处于强-极严重污染和极严重污染程度, 研究区Cd累积明显, 污染程度高.
|
|
表 7 土壤中As和Cd的地累积指数 Table 7 Geo-accumulation index for As and Cd in soil |
2.3.2 Cd污染程度概率空间分布特征
研究区As整体处于无污染, 故采用IK法只对重金属Cd污染概率进行分析, 结果如图 4所示. Igeo=0表示临界污染情况, 将Igeo=0时对应的Cd含量作为阈值, Cd元素临界污染概率最大值为1, 研究区几乎整个范围内都存在着Cd污染情况[图 4(a)], 污染概率较高.将阈值分别提高到Igeo=1和Igeo=2进行插值.当Igeo=1时, Cd元素中度污染概率最大值为1, 高值区主要分布在研究区的中部和北部[图 4(b)], 达到中度污染程度, 分布范围较广; 当Igeo=2时, Cd元素中度-强污染概率最大值仍达到1, 高值区主要还是分布在研究区的中部区域[图 4(c)], 分布范围相对减小, 但污染程度较高, 达中度-强污染程度.总体而言, 在采用重金属污染阈值评价污染程度情况下, 研究区表层土壤中As整体无污染, 而Cd具有较高的污染概率.

|
图 4 土壤中Cd的污染概率空间分布 Fig. 4 Spatial distribution plots of pollution probability for Cd in soil |
在各插值方法均使用最优参数和拟合模型的前提下, 从交叉验证的结果来看(表 6), 各插值方法均存在预测误差.对As而言, LPI法的IP值较其它3种方法的IP值稍大, 表现出一定的劣势; 对Cd而言, OK法的IP值稍小, 表现出一定的优势.但同一种元素各插值方法的IP值相差均小于0.1 mg·kg-1, 预测精度差异不大, 很难直接根据交叉验证的结果来判断插值方法的优劣.
从元素含量的空间分布特征进行分析(图 3). LPI法利用最小二乘法拟合元素含量的空间分布趋势, 趋向于得到一个平滑的表面[21, 31].这导致LPI法不能反映As和Cd局部点源污染的信息, 平滑作用较其它3种方法过于明显. OK法以元素的结构特征为基础, 确定真实值对预测值的影响权重, 理论上是最佳的估计方法[18, 32].但是, 半方差函数拟合具有主观性, 不同的研究者可能会有不同的结果.同时, OK法也存在着较强的平滑效应, 可能会丢失局部最大值和最小值信息, 这在As含量的空间分布特征中表现得较明显.有学者认为OK法在元素含量变异大、空间自相关性较差的区域会表现出较强的平滑效应[33].这可能是因为OK法对空间自相关性差的元素含量进行对数转换后, 压缩了数据的变化范围, 表现出较强的平滑效应. IDW法和RBF法都属于确定性插值, 即样点处的真实值与预测值相等, 插值结果极大地保留了元素含量的极大值和极小值信息[34].两种方法的区别在于IDW法根据距离确定权重, 而RBF法根据局部平滑趋势确定权重[18].这也使得As和Cd元素含量空间分布图表现出较强的“牛眼效应”, 且对污染区域面积的估计也较OK法要大.
总体而言, 在局部重金属高背景区进行高密度采样下, 为准确地了解重金属污染情况, IDW法和RBF法对局部极值的反映更加详尽, 插值效果较好.同时, RBF法和IDW法的参数较少, 更容易操作.而OK法插值前需要对数据进行统计检验、数据转换、空间结构分析和半方差函数拟合等, 操作较复杂.
4 结论(1) 基于插值结果的交叉验证精度评价, 对研究区As含量预测, RBF法和IDW法的精度略高于OK法和LPI法; 对Cd含量预测, OK法和LPI法的精度略高于RBF法和IDW法.总体来看, 对同一个元素而言, 各插值方法的预测精度差异不大.
(2) 4种插值方法对研究区As和Cd含量空间分布特征的预测结果总体趋势一致, 但对局部高值的有效识别存在差异.其中LPI法和OK法, 尤其是LPI法表现出较强的平滑效应, 丢失了局部极值信息, 不利于准确地反映区域土壤重金属污染状况. IDW法和LPI法极大地保留了极值信息, 插值效果较详尽, 且更容易操作.建议在局部重金属高背景区, 为更加准确地了解重金属污染状况, 应使用IDW法或RBF法进行插值运算.
(3) 地累积指数污染评价显示, 研究区As含量超标样点占5.5%, Cd含量超标样点占99.0%.采用不同污染程度地累积指数所对应的Cd含量作为阈值, Cd轻度-中度程度污染范围分布较广, 中度-强污染程度以上的高概率污染区域主要位于研究区的中部.
致谢: 感谢国土资源部生态地球化学重点实验室提供的资助.| [1] |
龚梦丹, 朱维琴, 顾燕青, 等. 杭州蔬菜基地重金属污染及风险评价[J]. 环境科学, 2016, 37(6): 2329-2337. Gong M D, Zhu W Q, Gu Y Q, et al. Evaluation on heavy metal pollution and its risk in soils from vegetable bases of Hangzhou[J]. Environmental Science, 2016, 37(6): 2329-2337. |
| [2] |
张红桔, 赵科理, 叶正钱, 等. 典型山核桃产区土壤重金属空间异质性及其风险评价[J]. 环境科学, 2018, 39(6): 2893-2903. Zhang H J, Zhao K L, Ye Z Q, et al. Spatial variation of heavy metals in soils and its ecological risk evaluation in a typical Carya cathayensis production area[J]. Environmental Science, 2018, 39(6): 2893-2903. |
| [3] |
周艳, 陈樯, 邓绍坡, 等. 西南某铅锌矿区农田土壤重金属空间主成分分析及生态风险评价[J]. 环境科学, 2018, 39(6): 2884-2892. Zhou Y, Chen Q, Deng S P, et al. Principal component analysis and ecological risk assessment of heavy metals in farmland soils around a Pb-Zn mine in Southwestern China[J]. Environmental Science, 2018, 39(6): 2884-2892. |
| [4] |
吴洋, 杨军, 周小勇, 等. 广西都安县耕地土壤重金属污染风险评价[J]. 环境科学, 2015, 36(8): 2964-2971. Wu Y, Yang J, Zhou X Y, et al. Risk assessment of heavy metal contamination in farmland soil in Du'an autonomous county of Guangxi Zhuang autonomous region, China[J]. Environmental Science, 2015, 36(8): 2964-2971. |
| [5] |
刘硕, 吴泉源, 曹学江, 等. 龙口煤矿区土壤重金属污染评价与空间分布特征[J]. 环境科学, 2016, 37(1): 270-279. Liu S, Wu Q Y, Cao X J, et al. Pollution assessment and spatial distribution characteristics of heavy metals in soils of coal mining area in Longkou city[J]. Environmental Science, 2016, 37(1): 270-279. |
| [6] |
周建军, 周桔, 冯仁国. 我国土壤重金属污染现状及治理战略[J]. 中国科学院院刊, 2014, 29(3): 315-320, 350. Zhou J J, Zhou J, Feng R G. Status of China's heavy metal contamination in soil and its remediation strategy[J]. Bulletin of Chinese Academy of Sciences, 2014, 29(3): 315-320, 350. |
| [7] |
龙军, 张黎明, 沈金泉, 等. 复杂地貌类型区耕地土壤有机质空间插值方法研究[J]. 土壤学报, 2014, 51(6): 1270-1281. Long J, Zhang L M, Shen J Q, et al. Spatial interpolation of soil organic matter in farmlands in areas complex in landform[J]. Acta Pedologica Sinica, 2014, 51(6): 1270-1281. |
| [8] |
于伟宣, 赵明松, 王萌, 等. 采样数量与空间插值方法对土壤属性预测精度的影响[J]. 科学技术与工程, 2017, 17(25): 186-191. Yu W X, Zhao M S, Wang M, et al. Effects of sampling sizes and spatial interpolation methods on prediction accuracy of soil properties[J]. Science Technology and Engineering, 2017, 17(25): 186-191. DOI:10.3969/j.issn.1671-1815.2017.25.030 |
| [9] |
李凯, 赵华甫, 吴克宁, 等. 土壤重金属Cd污染指数的适宜插值方法和合理采样数量研究[J]. 土壤通报, 2016, 47(5): 1056-1064. Li K, Zhao H P, Wu K N, et al. Suitable interpolation method and reasonable sampling quantity of Cd pollution index in soil[J]. Chinese Journal of Soil Science, 2016, 47(5): 1056-1064. |
| [10] |
陈思萱, 邹滨, 汤景文. 空间插值方法对土壤重金属污染格局识别的影响[J]. 测绘科学, 2015, 40(1): 63-67. Chen S X, Zou B, Tang J W. Impact of spatial interpolation methods on identifying structure of heavy metal polluted soil[J]. Science of Surveying and Mapping, 2015, 40(1): 63-67. |
| [11] |
张金兰, 欧阳婷萍, 黄铁兰, 等. 农田表层土壤镉的典型空间插值方法对比研究[J]. 生态科学, 2017, 36(6): 130-136. Zhang J L, Ouyang T P, Huang T L, et al. Comparison of typical interpolation methods for spatial distribution of Cd in soil[J]. Ecological Science, 2017, 36(6): 130-136. |
| [12] |
李湘凌, 张颖慧, 杨善谋, 等. 合肥义城地区土壤重金属污染评价中典型插值方法的对比[J]. 吉林大学学报(地球科学版), 2011, 41(1): 222-227. Li X L, Zhang Y H, Yang S M, et al. Comparison of typical interpolation methods for pollution evaluation of soil heavy metals in Yicheng district, Hefei[J]. Journal of Jilin University (Earth Science Edition), 2011, 41(1): 222-227. |
| [13] |
杨奇勇, 谢运球, 罗为群, 等. 基于地统计学的土壤重金属分布与污染风险评价[J]. 农业机械学报, 2017, 48(12): 248-254. Yang Q Y, Xie Y Q, Luo W Q, et al. Spatial distribution and soil pollution risk evaluation of soil heavy metals content based on geostatistics[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(12): 248-254. DOI:10.6041/j.issn.1000-1298.2017.12.029 |
| [14] |
张慧, 郑志志, 马鑫鹏, 等. 哈尔滨市土壤表层重金属污染特征及来源辨析[J]. 环境科学研究, 2017, 30(10): 1597-1606. Zhang H, Zhen Z Z, Ma X P, et al. Sources and pollution characteristics of heavy metals in surface soils of Harbin city[J]. Research of Environmental Sciences, 2017, 30(10): 1597-1606. |
| [15] | Chu H J, Lin Y P, Jang C S, et al. Delineating the hazard zone of multiple soil pollutants by multivariate indicator Kriging and conditioned Latin hypercube sampling[J]. Geoderma, 2010, 158(3-4): 242-251. DOI:10.1016/j.geoderma.2010.05.003 |
| [16] | DZ/T 0295-2016土地质量地球化学评价规范[S]. |
| [17] | 汤国安, 杨昕. ArcGIS地理信息系统空间分析实验教程[M]. 北京: 科学出版社, 2006: 363-421. |
| [18] |
谢云峰, 陈同斌, 雷梅, 等. 空间插值模型对土壤Cd污染评价结果的影响[J]. 环境科学学报, 2010, 30(4): 847-854. Xie Y F, Chen T B, Lei M, et al. Impact of spatial interpolation methods on the estimation of regional soil Cd[J]. Acta Scientiae Circumstantiae, 2010, 30(4): 847-854. |
| [19] | 张仁铎. 空间变异理论及应用[M]. 北京: 科学出版社, 2005: 23-39. |
| [20] | Davis B M. Uses and abuses of cross-validation in geostatistics[J]. Mathematical Geology, 1987, 19(3): 241-248. DOI:10.1007/BF00897749 |
| [21] |
付传城, 王文勇, 潘剑君, 等. 南京市溧水区土壤重金属污染不同插值方法的对比研究[J]. 土壤通报, 2014, 45(6): 1325-1333. Fu C C, Wang W Y, Pan J J, et al. A comparative study on different soil heavy metal interpolation methods in Lishui district, Nanjing[J]. Chinese Journal of Soil Science, 2014, 45(6): 1325-1333. |
| [22] |
史文娇, 岳天祥, 石晓丽, 等. 土壤连续属性空间插值方法及其精度的研究进展[J]. 自然资源学报, 2012, 27(1): 163-175. Shi W J, Yue T X, Shi X L, et al. Research progress in soil property interpolators and their accuracy[J]. Journal of Natural Resources, 2012, 27(1): 163-175. |
| [23] |
缐东红, 缐春媚. 基于地累积和生态风险指数法评价索尔奇湿地公园土壤重金属污染状况[J]. 北方农业学报, 2017, 45(4): 68-72. Xian D H, Xian C M. Based on the land accumulation and ecological risk index method evaluating heavy metal pollution situation of Sorci Wetland Park[J]. Journal of Northern Agriculture, 2017, 45(4): 68-72. DOI:10.3969/j.issn.2096-1197.2017.04.14 |
| [24] |
张菊, 陈振楼, 许世远, 等. 上海城市街道灰尘重金属铅污染现状及评价[J]. 环境科学, 2006, 27(3): 3519-3523. Zhang J, Chen Z L, Xu S Y, et al. Lead pollution and its assessment in urban street dust of Shanghai[J]. Environmental Science, 2006, 27(3): 3519-3523. |
| [25] | 国家环境保护局. 中国土壤元素背景值[M]. 北京: 中国环境科学出版社, 1990: 330-493. |
| [26] |
姜菲菲, 孙丹峰, 李红, 等. 北京市农业土壤重金属污染环境风险等级评价[J]. 农业工程学报, 2011, 27(8): 330-337. Jiang F F, Sun D F, Li H, et al. Risk grade assessment for farmland pollution of heavy metals in Beijing[J]. Transactions of the Chinese Society of Agricultural Engineering, 2011, 27(8): 330-337. DOI:10.3969/j.issn.1002-6819.2011.08.058 |
| [27] |
高玉蓉, 许红卫, 周斌. 稻田土壤养分的空间变异性研究[J]. 土壤通报, 2005, 36(6): 822-825. Gao Y R, Xu H W, Zhou B. Investigation on spatial variability of soil nutrients in paddy field[J]. Chinese Journal of Soil Science, 2005, 36(6): 822-825. DOI:10.3321/j.issn:0564-3945.2005.06.002 |
| [28] |
柳云龙, 章立佳, 韩晓非, 等. 上海城市样带土壤重金属空间变异特征及污染评价[J]. 环境科学, 2012, 33(2): 599-605. Liu Y L, Zhang L J, Han X F, et al. Spatial variability and evaluation of soil heavy metal contamination in the urban-transect of Shanghai[J]. Environmental Science, 2012, 33(2): 599-605. |
| [29] |
袁峰, 白晓宇, 周涛发, 等. 元素空间分布插值方法的对比研究:以铜陵地区土壤中的重金属元素为例[J]. 地学前缘, 2008, 15(5): 103-109. Yuan F, Bai X Y, Zhou T F, et al. Comparison between methods for interpolation of studying spatial distribution of elements:a case study of soil heavy metals in Tongling area, south China[J]. Earth Science Frontiers, 2008, 15(5): 103-109. DOI:10.3321/j.issn:1005-2321.2008.05.012 |
| [30] | Cambardella C A, Moorman T B, Parkin T B, et al. Field-scale variability of soil Properties in central Iowa soils[J]. Soil Science Society of America Journal, 1994, 58(5): 1501-1511. DOI:10.2136/sssaj1994.03615995005800050033x |
| [31] |
秦玮, 何方, 范贵娟, 等. 不同插值方法对土壤养分空间插值结果的影响——以寿西湖农场为例[J]. 安徽农学通报, 2017, 23(19): 51-53. Qin W, He F, Fan G J, et al. Effects of different interpolation methods on spatial interpolation of soil nutrients-taking Shouxihu farm as an example[J]. Anhui Agricultural Science Bulletin, 2017, 23(19): 51-53. DOI:10.3969/j.issn.1007-7731.2017.19.027 |
| [32] | Xie Y F, Chen T B, Lei M, et al. Spatial distribution of soil heavy metal pollution estimated by different interpolation methods:accuracy and uncertainty analysis[J]. Chemosphere, 2011, 82(3): 468-476. DOI:10.1016/j.chemosphere.2010.09.053 |
| [33] |
李庆谋. 多维分形克里格方法[J]. 地球科学进展, 2005, 20(2): 248-256. Li Q M. Multifractal-krige interpolation method[J]. Advances in Earth Science, 2005, 20(2): 248-256. DOI:10.3321/j.issn:1001-8166.2005.02.016 |
| [34] |
孙慧, 郭治兴, 郭颖, 等. 广东省土壤Cd含量空间分布预测[J]. 环境科学, 2017, 38(5): 2111-2124. Sun H, Guo Z X, Guo Y, et al. Prediction of distribution of soil Cd concentrations in Guangdong province, China[J]. Environmental Science, 2017, 38(5): 2111-2124. |
 2018, Vol. 39
2018, Vol. 39


