2. 山西大学环境与资源学院, 太原 030006;
3. 太原市环境监测中心站, 太原 030002
2. College of Environmental & Resource Sciences, Shanxi University, Taiyuan 030006, China;
3. Taiyuan Environment Monitoring Central Station, Taiyuan 030002, China
大气污染物严重危害人体健康和生活环境, 因此大气污染物浓度预测问题成为近年来的研究热点.随着对空气质量恶化担忧的增加, PM10(particular matter less than 10 μm)于1996年纳入我国《环境空气质量标准》(GB 3095-1996) 作为空气质量评价的主要污染物. PM10是指空气中能够悬浮且不易沉降的固体和液体的混合物.由于大气污染物PM10直径小于10 μm, 极易进入呼吸道并沉积于肺部, 因此有极大可能引起严重的呼吸道疾病和心血管疾病, 对人体造成很大伤害[1].在其组成成分方面, PM10主要是由有机物、粉尘、SIA(secondary inorganic aerosols)、微量金属元素TMs(trace metals)、水分和未知化合物组成[2].对于PM10污染物浓度进行预测研究, 并依据预测结果对可能出现的严重空气污染事件进行科学预警是目前对空气质量研究的重点也是公众关注的热点.目前大气污染物浓度预测方法主要有统计模型和确定性模型两类[3].非线性回归、人工神经网络(artificial neural network, ANN)和支持向量机(support vector machine, SVM)等模型已成功地应用于空气污染物预测问题[4~6]. Perez等[4]将ANN模型应用于PM2.5小时浓度预测, 表现出良好的预测能力. Zhang等[5]使用ANN分析了太原市PM10浓度特征并建立预测模型. Sun等[6]通过实验验证了基于LSSVM的PM2.5预测模型能有效应用于大气污染物浓度预测.统计模型适合于描述大气污染物浓度与影响污染物浓度的相关因素之间的复杂非线性关系, 因此具有较好的预测精度, 并且预测系统结构简单, 运行效率较高[3].近年来随着数据挖掘技术的发展, ANN和SVM成功应用于PM10时序数据的预测, 其中ANN存在局部最优和过拟合的问题[7], 而SVM基于统计学习理论, 以结构风险最小化为目标[8], 克服了过拟合和局部最优的问题[9], 在污染物浓度预测研究中表现出良好的泛化能力[10, 11].确定性模型依据边界层气象数据、污染源信息和污染物复杂的物理化学形成过程, 模拟污染物的释放、累积或扩散过程[12, 13], 因此预测系统需要网格状气象、排放源和化学ICONs和BCONs数据等信息.此类预测系统实现复杂且需较长的系统运行时间, 并且模型的精度在很大程度上依赖于系统所需的复杂数据信息[14].
PM10是太原城区的主要大气污染物, 其来源复杂, 可以来源于自然环境, 也与人类活动有密切联系, 尤其在城市地区, 主要来源有机动车尾气、工业过程和化石燃料燃烧等方面[15].污染物PM10的浓度受到排放源、气象条件和复杂下垫面等多种因素的影响, 并且PM10为混合污染物, 与复杂物理化学过程相关[16, 17], 因此PM10时序数据具有高度复杂性、非线性等特征[18, 19]. PM10的浓度特征随时间变化, 可以认为PM10浓度变化是一个非线性动态系统[16, 17].因此在PM10浓度预测过程中很难准确确定污染源信息, 并且受到监测站点设置等因素制约, 与PM10浓度相关的外生影响因素(例如:排放源、气象数据、地形特征、其它相关污染物浓度等)数据亦很难获取, 大多情况下人们得到的研究数据仅仅是一维PM10浓度时间序列数据.在这种数据信息不完备、无法采用高级物理模型进行预测的情况下, 如何快速、准确得到PM10预测结果, 是非常重要并且具有现实意义的.
本文使用wavelet模型对PM10污染物浓度时序数据进行小波分析得到高维时频信息, 该信息作为SVM输入向量建立wavelet-SVM模型.并以山西省太原市4个空气质量监测站点的PM10浓度数据为研究对象, 完成以下研究目标:① 分析太原市城区PM10污染物浓度的时空分布特点; ② 通过小波变换将PM10浓度时序数据分解为高频信息和低频信息, 挖掘数据潜在信息, 重构数据结构; ③ 建立wavelet-SVM污染物浓度预测模型; ④ 将传统SVM预测结果、wavelet-SVM预测结果与实测PM10浓度数据进行比较, 验证通过wavelet将PM10浓度数据变换为高维时频信息的wavelet-SVM预测模型具有较好的泛化能力, 同时算法设计简单, 具有很好的实用性.
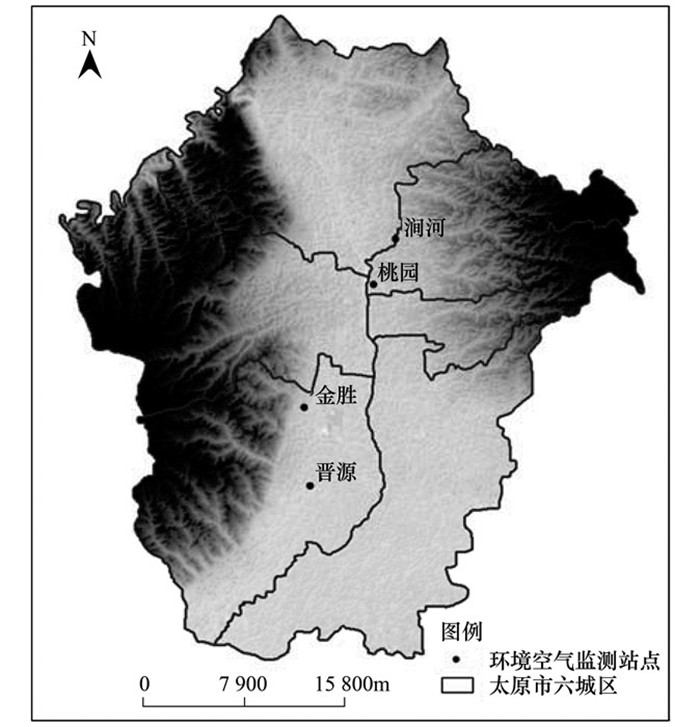
1 材料与方法 1.1 研究区域太原位于中国中部(111°30′~113°09′E; 37°27′~38°25′N), 山西省省会, 总面积6 988 km2, 人口429.89万.太原市区地形为西、北和东三面环山, 中部和南部为平原, 形成天然的簸箕形, 该地形特征将增加大气污染物累积效应.此外, 太原作为中国能源、重工业基地之一, 并且以煤炭为主要能源, 因此, PM10是太原地区大气污染物中的主要污染物. 图 1为太原地区数字高程模型(digital elevation model, DEM).
|
图 1 太原市区空气质量监测站点 Fig. 1 Location of air quality monitoring stations and DEM of Taiyuan |
PM10浓度数据来源于太原市环境监测中心站, 监测站点包括太原市城区晋源、桃园、涧河和金胜4个环境监测站点, 如图 1所示.实验数据集由2013年1月1日~2013年12月31日, PM10浓度数据为日平均值, 共计365组数据.其中2013年1月1日~2013年9月31日的273组数据为训练数据, 2013年10月1日~2013年12月31日的92组数据作为测试数据.
1.3 研究方法目前SVM应用于PM10浓度时序预测表现出良好的预测精度. SVM模型通过核函数很好地表示输入向量与预测目标之间的高维非线性关系, 合适的高维输入向量将有效、准确描述信息特征, 表达数据含义, 因此模型预测能力在很大程度上依赖于模型设计中输入向量的选择. SVM在处理一维时序数据时通常选择历史数据作为输入向量, 输入向量维度较低, 无法体现SVM模型高维非线性特征, 在一定程度上影响模型的泛化能力.因此, 在采用SVM模型对PM10时序数据进行预测时, 为获得更高的预测精度, 可对输入向量(PM10时序数据)进行结构变换, 将一维数据升维成高维数据, 更加全面、有效地表示数据变化趋势, 从而提高预测精度. PM10污染物浓度时序数据{y1, y2, …, yl}可被认为是一组信号序列, 由于小波分析适用于这种非线性非平稳时序数据, 因此可将该方法应用于分析提取大气污染物浓度时序数据在不同时频上的信息特征.小波变换通过窗口调整, 对信号伸缩平移运算进行局部化分析, 将输入信号分解成能够真正反映信号数据真实变化趋势的低频信号和随机扰动的高频信号[20~22].通过小波变换将污染物浓度数据分解为由不同组成部分构成的序列组, 这些子序列相较于原数据具有更稳定的方差和较少的奇异值点, 能更有效、准确地表达原信号信息, 因此预测准确性更好[23].若小波变换的尺度函数为φ(t), 母小波函数为ψ(t)则:
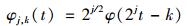
|
(1) |
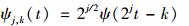
|
(2) |
式中j和k分别为尺度参数及平移参数.信号y(t)由公式(1) 和(2) 可表示为:
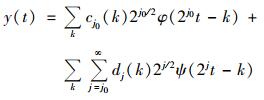
|
(3) |
式中,cj0(k)和dj(k)分别为近似系数及细节系数.污染物浓度数据通过m步小波变换可分解为:
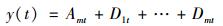
|
式中, Amt为近似信息代表原信息特征, D1t…Dmt为高频信息表示细微信号波动即原信息的噪声部分[24].由小波变换分解得到的低频近似信息和高频信息构成新的预测数据集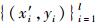
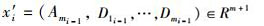
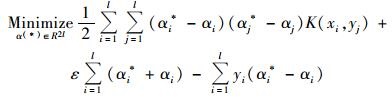
|
(4) |
约束于:
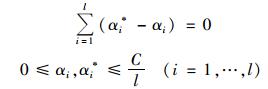
|
式中, αi, αi*是Lagrange乘子, 并且对应非零(αi, αi*)的数据称为支持向量, K(xi, xj)=φ(xi)·φ(xj)为核函数, 则目标函数为:
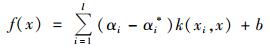
|
(5) |
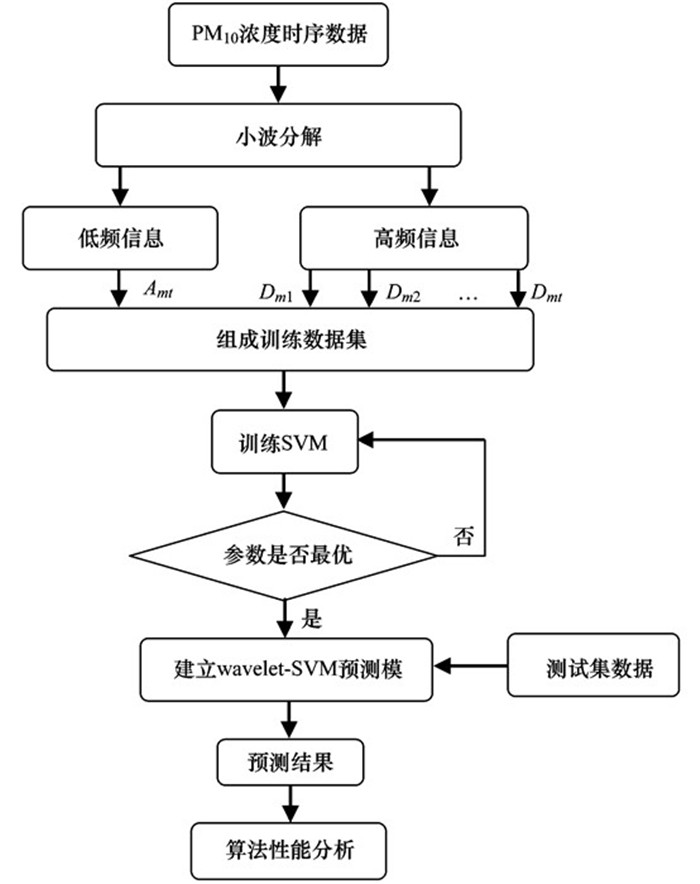
图 2给出了wavelet-SVM预测模型的构建过程.
|
图 2 wavelet-SVM预测模型流程示意 Fig. 2 Process of wavelet-SVM forecasting model |
以上基于小波变换的wavelet-SVM预测模型可描述如下:
输入:训练数据集{(Xi, Yi)}i=1t, 其中Xi=PM10i-1, 及t+1时刻输入向量Xt+1=PM10t.
输出:t+1时刻PM10污染物预测浓度Y.t+1
Step1:由PM10浓度数据形成时序数据集{PM101, PM102, …, PM10t}, 使用小波变换, PM10浓度时序数据经过m层分解可得到高维输入信息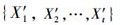
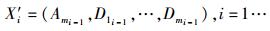
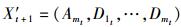
Step2:根据前一步中得到的高维输入信息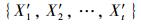
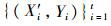
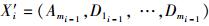
Step3:在新得到的训练集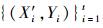
Step4:使用以上学习得到的预测模型及根据Step1中得到的t+1期输入向量X′t+1=(Amt, D1t, …, Dmt), 可预测得到t+1期PM10浓度的预测值f(X′t+1).
通过重复步骤Step1~Step4将得到预测值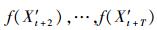
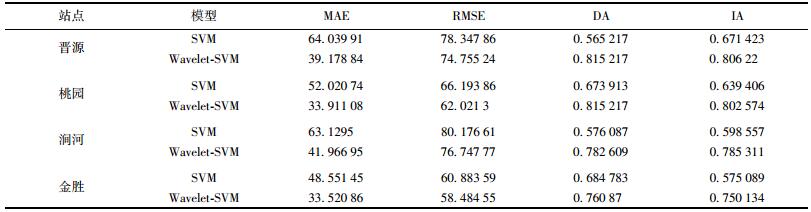
为验证本文提出的基于小波变换的wavelet-SVM预测模型的有效性, 选择MAE (the mean absolute error)、RMSE (the root mean square error)、DA(direction accuracy)和IA (index of agreement)作为衡量算法性能的指标.通常, 较好的预测模型具有较小的MAE和RMSE. DA代表预测模型对于时序数据方向变化的预测能力, 较大的DA拥有较准确的方向预测结果.模型有较大的IA反映了预测结果与实际值更接近[24].以上算法性能指标既从模型预测精度方面评价模型泛化能力, 也从时序数据趋势变化预测方面给出衡量标准, 可以全面评价模型预测能力.
2 结果与分析为验证本文提出的wavelet-SVM预测模型相较于传统SVM模型是否能有效提高预测精度, 笔者分别对太原4个站点的预测结果进行了比较.实验中预测模型由Matlab 7.0及Weka 3软件设计完成.模型中相关参数选择以MAE最小为目标.小波分解选用Daubechies(db)小波基函数, Daubechies具有低通和高通滤波性质, 适宜于特征提取, 并且具有内在正交性, 满足Parsaval理论[25], 在时序数据分析应用中, Daubechies小波取得广泛应用并表现出良好的性能[26~28].
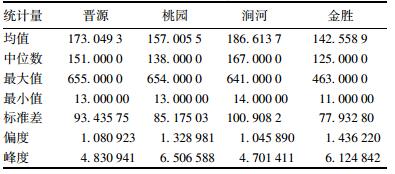
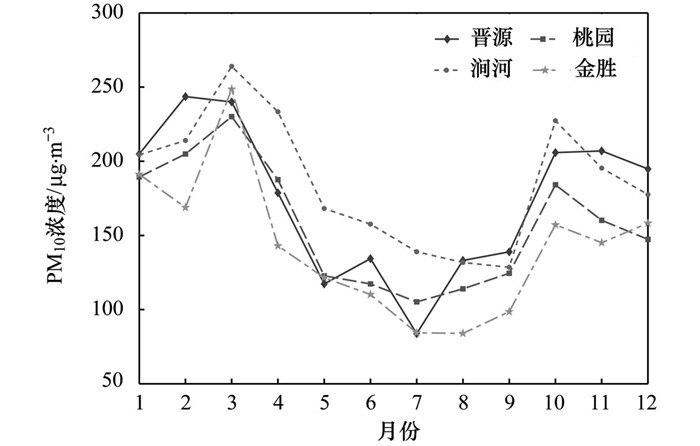
2.1 太原城区PM10浓度时空分析本文收集了太原市城区4个环境监测站点获得的2013年全年PM10日浓度数据, 表 1给出了4个站点数据的描述统计结果, 图 3为以上4个站点月平均PM10浓度时序.从月尺度的PM10浓度变化趋势可看出, 晋源、桃园、涧河和金胜站点全年PM10浓度变化趋势基本一致(图 3), 其中1、2、3、11和12月PM10浓度有明显升高, 主要原因是冬季采暖增加了PM10排放总量.在以上4个站点中PM10浓度的最大值为655 μg·m-3, 2013年2月25日出现于晋源站点, 其余站点的PM10浓度的最大值也均出现于冬季. PM10浓度的最小值为11 μg·m-3, 出现在7月11日金胜站点, 4站点PM10浓度的最小值都出现在7月, 太原城区夏季PM10浓度相较于冬季维持较低水平.由表 1可以看出, 本研究的4个站点中, 晋源和涧河站点PM10浓度较高, 而桃园和金胜站点PM10浓度较低, 均值和标准差的值较小.从图 3月均浓度走势可看出, 4站点中金胜站点PM10浓度月平均值略低其他站点, 然而全年PM10浓度仍处于较高水平.
|
|
表 1 PM10浓度数据统计指标结果/μg·m-3 Table 1 Statistical indicators of PM10 concentrations/μg·m-3 |
|
图 3 PM10月平均浓度 Fig. 3 Monthly mean concentrations of PM10 |
从空间位置来看, 以上站点较均匀分布于太原城区, 可以全面分析太原城区PM10浓度分布情况.晋源站点距离市区较远, 非采暖季PM10浓度保持较低水平, 冬季及早春燃煤采暖增加PM10排放.桃园站点位于居民生活区, PM10主要来源于机动车排放、地面扬尘等.涧河站点周边机动车数量密集, 机动车尾气排放是PM10的主要来源.金胜站点位于工业区, 紧邻太原第一热电厂, PM10主要来源于工业排放.
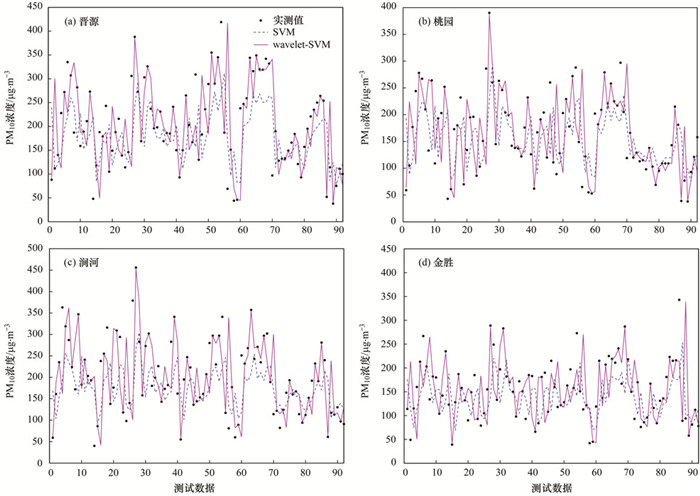
2.2 基于SVM模型的太原城区PM10预测SVM模型应用于太原城区4个站点PM10浓度预测结果如图 4, 其中虚线为SVM模型预测结果, 预测样本由2013年10月1日~2013年12月31日, 共包含92个测试样本, 图 5为预测结果的散点图, 表 2给出预测模型性能指标. SVM预测模型的算法性能指标MAE和RMSE较小, 在只有PM10浓度历史数据的情况下, 能比较好地完成短期预测任务.然而由图 4可以看出, 当预测目标波动较大时, 预测模型的预测结果与实际值误差较大, 也就是说, 无法有效跟踪到大气污染物浓度的突变点, 对于突发污染事件预警有一定难度.并且方向指标DA值比较小, 其中晋源和涧河站点DA分别只有0.565 217和0.576 087, 桃园和金胜站点的DA也都小于0.7, SVM模型对于PM10浓度方向趋势预测效果不够准确, 不能提供准确、有效的污染物浓度变化方向的判断依据.此外由SVM预测模型得到的IA值也较小, 表示预测结果与真值一致性较差. SVM预测模型作为高维非线性模型, 应用于大气污染物时序预测问题时, 输入向量只包含污染物历史数据, 这样的数据形式不能有效描述预测目标, 在一定程度上影响了模型预测能力.
|
图 4 SVM模型与wavelet-SVM模型对PM10浓度预测结果时序图 Fig. 4 Time-series plots of SVM and wavelet-SVM forecasts for PM10 concentrations |
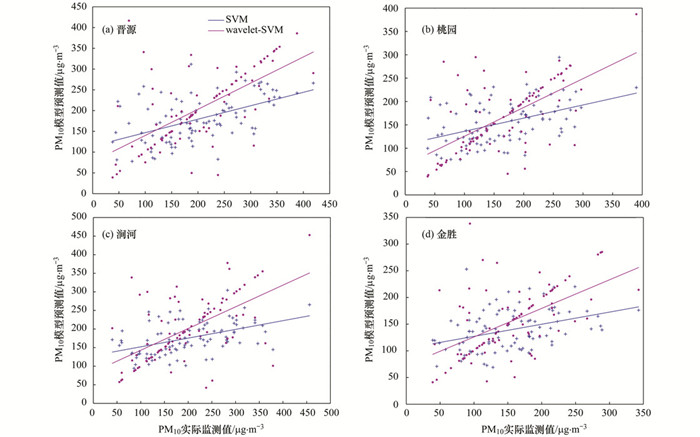
|
图 5 SVM模型与wavelet-SVM模型PM10浓度预测结果散点图 Fig. 5 Scatterplots of SVM and wavelet-SVM forecasts for PM10 concentrations |
|
|
表 2 模型预测性能比较结果 Table 2 Forecasting accuracy of SVM and wavelet-SVM |
2.3 基于wavelet-SVM模型的太原城区PM10预测
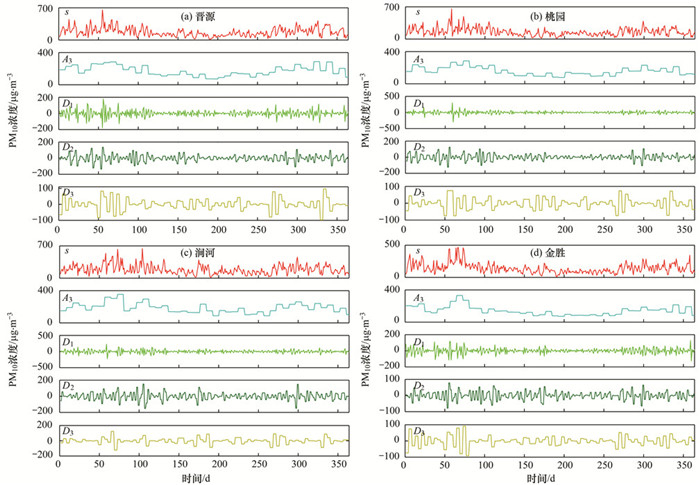
在wavelet-SVM预测模型中, PM10浓度时序数据由db1小波经过3层分解后得到训练数据集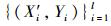
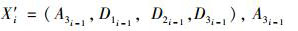
|
图 6 PM10数据小波分解结果 Fig. 6 Decomposition sequences of the original PM10 concentration data |
由图 4给出的wavelet-SVM模型预测结果可以看出, wavelet-SVM模型得到的太原市城区4个不同监测站点的预测结果都可以很好地拟合PM10的真实值, 尤其是当PM10浓度值较大时, wavelet-SVM模型也能获得较满意的预测结果. 表 2给出的模型性能指标MAE和RMSE值较小, 表明模型预测精度较高. DA的值较大, 模型对于PM10的方向趋势预测较准确.模型算法性能指标表明wavelet-SVM模型具有较好的泛化能力.
2.4 SVM模型与wavelet-SVM模型预测结果比较预测模型SVM和wavelet-SVM的预测结果与观测值如图 4显示.分析分别由SVM和wavelet-SVM预测得到的结果, 从时序图中可以看出对于4个监测站点的数据, 本文提出的模型的预测结果更加接近真实值, 也就是说wavelet-SVM具有更好的预测精度. 图 5为观测值和模型预测值的散点图, 分别对4个站点SVM和wavelet-SVM预测结果进行了比较, 其中直线分别为以上SVM和wavelet-SVM两个预测模型预测结果的回归结果, 可以得出结论wavelet-SVM具有更好的回归结果, 有效提高了模型泛化能力.为更加全面评价模型性能, 在表 2中给出了模型性能的统计值MAE、RMSE、DA和IA.可以从表 2看出wavelet-SVM预测模型在这4项算法性能评价指标上有明显改善, 例如晋源站点MAE和RMSE由原先的64.03991, 78.347 86降低为39.178 84和74.75524, 其中MAE降低了38.8%, 预测精度有明显提高.并且DA和IA分别由0.565 217、0.671 423显著提高到0.815 217和0.806 22, 其中DA值提高尤为明显, wavelet-SVM模型具有更加准确的时序数据方向预测能力.并且由表 2可以看出对于4个监测站点数据, wavelet-SVM模型有效降低MAE值, 预测精度相较于传统SVM有较大提高.同时DA指标也有非常明显的提高, 也就是说该模型能更加有效预测PM10浓度的变化趋势, 对于空气污染物控制工作具有有效的指导作用.因此, 总的来说本文提出的wavelet-SVM预测模型能有效预测PM10浓度, 并且具有较强的鲁棒性.
3 讨论 3.1 太原市城区污染特征由太原城区4个大气污染物监测站点2013年全年PM10的日浓度数据可以看出, 太原城区PM10浓度全年变化较明显, 采暖季PM10浓度有明显升高, 然而不能否认的是, 太原城区全年PM10污染物浓度保持较高水平, 因此对于PM10污染物的防治是大气治理工作的重点.可以从以下3个方面防治大气污染:① 太原作为以煤炭为主要能源的城市, 大气污染物主要为煤烟型, 颗粒物中Ca2+和Mg2+含量与煤燃烧排放关系密切[29], 因此应进一步优化和改善能源结构, 提高清洁能源比例, 增加集中供热覆盖区域, 做好燃煤污染控制工作. ② 城市建筑方面需符合建筑节能标准, 增加城市植被和水面覆盖比例调节城市气候、改善城市大气环境.提高城市道路交通负载能力, 改善市区道路系统, 进一步提高公共交通服务质量, 鼓励新能源车推广, 控制机动车尾气污染. ③ 落实工业污染减排任务, 更新能源消耗型企业工业技术, 提高能源利用率, 控制工业烟尘排放, 核定重点企业的二氧化硫排放总量, 减少工业污染.
3.2 wavelet-SVM模型输入向量wavelet-SVM预测模型的输入向量由PM10浓度时序数据经过wavelet变换生成高维输入向量, 有效增加数据表示信息, 并且预测模型的预测精度有显著提高.太原地区三面环山, 气象条件在不同区域有一定的差别, 并且气象因素对于污染物的累积和扩散影响比较明显.若在数据可获取情况下, wavelet-SVM预测模型输入数据中加入气象信息, 更加准确表示环境状态条件, 将在很大程度上有助于提高模型泛化能力.
4 结论(1) 支持向量机作为高维非线性学习算法用于PM10污染物浓度时序数据预测取得了很好的效果, 然而由于一维时序数据信息表示不完整, 一定程度上制约了预测模型的泛化能力.
(2) wavelet-SVM预测模型使用wavelet分解PM10浓度时序数据, 构造新的高维特征向量来表达PM10浓度时序数据在不同频率下的相关信息, 更好地表示数据信息.
(3) PM10浓度时序数据通过小波变换生成适合SVM预测模型的高维输入向量, 与传统SVM模型相比需要增加一定的计算代价, 然而本文旨在数据信息获取有限, 样本容量较小情况下进一步提高预测模型的预测精度, 本文提出的模型所需数据容量小, 小波变换计算简单, 模型增加的运行时间非常有限.
(4) 实验数据揭示了一年期内太原市城区PM10污染物浓度变换特征, 接近工业排放源或市区中心机动车较密集区域PM10浓度较高, 并且进入采暖期后污染物浓度明显提高.
(5) 由实验结果可看出wavelet-SVM模型对于预测精度有显著提高, 尤其是对于污染物浓度变化较大的数据点, wavelet-SVM模型能更好地预测污染物浓度突变情况, 因此可以认为污染物浓度时序数据经小波变换后得到的由低频信息和高频信息组成的高维输入向量对数据信息表达更加准确、有效.在不同数据集上的实验结果证明该模型很好地挖掘出了大气污染物浓度时序数据与预测目标相关的输入特征, 并且在与传统SVM预测模型的比较中, 表现出良好的预测精度和稳定性, 同时该方法设计简单, 具有较强的实用性.本文的研究结果不仅能有效应用于PM10浓度时序数据预测, 同时也可用于其他污染物的时序预测研究, 为相关部门进行大气污染防治和突发污染事件应急管理提供理论支持和决策依据.
| [1] |
张南, 熊黑钢, 葛秀秀, 等. 北京市冬季雾霾天人体呼吸高度PM2.5变化特征对气象因素的响应[J]. 环境科学, 2016, 37(7): 2419-2426. Zhang N, Xiong H G, Ge X X, et al. Response of human respiratory height PM2.5 variation characteristics to meteorological factors during winter haze days in Beijing[J]. Environmental Science, 2016, 37(7): 2419-2426. |
| [2] | Li P Z, Wang Y, Dong Q L. The analysis and application of a new hybrid pollutants forecasting model using modified Kolmogorov-Zurbenko filter[J]. Science of the Total Environment, 2017, 583: 228-240. DOI:10.1016/j.scitotenv.2017.01.057 |
| [3] | Zhang Y, Bocquet M, Mallet V, et al. Real-time air quality forecasting, Part Ⅰ: history, techniques, and current status[J]. Atmospheric Environment, 2012, 60: 632-655. DOI:10.1016/j.atmosenv.2012.06.031 |
| [4] | Perez P, Gramsch E. Forecasting hourly PM2.5 in Santiago de Chile with emphasis on night episodes[J]. Atmospheric Environment, 2016, 124: 22-27. DOI:10.1016/j.atmosenv.2015.11.016 |
| [5] | Zhang H, Liu Y, Shi R, et al. Evaluation of PM10 forecasting based on the artificial neural network model and intake fraction in an urban area: a case study in Taiyuan City, China[J]. Journal of the Air & Waste Management Association, 2013, 63(7): 755-763. |
| [6] | Sun W, Sun J Y. Daily PM2.5 concentration prediction based on principal component analysis and LSSVM optimized by cuckoo search algorithm[J]. Journal of Environmental Management, 2017, 188: 144-152. DOI:10.1016/j.jenvman.2016.12.011 |
| [7] | Cao L J. Support vector machines experts for time series forecasting[J]. Neurocomputing, 2003, 51: 321-339. DOI:10.1016/S0925-2312(02)00577-5 |
| [8] | Pai P F, Lin K P, Lin C S, et al. Time series forecasting by a seasonal support vector regression model[J]. Expert Systems with Applications, 2010, 37(6): 4261-4265. DOI:10.1016/j.eswa.2009.11.076 |
| [9] | Vapnik V, Golowich S E, Smola A. Support vector method for function approximation, regression estimation, and signal processing[A]. In: Proceedings of the 9th International Conference on Neural Information Processing Systems[C]. Denver, Colorado: MIT Press, 1996. 281-287. |
| [10] | García Nieto P J, Combarro E F, del Coz Díaz J J, et al. A SVM-based regression model to study the air quality at local scale in Oviedo urban area (Northern Spain): a case study[J]. Applied Mathematics and Computation, 2013, 219(17): 8923-8937. DOI:10.1016/j.amc.2013.03.018 |
| [11] | Lin K P, Pai P F, Yang S L. Forecasting concentrations of air pollutants by logarithm support vector regression with immune algorithms[J]. Applied Mathematics and Computation, 2011, 217(12): 5318-5327. DOI:10.1016/j.amc.2010.11.055 |
| [12] | Periši Dć M, Maleti Dć D, Stoji Dć S S, et al. Forecasting hourly particulate matter concentrations based on the advanced multivariate methods[J]. International Journal of Environmental Science and Technology, 2016, 14: 1-8. |
| [13] | Chen Y Y, Shi R H, Shu S J, et al. Ensemble and enhanced PM10 concentration forecast model based on stepwise regression and wavelet analysis[J]. Atmospheric Environment, 2013, 74: 346-359. DOI:10.1016/j.atmosenv.2013.04.002 |
| [14] | Wang D Y, Wei S, Luo H Y, et al. A novel hybrid model for air quality index forecasting based on two-phase decomposition technique and modified extreme learning machine[J]. Science of the Total Environment, 2017, 580: 719-733. DOI:10.1016/j.scitotenv.2016.12.018 |
| [15] | Perez P. combined model for PM10 forecasting in a large city[J]. Atmospheric Environment, 2012, 60: 271-276. DOI:10.1016/j.atmosenv.2012.06.024 |
| [16] | Poggi J M, Portier B. PM10 forecasting using clusterwise regression[J]. Atmospheric Environment, 2011, 45(38): 7005-7014. DOI:10.1016/j.atmosenv.2011.09.016 |
| [17] | Dotse S Q, Dagar L, Petra M I, et al. Influence of Southeast Asian Haze episodes on high PM10 concentrations across Brunei Darussalam[J]. Environmental Pollution, 2016, 219: 337-352. DOI:10.1016/j.envpol.2016.10.059 |
| [18] | Zhu B Z, Wei Y M. Carbon price forecasting with a novel hybrid ARIMA and least squares support vector machines methodology[J]. Omega, 2013, 41(3): 517-524. DOI:10.1016/j.omega.2012.06.005 |
| [19] | Wang P, Liu Y, Qin Z D, et al. A novel hybrid forecasting model for PM10 and SO2daily concentrations[J]. Science of the Total Environment, 2015, 505: 1202-1212. DOI:10.1016/j.scitotenv.2014.10.078 |
| [20] | Nourani V, Baghanam A H, Adamowski J, et al. Applications of hybrid wavelet-Artificial Intelligence models in hydrology: A review[J]. Journal of Hydrology, 2014, 514: 358-377. DOI:10.1016/j.jhydrol.2014.03.057 |
| [21] |
陈亚玲, 赵智杰. 基于小波变换与传统时间序列模型的臭氧浓度多步预测[J]. 环境科学学报, 2013, 33(2): 339-345. Chen Y L, Zhao Z J. A multi-step-ahead prediction of ozone concentration using wavelet transform and traditional time series model[J]. Acta Scientiae Circumstantiae, 2013, 33(2): 339-345. |
| [22] | Alizadeh M J, Kavianpour M R. Development of wavelet-ANN models to predict water quality parameters in Hilo Bay, Pacific Ocean[J]. Marine Pollution Bulletin, 2015, 98(1-2): 171-178. DOI:10.1016/j.marpolbul.2015.06.052 |
| [23] | Li S, Wang P, Goel L. Short-term load forecasting by wavelet transform and evolutionary extreme learning machine[J]. Electric Power Systems Research, 2015, 122: 96-103. DOI:10.1016/j.epsr.2015.01.002 |
| [24] | Vlachogianni A, Kassomenos P, Karppinen A, et al. Evaluation of a multiple regression model for the forecasting of the concentrations of NOx and PM10 in Athens and Helsinki[J]. Science of the Total Environment, 2011, 409(8): 1559-1571. DOI:10.1016/j.scitotenv.2010.12.040 |
| [25] | Jazebi S, Vahidi B, Jannati M. A novel application of wavelet based SVM to transient phenomena identification of power transformers[J]. Energy Conversion and Management, 2011, 52(2): 1354-1363. DOI:10.1016/j.enconman.2010.09.033 |
| [26] | Feng X, Li Q, Zhu Y J, et al. Artificial neural networks forecasting of PM2.5 pollution using air mass trajectory based geographic model and wavelet transformation[J]. Atmospheric Environment, 2015, 107: 118-128. DOI:10.1016/j.atmosenv.2015.02.030 |
| [27] | Sun Y X, Leng B, Guan W. A novel wavelet-SVM short-time passenger flow prediction in Beijing subway system[J]. Neurocomputing, 2015, 166: 109-121. DOI:10.1016/j.neucom.2015.03.085 |
| [28] | Deo R C, Wen X H, Qi F. A wavelet-coupled support vector machine model for forecasting global incident solar radiation using limited meteorological dataset[J]. Applied Energy, 2016, 168: 568-593. DOI:10.1016/j.apenergy.2016.01.130 |
| [29] |
曹润芳, 闫雨龙, 郭利利, 等. 太原市大气颗粒物粒径和水溶性离子分布特征[J]. 环境科学, 2016, 37(6): 2034-2040. Cao R F, Yan Y L, Guo L L, et al. Distribution characteristics of water-soluble Ions in size-segregated particulate matters in Taiyuan[J]. Environmental Science, 2016, 37(6): 2034-2040. |
 2017, Vol. 38
2017, Vol. 38