2. 南京工业大学环境学院, 南京 210009
2. College of Environment, Nanjing Tech University, Nanjing 210009, China
我国现有化学物质约4.6万种,化学品的广泛使用带来了大量的环境问题. 为了防控化学品的风险,欧盟、 美国和中国都发布了化学品的管理法规,要求新化学物质在首次生产或进口前必须开展危害评估和暴露评估相结合的风险评估,我国还要求开展重点环境管理危险化学品的环境风险评估,依据风险评估的结果开展相应的管理. 暴露评估主要研究化学品的排放过程以及在环境中归趋和分布,其中污水处理厂(sewage treatment plant,STP)中化学品的归趋过程和处理效率是风险评估的重要内容,决定了化学品的暴露浓度和风险水平[1].
虽然部分化学品在污水处理厂的去除率达70%以上[2],但是由于运行工艺、 化学品性质以及处理不完全等原因,STP处理后的出水中有机化学品仍然具有显著的残留浓度(>0.1 μg ·L-1)[3, 4]. 此外,化学品在STP中还可能吸附到污泥或者挥发性进入大气,这两种过程非真正的去除,只是化学品环境受纳介质的转变,对环境仍然具有较大的风险[5].
通过实际测定的方式评估化学品在STP中的暴露通常难度很大,一方面是因为环境介质多种多样(如,水、 污泥、 大气等),实际测定费时费力,且个别的实测数据代表性也不强; 另一方面,对于新化学物质,由于还未生产和使用,无法测定其在环境中的暴露水平. 因此化学品在STP中的暴露评估主要依靠模型进行预测. 国际上针对STP的操作条件建立了不同种类化学品的STP预测模型(见表 1),如:国际水协已经建立STP中预测碳、 氮和磷归趋的活性污泥数学模型[6]; Urase等[7]、 Plósz等[8]分别构建了污水处理过程中药物、 抗生素的归趋动态预测模型; 文献[9, 10, 11, 12]构建了外源性化学品在STP中的归趋静态预测模型,SimpleTreat模型[9]和STPWIN模型[10, 11]分别被欧盟和美国用于化学品环境管理登记或风险筛查过程.
| 表 1 已有STP模型概述与分析 Table 1 Summary and Analysis of Existing STP models |
目前我国的化学管理中尚缺用于暴露评估的STP预测模型或软件,主要原因是尚无与我国化学物质环境管理要求相匹配、 与我国环境条件和STP场景特征相匹配的模型或软件. 用于风险管理的STP暴露预测模型需要遵循以下原则[1]:化学品输入参数尽可能少,且输入参数与管理要求相匹配; STP基本工艺、 暴露场景参数相对固定,具有典型代表性,可用于评估化学品的个体差异; 疑者从重的保守原则; 简单、 易用. 国际水协[3, 6, 7, 8]等建立的STP动态模型不宜用于化学品风险评估,而SimpleTreat和STPWIN等模型[9, 12]在建模过程、 输入参数、 环境条件和STP场景特征等方面都与我国存在较大差异.
STP中传统活性污泥好氧处理工艺(O型工艺),已经有近90年的历史,该工艺有机化学品去除率高、 污泥负荷高、 池容积小、 运行费用低、 稳定可靠,是我国STP工艺的重要工艺,因此根据化学品在STP中的挥发、 吸附、 降解机制,遵循STP暴露预测模型的基本原则,构建以O型工艺为基本过程的STP暴露预测模型,对评估化学品在环境中的暴露情况具有重要意义. 本研究基于O型工艺,参照我国新化学物质申报中所要求的基础数据,根据化学品的挥发、 吸附、 降解等特性,依据质量守恒和逸度理论,研究建立适用于我国的C-STP(O)暴露预测模型,以期为研究化学品在STP中的归趋及风险评估提供技术工具.
1 材料与方法1.1 模型概念图及质量守恒方程构建
O型工艺主要处理构筑物为初沉池、 曝气池、 二沉池. 化学品从含有悬浮颗粒的废水流入初沉池,停留一段时间后,一部分悬浮颗粒通过重力自然沉降为污泥并被排出,其余化学品在悬浮颗粒和水中达到分配平衡后流入曝气池; 在曝气池,由于大量污泥的存在,化学品可能发生降解,也可能因为曝气而挥发进入大气; 化学品流入二沉池后,通过重力沉降后固液分离,沉降的污泥一部分排出系统,一部分回流至曝气池以保持曝气池的污泥浓度. 未去除完全的化学品从上层清液即二级出水中流出并排入受纳水体.
为了方便计算和表示各环境相,构建了模型概念图(图 1). 将各池体拆分为水相、 悬浮颗粒相、 沉积污泥相,由于曝气池在持续的曝气过程中污泥混合比较均匀,没有沉积污泥,因此曝气池只有水相和悬浮颗粒相. STP上方空气流动比较均匀,可整体划分为气相,标记为箱1; STP与外部环境存在气、 水的流入流出过程,将外部环境单独标记为箱0. 图 1中单向箭头表示从i箱到j箱的平流过程,包括水、 水中悬浮颗粒、 空气的流动以及初沉池和二沉池污泥的去除,平流过程不可逆; 双向箭头代表相邻介质i和j间的扩散,由介质i和j的非稳态浓度驱动的,包括吸附和挥发; 假定降解过程主要发生在曝气池. 由此概念模型由9箱、 15个平流过程、 6个扩散过程和1个降解过程组成.
 | 图 1 C-STP(O)模型概念示意 Fig. 1 Conception figure of C-STP(O) model |
根据化学品风险筛查的目的,建立化学品不随时间变化的预测模型,即稳态模型足以达到目的. 稳态下,各箱质量守恒见式(1).
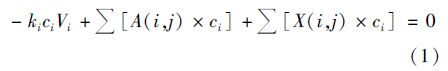
式中,ki为第i箱中生物降解一级动力学常数(s-1); ci为第i箱中化学品浓度(mol ·m-3); Vi为第i箱的体积(m3); A(i,j)为环境介质平流量(m3 ·s-1); X(i,j)为环境介质扩散流量(m3 ·s-1).
根据概念模型的9个箱体,可以写出一个九元一次的总质量守恒方程,具体见表 2. 如果A(i,j)、 X(i,j)、 c(0,2)和c(0,3)已知,解九元一次方程即可求解各箱中化学品浓度,进而计算化学品经污水处理后向大气、 地表水、 污泥的排放比例及生物降解比例.
| 表 2 总质量守恒方程矩阵 1) Table 2 Matrixes of total mass balance equation |
影响化学品在STP中归趋的参数主要有:化学品固有特性参数、 环境条件和STP场景参数. 模型应设置较少的与化学品性质相关的输入参数,符合化学品环境管理及风险筛查的要求. 为了在同一尺度下评估不同化学品的风险,模型应选择代表我国环境条件和STP工艺特征的场景参数,包括环境介质容量、 进水水质等作为模型默认值,使模型简单易用.
1.2.1 化学品固有特性参数STP模型需要污泥-水分配系数(KP,L ·kg-1)、 空气-水分配系数(KH,无量纲)及生物降解速率常数(k,s-1)等数据. SimpleTreat等模型使用吸附/解吸附系数(Koc,无量纲)或正辛醇/水分配系数(Kow,无量纲)表征化学品的吸附/解吸附,水溶解度(S,g ·L-1)、 摩尔质量(M,kg ·mol-1)、 蒸气压(P,Pa)或亨利常数(H,Pa ·m3 ·mol-1)表征挥发过程,生物降解性或生物降解半减期(DT50,d)表征生物降解过程. 我国“新化学物质环境管理办法”要求提交理化性质及环境行为等参数,包括Koc、 快速生物降解性或固有生物降解性、 S、 M、 P、 Kow,未要求提交亨利常数数据,本研究选择M、 Koc、 P、 S、 快速或固有生物降解性作为模型输入参数,其测试方法见文献[15, 16].
1.2.2 环境条件根据文献[17]2014年全国平均气温10.1℃,较常年(9.6℃)偏高0.5℃. 我国主要城市年平均风速都在1~2 m ·s-1,少数城市偏高. 温度(T)定为283 K,风速(WS)定为2 m ·s-1.
环境条件主要影响化学品的挥发过程. 蒸气压根据温度的变化,差异较大. 有必要将试验温度下的蒸气压校正到STP场景温度,校准方法根据克拉贝龙-克劳修斯方程[17].
1.2.3 STP场景参数(1)容积参数 欧盟的SimpleTreat模型使用服务人口乘以人均废水产生量、 人均固废量、 人均BOD产生量等间接数据计算STP的日处理能力和进水水质指标. 而在中国由于污水合流处理、 地域差异的影响以及数据可获得性,采用平均日处理量(Q,m3 ·d-1)、 进水悬浮固体含量和进水BOD5可简化模型并增加宜用性. 文献[19]指出,全国4 436家城镇STP,平均日处理量约为3.5万m3 ·d-1,将Q定为35 000 m3 ·d-1.
根据“室外排水设计规范”(GB 50014-2006)[20],初沉池、 曝气池、 二沉池水力停留时间(HRT)分别为2、 10、 4 h,高度(h,m)分别为4、 3、 3 m. 根据水力停留时间可计算各池体积(V,m3):V=Q×HRT/24,各池表面积(Area,m2)计算公式为Area=V/h,加和后的STP总面积(Area_STP,m2)为8 507 m2. 水体的体积为相应池体的体积,悬浮颗粒相的体积需要考虑悬浮颗粒浓度(SS,kg ·m-3)及污泥密度(RHO,kg ·L-3):V=V水×SS/(RHO×1 000); 假定沉积污泥的厚度为0.1 m,则沉积相的体积为V=0.1×Area. STP上方空气高度(hair)假定为10 m,则空气总体积V1=Area_STP×10=85 070 m3.
(2)水质和污泥参数 污水水质以及污泥性质主要影响化学品的吸附过程. 文献[21]中获得308个进水SS资料数据,均值约200 mg ·L-1,见图 2(a); 281个进水BOD5资料数据,均值约150 mg ·L-1,见图 2(b). 从文献[22]中获得274个出水SS数据,均值为12 mg ·L-1,见图 2(c); 310个二级出水BOD5数据,均值为10 mg ·L-1,见图 2(d). 一般STP的二级出水都排放进入地表水Ⅲ 类功能水域[23],因此中国的STP普遍执行“城镇污水处理厂污染物排放标准”(GB 18918-2002)[24]一级B标准(BOD5和SS都为20 mg ·L-1). 由于大部分有机化学品都会显著吸附于悬浮固体中随二级出水排出,为了符合风险评估中保守评估的原则,模型中将二级出水SS定为20 mg ·L-1.
 | 图 2 中国STP进水水质文献调研值 Fig. 2 China's water quality of STP influent by documents study |
假定STP运行良好,初沉池有2/3的污泥发生沉降,同时13/36的BOD在初沉过程中被去除,剩余23/36的BOD进入曝气池,曝气池BOD5去除率(FBOD)为90%[25]. 好氧污泥在降解BOD的过程中会生产污泥,曝气池污泥产生量(Psludge,kg ·d-1)[26]的计算见式(3).
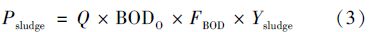
式中,Ysludge为污泥产率(kg ·kg-1); BODO为曝气池BOD5(g ·L-1); FBOD为BOD5去除率(无量纲); Ysludge为污泥产率(kg ·kg-1).
Mikkelsen等[27]研究表明Ysludge的计算见式(4).
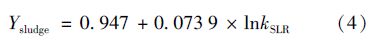
式中,kSLR为污泥负荷(kg ·kg-1),可根据FBOD计算:lnkSLR=(0.818-FBOD)/0.042 2,当曝气池FBOD=0.9时,kSLR为0.14 kg ·kg-1.
本研究选择北京、 南京、 上海、 沈阳共10家污水处理厂,采样测定了活性污泥的密度和有机碳含量. 结果显示,有机碳含量分布在18%~31%,均为20%,初沉池污泥和曝气池污泥稍有差异; 污泥密度为1.2~2 kg ·L-1,均值1.6 kg ·L-1.
模型中采用的环境条件和场景参数见表 3. 如果输入数据缺乏,可推荐使用表 3中数据.
| 表 3 C-STP(O)模型和SimpleTreat模型环境条件和场景参数 1) Table 3 Parameters of environmental conditions and scenario used in C-STP(O) model |
欧盟SimpleTreat和US EPA的STPWIN模型是国际上常用的STP暴露评估模型,STPWIN模型没有暴露场景参数的介绍,欧盟SimpleTreat模型参数比较系统,国内现阶段主要使用SimpleTreat模型预测化学品的归趋,中国与欧盟参数场景参数的差异将会对结果差生明显的差异. 中国STP进水BOD、 SS、 foc显著低于欧盟,低BOD和低SS使污泥产量较少,低foc使污泥吸附化学品量减少,最终中国场景参数使C-STP(O)模型预测的污泥对化学品的吸附比例降低,二级出水中归趋比例增加. 中国平均环境温度为283 K,略低于欧盟288 K,化学品的挥发性损失略小,对于非挥发性化学品,差异不显著. 中国STP日处理量平均值为35 000 m3 ·d-1,远高于欧盟2 000 m3 ·d-1,对于相同排放量的化学品,C-STP(O)预测的STP中的化学品浓度将是SimpleTreat预测值的1/17.
1.3 质量守恒方程及求解 1.3.1 平流(1)空气 假定STP上方空气流入速度和流出速度相同,则空气流速由风速、 污水处理厂的面积和大气高度共同决定,计算公式见式(5).
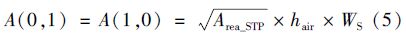
(2)水流 各池体的水流流速与污水日处理量Q成正比,计算见式(6).
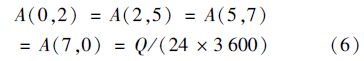
(3)悬浮颗粒流和污泥流 不同池体之间悬浮固体的流速用相应的水流速率和悬浮固体浓度计算,为了统一量纲,计算中引入污泥密度(RHO),A(0,3)、 A(6,8)、 A(8,0)计算公式相似,以A(0,3)为例,计算见式(7).
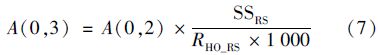
在初沉池中有2/3的悬浮颗粒沉降下来,其余1/3的悬浮颗粒进入曝气池,则A(3,6)=1/3A(0,3),A(3,4)=A(4,0)=2/3A(0,3). 进入二沉池的悬浮颗粒,一部分随二级出水流出,一部分沉降为污泥,沉降后的污泥,一部分作为剩余污泥排出,另一部分回流到曝气池,质量守恒方程分别见式(8)、 (9)和(10).
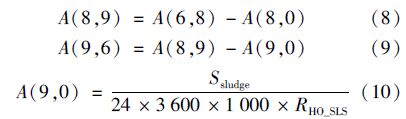
每日产生的剩余污泥量(Ssludge)为流入曝气池的污泥和曝气池污泥产生量之和减去二级出水中流出污泥量,计算公式见式(11).
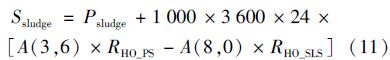
扩散过程由两个相邻的环境介质的非平衡浓度决定,STP中扩散过程包括污泥-水(吸附)和空气-水体系(挥发和曝气). Mackay创建了描述扩散过程的逸度方法[13],扩散流量X(i,j)的计算见式(12).
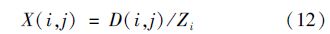
式中,D(i,j)指i箱到j箱的迁移系数[mol ·(s ·Pa)-1]; Zi为i相的逸度容量[Z,mol ·(m3 ·Pa)-1]计算.
逸度容量的概念类似于比热容,Z值高的相(可能是底泥或鱼)能吸收大量的化学品,却能保持低的逸度. 化学品在两相的迁移系数,可应用惠特曼双阻力理论,该理论假设化学品在相内迁移速度较快,迁移的限速步骤来自于迁移相和被迁移相两相的界面阻力,且总阻力为两相界面阻力之和[14]:1/D=1/D1+1/D2. 逸度理论认为[14]化学品在两相(如气-水)中的分配系数(KH)为气相逸度容量(Z1)除以水相逸度容量(Z2). 因此,与浓度模型相比,逸度模型的优点主要为计算与求解比较简单,且适用于由任意多个环境介质构成的环境系统.
(1)吸附
污泥-水分配系数(KP,L ·kg-1)为平衡状态下化学品在污泥中逸度容量(Zs)和水中逸度容量(Zw)之比[14]:
Kp=Zs/Zw
污泥的逸度容量为:
Z3=Z4=Z6=Z8=Z9=Kp×RHO/H
水的逸度容量为:
Z2=Z5=Z7=1/H
化学品在污泥中的吸附主要取决于污泥有机碳含量(foc),不同性质的污泥其化学品的Kp值不同,通常采用经foc归一化后的污泥/水吸附系数(Koc)表征化学品的吸附行为:
Koc=Kp/foc
化学品吸附过程有3种吸附模型:Langmuir模型、 Freundlich模型和线性模型,在低浓度时(即浓度<1 μg ·L-1),可使用线性模型[28]. 对于Koc无法测定的新化学物质或者缺乏数据的现有化学品,可根据Kow进行估算[29],最经典的估算方法为:
Koc=0.5×Kow
根据惠特曼双阻力公式,假定化学品在水相和悬浮颗粒相中达到了吸附平衡,污泥-水之间的D值由吸附速率(kabs,s-1)决定,
kabs=ln2/t1/2
式中t1/2为污泥吸附解析平衡一般所用的时间. 由于曝气加剧了吸附解析的速度,可以认为曝气池t1/2为360 s,初沉池和二沉池为t1/2为3 600 s. 则吸附D值[14]计算见式(13).
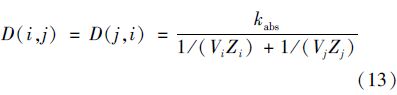
(2)挥发和曝气
纯物质的挥发性可用蒸气压或者沸点表征,但是这有别于化学品在水中的挥发过程. 水相中,平衡状态下化学品在大气中和水中的分配系数KH计算公式为[14]:
KH=P/(RTCw)
可以看出,化学物质在水气之间的分配不仅与P有关,还与S有关. 因此可以使用亨利常数(H):
H=P×M/S
表征化学物质在气水界面的分配[30]. 新化学物质申报中H为非基础数据,可根据P、 M、 S计算. 由此,空气逸度容量为:
Z1=1/(RT)
式中R为气体常数,8.314 J ·(mol ·K)-1. 水的逸度容量为:
Z2=Z5=Z7=1/H
水-气之间的迁移速率D(1,2)和D(1,7)值计算见式(14)[14].

式中,Kair为空气传质系数(2.78×10-3 m ·s-1),Kwater为水传质系数(2.78×10-5 m ·s-1). 曝气池D值计算见式(15)[31]:
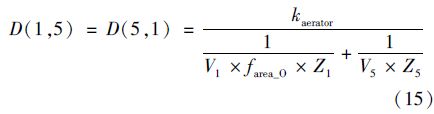
式中,kaerator为曝气池挥发速率常数,为表面挥发速率常数(ksurf)和曝气挥发速率常数(kstrip)两部分之和,
kaerator=ksurf+kstrip
这意味着化学品在曝气池中的损失大部分来自于曝气而非表面挥发. 表面挥发速率ksurf为[31]:
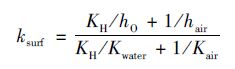
气提挥发速率常数根据Hsieh等[32]研究结果,用曝气速率计算:
kstrip=8.9×10-4(AR/3 600)/VOH1.04
1.3.3 降解化学品降解机制比较复杂,污水处理厂中低浓度化学品一般遵守一级动力学方程或Monod方程. Monod方程认为,某一微生物的比生长速率与基质(化学品)浓度相关,即化学品的降解不仅与其本身相关,还与微生物的生长过程相关,Monod方程中相关参数测定比较复杂. 目前国际上普遍认可的生物降解性测试方法为经济与合作组织(Organization for Economic Co-operation and Development,OECD)提出的生物降解性筛选试验方法,包括快速生物降解性和固有生物降解性. 快速生物降解性是一种严格的筛选试验,如果化学品在快速生物降解性中达到通过水平,则在STP中可以完全矿化. 该测试方法简单、 可靠,其结果基本可以外推到STP及环境中的降解性[33, 34].
本研究中假定化学品的降解遵守一级动力学方程,用一级动力学方程的降解速率(k)计算化学品的降解过程. 如果无法获得STP中化学品的k,可依据生物降解性筛选试验结果外推至STP中的k. OECD301、 302试验中接种物浓度为10~100 mg ·L-1范围,而STP生化反应池的悬浮固体含量为2 000~4 000 mg ·L-1,化学品在STP生化反应池的降解速率将远远高于筛选试验. 有研究认为[35],STP中生物降解速率正比于接种物中细胞数量,可以通过接种物浓度的关系计算STP中k,计算见式(16). k=k301,302× [细胞浓度]STP [细胞浓度]301,302 ×a (16) 式中,a为外推系数.
目前欧盟和美国根据快速生物降解性及固有生物降解性测试结果,制定了外推标准以获得化学品在STP中的k,分别被用于SimpleTreat和STPWIN模型. 如表 4所示. 欧盟外推标准分为4级,k分别为1、 0.3、 0.1和0 h-1,而美国外推标准分为5级,k分别为0.69、 0.23、 0.069、 0.023和6.9×10-5 h-1,分别对应DT50为1、 3、 10、 30、 10 000 h. 欧盟和美国标准降解速率基本处于相同水平,美国标准稍微严于欧盟. 根据作者研究经验及已有研究结果[35, 36],由于筛选试验条件的严格性,固有生物降解率达到20%,在污泥浓度较高的STP中一定可以发生降解,如Simonich等[37]发现水杨酸苄酯等4种具有固有生物降解性的化学品,在STP中降解去除率可以达到95.1%~99.8%. 因此欧盟将k设为0过于苛刻,美国的设置标准更为科学,本模型推荐使用美国的外推标准获取k.
| 表 4 欧盟和美国生物降解性筛选试验结果外推STP中降解速率常数的标准 [34] Table 4 Extrapolation criteria from results of biodegradation screening test to degradation rate constant in STP proposed by US EPA and EU |
STP中化学品的输入主要为原水中化学品向初沉池的流入,化学品在水和悬浮颗粒中达到吸附平衡,其中溶解态的化学品比例fdis为:
fdis=1/(1+Kp_RS×SSRS/1 000)
原水中化学品溶解态浓度c(0,2)为溶解态比例乘以原水中化学品总浓度(cin)为:
c(0,2)=cin×fdis
式中,cin根据化学品排放量和污水日处理量计算:
cin=1 000×ERC/Q
式中,ERC为化学品日排放量,kg ·d-1. 悬浮颗粒中化学品浓度c(0,3)=c(0,2)×Kp_RS.
1.4 STP暴露浓度实际采样分析酚类化学品因具有环境激素类效应、 且容易在地表水中检出[38],对生态环境具有潜在风险. 测定了5种不同归趋特性的酚类化学品在以传统活性污泥法为基本工艺的JinSh污水处理厂中的去除率. 采集上海JinSh污水处理厂原水及二级出水水样,将水样置于1 L棕色玻璃瓶内运回实验室,用盐酸调节pH值达到2±0.2,并用0.45 μm孔径玻璃纤维膜抽滤,取500 mL水样用固相萃取(Oasis HLB)小柱进行固相萃取. 先用甲醇活化固相萃取小柱,再用10 mL的去离子水淋洗HLB小柱,上样速度约为5 mL ·min-1. 上样结束后继续抽真空30 min使其干燥,用10 mL甲醇溶液洗脱,洗脱液用氮气吹干,然后用甲醇 ∶水(1 ∶1)定容到1 mL,涡旋振荡2~3 min,按照文献[39]的方法采用HPLC-MS/MS(AB Science,Qtrap4500)分析水样中苯酚类化学品浓度. 标准溶液峰面积与质量浓度的线性关系良好(R2≥0.998),方法定量限为2.0~20 ng ·L-1,添加浓度为20 μg ·L-1时,方法回收率为70.3%~102.7%.
2 模型验证及应用 2.1 文献数据验证模型Monteith[40]和Hannah等[41]研究了1,1,1-三氯乙烷等26个化学品在传统活性污泥中的去除率,本研究收集了这26个化学品的H、 lgKow以及生物降解性筛选试验数据[42],并按照US EPA的外推标准获取了在STP中的k. 26个化学品的验证数据见表 5.
| 表 5 C-STP(O)模型预测值与文献试验值比较 Table 5 Comparison of model results by C-STP(O) with the measured values reported in literature |
模型预测差异在20%为可接受范围[43],26个 化学品中预测偏差绝对值小于20%的为21个,预测准确率为81%. 预测偏差绝对值大于20%的为5个,分别为蒽(53%)、 芘(51%)、 富马酸二甲酯(35%)、 荧蒽(28%)、 溴仿(-26%). 以蒽为例,经STP处理后,分配比例分别为空气(4%)、 水(73%)、 污泥(12%)、 降解(12%),由于蒽的H=3.96 Pa ·m3 ·mol-1,挥发性不是特别强,空气中4%的分布比例也较为符合,因此预测值与实测值差异主要为污泥吸附和降解过程. 生物降解影响因素较多,受环境条件、 STP运行状况、 化学品毒性、 化学品浓度、 污泥浓度和微生物构成生物降解性差异较大,很难准确测定化学品在STP中的生物降解性.
预测偏差绝对值大于20%的5种化学品中有4种化学品,文献实测值高于本模型预测值,且这4种化学品的DT50为3~30 h,属于筛选试验中可降解但非快速生物降解类物质. 因此根据外推标准,模型采用了较低的生物降解速率,模型预测出较少的生物降解去除率. 但在实测中,这些物质可能表现出较高的生物降解速率,导致实测去除率高于本模型预测值. 由于快速生物降解试验条件的严格性,化学品未达到快速生物降解性通过水平并不能表明其在环境中不可生物降解[16]. Guhl等[44]比较了快速生物降解性和固有生物降解试验结果与污水处理厂模拟试验结果之间的符合性,发现80%的化学品结果比较一致. 其余10%~20%的化学品没有通过筛选试验,但是在模拟试验中发生降解. Painter等[45]研究结果表明由于筛选试验结果的严格性,部分筛选试验中未降解性的化学品在STP中的降解率亦可达到90%以上. 因此可以认为,上述4种化学品预测结果的差异是因为筛选试验外推得到的降解速率未能充分反映其在STP中的降解性,这种差异是因为模型输入参数k的不确定性引起,非模型预测结果原因,如果输入参数准确,如使用试验测定的活性污泥中生物降解速率常数,则模型本身预测结果应更能符合实际情况.
2.2 实测数据验证模型JinSh污水处理厂工艺为传统活性污泥法,5种酚类化学品去除率结果见表 6. 5种酚类化学品去除率为37.9%~98.5%,C-STP(O)预测去除率为44%~96%,SimpleTreat模型预测去除率为78%~90%,C-STP(O)模型预测值与实测值绝对差值为2.5%~6.3%,SimpleTreat模型预测值与实测值绝对差值为0.2%~43%. 由于C-STP(O)模型中BOD、 SS、 foc等参数小于SimpleTreat模型,对于5种中等吸附性的酚类化学品(lgKoc为3.17~4.54),C-STP(O)模型预测的的污泥吸附比例相对于SimpleTreat模型偏小.
| 表 6 5种苯酚类化学品在STP中去除率实测值和预测值比较 Table 6 Removal comparison of model results with experimental values for 5 phenols |
对特辛基苯酚实测值、 C-STP(O)预测值、 SimpleTreat预测值分别为37.9%、 44%、 81%,相比SimpleTreat模型,C-STP(O)预测结果差异较大. 一方面,是因为C-STP(O)在吸附性参数上更符合中国实际情况,另一方面,对特辛基苯酚28 d生物降解率>60%,10 d观察期降解率<60%,SimpleTreat模型k=0.3 s-1,而C-STP(O)模型采用的k=0.23 s-1,说明C-STP(O)的k取值为标准也较为合理.
2-甲基-5-异丙基苯酚在JinSH STP进水中检出浓度最高,为2 670 ng ·L-1,2,4-二叔戊基苯酚检出浓度最低,为34.0 ng ·L-1,虽然不同化学品暴露浓度水平差异较大,但是C-STP(O)模型预测结果与实测值都较为一致.
化学品在污水处理厂中除了能够发生吸附、 挥发、 生物降解外,还可能发生水解和光解,这也会导致模型预测结果与实测结果产生差异. 鉴于大多数化学品具有较小的水解和光解速率,且在新化学物质申报中,光解速率非基础数据,因此C-STP未考虑水解和光解的影响.
2.3 化学品在C-STP(O)中分布规律为了研究不同吸附性、 挥发性化学品在C-STP(O)中的归趋. 将化学品降解性设置为0(持久性有机化学品),然后通过输入不同的lgKow和H,分析C-STP(O)模型向水、 大气、 污泥的排放比例预测值,结果见图 3.
 | H为亨利常数(Pa ·m3 ·mol-1)图 3 C-STP(O)模型中lgKow和H对化学品分配比例的影响 Fig. 3 Influence of lgKow and H on distribution of chemicals in C-STP(O) model |
当疏水性增加时,即lgKow从-1增加到10,排放到水中化学品比例逐渐减少,排放到污泥的比例相应增加. 在lgKow为3~9范围内,排放到水中的化学品比例迅速减少,排放到污泥的比例迅速增加. 表明,随着lgKow增加,化学品主要去除过程为污泥吸附,导致向水体和大气的排放比例降低. McCall等[46]研究了化学品在土壤中的迁移能力,同时按照lgKoc值对化学品在土壤中的迁移能力进行了分级,当lgKoc>3.3(lgKow>3)时,化学品在土壤中具有极低的移动能力,较好的符合C-STP(O)的预测结果.
C-STP(O)预测结果显示,在无污泥吸附时(lgKow为1~3),当H从1 Pa ·m3 ·mol-1增加到100 Pa ·m3 ·mol-1,化学品排放到水中的比例大量减少,排放到空气中比例的增加,化学品倾向于挥发进行大气. 根据Whiteman双阻力理论,当H=25 Pa ·m3 ·mol-1时,化学品在液相和气相中的迁移阻力相等,H>25 Pa ·m3 ·mol-1时,化学品在气相中的迁移阻力低于液相,挥发限速步骤为水相的迁移速率. 当H=2.5 Pa ·m3 ·mol-1时,水相的阻力为气相阻力的十分之一,气相迁移速率可以忽略. 由于化学品在空气中的迁移阻力较小,因此,非挥发性化学品的迁移阻力都来源于气相,使得化学品不容易从水中挥发到空气中. 水的H=0.04 Pa ·m3 ·mol-1,当化学品H低于该值时,化学品的挥发速率低于水的挥发速率,在水的蒸发过程中,化学品会在水中浓缩,化学品成为真正的非挥发性化学品[14].
而在H变化的过程中吸附到污泥中的比例变化不明显,分布曲线几乎重叠在一起,表明亨利常数的改变几乎不影响污泥对化学品的吸附量.
2.4 3种化学品的归趋行为预测选择3种不同性质的化学品:1,1,2-三氯乙烷(易挥发)、 萘(易降解)、 邻苯二甲酸(2-乙基己基)酯(DEHP)(易吸附),用所建C-STP(O)模型预测在STP中的归趋,结果见图 4.
 | (a)1,1,2-三氯乙烷; (b)萘; (c)邻苯二甲酸(2-乙基己基)酯 图 4 C-STP(O)模型中不同特性化学品的归趋 Fig. 4 Detailed fate and distribution of chemicals with different properties in C-STP(O) model |
1,1,2-三氯乙烷lgKow=2.53,吸附性较小(lgKow<3),可以看出原水中化学品在水相中的比例为99.2%,在悬浮固体中的比例为0.77%. H=1 183 Pa ·m3 ·mol-1,挥发性极大,在初沉池、 曝气池、 二沉池挥发比例分别为4.52%、 63.4%和3.40%,曝气过程中此类化学品的挥发比例非常大. 该物质挥发进入大气后,很难降解,且会消耗臭氧层,已在全球范围内限制使用.
萘的lgKow=3.37,原水中化学品在悬浮固体中的比例为2.09%,呈现一定的吸附作用. 萘的H=43 Pa ·m3 ·mol-1,属于易挥发物质,因此初沉池挥发比例为2.09%,但是由于萘的降解性非常好(DT50=1 h),因此,其在曝气池中主要发生降解,挥发比例只有2.3%. 北京6家STP污泥中萘的检出含量[47]为0.01~0.18 mg ·kg-1,该值也表明,由于降解的原因,污泥不是萘主要的归趋介质.
DEHP的H=1.73 Pa ·m3 ·mol-1,挥发性较小,lgKow=7.5,吸附性极强,从图 3中看出原水中化学品在悬浮固体中的吸附比例高达75%,因此在初沉池沉降污泥的去除率就达到50.0%,总的污泥去除率为64%. 此类吸附性化学品从二级出水排放进入地表水中后,会吸附进入水体沉积物中,如2000年在太湖12个点采集的沉积物样品中[48],DEHP检出含量为2.22~23.93 mg ·kg-1. 长江武汉段干流[49]中DEHP浓度为0.011~54.7 μg ·L-1,沉积物中含量为0.4~323 mg ·kg-1,黄河干流[50]中DEHP浓度为0.34~24 mg ·L-1,沉积物中含量为9.3~51 mg ·kg-1,都呈现从水相向沉积物转移的较强趋势,由于疏水性极强,微生物很难利用,在环境中的降解速率较慢.
3 结论(1)调研了我国STP的典型场景参数,温度=283 K、 风速=2 m ·s-1、 日处理量=3.5万m3 ·d-1、 进水BOD5=0.15 g ·L-1、 进水SS=0.2 kg ·m-3、 出水SS(dw)=0.02 kg ·m-3、 曝气池BOD5去除率=90%、 污泥密度(dw)=1.6 kg ·L-3、 污泥有机碳含量为0.18~0.19.
(2)以STP中最简单的传统活性污泥法为基础工艺,根据化学品的挥发、 吸附、 降解特性,依据质量守恒和逸度理论,将环境介质划分为9箱,建立了STP暴露预测模型C-STP(O).
(3)模型仅需输入亨利常数、 生物降解速率常数、 吸附系数即可实现化学品归趋和暴露预测. 模型还使用了亨利常数、 吸附系数的估算方法以及生物降解性的外推方法.
(4)模型验证结果表明,C-STP(O)能准确预测化学品在STP中挥发、 吸附、 降解、 二级出水的分配过程和分布比例,模型预测结果的不确定性主要为生物降解速率常数.
| [1] | van Leeuwen D J, Vermeire T G. Risk assessment of chemicals: an introduction[M]. (2nd ed.). Netherlands: Springer, 2007. 1-16. |
| [2] | Martin R S, Choubert J M, Budzinski H, et al. Occurrence and fate of relevant substances in wastewater treatment plants regarding Water Framework Directive and future legislations[J]. Water Science and Technology, 2012, 65 (7): 1179-1189. |
| [3] | 陈春丽, 王铁宇, 吕永龙, 等. 河流及污水处理厂全氟化合物排放估算[J]. 环境科学, 2011, 32 (4): 1073-1080. |
| [4] | Choubert J M, Ruel S M, Esperanza M, et al. Limiting the emissions of micro-pollutants: what efficiency can we expect from wastewater treatment plants?[J]. Water Science and Technology, 2011, 63 (1): 57-65. |
| [5] | 温智皓, 段艳平, 孟祥周, 等. 城市污水处理厂及其受纳水体中5种典型PPCPs的赋存特征和生态风险[J]. 环境科学, 2013, 34 (3): 927-932. |
| [6] | Gujer W, Henze M, Mino T, et al. Activated sludge model No. 3[J]. Water Science and Technology, 1999, 39 (1): 183-193. |
| [7] | Urase T, Kikuta T. Separate estimation of adsorption and degradation of pharmaceutical substances and estrogens in the activated sludge process[J]. Water Research, 2005, 39 (7): 1289-1300. |
| [8] | Plósz B G, Leknes H, Thomas K V. Impacts of competitive inhibition, parent compound formation and partitioning behavior on the removal of antibiotics in municipal wastewater treatment[J]. Environmental Science & Technology, 2010, 44 (2): 734-742. |
| [9] | Franco A, Struijs J, Gouin T, et al. Evolution of the sewage treatment plant model simple treat: use of realistic biodegradability tests in probabilistic model simulations[J]. Integrated Environmental Assessment and Management, 2013, 9 (4): 569-579. |
| [10] | Clark B, Henry G L H, Mackay D. Fugacity analysis and model of organic chemical fate in a sewage treatment plant[J]. Environmental Science & Technology, 1995, 29 (6): 1488-1494. |
| [11] | Seth R, Webster E, Mackay D. Continued development of a mass balance model of chemical fate in a sewage treatment plant[J]. Water Research, 2008, 42 (3): 595-604. |
| [12] | Byrns G. The fate of xenobiotic organic compounds in wastewater treatment plants[J]. Water Research, 2001, 35 (10): 2523-2533. |
| [13] | Mackay D. Multimedia Environmental Models: The Fugacity Approach[M]. Boca Raton, FL: Lewis Publishers, 1991. 257-258. |
| [14] | Mackay D著,黄国兰译. 环境多介质模型:逸度方法[M]. 北京: 化学工业出版社, 2007. 108-110. |
| [15] | 刘纯新. 化学品测试方法——理化特性和物理危险性卷[M]. (第二版). 北京: 中国环境科学出版社, 2013. |
| [16] | 刘纯新. 化学品测试方法——降解与蓄积卷[M]. (第二版). 北京: 中国环境科学出版社, 2013. |
| [17] | 中国气象局. 2014年中国气候公报[EB/OL]. http://www.cma.gov.cn/2011zwxx/2011zxxgk/zxgk/201501/P020150129395699895064.pdf" target=_blank title="点击浏览原文">http://www.cma.gov.cn/2011zwxx/2011zxxgk/zxgk/201501/P020150129395699895064.pdf" target=_blank title="点击浏览原文">http://www.cma.gov.cn/2011zwxx/2011zxxgk/zxgk/201501/P020150129395699895064.pdf, 2015-01-12/2015-01-30. |
| [18] | 傅献彩. 物理化学[M]. (第五版). 北京: 高等教育出版社, 2006. 277-278. |
| [19] | 中国环境保护部. 关于公布2014年全国投运城镇污水处理设施名单的公告[EB/OL]. http://www.zhb.gov.cn/gkml/hbb/bgg/201506/t20150609_303209.htm" target=_blank title="点击浏览原文">http://www.zhb.gov.cn/gkml/hbb/bgg/201506/t20150609_303209.htm" target=_blank title="点击浏览原文">http://www.zhb.gov.cn/gkml/hbb/bgg/201506/t20150609_303209.htm, 2015-05-26/2015-08-05. |
| [20] | GB 50014-2006, 室外排水设计规范(2014年版)[S]. |
| [21] | 胡春萍. 广州市大坦沙污水处理厂(三期)工程设计研究[D]. 天津: 天津大学, 2004. 10-23. |
| [22] | 陈贻龙. 广州市沥窖污水处理厂一期工程的设计及运行[J]. 中国给水排水, 2010, 26 (12): 70-73. |
| [23] | GB 3838-2002, 地表水环境质量标准[S]. |
| [24] | GB 18918-2002, 城镇污水处理厂污染物排放标准[S]. |
| [25] | 邵林广. 城市污水处理中初沉池的设置[J]. 给水排水, 2001, 27 (9): 5-7. |
| [26] | Deng Q, Tanner R D. Modeling the dynamics of an activated sludge process using yield and growth functions[J]. Journal of Chemical Engineering of Japan, 2006, 39 (8): 846-854. |
| [27] | Mikkelsen J, Nyholm N, Jacobsen B N, et al. Evaluation and modification of the simpletreat chemical fate model for activated sludge sewage treatment plants[J]. Water Science and Technology, 1996, 33 (6): 279-287. |
| [28] | Limousin G, Gaudet J P, Charlet L, et al. Sorption isotherms: a review on physical bases, modeling and measurement[J]. Applied Geochemistry, 2007, 22 (2): 249-275. |
| [29] | Jacobsen B N, Nyholm N, Pedersen B M, et al. Removal of organic micropollutants in laboratory activated sludge reactors under various operating conditions: sorption[J]. Water Research, 1993, 27 (10): 1505-1510. |
| [30] | Mackay D, Shiu W Y. A critical review of henry's law constants for chemicals of environmental interest[J]. Journal of Physical and Chemical Reference Data, 1981, 10 (4): 1175-1199. |
| [31] | Struijs J. Simple Treat 3.0: a model to predict the distribution and elimination of chemicals by sewage treatment plants[R]. Netherland: RIVM Report, 1996. 5-15. |
| [32] | Hsieh C C, Babcock R W, Stenstrom M K. Estimating emissions of 20 VOCs. II: Diffused aeration[J]. Journal of Environmental Engineering, 1993, 119 (6): 1099-1118. |
| [33] | Federle T W, Gasior S D, Nuck B A. Extrapolating mineralization rates from the ready CO2 screening test to activated sludge, river water and soil[J]. Environmental Toxicology and Chemistry, 1997, 16 (2): 127-134. |
| [34] | Boethling R S, Howard P H, Beauman J A, etal. Factors for intermedia extrapolation in biodegradability assessment[J]. Chemsphere, 1995, 30 (4): 741-752. |
| [35] | Struijs J, van den Berg R. Standardized biodegradability tests: extrapolation to aerobic environments[J]. Water Research, 1995, 29 (1): 255-262. |
| [36] | Gotvajn A Z, Zagorc-Koncan J. Comparison of biodegradability assessment tests for chemical substances in water[J]. Water Science and Technology, 1996, 33 (6): 207-212. |
| [37] | Simonich S L, Federle T W, Eckhoff W S, et al. Removal of fragrance materials during U.S. and European wastewater treatment[J]. Environmental Science & Technology, 2002, 36 (13): 2839-2847. |
| [38] | 吴正勇, 赵高峰, 周怀东, 等. 三峡库区丰水期表层水中酚类的分布特征及潜在风险[J]. 环境科学, 2012, 33 (8): 2580-2585. |
| [39] | 丁洁, 张圣虎, 刘济宁, 等. 液相色谱-串联质谱法测定污水处理厂水样中双酚A、四溴双酚A及烷基酚类化合物[J]. 色谱, 2014, 32 (5): 529-534. |
| [40] | Monteith H. Fluctuations of Trace Contaminants in Sewage Treatment Plants, Monograph Series 1 on Advances in Water Pollution Research &Technology[M]. Burlington, Ontario: Canadian Association on Water Pollution Research & Control, 1987. 186-193. |
| [41] | Hannah S A, Austern B M, Eralp A E, et al. Comparative removal of toxic pollutants by six wastewater treatment processes[J]. Water Pollution Control Federation, 1986, 58 (1): 27-34. |
| [42] | Mackay D, Shiu W Y, Ma K C. Illustrated handbook of physical-chemical properties and environmental fate for organic chemicals[M]. Boca Raton, FL: CRC Press, 1992. 195. |
| [43] | Katsoyiannis A, Zouboulis A, Samara C. Persistent organic pollutants (POPs) in the conventional activated sludge treatment process: Model predictions against experimental values[J]. Chemosphere, 2006, 65 (9): 1634-1641. |
| [44] | Guhl W, Steber J. The value of biodegradation screening test results for predicting the elimination of chemicals' organic carbon in waste water treatment plants[J]. Chemosphere, 2006, 63 (1): 9-16. |
| [45] | Painter H A, King E F. A mathematical model of biodegradability screening tests as an aid to interpretation of observed results[J]. Regulatory Toxicology and Pharmacology, 1983, 3 (2): 144-151. |
| [46] | McCall P J, Swann R L, Laskowski D A, et al. Estimation of chemical mobility in soil from liquid chromatographic retention times[J]. Bulletin Environmental Contamination and Toxicology, 1980, 24 (1): 190-195. |
| [47] | Dai J Y, Xu M Q, Chen J P, et al. PCDD/F, PAH and heavy metals in the sewage sludge from six wastewater treatment plants in Beijing, China[J]. Chemosphere, 2007, 66 (2): 353-361. |
| [48] | Wang H, Wang C X, Wu W Z, et al. Persistent organic pollutants in water and surface sediments of Taihu Lake, China and risk assessment[J]. Chemosphere, 2003, 50 (4): 557-562. |
| [49] | 王凡, 沙玉娟, 夏星辉, 等. 长江武汉段水体邻苯二甲酸酯分布特征研究[J]. 环境科学, 2008, 29 (5): 1163-1169. |
| [50] | 沙玉娟, 夏星辉, 肖翔群. 黄河中下游水体中邻苯二甲酸酯的分布特征[J]. 中国环境科学, 2006, 26 (1): 120-124. |
 2016, Vol. 37
2016, Vol. 37


