环境科学  2014, Vol. 35 Issue (9): 3389-3396   PDF    
引用本文
李渊, 李云梅, 吕恒, 朱利, 吴传庆, 杜成功, 王帅. 基于数据同化的太湖叶绿素多模型协同反演[J]. 环境科学, 2014, 35(9): 3389-3396.
LI Yuan, LI Yun-mei, LÜ Heng, ZHU Li, WU Chuan-qing, DU Cheng-gong, WANG Shuai. Muti-model Collaborative Retrieval of Chlorophyll a in Taihu Lake Based on Data Assimilation[J]. Environmental Science, 2014, 35(9): 3389-3396.
基于数据同化的太湖叶绿素多模型协同反演
李渊1, 李云梅1 , 吕恒1, 朱利2, 吴传庆2, 杜成功1, 王帅1    
1. 南京师范大学虚拟地理环境教育部重点实验室, 南京 210023;
2. 环境保护部卫星环境应用中心, 北京 100029
收稿日期: 2014-2-28; 修订日期: 2014-4-16.
基金项目： 国家自然科学基金项目（41271343）；高分辨率对地观测系统重大专项（05-Y30B02-9001-13/15-6）；江苏高校优势学科建设工程项目；中国科学院数字地球重点实验室开放基金项目（2012LDE009）
作者简介：李渊（1985~），男，博士研究生，主要研究方向为数据同化、环境遥感监测，E-mail：liyuannjnu@163.com
通讯联系人,李云梅,E-mail: yunmei2009@gmail.com
摘要：在国内外众多学者的不懈努力下，开发了大量的水质参数遥感估算反演模型，但不同的模型都具有其“局限性”，只能从某个层面反映“真值”. 基于上述考虑，本研究发展了基于数据同化方法的太湖叶绿素a浓度多模型协同反演算法. 利用2006~2009年太湖野外实测水体高光谱遥感反射率数据，构建了7个叶绿素a浓度反演模型；通过模型精度对比，最终遴选出6个适宜的叶绿素a浓度反演模型. 进而使用不同模型组合，进行多模型协同反演. 结果表明：1多模型协同反演算法的反演精度要高于单模型反演的反演精度，最优MAPE仅为22.4%；2随着参与多模型协同反演的模型个数的增加，其反演精度也逐渐提高，MAPE均值从25.6%降低到23.4%，RMSE均值从15.082 μg ·L-1降低到14.575 μg ·L-1，相关系数R均值从0.91提升到0.92；3通过对多模型协同反演产品的置信区间进行计算，可以有效地估算产品精度和误差，同时使得获取全湖反演叶绿素a浓度的误差空间分布情况成为可能.
关键词： 高光谱数据     叶绿素     数据同化     太湖     多模型协同反演    
Muti-model Collaborative Retrieval of Chlorophyll a in Taihu Lake Based on Data Assimilation
LI Yuan1, LI Yun-mei1 , LÜ Heng1, ZHU Li2, WU Chuan-qing2, DU Cheng-gong1, WANG Shuai1    
1. Key Laboratory of Virtual Geographic Environment, Ministry of Education, Nanjing Normal University, Nanjing 210023, China;
2. Satellite Environment Application Center, Ministry of Environmental Protection, Beijing 100029, China
Abstract: Under the efforts of many scholars, large amount of remote retrieval models of water quality parameters have been developed. However, each model could only reflect the "true value" from one level because of the natural limitation of remote sensing. To get the relatively true value by combining various retrieval models, in this work, we developed a multi-model collaborative retrieval algorithm for retrieving the concentration of Chlorophyll a based on data assimilation. We measured water quality parameters and water reflectance spectra in Taihu Lake during 2006 to 2009. There were seven retrieve models established and six models were selected to participate in the multi-model collaborative retrieval algorithm. Then these selected models were combined to establish a multi-model for retrieving the concentration of Chlorophyll a. The results indicated: 1 the accuracy of multi-model retrieval algorithm was better than that of single-model retrieval method, with an optimal MAPE of only 22.4%; 2 with more models participating in the multi-model collaborative retrieval algorithm, the accuracy became better, the average MAPE was decreased from 25.6% to 23.4%, the average RMSE was decreased from 15.082 μg ·L-1 to 14.575 μg ·L-1, and the average correlation coefficient was improved from 0.91 to 0.92; 3 the accuracy and errors of retrieval products could be effective evaluated through calculating the confidence interval, which makes possible the acquirement of spatial and temporal error distribution of Chlorophyll a concentration retrieval in Taihu Lake.
Key words: hyperspectral data     chlorophyll a     data assimilation     Taihu Lake     multi-model collaborative retrieval algorithm    

叶绿素a作为浮游藻类的主要色素组成之一，是衡量水体浮游植物生物量和水体富营养化的重要参数之一，同时也是反映水体初级生产力和参与水气界面碳循环的重要参数之一. 相对于大洋水体而言，内陆湖泊的水色要素组成更为复杂，利用遥感手段和方法反演内陆湖泊叶绿素a浓度面临更大的不确定性[1]，目前还无法找到一个普适性强、 精度高的反演模型[2]. 目前所建立的大量的经验模型、 半经验模型以及分析模型，其模型的精度随着研究区域、 时间、 季节的变化而不同[3, 4, 5, 6]. 即使是同一研究区的水体，其水体光学特性也可能存在差异，导致其不同区域需要采用不同的模型[7,8]. 正因为如此，内陆水体叶绿素浓度的遥感反演面临两大困惑，一方面，各种模型不断涌现，导致在实际应用中无所适从，难以选择； 另一方面，各类模型都有其局限性，都只能从某个层面反映“真值”. 因此，联合利用前人的研究成果，通过对多个模型的综合反演，使得遥感反演更加逼近真值，是提高水环境遥感监测模型精度和适用性的重要手段.

数据同化是根据一定的数学模式和优化标准，在考虑不同数据源的误差信息基础上，将不同空间、 不同时间、 采用不同手段获得的观测资料有机结合，进而得到一个更加逼近客观现实的“真值”. 数据同化方法提供了将多模型、 多数据融合的可能性，利用数据同化方法可以融合和吸收不同模型、 数据的优势，克服和避免不同模型、 数据的不足之处，从而达到最优的反演效果. 目前，数据同化技术已经广泛应用于气象、 土壤、 水文、 海洋、 生态等多个领域[9, 10, 11]. 黄春林等[12]基于集合卡尔曼滤波的方法，采用集合卡尔曼滤波和简单生物圈模型(SiB2)的单点陆面数据同化方案，显著地提高了表层、 根区、 深层土壤水分的估算精度. 赵骞等[13]利用NASA高分辨率的卫星遥感资料SST，采用Nudging同化来模拟渤海、 黄海、 东海的三维温度场，减小用热通量作上边界条件所带来的误差. 数据同化后的温度场优于未经同化的温度场. Losa等[14]利用CZCS影像数据，采用变分法在北大西洋进行了模拟实验. 结果显示，叶绿素浓度的空间分布特性得到了有效的改善. 但在沿海和部分高纬度区域，受到数据质量的影响，同化结果受到了影响.

本研究利用相对成熟的叶绿素a浓度遥感估算模型，构建叶绿素a浓度反演模型集，提出基于数据同化方法的太湖叶绿素a浓度多模型协同反演算法，通过利用数据同化方法融合多模型反演结果，以期达到提高叶绿素a浓度反演精度的目的. 1 材料与方法 1.1 研究区与样点分布

太湖是我国第三大淡水湖，是长江中下游地区最典型的浅水型湖泊，全湖水面面积2338 km2，湖泊长度69 km，平均宽度34 km，平均水深1.89 m，平底水浅是太湖湖盆的一个显著特点[15]. 2006~2009年共4次太湖野外实验，其样点分布如图 1所示，对叶绿素a浓度及相应样点的实测高光谱遥感反射率数据等进行了测量.

图 1 太湖采样点分布示意Fig. 1 Distribution of sample stations in Taihu Lake
1.2 参数的测定

叶绿素浓度的测量采用常规的化学分析方法，用0.45 μm的GF/F滤膜过滤，90%的热乙醇提取，然后利用分光光度计检测，叶绿素浓度获取的详细步骤见文献[16]. 水体的高光谱遥感反射率数据是采用美国ASD公司生产的ASD FieldSpec Pro 便携式光谱辐射计测量，该仪器的波段范围为350~1050 nm，光谱分辨率为3 nm. 水体高光谱遥感反射率测量方法及详细步骤见文献[17]. 1.3 叶绿素浓度反演模型的遴选和重构

通过对比文献中模型方法，遵循模型易于构建、 易于业务化运行的原则，认为波段组合方法、 三波段方法和四波段方法是构建叶绿素a浓度反演模型的较适宜的模式，因此，利用在太湖实验获取的观测数据，以上述3种模式构建叶绿素浓度反演模型集.

波段组合方法结合叶绿素a光谱特征，考虑不同波段组合与叶绿素a浓度的相关性，选取相关性最高的波段组合作为叶绿素a浓度的反演因子. 进而采用相关的统计回归方法，构建叶绿素a浓度反演模型. 该类方法目前使用得比较多的是红光与近红外波段比值，例如Yacobi等[18]在以色列的Kinneret湖，利用红光和近红外波段处的光谱构建叶绿素a浓度的波段比值模型，并取得了较好的效果. Gurlin等[19]针对浑浊水体探讨了利用近红外区域的波段构建波段比值模型反演叶绿素a浓度的适用性，认为发展统一的近红外区域的波段比值模型具有很大的发展潜力.

三波段方法首先由DallOlmo等[20]于2003年提出，该方法基于水体辐射传输原理，通过率定特定波段范围的3个波段，简化了模型的形式和输入参数，大大提高了模型的实用性，该方法已被大量文献引用. 在不同的研究中，3个波长的具体位置往往会发生一些小的变化，例如Gitelson等[21]在对浑浊富营养化的Chesapeake海湾水体中的叶绿素a浓度进行遥感反演时，选择λ1、 λ2和λ3的最佳位置分别为675、 695和730 nm； 而在对Nebraska和Lowa境内的多个湖泊和水库水体进行研究后，认为λ1、 λ2和λ3三波段的最佳范围分别为660~670、 700~730和740~760 nm[22].

四波段方法2009年由Le等[23]提出. 该方法针对内陆浑浊水体中悬浮颗粒物的后向散射和吸收不可忽略的特点，在三波段模型中增加了第四波段以消减后向散射的影响，提高了模型对内陆浑浊水体的适用性，该方法已在多个区域的研究中得到应用，例如周琳等[24]利用四波段方法在巢湖进行了叶绿素a浓度的反演，并取得了较好的效果，实验结果证明四波段方法适用于内陆高浑浊水体的叶绿素a浓度反演. 1.4 基于数据同化的多模型协同反演算法

经典的数据同化理论由模型算子、 观测算子、 误差估计算子和最优化算法组成. 其目标函数是在考虑背景误差与观测误差的情况下，通过最优化算法产生一个最优分析值，使之能够更加准确地表达和描述真实状态变量. 该目标函数的表达式为：

式中，J是目标函数； H是观测算子，其作用是将状态变量转为观测变量； yo是观测值； R是观测误差协方差矩阵； B是背景场误差协方差矩阵； xb是背景值； xa是分析值. 数据同化的目标就是通过最小化目标函数J，产生最优分析值xa. 本研究中，基于上述思想发展了多模型协同反演算法. 其目标函数表达式为：

式中，J是目标函数； n为模型个数； xi为不同模型的反演值； Ri为不同模型的模型误差； xa为分析值. 通过对式(2)求梯度并令其等于0，可以求得最优分析值xa. 其表达式为：

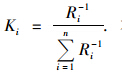其中. 本研究中，使用均方根误差(RMSE)来描述模型的模型误差.

通过对模型反演结果的对比分析，发现同一模型对不同水体区域、 不同浓度等级的叶绿素反演精度不尽相同. 因此，为了避免使用统一的权值对模型的不确定性表达失真的情况，将叶绿素a按照浓度进行等级分类，将每类的RMSE作为该模型在此浓度等级上的模型误差. 利用该方法求得的最优分析值xa是对多模型反演值的加权平均.

综上，多模型协同反演算法的计算流程如下：首先，构建叶绿素a浓度反演的模型集； 其次，对建模数据进行浓度等级划分，逐一评估每个反演模型在相应浓度等级上的模型误差. 进行参数反演时，首先根据模型集分别估算每个样点的叶绿素浓度，然后查找对应的模型误差； 最后，利用式(3)计算最优分析值，便可以得到叶绿素a浓度的最优估计. 具体流程见图 2.

图 2 多模型协同反演算法流程示意Fig. 2 Flow chart of multi-model retrieval algorithm
1.5 模型精度评价

均方根误差(RMSE)、 平均绝对误差(MAPE)、 偏差(bias)和Nash-Sutcliffe系数(Nr)被用来衡量和刻画模型的精度. 其计算公式分别为：

式中，ximod为模型估算值，ximea为测量值， mea为测量数据的均值，n为样本个数. 其中Nash-Sutcliffe系数是通过对比模型估算值与测量值的均值来评价模型好坏的重要参数之一，当Nash-Sutcliffe系数愈接近于1，说明模型愈精确； 当Nash-Sutcliffe系数愈接近于0，说明模型估算值愈接近于测量的均值； 当Nash-Sutcliffe系数小于0，说明模型效果不如使用测量值的均值，即模型不准确. 2 结果与讨论 2.1 叶绿素a浓度反演模型集

2006~2009年共进行了4次太湖野外实验，由于有部分样点的光谱表现出绿色植被的光谱特征或受到云等因素的影响，须予以剔除. 去除光谱异常数据后剩余108个样点数据. 随机选取83个数据用来构建叶绿素a浓度反演模型，25个数据用来模型验证. 按照1.3节中提及的半分析方法，结合本次野外数据，分别构建波段比值模型、 三波段模型和四波段模型.

同时，为了寻求最佳的叶绿素a浓度反演模型，本研究中还考虑了几种常用的经典模型，以三波段为代表. DallOlmo等[25]提出利用[R-1rs(671)-R-1rs(710)]Rrs(740)因子构建估算模型； Gitelson等[21]提出利用[R-1rs(675)-R-1rs(695)]Rrs(730)因子构建估算模型； 周冠华等[26]提出利用[R-1rs(666)-R-1rs(688)]Rrs(725)因子构建估算模型； 徐京萍等[27]提出利用[R-1rs(690)-R-1rs(693)]Rrs(799)因子构建估算模型. 这4个常用模型是利用本期实测数据重新建模得到模型参数，并非原始参数.

最终，针对本期野外实测数据，本研究共建立了7个叶绿素a浓度反演模型(表 1). 从表 1中可以看出，三波段模型与四波段模型的决定系数最高，分别达到了0.94. 而4个经典常用模型的决定系数较低，并且随着研究区的不同、 样本数据的不同波段位置也不同. 由此可见，无论波段比值模型、 三波段模型还是四波段模型其普适性较低. 针对这7个模型的验证，反演统计结果见表 2. 从中可以看出，DallOlmo模型和徐京萍模型的反演效果最好，MAPE仅为25%，其次是Gitelson模型和波段比值模型，MAPE为27%和29%. 对于4个经典常用模型而言，周冠华模型的精度最低，MAPE高达66%，说明该模型不太适用于太湖叶绿素a浓度反演. 因此，该模型将不参与后面的多模型协同反演. 不同的反演模型针对同一浓度等级的叶绿素a反演结果也是不尽相同(分析见2.2节)，有的模型针对低浓度区的估算结果较好，有的模型针对高浓度区的估算结果较好.

表 1 叶绿素a反演模型Table 1 Chlorophyll a retrieval model calibration

表 2 叶绿素a反演模型验证Table 2 Chlorophyll a retrieval model validation
2.2 叶绿素a浓度多模型协同反演验证

本次野外实验一共获得108个有效叶绿素a浓度数据，其中最小值为3.15 μg ·L-1，最大值为226.66 μg ·L-1. 为了避免使用统一的权值对模型的不确定性表达失真的情况，笔者将叶绿素a按照浓度进行等级分类，计算每个浓度等级上的RMSE，进而将此RMSE作为该模型在此浓度等级上的模型误差. 将本次建模数据83个样点分为11组，浓度等级分别为0~10、 10~20、 20~30、 30~40、 40~50、 50~60、 60~70、 70~80、 80~90、 90~100 μg ·L-1和>100 μg ·L-1. 进而，针对每组样点数据，进行RMSE统计计算(图 3)，以此作为模型在该浓度等级上的模型误差. 从图 3中可以看出，不同的模型在同一浓度等级上的误差不尽相同，而同一模型在不同浓度等级上的反演误差也是不同的. 例如：四波段模型在浓度等级>100 μg ·L-1上的反演RMSE高达79.29 μg ·L-1，而在浓度等级为70~80 μg ·L-1上的反演RMSE却为5.53 μg ·L-1； 在浓度等级20~30 μg ·L-1上，参与数据同化的6个反演模型的RMSE分别为9.95、 11.43、 7.62、 14.41、 11.01、 9.47 μg ·L-1.

图 3 不同反演模型的模型误差Fig. 3 Distribution of model error for different retrieval model at the same chla concentration level

由于周冠华模型不参与多模型协同反演，至此，本研究就获得了6个模型在各个浓度等级上的模型误差. 进而，针对验证点数据，依据每个模型对叶绿素a浓度的反演值就可获得不同模型对该点的模型误差. 最后，分别使用2模型组合(从6个反演模型中任意选取2个模型进行多模型协同反演，共计15个组合)、 3模型组合(从6个反演模型中任意选取3个模型进行多模型协同反演，共计20个组合)、 4模型组合(从6个反演模型中任意选取4个模型进行多模型协同反演，共计15个组合)、 5模型组合(从6个反演模型中任意选取5个模型进行多模型协同反演，共计6个组合)、 6模型组合(从6个反演模型中任意选取6个模型进行多模型协同反演，共计1个组合)协同反演叶绿素a浓度，其统计分析结果见表 3. 从表 3中可以看出，多模型协同反演的效果优于使用单模型反演，各项统计参数也较单模型反演有所提升. 其中，最优MAPE仅为22.4%，低于使用单模型反演时的最优模型——DallOlmo模型； 相关系数的均值也达到了0.913，说明反演值和真值之间具有很好拟合精度，同时也说明多模型协同反演算法具有很高的预测精度. 随着模型个数的增加，多模型协同反演算法的精度也逐渐提升. MAPE均值从2模型的25.6%降低到6模型的23.4%，RMSE均值也从2模型的15.082 μg ·L-1降低到7模型的14.575 μg ·L-1，相关系数R均值从0.91提升到0.92； 由6个模型参与的多模型协同反演结果，验证精度较单模型1~6相比，相关系数、 平均绝对误差、 均方根误差这3个指标均有所提高. 由此可见，随着参与多模型协同反演的模型个数的增加，反演结果的精度也越高. 即随着模型个数的增加，丰富了对同一样点不同模型的误差估计，从而利用基于数据同化方法的多模型协同反演算法 可以更加有效地结合不同模型之间的优点，进而提高反演精度.

表 3 多模型协同反演叶绿素a浓度结果统计分析Table 3 Statistical result of multi-model retrieval of Chlorophyll a
2.3 多模型协同反演结果不确定性估计

对反演结果不确定性的估计，不仅可以评价模型的好坏，同时还可以为数据同化提供准确的误差估计. 反演结果的不确定性估计通常采用以下方法：使用线性逼近或线性回归的方法计算置信区间，或者使用Levenberg-Marquardt方法进行最小二乘优化，以协方差矩阵对角线元素的平方根表示对应反演值的标准偏差[28]. 本研究中，采用Bates等[29]提出的最优化方法，计算逐点的置信区间，为每个验证点提供质量估计. 将该方法应用于多遥感影像的多模型协同反演，则可以获得每个像元的误差估计，从而可以获取叶绿素a浓度反演误差的时间和空间分布情况. 置信区间(ci)的计算方法如下：

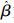其中，x0为验证点叶绿素a浓度，为回归系数，s为模型均方根误差，t(N-P； α/2)是自由度为N-P，置信度为α/2的T分布.

针对验证数据，逐点计算置信度为95%的置信区间(图 4)，对比发现，随着参与多模型协同反演的模型个数的增加，区间长度逐渐减小. 这就说明，随着参与多模型协同反演的模型个数的增加，同化结果的精度也随之提升. 与之前的统计结果(表 3)相吻合. 同时对于每个验证点，笔者以6模型(6个模型参与多模型协同反演)为例，将多模型协同反演值结合置信区间与真值进行对比(图 5). 通过对比发现，大部分验证点位的真值都落在了以多模型反演值为中心的置信区间内. 说明利用置信区间，可以有效地估计产品的不确定性，同时可以有效地针对每个验证点位独立地估计反演值误差，从而可以估算太湖叶绿素a浓度估计的误差分布情况.

图 4 不同模型针对验证数据的置信区间长度的对比Fig. 4 Comparison of the length of confidence interval between different models

图 5 6模型反演结果的不确定性估计Fig. 5 Uncertainties evaluation for retrieval results of six models
3 结论

(1)基于数据同化方法的多模型协同反演算法，通过对多模型反演结果的有效加权，可以有效地融合不同模型的优点，改善单模型反演精度较低区域反演结果，从而整体提高了反演精度. 有利于水环境质量监测和评价.

(2)目前，该方法利用实测水体高光谱遥感反射率数据融合了不同模型的反演结果. 该方法的成功实现依托于不同模型的差异性和对模型误差的准确估计. 同化产品质量的不确定性估计使得获取叶绿素a浓度的误差空间分布图成为可能，同时也可以获取反演产品的误差估计，从而为进一步的数据分析提供可能.

(3)将该方法应用于其他水质参数如：总磷、 总氮、 悬浮颗粒物等的反演研究中，可以对水环境更加全面、 综合的评价.

(4)通过对该方法的学习研究，可以为融合多遥感影像的反演结果提供一定的理论基础.

参考文献
[1] 马荣华, 唐军武, 段洪涛, 等. 湖泊水色遥感研究进展[J]. 湖泊科学, 2009, 21 (2): 143-158.
[2] 黄昌春, 李云梅, 徐良将, 等. 内陆水体叶绿素反演模型普适性及其影响因素研究[J]. 环境科学, 2013, 34 (2): 525-531.
[3] Morel A Y, Gordon H R. Report of the working group of water color[J]. Boundary Layer Meteorology, 1980, 18 (3): 343-355.
[4] 李素菊, 吴倩, 王学军, 等. 巢湖浮游植物叶绿素含量与反射光谱特征的关系[J]. 湖泊科学, 2002, 14 (3): 230-233.
[5] 杨煜. 基于HJ-1高光谱数据的巢湖叶绿素a浓度三波长因子反演模型研究[D]. 南京: 南京师范大学, 2010.
[6] 李云梅, 黄家柱, 韦玉春, 等. 用分析模型方法反演水体叶绿素的浓度[J]. 遥感学报, 2006, 10 (2): 169-175.
[7] Li Y M, Wang Q, Wu C Q, et al. Estimation of Chlorophyll a concentration using NIR/Red bands of MERIS and classification procedure in inland turbid water[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50 (3): 988-997.
[8] 施坤, 李云梅, 刘忠华, 等. 基于不同光谱主导因子的内陆湖泊水体叶绿素浓度三波段反演模型研究[J]. 环境科学, 2010, 31 (12): 2873-2881.
[9] Moradkhani H, Sorooshian S, Gupta H V, et al. Dual state-parameter estimation of hydrological models using ensemble Kalman filter[J]. Advances in Water Resources, 2005, 28 (2): 135-147.
[10] McLaughlin D. An integrated approach to hydrologic data assimilation: interpolation, smoothing, and filtering[J]. Advances in Water Resources, 2002, 25 (8-12): 1275-1286.
[11] Gu J, Li X, Huang C L, et al. A simplified data assimilation method for reconstructing time-series MODIS NDVI data[J]. Advances in Space Research, 2009, 44 (4): 501-509.
[12] 黄春林, 李新. 基于集合卡尔曼滤波的土壤水分同化实验[J]. 高原气象, 2006, 25 (4): 665-671.
[13] 赵骞, 田纪伟, 曹丛华, 等. 渤海、黄海、东海冬季海流场温度场数值模拟和同化技术[J]. 海洋学报, 2005, 27 (1): 1-6.
[14] Losa S N, Kivman G A, Ryabchenko V A. Weak constraint parameter estimation for a simple ocean ecosystem model: what can we learn about the model and data?[J]. Journal of Marine Systems, 2004, 45 (1-2): 1-20.
[15] 秦伯强, 胡维平, 陈伟民, 等. 太湖水环境演化过程与机理[M]. 北京: 科学出版社, 2004.
[16] Le C F, Li Y M, Zha Y, et al. Specific absorption coefficient and the phytoplankton package effect in Lake Taihu, China[J]. Hydrobiologia, 2009, 619 (1): 27-37.
[17] Jiao H B, Zha Y, Li Y M, et al. Estimation of Chlorophyll a concentration in Lake Tai, China using in situ hyperspectral data[J]. International Journal of Remote Sensing, 2006, 27 (19): 4267-4276.
[18] Yacobi Y Z, Moses W J, Kaganovsky S, et al. NIR-red reflectance-based algorithms for chlorophyll-a estimation in mesotrophic inland and coastal waters: Lake Kinneret case study[J]. Water Research, 2011, 45 (7): 2428-2436.
[19] Gurlin D, Gitelson A A, Moses W J. Remote estimation of chl-a concentration in turbid productive waters - Return to a simple two-band NIR-red model?[J]. Remote Sensing of Environment, 2011, 115 (12): 3479-3490.
[20] DallOlmo G, Gitelson A A, Rundquist D C. Towards a unified approach for remote estimation of chlorophyll-a in both terrestrial vegetation and turbid productive waters[J]. Geophysical Research Letters, 2003, 30 (18): 1-4.
[21] Gitelson A A, Schalles J F, Hladik C M. Remote chlorophyll-a retrieval in turbid, productive estuaries: Cheapeake Bay case study[J]. Remote Sensing of Environment, 2007, 109 (4): 464-472.
[22] Gitelson A A, DallOlmo G, Moses W, et al. A simple semi-analytical model for remote estimation of Chlorophyll a in turbid waters: Validation[J]. Remote Sensing of Environment, 2008, 112 (9): 3582-3593.
[23] Le C F, Li Y M, Zha Y, et al. A four-band semi-analytical model for estimation chlorophyll a in highly turbid waters: the case study of Taihu Lake, China[J]. Remote Sensing of Environment, 2009, 113 (6): 1175-1182.
[24] 周琳, 马荣华, 段洪涛, 等. 浑浊Ⅱ类水体叶绿素a浓度遥感反演(Ⅰ): 模型的选择[J]. 红外与毫米波学报, 2011, 30 (6): 531-536.
[25] DallOlmo G, Gitelson A A. Effect of bio-optical parameter variability on the remote estimation of chlorophyll a concentration in turbid productive waters: experimental results[J]. Applied Optics, 2005, 44 (3): 412-422.
[26] 周冠华, 柳钦火, 马荣华, 等. 基于半分析模型的波段最优化组合反演混浊太湖水体叶绿素a[J]. 湖泊科学, 2008, 20 (2): 153-159.
[27] 徐京萍, 张柏, 宋开山, 等. 基于半分析模型的新庙泡叶绿素a浓度反演研究[J]. 红外与毫米波学报, 2008, 27 (3): 197-201.
[28] Press W H, Teukolsky S A, Vettering W T, et al. Numerical recipes in C: The art of scientific computing[M]. (2nd ed.). Cambridge: Cambridge University Press, 1992.
[29] Bates D M, Watts D G. Nonlinear regression analysis and its applications[M]. New York: John Wiley, 1988.